Kriging與改進一次二階矩融合的可靠性分析方法*

袁修開,孔沖沖,顧 健

(廈門大學 航空航天學院， 福建 廈門 361005)

在結構可靠性分析中，失效概率的求解方法可分為三類：近似解析法、數字模擬法、代理模型方法[1]。近似解析方法包括改進一次二階矩(Advanced First Order Second Moment, AFOSM)[1-2]、均值一次二階矩(Mean Value First Order Second Moment, MVFOSM)和R-F法[3]等。近似解析方法計算量少，但是在處理復雜非線性問題時，其精度難以保證。數值模擬法包括蒙特卡洛仿真(Monte Carlo Simulation， MCS)[4]、線抽樣(Line Sampling, LS)[5-6]法、重要抽樣(Importance Sampling, IS)[7]和子集模擬(Subset Simulation, SS)[8-9]等。該類方法為了保證計算精度，需調用結構功能函數的計算次數較多，計算代價大，且在處理包含有限元模型的隱式極限狀態問題時，計算效率低下，是影響該類方法應用的重要因素。代理模型方法包括響應面法[7-11]、神經網絡法[12-13]、支持向量機法(Support Vector Machine, SVM)[14-16]等。該類方法專門針對隱式極限狀態問題，能夠顯著提高分析效率，因而在工程中得到廣泛應用，其中Kriging方法作為一種典型的連續插值迭代方法，以其精確的插值技術備受人們的關注[17]。本文著眼于采用該技術來進一步提高改進一次二階矩方法的分析效率和適用范圍。

改進一次二階矩法通過將非線性功能函數線性展開，然后用線性功能函數的失效概率來近似原非線性功能函數的失效概率[1]。和均值一次二階矩法相比，AFOSM在設計點(Most Probable Point, MPP)處而非均值點處將功能函數線性化，提高了分析計算的精度。呂震宙等[1]對改進一次二階矩的理論介紹和推導過程做了詳細的描述。改進一次二階矩亦在眾多工程領域得到了廣泛的應用，比如：葛耀君等[18]在橋梁顫振可靠性評估中，使用改進一次二階矩方法計算了小失效概率條件下的可靠度；侯曉亮等[19]在評價軟土基坑支護設計中的抗隆起穩定性時，采用改進的一次二階矩可靠度計算方法評價基坑抗隆起穩定性；鄭財等[20]在研究三軸數控機床的運行誤差時，用改進一次二階矩法對其可靠性及靈敏度進行了分析計算；曾照輝等[21]在研究動力渦輪工作時的可靠性時，采用參數化建模通過混合模擬(有限元、響應面、改進一次二階矩法三者結合)的方法對其進行可靠性分析等。改進一次二階矩針對變量維數小，非線性程度不大的小失效概率問題來說，具有很高的計算效率和良好的分析效果。然而在改進一次二階矩中求解“設計點”，及其包含的偏導數的計算是難點，目前常用的方法為有限差分法，但是其對于隱式極限狀態函數(需有限元分析)，有限差分的步長很難確定，且增加了功能函數的計算次數，增大了計算量、效率低。

Kriging代理模型不僅具有良好的擬合效果和局部估計的特點，而且具有較好的連續性和可導性，故具有廣泛的應用前景。韓忠華[22]在Kriging模型及代理優化算法研究進展中，對Kriging方法的背景、意義、理論以及發展現狀做了詳細的描述；聶雪媛等[23]在研究飛行器結構剛度氣動優化設計中采用Kriging方法建立代理模型，該方法能夠處理復雜目標的全局優化問題；黃曉旭等[24]提出一種將Kriging模型與子集模擬方法結合的可靠性分析方法用于解決小失效概率的工程結構問題；陳立立等[25]采用Kriging代理模型進一步驗證自由變形技術在RAE2822翼型優化設計中的應用；韓少強等[26]提出了一種將梯度信息與Kriging模型構建相結合的方法用于氣動反設計研究。

基于改進一次二階矩的實用性及Kriging模型的效率和良好的可導性，本文提出一種Kriging與改進一次二階矩融合的可靠性分析方法。所提方法在改進一次二階矩迭代計算設計點的過程中借助Kriging模型計算迭代點的偏導數值，并將迭代過程中的迭代點用于更新Kriging模型，兩者有機融合來求解失效概率。最后通過結合數值算例與工程算例驗證該方法的可行性和高效性。

1 Kriging方法

(1)

其中：F(β,x)為線性回歸模型；z(x)為一隨機過程；f(x)=[f1(x),f2(x),…,fp(x)]Τ(p為基函數的數目)為輸入向量x的多項式基函數，提供模擬的全局近似[29]；β=[β1,β2,…,βp]Τ為回歸系數列向量。

函數z(x)為高斯隨機過程[30]，作為局部近似[29]，其均值為0，方差為σ2，協方差滿足下式的特征：

Cov[z(x(i)),z(x(j))]=σ2R(γ,x(i),x(j))

(2)

式中：γ=[γ1,γ2,…,γn]為一個相關函數中參數向量；x(i),x(j)是試驗樣本X中任意兩個樣本點；R(γ,x(i),x(j))為相關函數，相應類型有高斯函數、指數函數、冪函數、樣條函數等[31-33]。這里采用常用的高斯相關函數，其數學表達式為：

(3)

當獲得樣本輸入X={x(1),…,x(N0)}(N0為初始樣本量)和輸出Y={y(1),…,y(N0)}后,可以計算得到式(1)中的回歸系數向量β*和式(2)中過程方差σ2[32]：

β*=(FTR-1F)FΤR-1Y

(4)

(5)

相關函數中的參數向量可以通過極大似然估計得到：

(6)

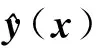
(7)

式中，r(x)=[R(γ,x(1),x),…,R(γ,x(N0),x)]T為輸入量x與已知樣本點X的相關函數，r*可以通過計算Rr*=Y-Fβ*得到。對于Kriging模型的詳細理論分析可以參照文獻[32-33]。

Kriging模型對輸入量和響應量的關系可達到較高的擬合精度，且在工程中已經得到了廣泛的應用[23-26]。

2 基于Kriging方法與改進一次二階矩的融合方法

所提方法采用Kriging方法高效計算偏導數，用于進一步提高改進一次二階矩的效率。由于Kriging模型中的回歸函數和相關函數都是簡單的函數體，在模型建立好后，即可簡便計算出相應的偏導數，因此可將之用于改進一次二階矩的求解過程中。同時，由于一般情況下樣本量越多，Kriging模型構建越精確。為了充分利用已有信息，所提方法將改進一次二階矩求解進程中的近似設計點信息運用于Kriging模型的更新構建中，提高Kriging模型的精度，進而將Kriging方法與改進一次二階矩有機融合。

步驟1：構建Kriging模型。

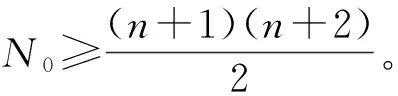
采用蒙特卡洛法隨機抽取N0樣本點X={x(1),x(2),…,x(N0)}(含均值點)，代入結構功能函數中計算響應值Y={y(1),…,y(N0)}，然后根據樣本點構建初始的Kriging模型。

當回歸模型采用一階多項式，則輸入向量x的基函數向量為f(x)=[1,x]，隨機過程采用高斯過程，如式(3)所示，由第1節式(4)可知樣本量、回歸模型、隨機過程確定后，便得到回歸系數向量β*和r*，于是得到極限狀態函數g(x)初始的Kriging代理模型

(8)

步驟2：將Kriging導數信息運用于AFOSM。

在原有改進一次二階矩方法中，對原極限狀態函數在設計點x*處線性化：

(9)

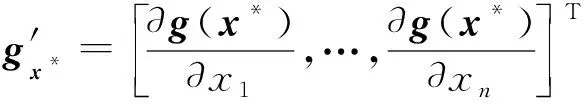
一般采用迭代的算法來獲得[1]設計點，即設置初始設計點值，如設為均值點x*(0)=μ，而后在迭代過程中逐步對設計點值進行更新。此外，在計算導數的時候，需要較多的計算代價，尤其是在變量維數較多的情形下。在本文所提方法中，采用構建的Kriging代理模型來獲取近似導數信息，進一步提升AFOSM的效率。即運用式(8)所示的代理模型計算導數

(10)

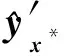
(11)

由此，在后續改進一次二階的迭代求解過程中，導數的計算完全由構建的Kriging模型來計算。

步驟3：更新Kriging模型及設計點直至收斂。

將迭代過程中的中間迭代點添加到構建初始Kriging代理模型的樣本點中，對前面建立的Kriging代理模型進行更新和修正，提高Kriging模型的精度，從而提供更為準確的導數信息，為所提融合方法的最終收斂提供保障。做法如下：

重復將步驟2中得到的設計點值應用到步驟1中，更新Kriging模型的迭代過程，直到前后兩次的可靠度指標的相對誤差滿足設定的精度要求為止，最后對應的可靠度指標ψ和失效概率Pf為：

(12)

Pf=Φ(-ψ)

(13)

本文所提方法的流程圖如圖1所示。

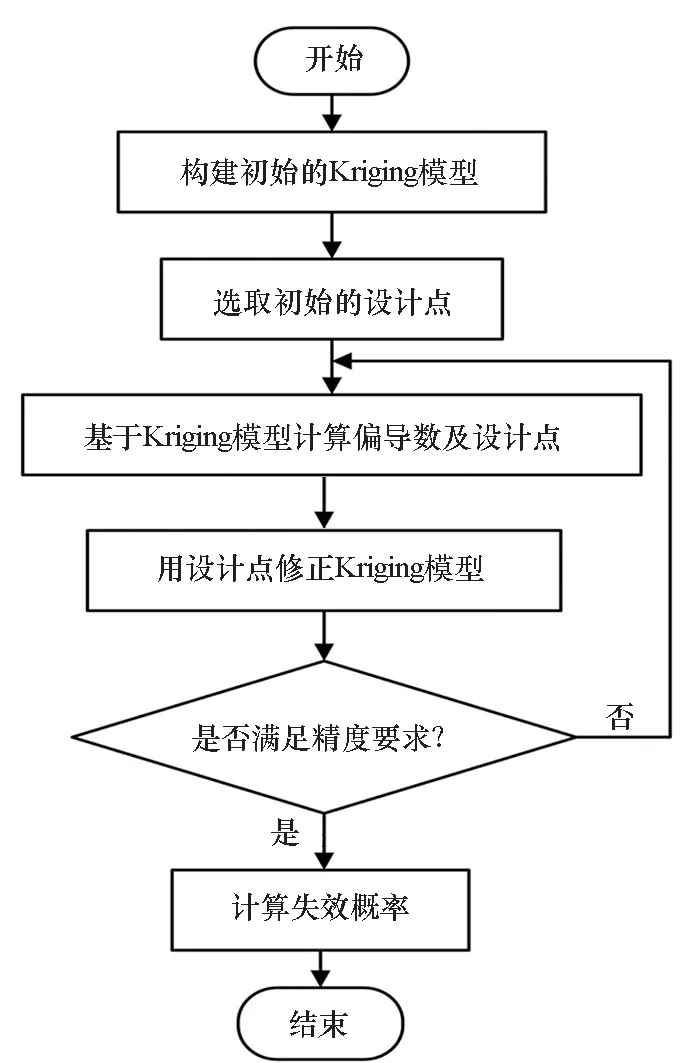
圖1 Kriging與改進一次二階矩融合方法流程圖Fig.1 Flow chart of Kriging and AFOSM

3 算例分析

為了驗證所提方法的適用性，該節結合數值算例和屏蔽閘閥結構的工程算例進行說明。采用本文所提融合方法對各例進行可靠性分析，并與其他分析方法進行比較，包括：AFOSM，即常規改進一次二階矩方法[1]；Kriging+MCS，即建立足夠精度的Kriging模型后再使用MCS方法[28]；MCS，即直接使用蒙特卡洛法。

本文以MCS直接方法計算的值作為精確值(通過大樣本數來計算得到)，以AFOSM 和Kriging+MCS兩種方法來與本文方法進行對比。需要指出的是，對于可靠性計算效率的評定，一般通過極限狀態的計算(調用)次數來衡量。本文構建Kriging模型所采用的樣本點是通過計算極限狀態函數得到，所以樣本點數也表示了極限狀態函數的計算次數。為了考察本文所提方法中初始Kriging模型構建的隨機性，采用不同數目的樣本點構建初始Kriging模型，然后進行可靠性分析。在以下三個算例中用本文方法1和本文方法2表示不同樣本點下本文所提方法計算效果。

算例1非線性極限狀態函數g1(x)為：

g1(x)=x1-x2x3

(14)

其中：變量x1,x2,x3均服從正態分布，其分布信息分別為x1～N(7000,14002)，x2～N(187 500,28 1252)，x3～N(0.024,0.001 442)。

首先驗證用Kriging方法計算改進一次二階矩偏導數的可行性。本文方法采用蒙特卡洛隨機抽取5個樣本點和均值點組成的初始樣本點構建初始Kriging模型，由構建的Kriging模型計算第一次迭代點即均值處偏導數信息，同時使用AFOSM中有限差分(其步長為0.001)計算偏導數，以下算例與此相同，計算結果如表1所示。

從表1可以看出，在均值點處，根據初始Kriging方法得到的偏導數與理論計算出來的偏導數的相對誤差在3%以內，已具有足夠的精度。

采用本文方法及其他方法進行可靠性分析的結果如表2所示。以MCS方法的結果(視作精確值)作為參照，各方法的失效概率與精確值都比較接近，誤差均小于1%。從計算效率上講，AFOSM計算極限狀態函數26次，Kriging+MCS方法中使用200個樣本點構建了Kriging代理模型，而后用蒙特卡洛抽樣方法計算失效概率。本文方法收斂準則為|ψi-ψi+1|/ψi≤5%，以下兩個算例中設計點的確定方法相同。本文方法1使用6個初始樣本點構建初始Kriging模型，經過兩次迭代修正便可計算出極限狀態函數的失效概率，計算次數為6+2。為了檢驗方法穩健性，使用不同的初始樣本點進行分析，亦列在表中，記為本文方法2，計算次數為4+2。表2中本文方法1和本文方法2計算結果一致，與MCS計算結果在誤差允許范圍內，由此可以看出本文所提方法的效率和適用性。

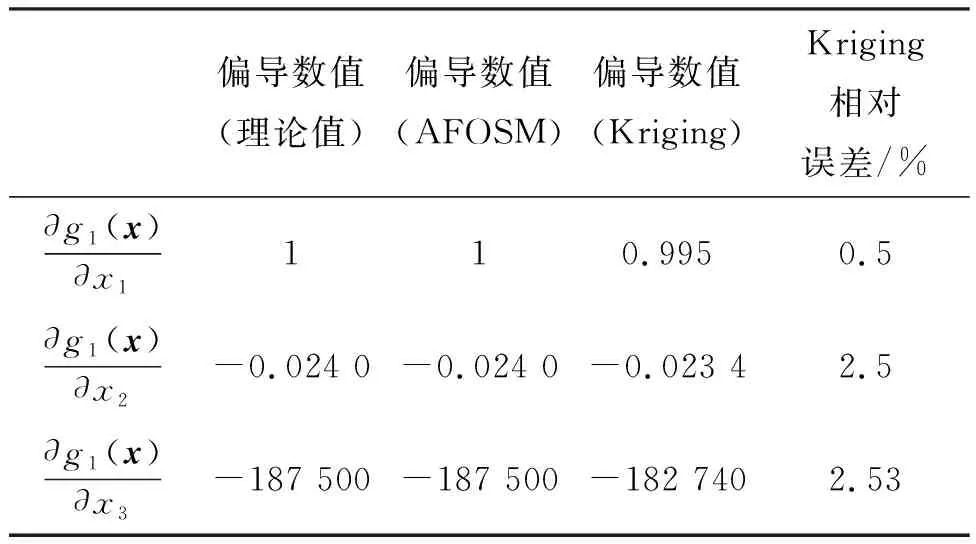
表1 初始Kriging模型計算極限狀態函數的偏導數(均值點)Tab.1 Partial derivative of the limit state function by the initial Kriging model (at the mean point)

注：?g1/?xi為極限狀態函數對變量的偏導數值。

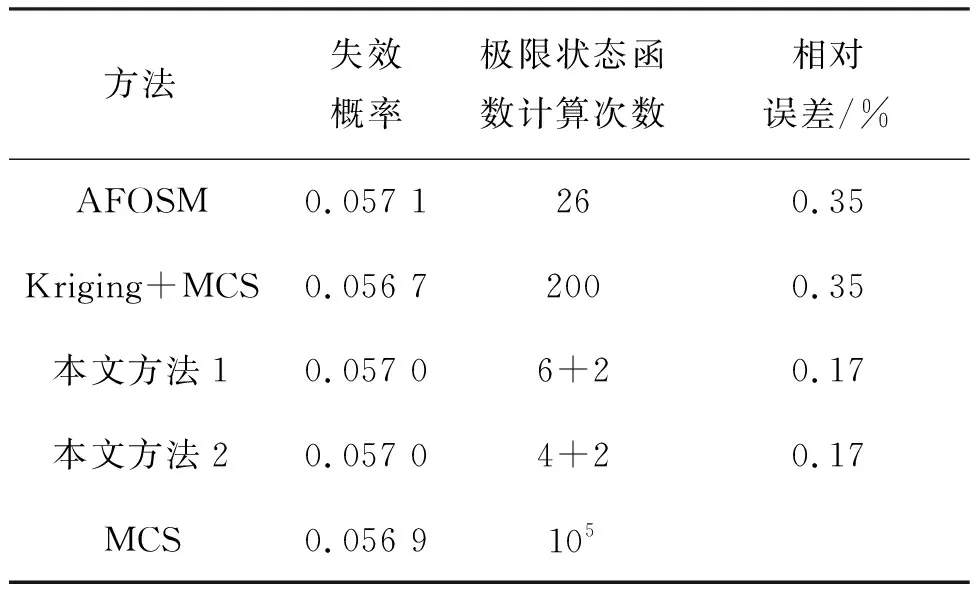
表2 算例1不同方法得到的可靠性分析結果Tab.2 Reliability analysis results obtained by different methods in example 1

算例2非線性極限狀態函數g2(x)為：

(15)

其中：基本隨機變量x1,x2,x3,x4均服從正態分布，分別為x1～N(83.5,0.122)，x2～N(83.5,0.122)，x3～N(83.5,0.122)，x4～N(150,0.252)。

采用本文融合方法計算均值點處的偏導數值如表3所示，可靠性分析結果如表4所示。

從表3可以看出，在均值點處，根據初始Kriging方法得到的偏導數與理論計算出來的偏導數值相對誤差在7%以內，與算例1相比相對誤差值偏大，原因是極限狀態函數的非線性提高，隨機變量的維度增多。

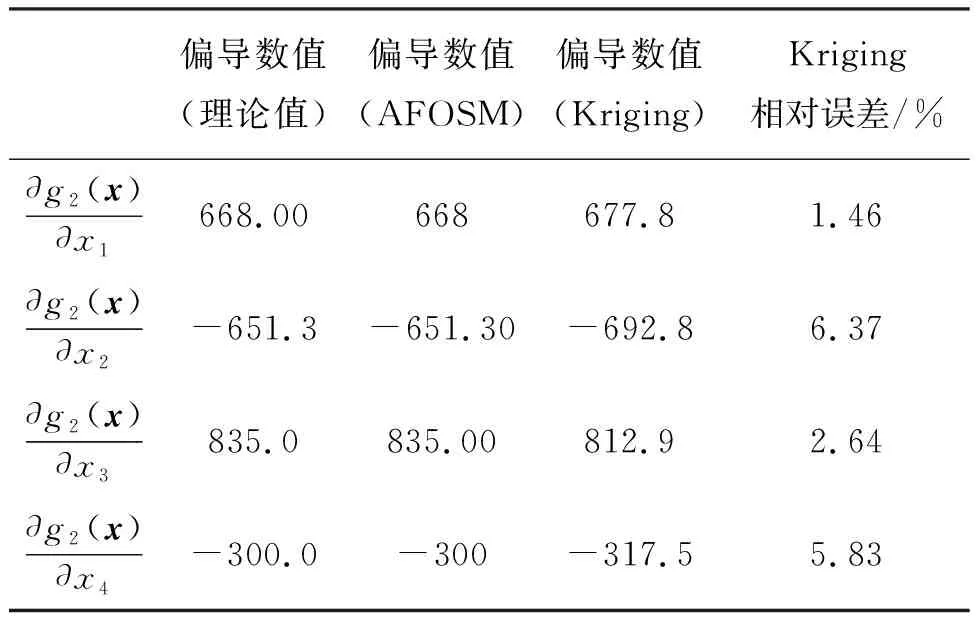
表3 基于初始Kriging模型計算極限狀態函數的偏導數(均值點)Tab.3 Partial derivative of the limit state function by the initial Kriging model (at the mean point)

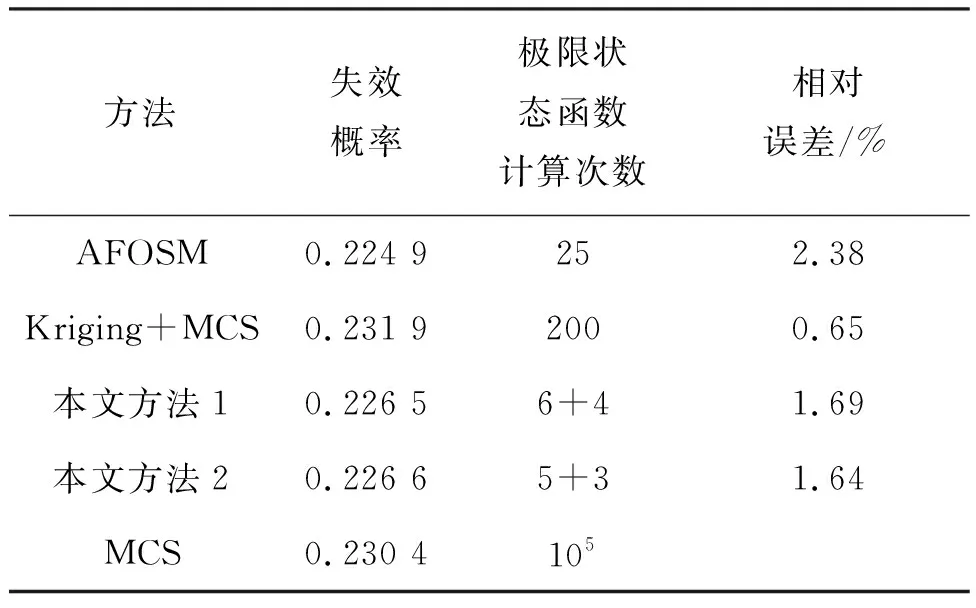
表4 算例2不同方法得到的可靠性分析結果Tab.4 Reliability analysis results obtained by different methods in example 2

同樣從表4可以看出，以MCS方法的結果(視作精確值)作為參照，其他三種方法的失效概率與精確值都比較接近，但是從計算極限狀態函數的次數來說，對于常規改進一次二階矩調用次數最多為25次，Kriging+MCS方法采用200個樣本構建Kriging模型。而本文方法采用不同的初始樣本數來進行分析，結果亦列在表中本文方法1和本文方法2。可以看出本文方法計算次數最少，效率最高。

算例3閘板可靠性分析一屏蔽閘閥的結構如圖2所示，建立相應的有限元來分析接觸面(閘板與密封座)最大應力值。該結構的相關參數有：閘板的傾斜角θ，材料彈性模型E，閘板與密封座的摩擦系數f，閘板上端的均布載荷p。假定各參數均服從正態分布，分布參數為θ～N(5，0.12)，p～N(140,102)，E～N(197 000,10002)，f～N(0.24,0.012)。以結構的最大應力不超過給定極限應力，建立結構的極限狀態函數，即

g(θ,E,f,p)=[σ]-σmax

(16)

其中：[σ]=310 MPa為極限應力；σmax為結構中閥板和密封座接觸面的最大應力值可以表達為：

σmax=ANSYS(θ,E,f,p)

(17)

其中，ANSYS(θ,E,f,p)表示由調用ANSYS有限元分析得到。

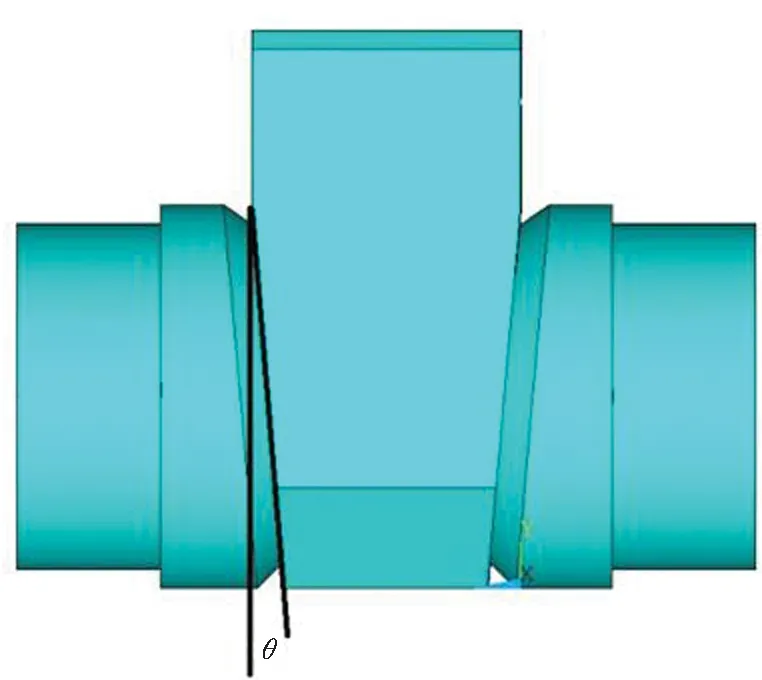
(a) 正視圖(a) Front view

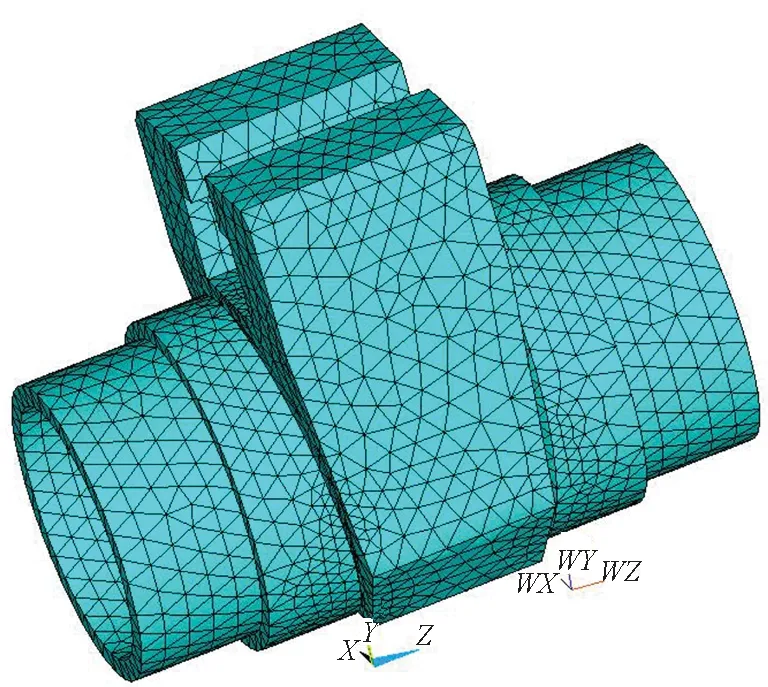
(b) 有限元網格劃分(b) Finite element meshing圖2 屏蔽閘閥結構的三維有限元模型Fig.2 The three-dimension finite element model of shielded gate valve structure

表5給出了各方法的計算結果。可以看出，對于隱式函數，常規的AFOSM方法無法計算結構的失效概率，從側面也反映了本文所提方法的優勢。Kriging+MCS使用300個樣本點構建了Kriging代理模型，然后通過MCS計算失效概率。本文方法計算兩次，一次調用6+6次結構極限狀態函數，另一次調用5+4次，計算得到的失效概率值相近。同樣從該例可看出本文所提方法的效率和對解決工程結構問題的適用性。

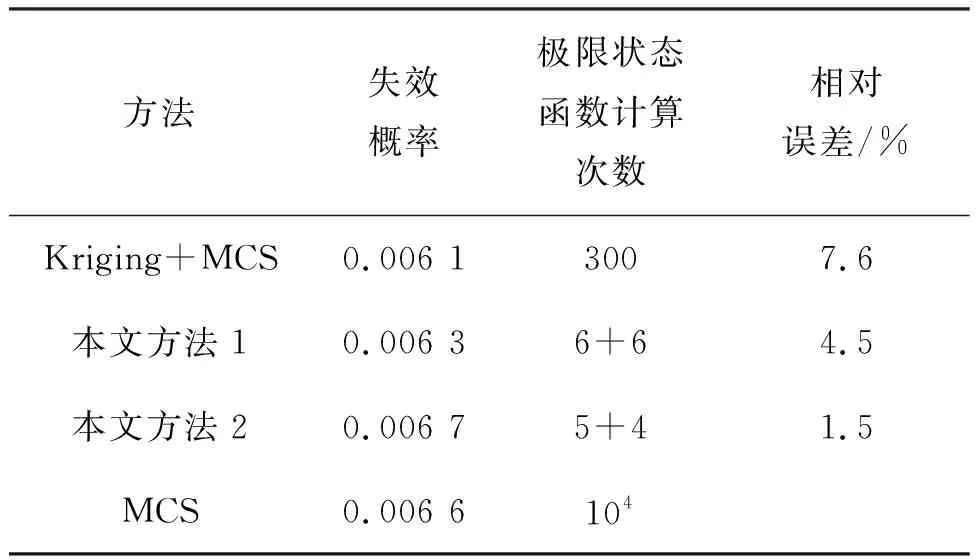
表5 屏蔽閘閥的可靠性分析結果Tab.5 Reliability analysis results of shielded gate valves

4 結論

本文提出了將Kriging方法和改進一次二階相融合的可靠性分析方法。該方法針對AFOSM在處理復雜非線性函數或包含有限元分析的隱式極限狀態函數的可靠性問題時，采用Kriging方法求解極限狀態函數的偏導數，為AFSOM迭代計算設計點時提供偏導數信息，同時將AFSOM迭代產生的中間迭代點用于更新Kriging模型進一步提高偏導數的計算精度。

通過兩個數值算例可以看出，所提方法中運用Kriging得到求解梯度信息與理論計算的基本一致。最終計算的結果亦能滿足精度要求，而在效率上與傳統的AFSOM相比有了進一步的提升。所提方法拓寬了AFOSM使用的范圍，可以用于解決復雜的工程可靠性問題，且提高了其求解效率。