船用鍋爐汽包水位內模滑模控制

段蒙蒙,甘輝兵

(大連海事大學 輪機工程學院， 遼寧 大連 116026)

大型油船的燃油輔鍋爐是產生高溫高壓蒸汽的裝置，具有蒸發量大和蒸汽壓力高等特點，可為船用設備提供熱能和動力。[1]鍋爐汽包水位是鍋爐裝置中的一個重要運行參數，對其進行控制是保證鍋爐安全運行的必要條件。對于非線性時滯、強耦合和非自平衡的鍋爐汽包水位系統來說，傳統的比例-積分-微分(Proportional Integral Differential,PID)控制由于參數固定，對系統的所有工況不能表現出良好的控制性能。Smith預估控制雖然能補償系統延時的影響，但對建模誤差比較敏感，而內模控制作為Smith預估控制的延伸，對系統建模誤差具有一定的魯棒性，但當模型誤差較大時，系統有可能不穩定，甚至發散。滑模控制作為一種魯棒控制，對系統的不確定性和外界干擾具有強魯棒性，文獻[2]和文獻[3]采用預測控制原理，將滑模控制與預測控制相結合，得到多模型滑模預測控制策略，取得了良好的控制效果，但計算量較大。文獻[4]和文獻[5]將內模控制結構與滑模控制律相結合對一階時滯系統進行控制，內模控制結構補償了時滯對系統的影響，積分滑模面設計的滑模控制律提高了系統的控制精度和魯棒性，仿真結果達到了預期的控制效果。但傳統的積分滑模控制(Integral Sliding Mode Control, ISMC)不具有全程魯棒性，且在系統初始誤差較大時，尤其是在執行器飽和的情況下，積分作用會惡化系統的暫態性能，對于具有內模控制結構的不穩定系統在階躍擾動后，也會產生穩態誤差，甚至使系統發散。

針對汽包水位的非自平衡和非線性時滯特性，將內模控制結構與滑模控制律相結合，提出基于全程非線性積分滑模面與擾動補償的內模滑模控制策略，不僅能消除滑動模態的趨近階段，使系統具有全程魯棒性，而且能很好地抑制擾動和消除穩態誤差。

1 鍋爐汽包水位內模控制方案

目前的鍋爐汽包水位主要采用三沖量串級PID控制，雖然其結構簡單、參數易整定，但其只適用于定工況，而內模控制是基于被控對象模型的新型控制器，具有設計簡單、跟蹤性能好和魯棒性強等優點。[6]在鍋爐汽包水位內模控制中，將內環PID控制與鍋爐水位系統的傳遞函數組合形成汽包水位的廣義被控對象。鍋爐汽包水位的內模控制結構見圖1。

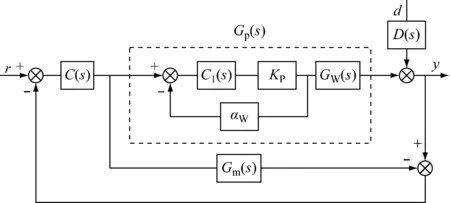
圖1 鍋爐汽包水位的內模控制結構

圖1中:C1為內環PID控制;KP為調節閥;αW為給水流量反饋裝置;GW為鍋爐水位系統傳遞函數;Gp為廣義被控制對象;Gm為被控對象的過程數學模型;D為擾動通道的傳遞函數;C為內模控制器。由圖1可得系統的輸入輸出關系為

(1)

當模型匹配，即Gm(s)=Gp(s)，可將式(1)簡化為

y(s)=C(s)Gp(s)r(s)+

(1-C(s)Gm(s))D(s)ds

(2)

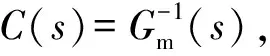
(3)

由式(3)可知：內模控制可克服系統外界擾動，并能很好地跟蹤輸入信號。內模控制器的設計為

1) 將過程模型分解為最小相位部分和非最小相位部分，即

Gm(s)=Gm+(s)Gm-(s)

(4)

2) 對最小相位系統求逆，并與適當階次的濾波器聯立構造內模控制器，即

(5)

Ⅰ型、Ⅱ型濾波器的典型形式分別為

(6)

(7)

式(6)和式(7)中：λ為濾波時間常數;n0為濾波器的階次，使控制器物理可實現。

2 基于全程非線性積分滑模面與擾動補償的鍋爐汽包水位內模滑模控制

2.1 鍋爐汽包水位內模滑模控制結構設計

汽包水位內模滑模控制器結構見圖2。本文采用Smith預估結構補償時滯對系統造成的影響，控制器采用滑模控制律增強系統在不同工況下的魯棒性。控制方案包括2個控制器：Q為基于滑模控制律的主控制器;Gd為基于擾動補償的擾動抑制控制器。em為模型誤差，ym-為模型的預測輸出。

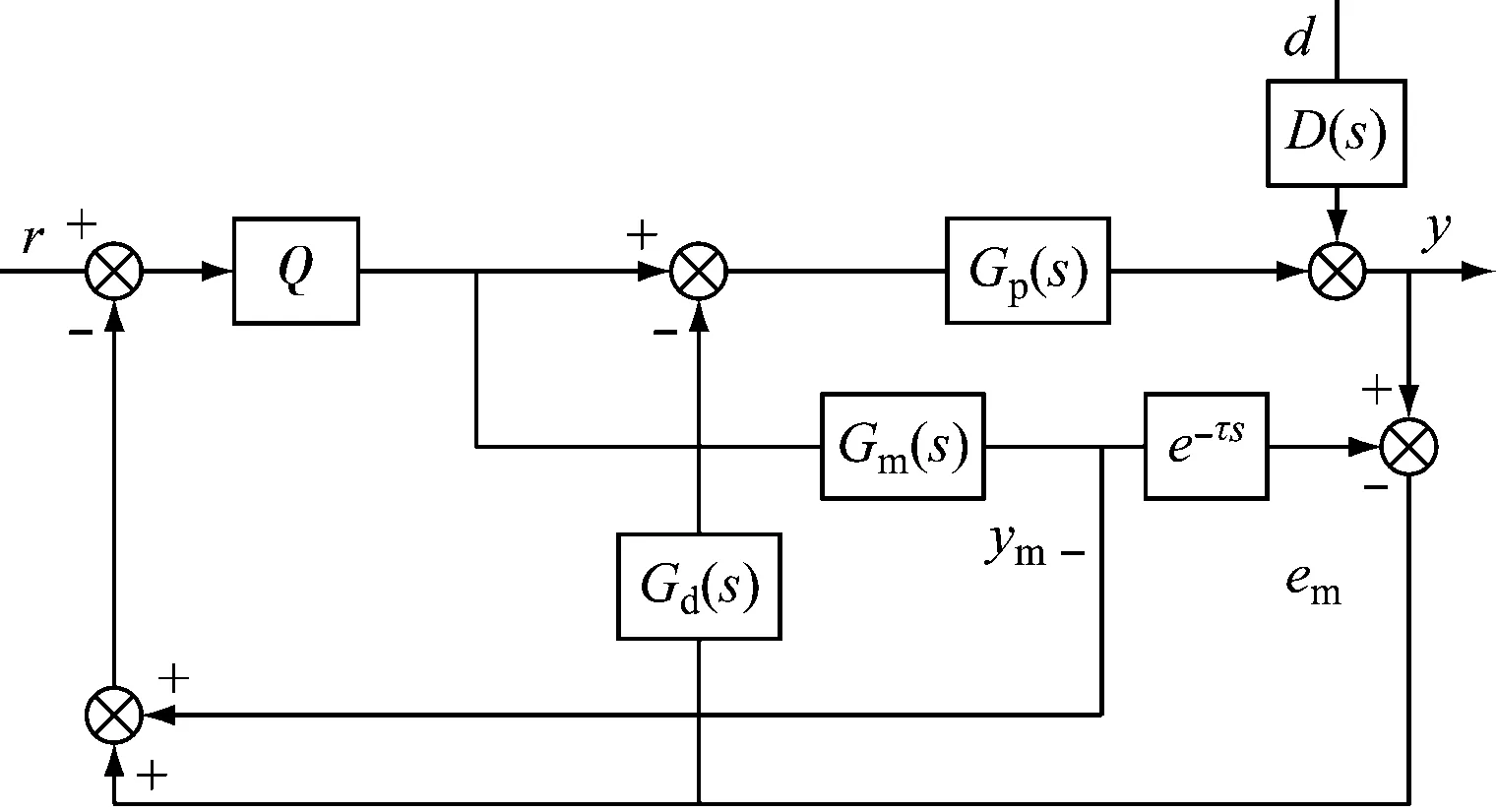
圖2 汽包水位內模滑模控制結構

在鍋爐汽包水位的控制系統中，若把內回路近似看作比例環節，則鍋爐水位系統的廣義傳遞函數為

(8)

則

(9)

Gm+=e-τs

(10)

假設系統的設定值為r,則跟蹤誤差為e=r-y=r-ym--em。在滑模控制中，傳統的積分滑模面為

(11)

式(11)中：n為系統的階次。由于積分作用會惡化系統的暫態性能，而滑模控制的優點在于系統狀態處于滑動模態時才具有魯棒性。因此，考慮設計全程非線性積分滑模面改善系統的暫態性能，消除滑模控制系統的到達階段，使其在初始時刻就處在滑模面上。設計鍋爐汽包水位控制系統的全程非線性積分滑模面為

(12)

為分析非線性飽和函數g(e)[7]的特性，引入勢能函數為

(13)

對式(13)進行求導，可得

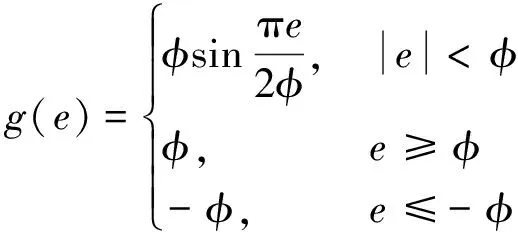
(14)

非線性函數G(e)與g(e)的曲線圖見圖3。

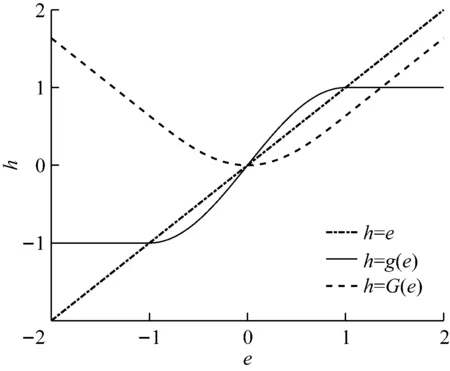
圖3 非線性函數G(e)和g(e)的曲線圖

由圖3可知:設計的非線性函數g(e)具有“小誤差放大，大誤差飽和”的特點，通過選擇不同的參數φ獲得期望的誤差狀態。

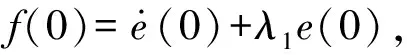
(15)

考慮到理想情況下em=0,由式(15)可得

λ2g(e)+f(0)ke-kt

(16)

由式(9)可得

(17)

聯立式(16)與式(17),求解得到

(18)

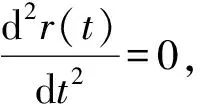
(19)

為減少滑模控制中的抖動，設計自適應積分切換控制律[9]為

ud=Kw(|ρ|+η)sgn(s)

(20)

(21)

符號函數sgn(s)可由飽和函數sat(s)代替，有

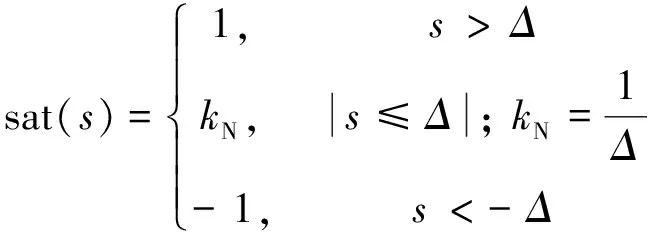
(22)

式(20)～式(22)中:Kw>0;Kf<0。在滑動模態時，若s及其積分值趨近于零，則切換增益也趨近于零，從而消除抖振。當系統離滑動模態較遠時，由于積分的累積作用導致切換增益較大，會增加系統的抖振。因此:引入負權值Kf，可有效避免切換增益不斷增大，減小抖振;η為很小的一個正數，能使系統在接近滑模面時具有一定的收斂速度。滑模控制器中總的控制量為u=uc+ud。為分析系統的穩定性，選擇的Lyapunov方程為

(23)

s(λ2g(e)+f(0)ke-kt)

(24)

將式(17)、式(19)和式(20)代入式(24)得

(25)

式(25)顯然滿足滑模到達條件，系統能進入滑動模態。

2.2 擾動抑制控制器設計

擾動控制器Gd的主要控制目標是鎮定不穩定的被控對象并提高外界干擾的抑制能力。本文采用直接合成法對Gd進行設計。當系統模型匹配(即廣義被控對象)Gp=Gm時，系統的擾動與輸出之間的關系可根據圖2表示為

(26)

從式(26)中可觀察到包含時滯的特征方程，因此基于不穩定二階系統加上時間延時對擾動控制器進行設計。控制器的結構考慮具有滯后超前補償的PID控制器[10]為

(27)

式(26)中包含Gd的特征方程為

1+GdGm-e-τs=0

(28)

系統的時間延遲采用一階Pade近似，將式(27)和式(9)代入式(28)得

(29)

將式(29)中α的值設定為0.5τ，式(29)分解簡化為

d4s4+d3s3+d2s2+d1s+1=0

(30)

由式(29)和式(30)得

(31)

根據直接合成法，式(30)理想的方程式為

(λs+1)4=0

(32)

將式(32)與式(30)和式(31)相比較，可解得kp、ki、kd、α、β的值分別為

(33)

(34)

(35)

α=0.5τ

(36)

(37)

式(33)～式(37)中：λ為系統的性能調節參數，λ越小，其標稱性能越好，λ越大，其魯棒性能越好。為使擾動控制器不影響系統整體的魯棒性，其值應取相對較大。

3 仿真試驗結果分析

依據圖2建立鍋爐汽包水位的MATLAB/Simulink仿真模型，采用設計的內模滑模控制策略進行仿真驗證。在鍋爐汽包水位系統中，αW=0.084,Kp=20，鍋爐水位系統傳遞函數為

(38)

系統的廣義被控對象和擾動通道的傳遞函數分別為

(39)

(40)

在滑模控制律中取λ1=0.15，λ2=0.005，k=0.300，Kw=301.5，Kf=-1,Δ=0.2,φ=0.01；擾動抑制控制器中取λ=18，則α=2.5，β=4.523 6，η=0.01，kp=0.312 8，ki=3.858 9×10-4，kd=5.851 0。在鍋爐汽包水位控制中，對基于內模控制結構的傳統積分滑模控制律(Internal Model Control Structure with Integral Sliding Mode Control Law, IM-ISMC)與全程非線性積分滑模控制律(Internal Model Control Structure with Global Non-Linear Integral Sliding Mode Control Law,IM-GNISMC)進行仿真，設計工況和+20%參數變化且模型匹配時系統輸出和控制器輸出的曲線分別見圖4～圖7，2種控制方法的控制效果對比見表1。

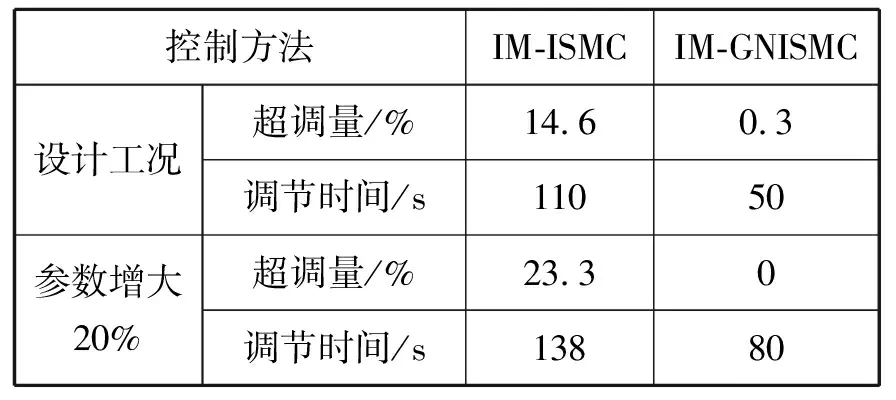
表1 IM-ISMC與IM-GNISMC控制效果對比

由表1和圖4～圖7可知：在設計工況下，由于初始誤差較大，積分作用增強，使得IM-ISMC控制器輸出較大，系統超調量為14.6%，過渡時間為110 s；IM-GNISMC控制器輸出平穩，系統輸出基本無超調,系統調節時間為50 s。當系統參數變化+20%且模型匹配時，IM-ISMC控制器使系統超調增大23.3%，過渡時間延長至138 s，這是由于初始階段系統狀態不處在滑模面上，在趨近階段不具有魯棒性，控制器輸出跳變嚴重，無法實際應用；IM-GNISMC控制器輸出平順，系統調節時間為80 s,參數攝動對系統的性能幾乎沒有影響，控制系統具有全程魯棒性和良好的跟蹤性能。

對提出的內模滑模控制方案與鍋爐汽包水位三沖量串級PID控制和內模控制進行仿真試驗，以說明其具有良好的控制性能。

模型匹配時系統有無擾動控制器的響應曲線見圖8。由圖8可知:當系統存在干擾時，無擾動控制器的內模滑模控制方案使系統存在穩態誤差，而有擾動控制器的內模滑模控制方案抑制干擾，消除穩態誤差。

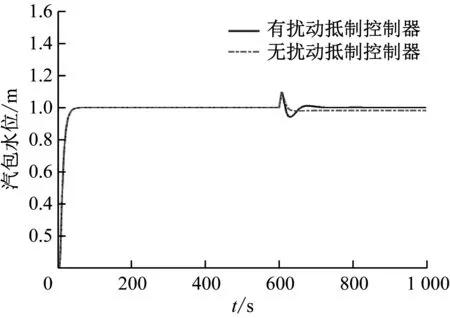
圖8 模型匹配時有無擾動控制器的系統響應

在鍋爐汽包水位控制系統中，上述3種控制方法分別在設計工況、時間常數T增大20%和增益K減小20%的情況下，系統的控制效果對比見表2。

當模型匹配時不同控制器的系統響應曲線見圖9。由圖9可知：在系統初始響應時，PID控制的響應慢，且超調量為46%，穩定時間為400 s；內模控制與提出的內模滑模控制的響應速度都很快，但內模控制穩定時間稍長，由于內模控制器采用Ⅱ型濾波器。因此，系統有39%的超調量，而本文提出的內模滑模控制器僅有0.3%的超調，且系統調節時間最短為50 s。在擾動抑制方面，在600 s將階躍擾動施加給系統蒸汽流量。PID控制的擾動抑制性能最差，系統超調最大，穩定時間長，而內模控制由于只有1臺控制器，系統需在跟蹤響應和擾動抑制之間折中。在設計的內模滑模控制方案中，由于控制策略中特有的內模結構和擾動控制器的存在，使得由蒸汽擾動引起的系統不平衡態在主控制器動作前，擾動抑制控制器會優先施加一個水位調節分量，使系統在虛假水位或船舶晃動時具有較強的干擾抑制能力之后，在主控制器的作用下系統快速達到穩定。

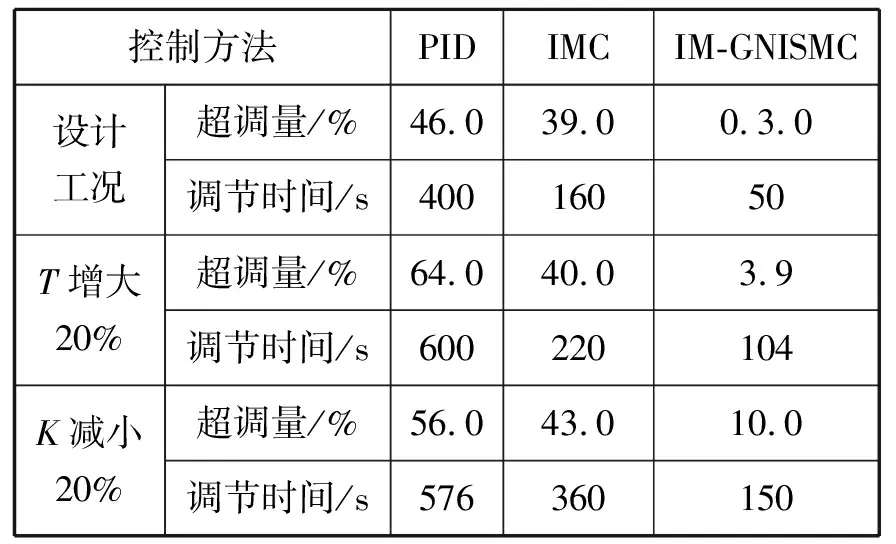
表2 不同控制器作用下汽包水位控制效果對比

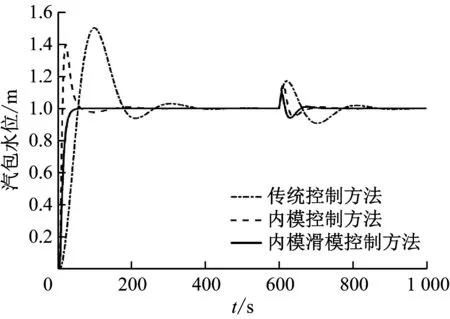
圖9 模型匹配時的3種控制器系統響應

在模型不匹配的情況下，即系統T和K分別增大和減小20%時系統的響應曲線分別見圖10和圖11。在系統初始響應時刻，PID控制與內模控制的超調量更大，穩定時間更長。由表2可知:IM-GNISMC控制器在參數攝動的情況下，系統的超調量和調節時間都十分小。系統的少許超調是由于模型失配導致的，若能準確在線辨識系統被控對象的模型，本文提出的內模滑模控制方案將表現出更好的控制性能。綜上所述，IM-GNISMC控制器在各工況下都有良好的系統跟蹤性能和抗干擾能力，并具有很強的魯棒性。

4 結束語

為進一步提高傳統鍋爐汽包水位控制系統的性能，提出基于全程非線性積分滑模面與擾動補償的內模滑模控制策略，仿真結果表明:本文提出的控制方案不僅可消除時滯對系統的影響，還可提高系統的響應速度，減小系統的超調，增強系統的魯棒性。雖然設計的鍋爐汽包水位的控制方案能取得預期效果，但由于控制模型中的參數較多，有必要進一步對控制器的參數設計進行研究。