基于改進前推回代潮流算法的有源配電網故障定位

潘 翀，劉 鑫

（1.國網四川省電力公司成都供電公司，成都 610064；2.國網四川省電力公司檢修公司，成都 610041）

0 引言

電能是使用范圍最廣泛的能源之一，如何使用可再生能源發電是廣大電力工作者的研究方向，分布式電源技術應運而生。目前，對分布式電源的處理方法是將其接入到當地的配電網中，其發電量也主要采用就地消納的方式，這種有分布式電源接入的配電網也稱為有源配電網。有源配電網中潮流分布的改變意味著和傳統配電網相配對的繼保裝置與基于潮流分布的故障分析算法不再適用。

分布式電源的接入導致配電網的潮流方向發生改變，從故障定位的角度分析有源配電網與傳統配電網的不同之處有：

（1）傳統配電網通過線路換位等方式可以實現三相線路平衡，但當分布式電源接入后，由于饋線的存在使得三相線路不再平衡，整個配電網潮流分布不再呈現平衡性，使用傳統的潮流算法會出現比較大的偏差。

（2）故障情況下故障電流會受到分布式電源類型、接入位置及接地位置等因素的影響，當故障點位于分布式電源后端時，此時的故障電流主要受分布式電源控制。

（3）當電網中出現故障時，分布式電源的參數是未知的，同時接地電阻也具有很大的隨機性，這些對有源配電網中的故障定位都會產生很大的阻礙[1-5]。

配電網的故障定位為實現小區域隔離、避免大范圍停電事故提供了重要參考依據。故障定位可以根據分析過程分為故障區域識別和故障距離定位。故障區域識別指在故障定位過程中首先定位到故障點所在的兩端節點，即故障點所在支路；故障距離定位是指定位故障點在故障支路的位置。

目前，按算法原理劃分，故障定位算法可分為行波法、阻抗法與智能算法3 種。行波法是基于行波在波阻抗不連續點處會發生折反射的原理，通過測量反射行波的傳播時間，再根據行波的速度得到故障點的位置；阻抗法是根據測量故障后的工頻電壓和電流分量，利用配電網的結構信息與線路參數，建立起故障點的距離函數，從而進行故障定位；智能算法主要是根據目前的一些智能算法，采用配電網的結構與線路參數，建立起故障定位模型，來迭代求解故障點的位置[6-10]。

基于上述分析，本文針對有源配電網提出了新的故障定位算法，算法基于最小電流偏差的原理，采用改進的前推回代潮流算法作為故障定位依據，采用遺傳算法作為尋優工具。最后，在改進IEEE 33 節點模型上進行了算法有效性的驗證。

1 最小電流偏差原理

對分布式電源接入的有源配電網在正常運行狀態下的模型如圖1 所示。

為便于分析，假設故障點處采用兩個反向等大的電流源串聯處理，此時該點可看作正常運行情況。當q 點出現故障情況時，該點將會出現接地電流，此時故障情況下的有源配電網模型如圖2 所示。

由疊加定理可知，正常情況時的有源配電網可看作是故障情況時的有源配電網與圖3 所示簡化配電網之和。

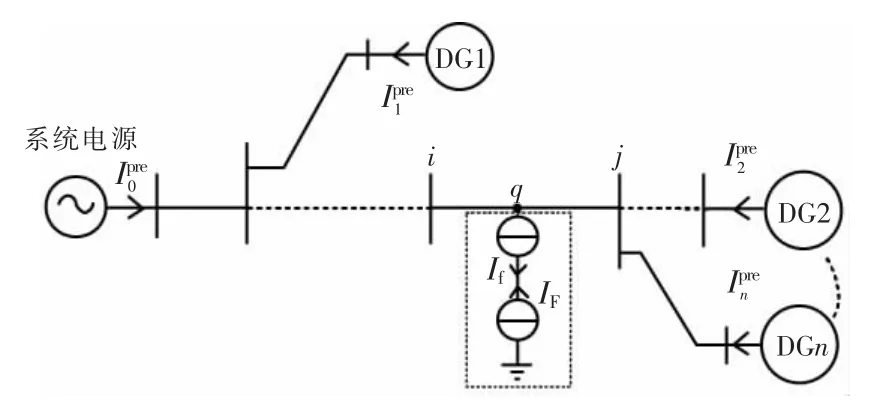
圖1 正常運行的有源配電網模型

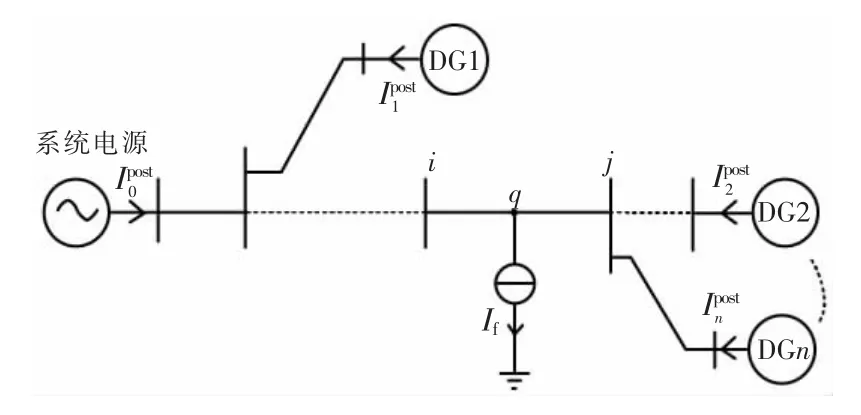
圖2 故障情況下的有源配電網模型

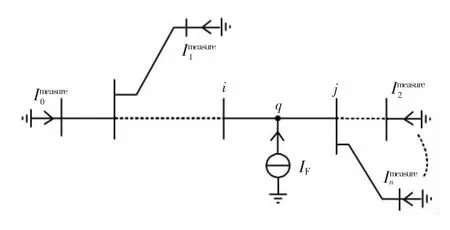
圖3 簡化配電網模型

對簡化配電網模型進行分析可知，此時簡化配電網中的獨立源只有一個位于故障點處的電流源，電流源大小為IF。本文將各個電源出口的電流作為響應值，此時，圖1 中的各電源出口的響應值等于圖2 與圖3 中的響應值疊加，即：

基于上述分析，本文提出的故障定位基本原理就是在簡化網絡中注入電流的方式，求取與Imeasure之間偏差最小的點即為故障點位置（電流偏差最小原理）。在故障定位算法部分，本文采用遺傳算法作為尋優工具，基于電流偏差最小原理來進行故障定位。

2 改進前推回代潮流算法

目前，前推回代潮流算法廣泛應用于配電網潮流計算中，前推回代算法計算速度快，收斂性好，在計算輻射狀配電網結構時具有一定的優勢，前推回代潮流算法主要用于對稱三相計算。本文對有源配電網進行故障定位，在進行潮流計算時需要注意到有源配電網在出現故障時電網結構不再是輻射狀網絡，同時故障情況下電網也不再保持三相對稱，因此，將前推回代潮流算法應用于有源配電網前還需要在算法上做一定的改進。

前推回代潮流計算用于有源配電網潮流計算中，考慮到故障定位時采用的評價函數是基于電流偏差最小，因此，前推回代潮流計算用于求解有源配電網故障定位中求解故障電流的過程可以分為前推與回代兩個過程，具體公式描述如下：

式中： Vn與In分別為配電網中第n 個節點的電流與電壓的三相矢量；其中n+1 節點為n 節點的下游節點；A，B，C，d 分別為網絡的三相阻抗矩陣。

潮流計算過程可簡要描述為： 首先，假設網絡中個節點電壓均為0，通過前推公式對電網進行遍歷，修正各個節點的電流矢量；當完成對整個網絡的電流修正過后，開始進行回代計算，利用修正后的電流值與上一次迭代的電壓值對當前電壓矢量進行修正，一次前推回代過程組成一次算法計算迭代過程。

在進行前推回代潮流計算時，本文采用恒定阻抗模型來代替分布式電源，對于分布式電源的故障電流求解可根據節點電壓求解：

式中： Yn表示分布式電源在故障期間的恒定導納矩陣。

對配電網進行迭代潮流計算時，只有迭代矩陣的譜半徑小于1 才能保證算法的收斂性。當出現接地故障時，迭代矩陣發生改變，會出現譜半徑大于1 的情況，造成潮流計算不收斂的結果[11-17]。

為使得前推回代潮流算法適用于故障情況下的潮流計算，本文的處理方法是在迭代過程中對修正因子作處理。本文在迭代計算過程采用如下的改進方法： 在求解修正量的過程中，增加松弛因子，在上一次的修正量的基礎上求解下一次的修正因子。具體公式表示如下：

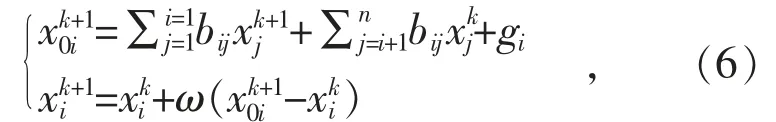
為驗證上述改進方法的有效性及分析松弛因子的選擇，本節在算法驗證中采用改進IEEE 33節點模型做仿真計算，仿真原理如下： 假定支路8-9 的中間位置發生三相接地短路，接地電阻為10 Ω。從而得到迭代計算次數與松弛因子之間的關系曲線如圖4 所示。

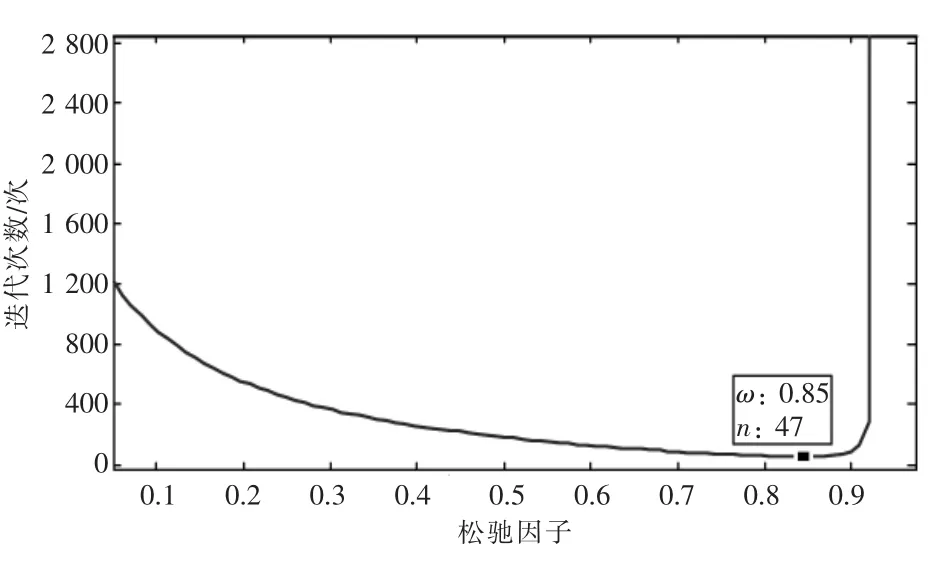
圖4 迭代次數與松弛因子之間關系

由圖4 可知，當松弛因子為1 時，即在不考慮輸入量的情況下，迭代計算結果會出現不收斂的情況；當松弛因子在0～1 之間時，計算結果都呈現了收斂的狀態，這也證明了增加松弛因子的方法可以有效增加算法的收斂性。當松弛因子選擇在0.8～0.9 之間時，通過較少的迭代次數便可以得到相應精度下的迭代結果，但經實驗驗證，松弛因子的選擇與故障位置有關，最好的松弛因子位置大致相同，于是本文選擇松弛因子為0.85作為潮流計算的參數。

綜上所述，具體到本文的算例仿真中，詳細的改進潮流算法流程如圖5 所示。

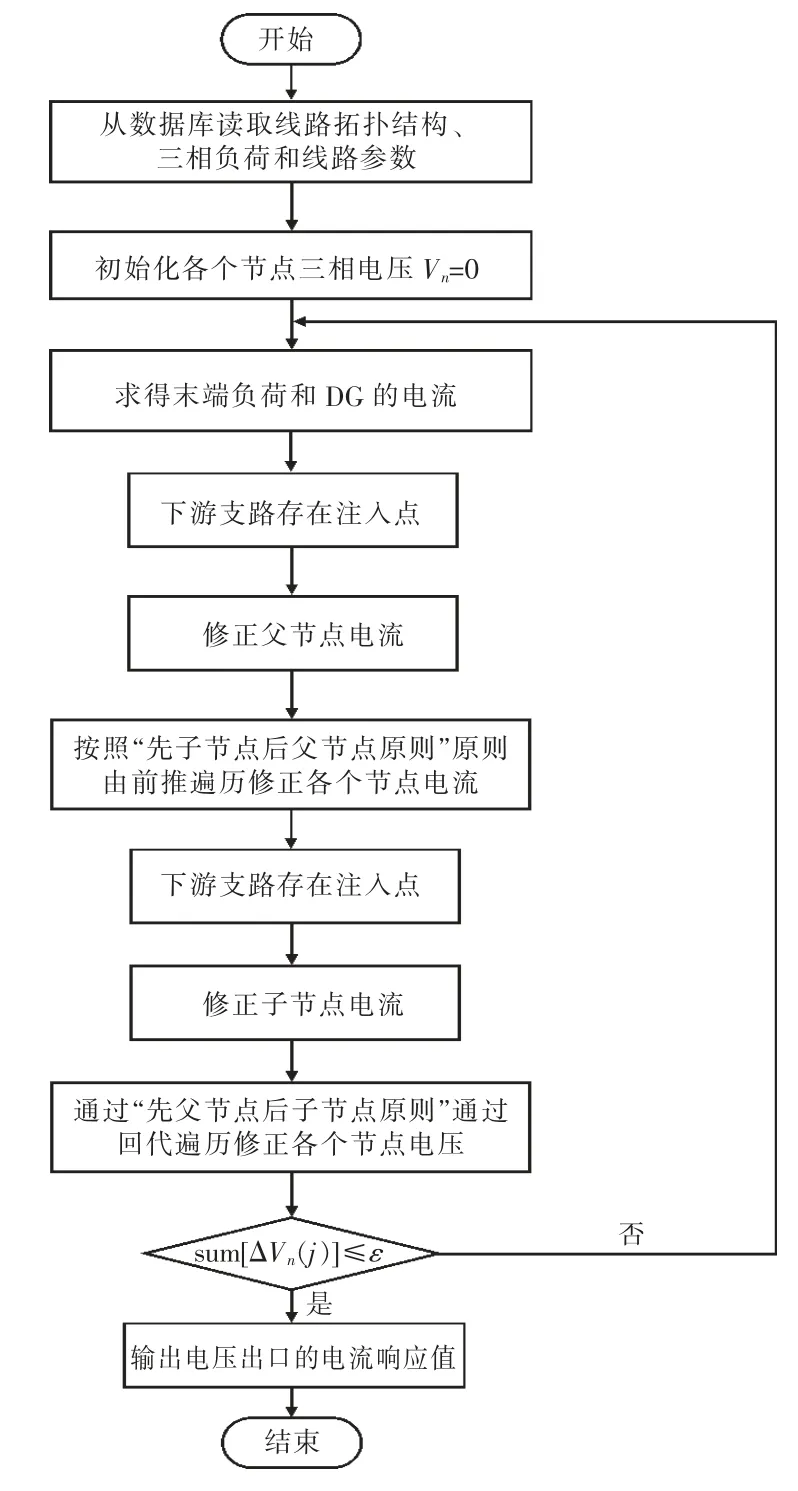
圖5 改進潮流算法流程

3 遺傳算法

遺傳算法是模擬種群在進化過程中將劣質個體淘汰，保留優良個體的過程。通過將整體種群中的個體進行遍歷，保留優秀個體，再將種群進行選擇、交叉與變異等操作得到子代；再從子代中選擇出最優個體，以此類推，直至達到種群迭代次數或者最優個體得到閾值要求。將遺傳算法作為本文故障定位算法，算法原理主要體現在適應度函數的構造上。

適應度函數的構造決定了種群的進化方向，針對具體問題構造適應度函數可以加快迭代過程，增加種群的收斂性，利用fitness 算子進行個體與種群適應度評價，表達式為：

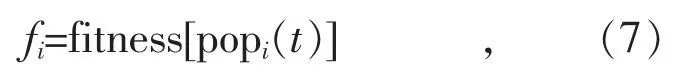
式中： popi（t）表示第i 代種群。

本文采用遺傳算法作為尋優工具，將最小電流偏差作為評價標準，本文構造適應度函數為：

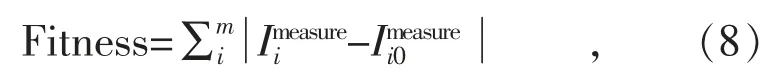
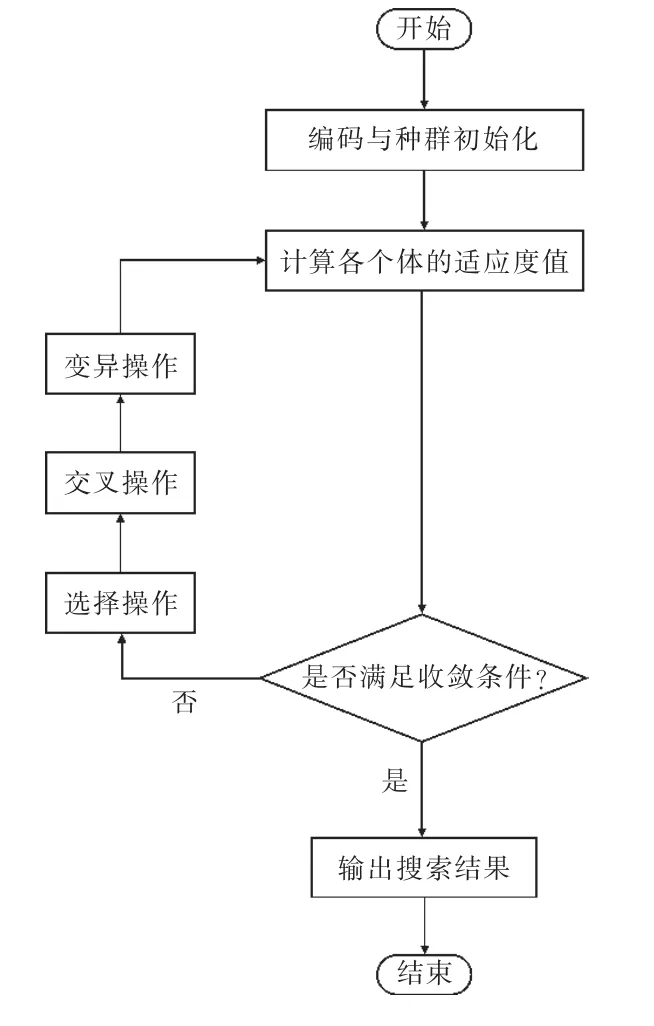
圖6 遺傳算法流程

4 仿真分析

本文采用在IEEE 33 節點配電網模型上改進得到的有源配電網模型，通過在18，22，25 與33 節點處加裝分布式電源，來仿真有源配電網模型，具體網絡模型如圖7 所示。在網絡模型中的不同端位置處設置不同的故障類型與接地電阻來仿真故障情況，利用PSCAD 來獲取暫態電量數據，利用MATLAB 來進行計算分析。

4.1 不同端區域故障分析

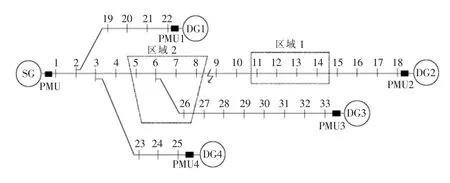
圖7 改進IEEE 33 節點有源配電網模型

配電網呈現輻射狀，在不同的節點處可能存在著很多條分支，本文將所采用的配電網模型根據分支數的不同分為兩端區域與三端區域，分別對應于圖7 中的區域1 與區域2，下面將對這兩個區域進行故障分析。

4.1.1 兩端區域故障分析

對于兩端區域的故障定位仿真，在支路12-13 之間設置單相接地故障，選擇距離12 節點70%處設置故障點，故障電阻為10 Ω。

算法輸出最優個體為：

[0.102 0.699 10.001 12.897]

表示，最優個體的適應度為10.2%；與首端節點之間距離為支路長度的69.9%；故障電阻為10.001 Ω；最后一位表示故障支路末端節點數，采用向上取整的方式，于是確定故障位置處于支路12-13。

4.1.2 三端區域故障分析

對于三端區域的故障定位，與雙端區域分析手段類似，首先在區域2 中選取支路6-26 作為故障點，在與距離首端節點之間相距為支路長度的50%處設置單相接地短路故障，故障電阻為10 Ω，算法輸出種群中的最優個體為：

[0.104 0.498 10.001 25.602]

表明，種群最優個體適應度為10.4%；故障點與首端節點之間的距離為所在支路長度的49.8%；故障電阻為10.001 Ω；所在支路末端節點數為將最后一位向上取整，于是確定故障位置位于節點6-26 之間。

4.2 不同故障類型情況

對于不同的故障類型的分析，選取區域1 作為故障區域，以A 相作為故障相，仿真區域1 內發生單相接地短路、兩相短路、兩相接地短路、三相短路情況，選取故障電阻為10 Ω。給出不同的故障類型在不同的線路上出現故障后，本文算法的定位分析結果如圖8 所示。

圖8 故障類型仿真分析

從圖8 可以看出，在區域1 內發生不同類型的故障時，本文算法均可以得到較好的定位效果，最大定位誤差出現在支路11-12 之間發生的三相短路故障時，最大誤差也在0.45%以下；從整體來看，對配電網中出現最多的單相接地短路故障的定位效果最好。

5 結語

本文提出了有源配電網故障定位算法，基于電流最小偏差原理，對前推回代潮流算法做了改進，使其適用于故障情況下計算。采用改進的IEEE 33 節點模型作為仿真模型，對本文的故障定位算法，分別在雙端區域與三端區域進行了仿真驗證，結果表明在不同端的區域內發生故障時，故障定位都能取得更好的效果；同時，通過在雙端區域內設置不同的故障類型來仿真驗證，表明在不同的故障類型下，算法仍然能夠保持較好的定位精度。