基于多風電相關性場景生成法的配電網隨機多目標無功優化

倪 爽，崔承剛，鄭慶榮，郝慧玲，楊 寧，奚培鋒

（1.上海電力大學，上海 200090；2.國網上海市電力公司，上海 200122；3.上海市智能電網需求響應重點實驗室，上海 200063）

0 引言

隨著高比例風電接入配電網，其出力間歇性和隨機性，疊加多類型負荷波動性，容易造成饋線電壓越限問題，對配電系統優化控制和運行態勢預測分析帶來極大困難[1]。為提高配電網對風電的接納能力，利用OLTC（有載調壓變壓器）、分布式電源、儲能裝置以及并聯電容器、SVG（靜止無功補償器）等各種設備進行無功優化，已成為改善風電接入帶來的問題、提升電能質量的一項重要課題。文獻[2-5]分析了風電接入對配電網的影響，并提出無功功率協調優化控制策略。由于風電具有波動性和不確定性，風功率無法準確預測，上述文獻將風電等不確定性電源的出力視為確定值會對配電網無功優化產生較大誤差[6]，因此需要考慮大規模風電場接入的不確定性[7]。

目前，處理風電不確定性的方法通常有概率解析法和場景生成法。概率分析法一般建模復雜，計算量較大。而場景生成法將含有不確定因素的問題劃分為多個確定的場景進行分析，從而避免了復雜的建模過程[8]。傳統的場景生成法是以風功率歷史數據為基礎，針對某一時間斷面或單一風電場的場景生成。文獻[9]采用Wasserstein距離指標和K-means 聚類場景削減技術生成最優場景；文獻[10]采用結合切片采樣算法的馬爾科夫鏈蒙特卡洛模擬法抽樣生成風電場景；文獻[11]基于單個風電場預測誤差的多元高斯概率密度函數，通過逆變換抽樣技術和場景削減技術生成大量場景。以上文獻均未考慮不同風電場之間的相關性，但當大規模風電并網時，受氣象及風能傳播的影響，多個風電場之間出力必然會顯現出一定的時空相關性，而傳統場景生成法沒有考慮多個風電場出力的時空相關性，具有一定局限性[12]。

針對多風電場的場景生成，文獻[13-16]利用Copula 函數來對多維隨機變量進行建模，將多風電場出力聯合分布函數場景化，建立了場景概率模型。但是這種利用Copula 函數來構建具有相關性的隨機變量概率模型的方法僅能夠描繪2 個風電場之間出力的相關性，并且不能考慮風電場出力的波動性。文獻[17]采用Cholesky 分解排序法描述隨機變量之間的相關性。文獻[18]采用秩相關系數描繪風電與負荷之間的相關性。以上文獻中描述變量相關性的方法計算量較大，且缺乏對生成場景的定量分析。

針對以上問題，本文提出了一種基于多元隨機變量協方差參數辨識的多風電相關性場景生成方法。該方法首先基于風電場功率的歷史數據建立一種非參數的累計經驗分布模型。其次，采用多元隨機變量協方差參數辨識方法，生成風電場功率協方差矩陣，描述不同風電場之間的相關性。再通過逆變換抽樣生成大量符合相關性和波動性特點的多風電場風功率場景，并利用Kmeans 聚類法進行場景削減生成最優場景。接著，以網絡損耗最小、電壓偏移最低為目標函數建立配電網隨機多目標無功優化模型，并采用NSGA-Ⅱ算法求解該模型。最后，本文在改進的IEEE 33 節點進行仿真和分析，通過與傳統的不考慮相關性的場景生成方法進行對比，在波動性貼合度、歷史貼合度以及無功優化效果三個方面進行對比，驗證了該方法的有效性。

1 多風電場相關性模型

1.1 多風電場風功率相關性模型

隨著風電開發力度加大，一個地區的多個風電場在風速統計數據上呈現出一定的相關性，這將會降低含風電的電力系統可靠性。因此在對存在多個風電場接入的系統進行無功優化時，應當考慮不同風電場之間的相關性[19]。

多元風功率模型分為兩類，即多元分布模型[20]和多元時序模型[21]。本文利用協方差矩陣的指數模型構建了風電的多元分布模型，并基于風功率的波動性模型設計了協方差參數辨識的目標函數，用來描述不同風電場功率之間的相關性。

1.2 基于協方差矩陣的多風電場相關性模型

含有相關性的多個風電場的輸出功率可以視為一個多維隨機變量P={Pk，k∈N}。假設多元隨機向量Z=[Z1，Z2，…，Zk]T服從多元正態分布Z～N（μ，∑），K 為風電場個數，期望μ 是K 維零向量，則協方差矩陣∑如式（1）所示：

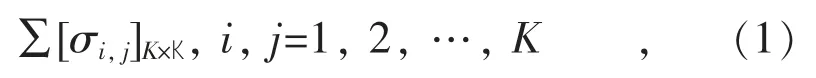
式中： σi，j為隨機變量之間的協方差。

利用指數型的協方差函數對協方差進行建模：

式中： ε 為范圍參數，用于表示不同風電場的隨機變量Zk（k=1，2，…，K）的相關性強度。

估計最佳范圍參數ε 使得隨機生成的風功率場景符合風電的波動性統計規律。為此，本文引入了協方差參數辨識指標Iε[22]：

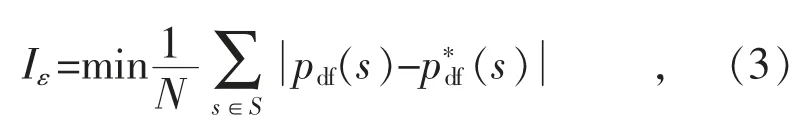
式中： S 為在數值區間[-0.15，0.15]上的等間距抽樣點s 的集合；s 為抽樣點；N 為抽樣規模；pdf（·），（·）分別為動態場景與歷史數據的風功率波動的t location-scale 分布概率密度函數值。

Iε表征了生成的風功率場景的波動與歷史數據的風功率波動的差異性。Iε越小，說明生成的場景越接近歷史數據的概率分布，也就越能準確描述不同風電場功率之間的相關性。

ε 確定以后，協方差矩陣Σ就被唯一確定了，那么就可以產生N 個服從正態分布的多元隨機向量，再進行逆變換抽樣，產生N 個多風電場的風功率場景。

2 多風電場的風功率場景生成方法

2.1 風功率的概率分布模型建立

本文采用一種非參數的經驗分布函數來估計風功率的概率分布[23]，即在風功率的理論分布未知的情況下，將關于風功率隨機變量p 的樣本x1，x2，…，xl按照單調遞增排列，則風功率的ECDF（累積經驗分布函數）可按照式（4）得出：

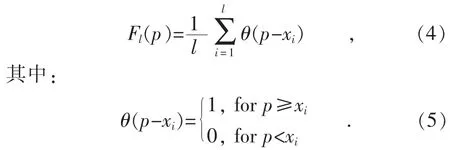
2.2 風功率的逆變換抽樣

根據風功率的累積經驗分布，可通過抽樣法生成風功率場景。常用的抽樣法有拉丁超立方抽樣法、逆變換抽樣法等等。其中逆變換抽樣方法操作簡單，適用于多個存在相關性的風電場輸出功率的場景生成，因此本文選擇逆變換抽樣法生成場景。

假設隨機變量Zk～N（0，1）服從標準正態分布，那么在已知隨機變量Zk的隨機數時，對隨機變量Pk可以采用如下公式抽樣：

逆變換抽樣的示意圖如圖1 所示。

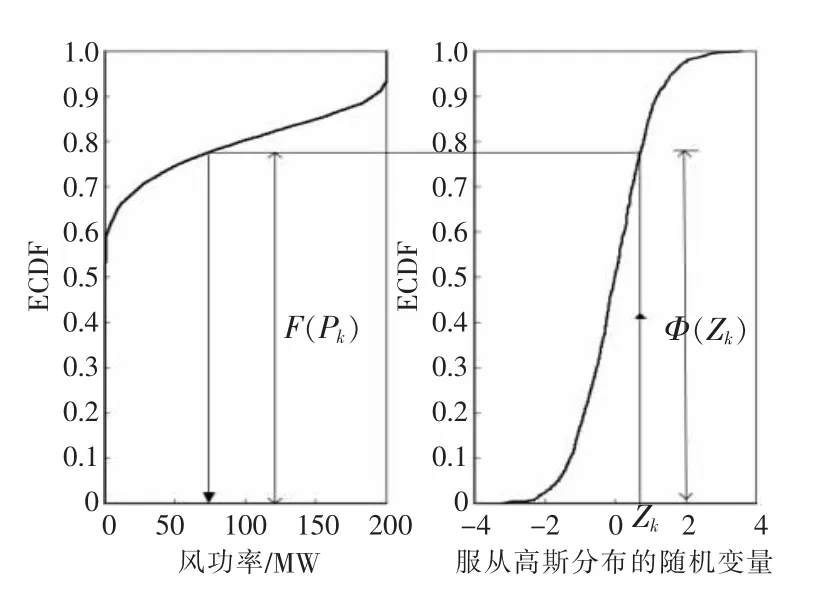
圖1 逆變換抽樣示意圖

2.3 基于多元正態聯合概率分布的多風電場場景生成

綜上，基于多元正態聯合概率分布的多風電場的風功率場景生成步驟如下：

（2）根據各個風電場的歷史數據，計算出各個風電場的風功率波動的歷史數據，并用MATLAB 工具箱中的fitdist 函數確定各個風電場的風功率波動服從的t location-scale 分布。

（3）根據式（3）確定了最佳范圍參數ε 后，再根據式（2）生成對應的協方差矩陣，生成N 個服從正態分布的多元隨機向量，進行逆變換抽樣，產生N 個多風電場的風功率場景。

（4）采用K-means 聚類法[9]將生成的場景削減到M 個具有代表性的場景。

3 基于場景生成的配電網隨機多目標無功優化模型

以網絡損耗的期望最小和節點電壓偏差的期望最小作為目標函數，建立含有多風電場的配電網隨機多目標無功優化模型。

3.1 目標函數

（1）目標一： 網絡損耗

網絡損耗的期望表達式為：

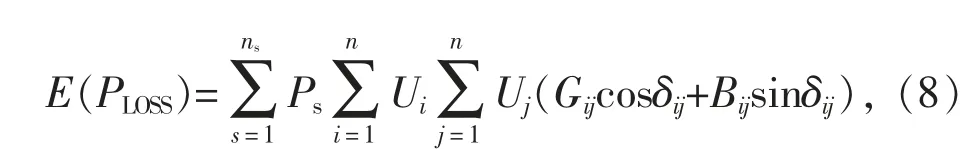
式中： E（）為期望；ns為場景個數；Ps為場景s 對應的場景概率；PLOSS為網絡損耗；n 為系統節點數；Ui為節點i 電壓幅值；Gij，Bij，δij分別為節點i 和節點j 之間的電導、電納、電壓相位差。

（2）目標二： 電壓偏差

古生物學家在整理早期發現的化石時，注意到了那具于19世紀60年代在蒙大拿州出土的化石，發現其特征與腫頭龍相同。這說明其實我們早在150多年前就已經發現了腫頭龍的化石，腫頭龍也成為了北美洲發現最早的恐龍之一。

電壓偏差的期望表達式為：

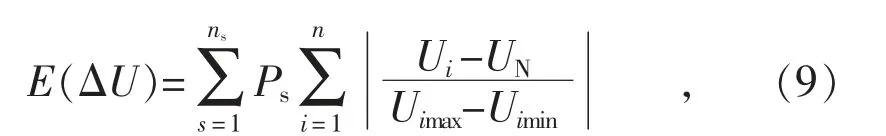
式中： n 為節點總數；Ui為第i 個節點電壓；UN為系統額定電壓；Uimax，Uimin為系統允許電壓的上、下限，分別是1.05UN和0.95UN。

3.2 約束條件

（1）功率平衡約束

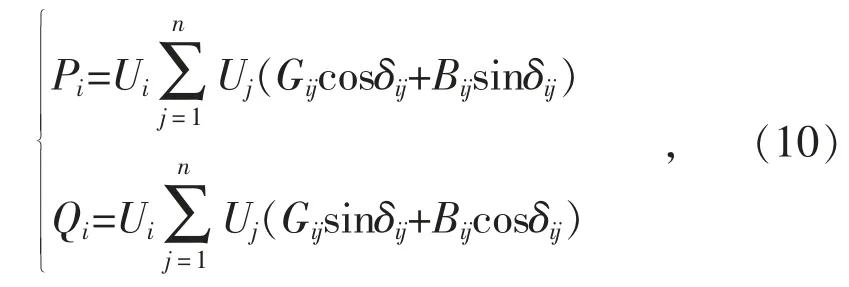
式中： Pi，Qi分別為流進節點i 的有功功率和無功功率；Ui為節點i 電壓幅值大小；Gij，Bij為節點i，j 之間線路導納參數；δij為節點i，j 之間的電壓相位角（超前/滯后）之差。

（2）控制變量約束

控制變量約束主要來自變壓器分接頭檔位T與電容器組的無功補償容量Qc兩個部分，約束關系可表示為：

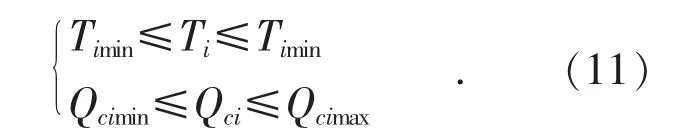
（3）電壓約束

式中： Uimin，Uimax分別為節點電壓幅值允許的下限和上限。

3.3 基于NSGA-Ⅱ算法的多目標優化模型求解

運用NSGA-Ⅱ算法求解配電網隨機多目標無功優化問題最優解的優化流程如圖2 所示。

4 算例分析

4.1 多風電相關性場景生成

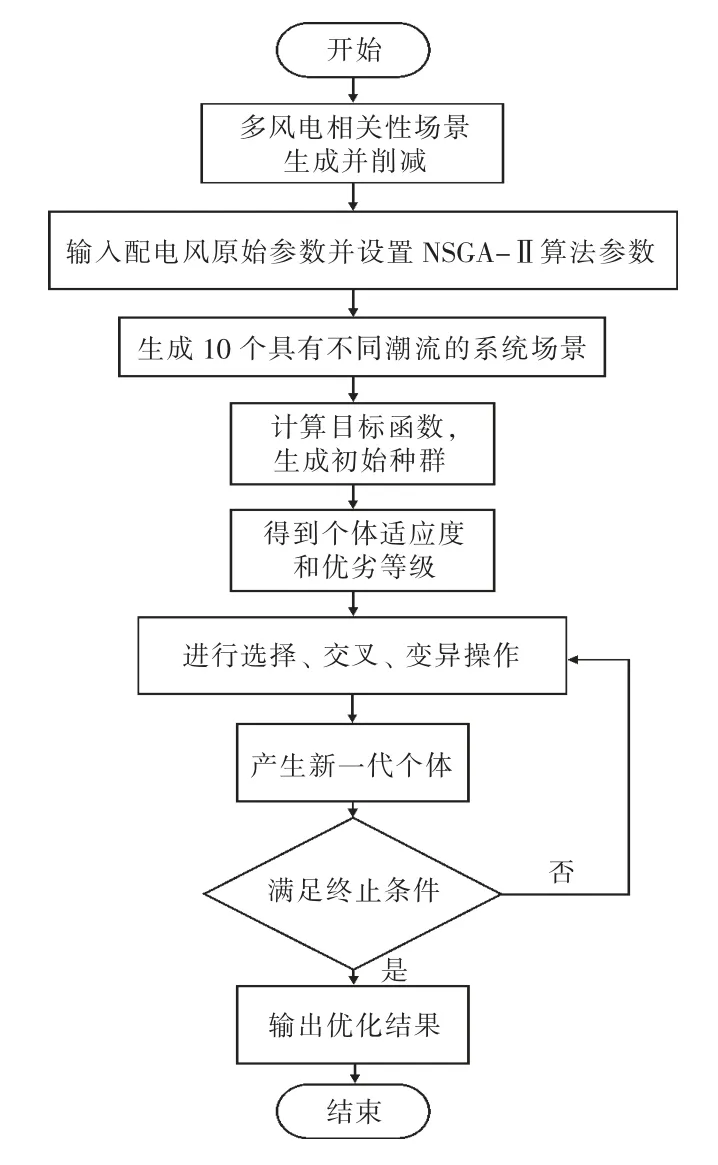
圖2 基于NSGA-Ⅱ算法的無功優化流程

本文采用某地5 個風電場一年內的數據，共計15 120 組，數據采集間隔為5 min，根據本文第2 節提出的多風電場風功率場景生成方法，生成5 個風電場的累積經驗分布如圖3 所示。

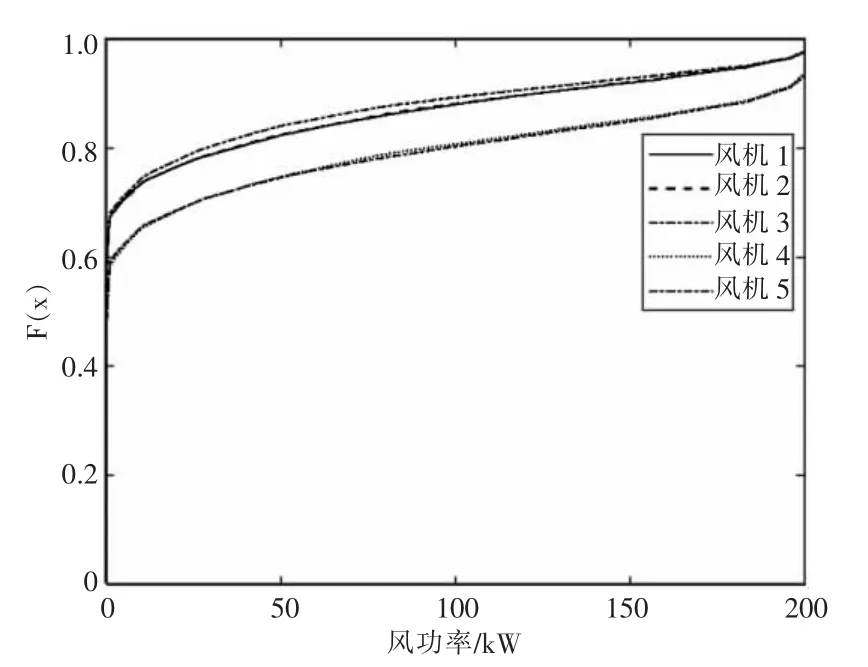
圖3 5 個風電場的累積經驗分布

接著計算確定各風電場的風功率波動服從的t location-scale 分布。本文算例中5 個風電場波動性的t location-scale 分布如圖4 所示，t locationscale 分布參數見附件A。

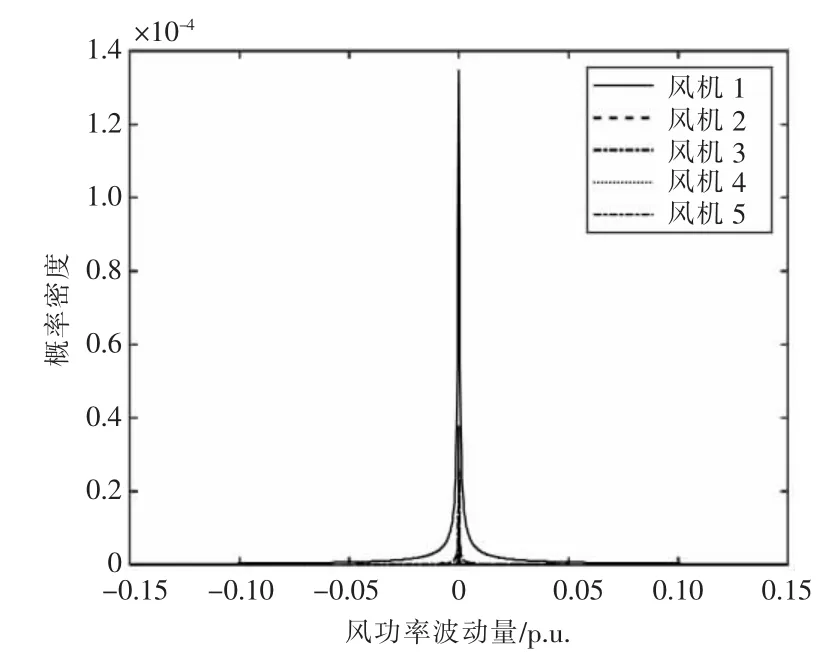
圖4 風功率波動的歷史數據t location-scale 分布

根據式（3），經多次尋優后最終確定本算例最佳值為83，代入式（2）后得到協方差矩陣，生成1 000 個服從正態分布的多元隨機向量。接著進行逆變換抽樣，產生符合5 個風電場相關性的1 000 個風功率場景。最后基于生成的這1 000 個場景，采用K-means 聚類法實現場景削減，最終得到10 個具有代表性的場景。

4.2 場景評估

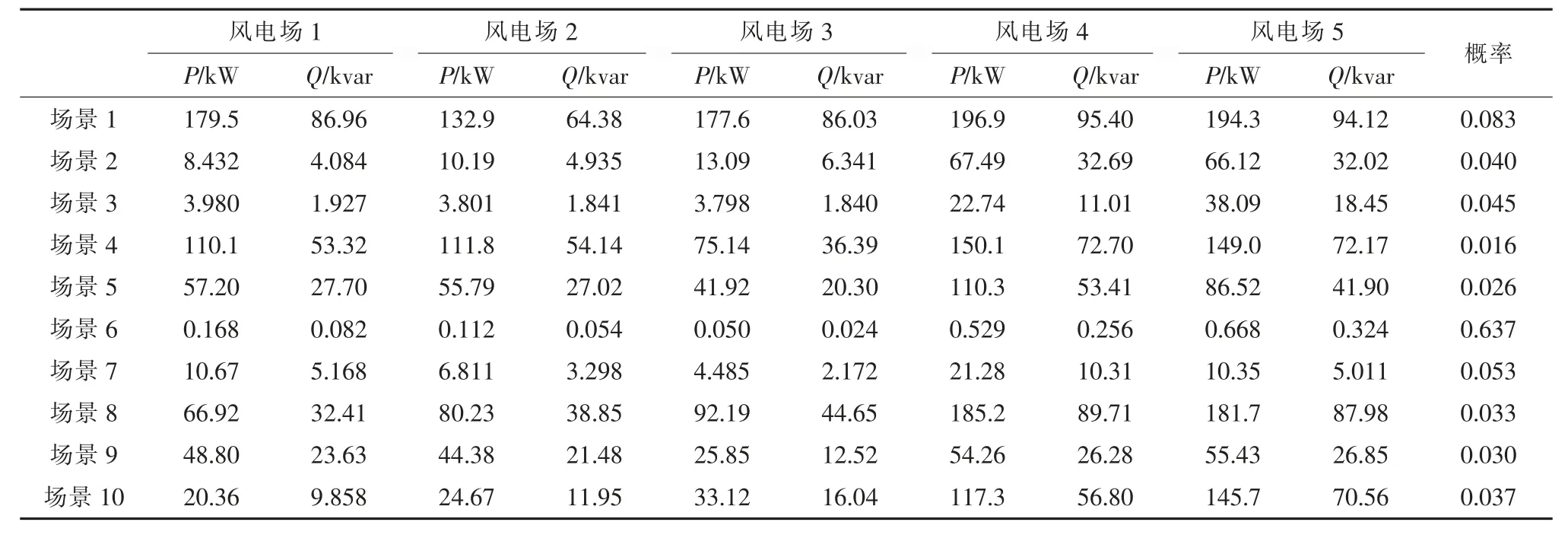
為了便于比較，本文分別用傳統場景生成法和多風電相關性場景生成法來生成場景。2 種方法下最終生成的10 個具有代表性的場景分布分別如圖5、圖6 所示。場景數據及其概率見附錄B中的表B1 和表B2。

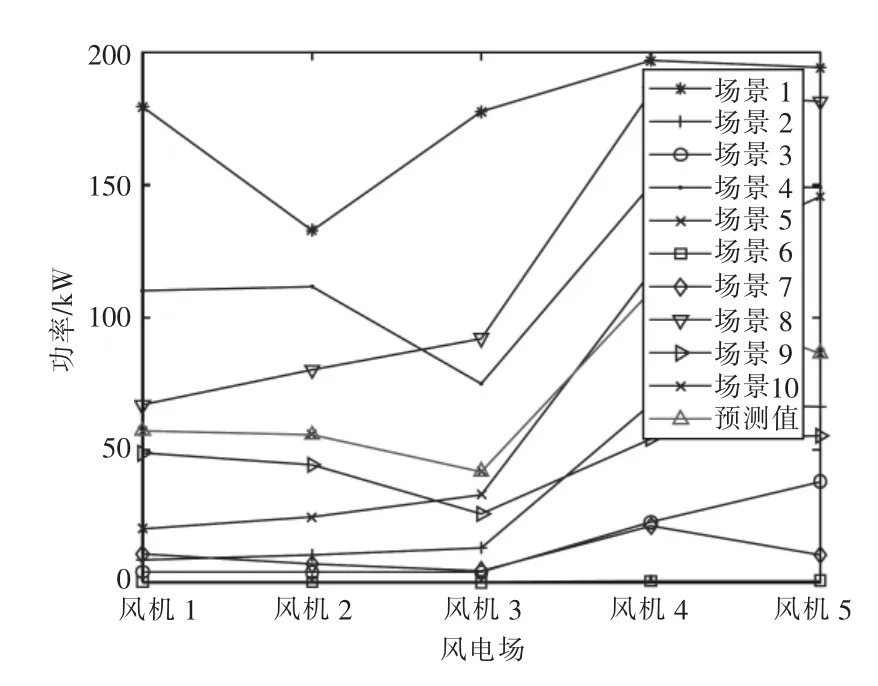
圖5 傳統場景生成法下的多風電場景

為了全面評價場景的優劣性，本文從風功率的波動性分布和歷史數據分布兩個角度來判斷生成場景是否貼合實際數據。

（1）波動性貼合度指標

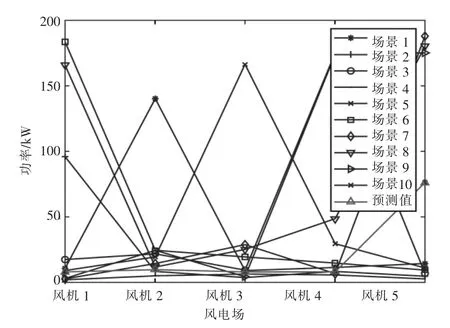
圖6 多風電相關性場景

判斷波動性貼合度，本文采用第2 章提出的協方差參數辨識的目標函數Iε，Iε表征了生成的風功率場景的波動與歷史數據的風功率波動的差異性。Iε越小，說明生成的場景越接近歷史數據的概率分布，也就越能準確描述不同風電場功率之間的相關性。

（2）歷史數據貼合度指標

本文采用文獻[24]提出的ES 指標判斷場景與歷史數據的貼合度。ES 指標著重于風電場景與實測值累積分布函數的距離。ES 指標如式（13）所示：

式中： N 為場景個數；Pj為場景j 的概率；pj為場景j 下的風電場出力；p0為風電場的實際出力。

ES 的值越小，則表明兩者越接近，那么生成的場景更符合實際的風功率分布。

不同情況下的場景評價指標計算結果如表1所示。

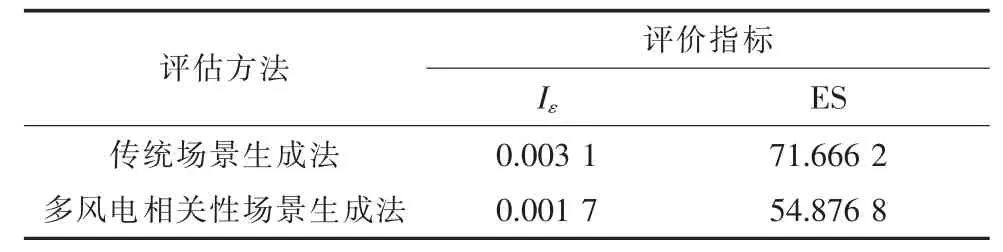
表1 場景評價指標計算結果

從表1 可以看出，在波動性和歷史數據貼合度方面，考慮了采用多風電相關性場景生成方法生成的場景比傳統場景生成法分別降低了45.16%和23.43%，說明考慮了相關性以后生成的場景的波動性分布更貼合實際波動，更加符合實際出力情況，更有利于不同風電場間無功優化的協調配合。

4.3 基于多風電場景生成的配電網隨機多目標無功優化

本文基于IEEE 33 節點系統的拓撲結構，設計了如圖7 所示的含多個風電場的配電網系統。節點1 為平衡節點；節點1 與節點2 間裝設1 臺OLTC，其標準變比為1，共11 個檔位，變比的上、下限分別為1.05 和0.95。節點29 裝設1 臺SVG，其無功調節范圍在[-300 kvar，300 kvar]。分別在節點15，17，22，25，32 接入風機DG1，DG2，DG3，DG4，DG5，額定功率為200 kW；電容器組每個電容大小均為212 μF。

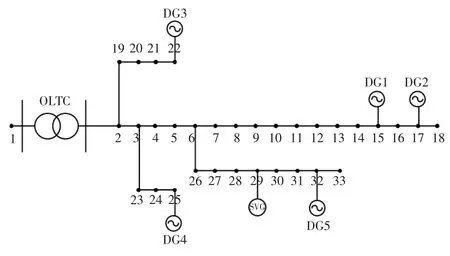
圖7 改造后的IEEE 33 節點配電系統

算法參數設置如下： 群體規模設為300，Pareto 最優解集容量閾值為100，迭代次數為30，交叉概率為0.8，變異概率為0.3。

采用本文方法優化以后的OLTC 變比為1.02，SVG 補償容量為290 kvar，電容器的最優配置方案如表2 所示。

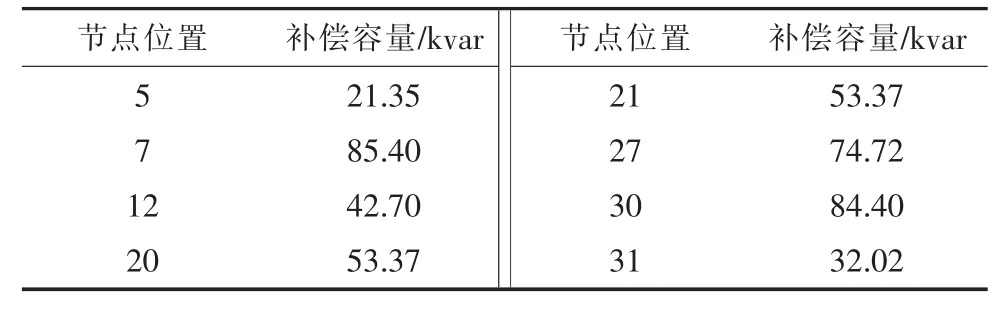
表2 電容器最優配置方案

為了便于比較，本文對基于預測值[22]、基于傳統的不考慮相關性的場景生成[25]和基于多風電相關性場景生成這3 種方法的配電網無功優化策略獲得最優配置方案下的優化效果進行比較。

3 種情況下生成的Parote 最優解分布如圖8所示。從圖中可以看出，如果不考慮場景生成，而僅用預測值進行優化，在相同的網損下，電壓偏移明顯大于考慮場景生成下的電壓偏移值。而在相同的電壓偏移下，僅用預測值進行優化得到的網損也高于考慮場景生成下的網損。說明直接采用預測值進行優化并不能很好地降低網損、提升電能質量。

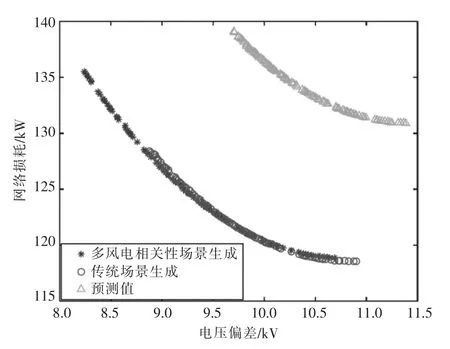
圖8 基于多風電場景生成的多目標無功優化Parote最優解分布

在考慮場景生成時，不考慮相關性的傳統場景生成方法和基于多風電相關性場景生成方法對最優解的分布影響不大[26-32]，但是考慮了不同風電場之間的相關性后，得到的最優解的范圍更大，在電壓偏移值較低的區域有更多解。經分析，這是因為考慮了相關性以后不同風電場之間能夠相互配合出力，單個風電場的波動性降低，從而增加了電壓穩定性，使電壓偏移量更小，電能質量更高。因此，采用多風電相關性場景生成方法，即基于多元隨機變量協方差辨識法考慮不同風電場之間相關性生成的風電場景具有更好的優化效果。

在得出最優解分布以后，本文還采用計算模糊貼近度的方法得出了接地電容的最優配置方案。表3 分別列出了基于預測值、基于傳統場景生成和基于多風電相關性場景生成這3 種方法得到的最優配置方案下的網絡損耗以及電壓偏移。

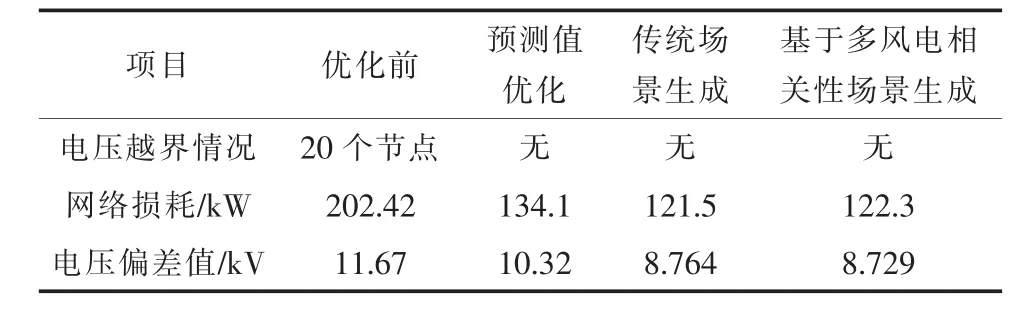
表3 優化前后各變量對比

圖9 描繪了IEEE 33 節點系統的原始電壓分布以及上述3 種情況下優化后的電壓分布。從圖中可以看出，不同情況下配電網的最優配置方案均沒有節點出現電壓越界的情況。但是基于多風電相關性場景生成獲得的配電網最優配置方案網絡損耗更小，電壓偏差值更低。這表明考慮風電場相關性場景生成的配電網優化方案電能質量更好，電能輸送效率進一步提高，具有更好的優化效果。

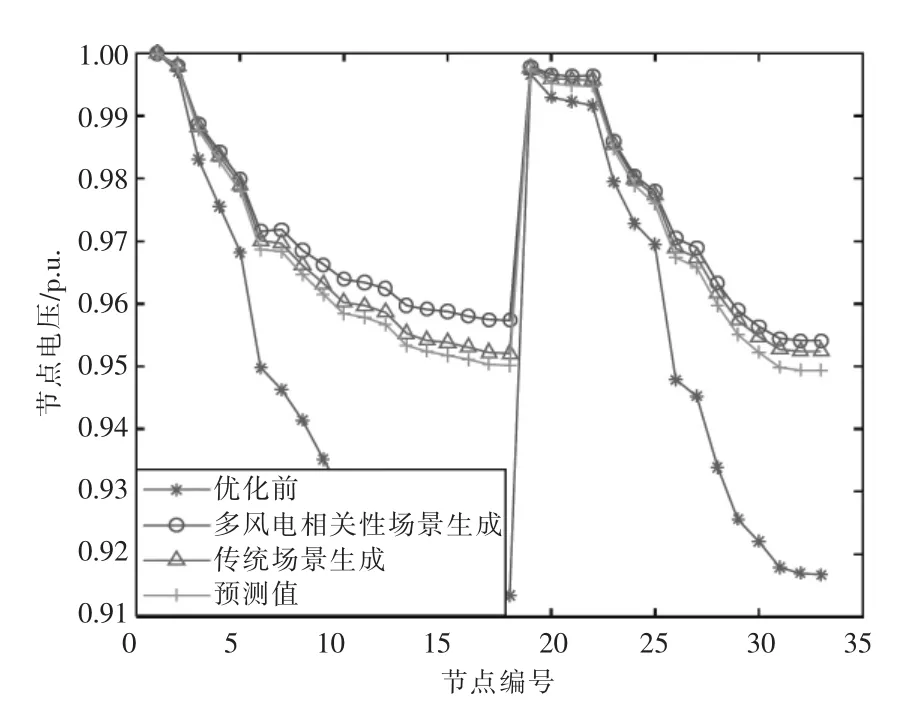
圖9 不同情況下的電壓分布

5 結論

本文主要研究了基于多風電相關性場景生成的配電網無功優化問題，主要結論概括如下：

（1）基于風電場的歷史數據建立非參數的經驗分布模型，采用多元隨機變量協方差辨識方法確定最佳協方差矩陣，生成多元隨機變量隨機數。

（2）通過逆變換抽樣得到符合相關性和波動性特征的多風電場風功率場景。利用K-means 聚類法削減得到具有代表性的多風電場景。

（3）根據生成的場景，采用NSGA-Ⅱ算法求解以網絡損耗最小以及電壓偏差最小為目標建立的配電網隨機多目標無功優化模型，運用模糊貼近度獲得電容器組最優配置方案。

（4）以IEEE 33 節點配電網無功優化問題為例，對比分析了基于預測值、基于傳統場景生成方法和本文方法獲得場景的波動性貼合度、歷史數據貼合度以及最優配置方案優化效果。結果表明，本文提出的方法獲得場景的貼合度更好，配電網無功優化效果更經濟、更可靠。

附錄A

表A1 各個風電場t location-scale 分布參數

附錄B

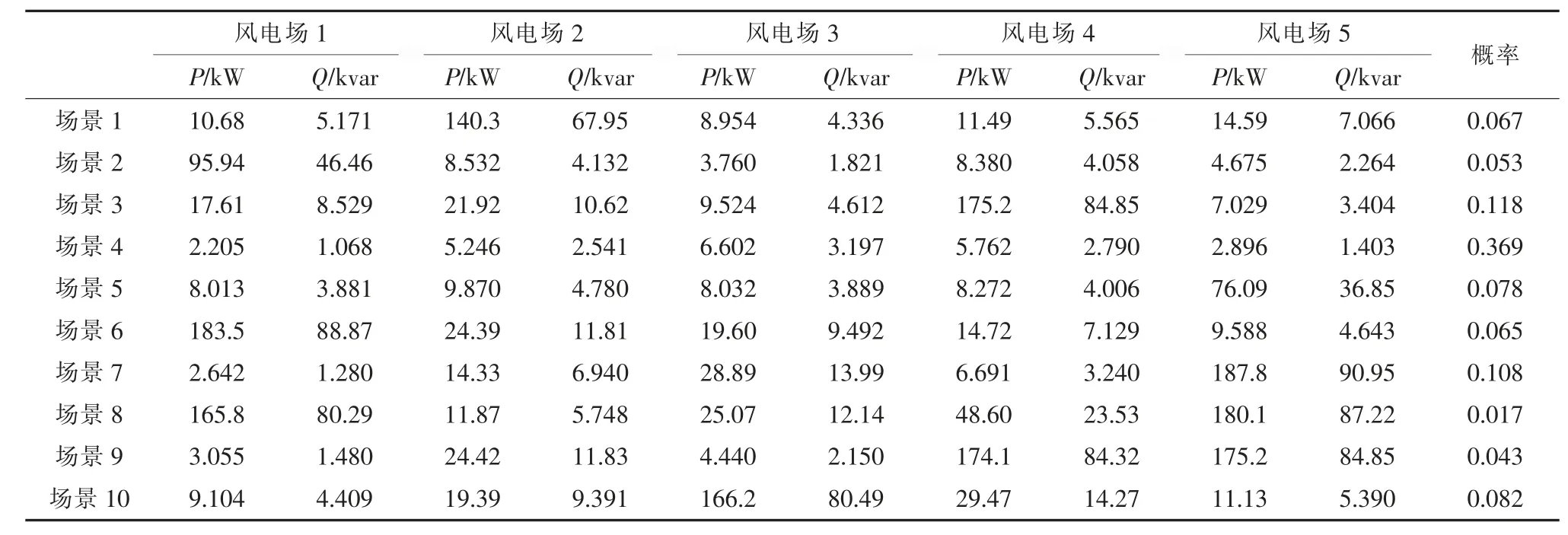
表B1 傳統場景生成及其概率

表B2 多風電相關性場景生成及其概率