嘉峪關光化樓磚墻結構對抗震性能的影響

巴振寧 焦鵬 劉冰松 張翔

摘要：以嘉峪關光化樓為研究對象，基于榫卯、斗拱節點、柱墻接觸之間的關系，利用ANSYS軟件分別建立了純木結構與磚木混合結構的光化樓模型。通過模態分析和輸入多種地震波進行動力時程分析，結果表明：①磚墻結構大大提高了光化樓低階自振頻率，在高階振型中自振頻率的差距逐漸減小;②磚墻結構使結構在地震時程分析下的加速度峰值有了明顯增大，這與結構自振周期降低有關;③在地震作用下，磚墻結構使結構的位移峰值顯著減小，對防止木構架側移倒塌有很大貢獻;④純木結構模型位移反應較大，但仍小于木結構建筑彈塑性層間位移角1/50的限值;⑤在Ⅷ度罕遇地震作用下，磚墻結構底部及開洞處的塑性應變較大，具體可能表現為磚墻底部以及磚墻與木門連接處出現裂縫。

關鍵詞：光化樓;純木結構;磚木混合結構;模態分析;時程分析

0 引言

中國木結構建筑文化源遠流長，留有許多寶貴的文化結晶。嘉峪關建筑群始建于公元1372年，建成后經歷了多次的損毀與修繕。1987年，嘉峪關建筑群被聯合國教科文組織列入《世界文化遺產名錄》。我國是一個地震多發的國家，嘉峪關位于世界上最大的地震帶“喜馬拉雅—環太平洋地震帶”的作用區。因此對嘉峪關木構城樓進行抗震研究和保護，具有十分重要的意義。

國內外一些建筑大師，如梁思成（1983）、伊東忠太和陳清泉（2014）對我國的古建筑進行了系統的研究。隨著力學學科體系的發展，對結構的整體和不同構件的研究也有了迅速發展。周乾等（2014）建立故宮太和殿有限元模型響應譜，分析了在Ⅷ度罕遇地震作用下，太和殿結構的內力及變形;謝啟芳等（2018）以西安鐘樓為研究對象，建立了縮尺比例為1：6的模型進行振動臺實驗，得到了在不同幅值、不同地震波作用下模型的加速度、位移和破壞形態;潘毅等（2019）以饒益寺大佛殿和保國寺的鋪作層為參照，設計了4種不同的鋪作層布置模型，進行動力時程分析，研究不同鋪作層布置對地震激勵作用下結構產生的動力響應的影響;Uchida等（2004）、Kawai等（2006）和Fujita等（2008）分別對日本傳統的多層木塔與廟宇結構進行了側向靜力試驗，結合日本地區地震記錄數據，建立層模型并分析在地震作用下各節點與結構整體的動力響應特點。

上述研究分別對不同的木結構建筑進行了研究分析，但大多集中于受力結構，而忽略了圍護結構。木結構古建筑的形制復雜，構件的應用組合多樣，再加上木材的特性，不同建筑都有其獨特的結構狀態，值得研究。嘉峪關木構城樓第一層為磚木混合結構，第二、三層為木結構。一層金柱嵌固在磚砌體墻內，因此磚墻對木結構力學性能勢必有所影響。本文采用有限元數值模擬方法，建立嘉峪關光化樓木結構有限元分析模型與磚木混合結構有限元分析模型，分別輸入Ⅷ度多遇、設防與罕遇的地震波激勵，分析磚墻結構對抗震性能的影響。

1 數值模型

1.1 光化樓簡介

光化樓始建于公元1506年，位于嘉峪關東城臺之上，城臺平面為矩形，臺面采用條磚十字縫墁地，城臺下有拱券式門洞。嘉峪關建筑群如圖1所示。

光化樓為典型的抬梁木構城樓，屋頂樣式采用單檐歇山頂式。由圖2可見，一層柱分內外兩周，共計28根（檐柱18根、金柱10根），為貫穿三層的通柱，層高約4.4 m;二層有外廊，柱分內外兩周，廊柱18根，層高約4 m;三層無外廊，共計檐柱10根，層高約3.7 m。建筑一層為磚木結構，采用磚墻，二、三層為木結構，采用槅扇，磚墻包裹金柱，厚約1.3 m，周長約41.5 m，東西兩側開門，門高2.55 m、寬2.12 m。

1.2 單元選擇

光化樓模型采用ANSYS有限元分析軟件進行模擬。對于傳統木結構古建筑，結構主體部分主要由梁柱構架組成，采用Beam188 單元對其進行數值模擬。Beam 188單元在每個節點上有6個自由度，包括沿X，Y，Z軸的線位移和繞X，Y，Z軸的角位移，適合分析細長到中等長度的梁結構。

對于屋蓋、樓板和磚墻結構，采用Shell181單元進行建模。該單元內各節點含有6個自由度，常用于模擬平板和曲殼等形式的結構，能夠傳遞單元彎矩并在非線性計算中考慮殼厚度的變化。

對于木結構榫卯、斗拱節點，采用Combin14彈簧單元進行模擬，該彈簧單元可以傳遞軸力、剪力和彎矩，通過2個節點來定義，可以設置6個方向的彈簧剛度。

1.3 材料參數及邊界條件設置

對木結構進行結構分析驗算時，材料性能強度不僅要滿足《木結構設計規范》（GB 50005—2017）的規定，還應該考慮荷載長期作用和木質老化的影響，對木材的各項力學性能指標給予調整。本文將木材本構關系簡化為理想彈塑性，遵循Hill屈服準則。

由于對嘉峪關光化樓缺乏直接的實驗數據，參照祝松濤（2013）對嘉峪關關樓的研究，其木材為紅松，為正交異性材料，木材參數見表1。將紅松的各個方向材料性能簡化為理想彈塑性，此處假定木材的受拉與受壓方向的屈服強度相同，采用Hill準則與BISO模型結合的方式進行定義，即通過Hill準則定義6個方向不同的屈服強度，采用BISO模型進行切線模量的定義，此處切線模量定義為0，各個方向屈服強度值參考王玉迪（2018）對紅松木材的研究，見表2，理想彈塑性模型如圖3所示。其中考慮到光化樓修建完成距今已經超過500年，根據《古建筑木結構維護與加固技術規范》（GB 50165—92）中對考慮長期荷載作用和木質老化調整系數的規定，對強度等性能均乘以0.7的折減系數。

朱才輝等（2019）曾對同為明代建筑的西安明代城墻以及鐘樓的磚墻砌體進行過研究。結合其得出的磚墻砌體等效力學參數，并參考《砌體結構設計規范》（GB 50003—2011），本文采用的磚砌體墻材料力學參數見表3。

式中：σD，εD為考慮損傷因子的應力與應變;損傷因子D為0～1，數值越大表示結構的損傷程度越大，光化樓磚墻結構無明顯破壞且本文主要考慮磚墻結構對抗震性能的影響，因此D取0;ε0為對應于砌體抗壓平均值的應變，根據朱才輝等（2019）的研究，取0.003。砌體結構的應力-應變曲線如圖4所示，采用MISO模型進行定義。

斗拱是古建筑中主要的結構連接形式，由多層木塊交疊、咬合而成，其動力學特性十分復雜，在地震等外力荷載作用下，斗拱可以視為一組彈簧，通過自身擠壓變形，減緩結構的變形，并且吸收掉一部分振動能量。本文采用Combin14彈簧來模擬斗拱半剛性的特性。梁柱榫卯節點與斗拱，均具有半剛性連接特點，同樣簡化為Combin14單元。斗拱、榫卯各個方向自由度的剛度值參考高大峰等（2008）、蘇軍（2008）的試驗以及數值模擬分析結果，節點剛度取值見表4。

中國古建筑結構普遍通過柱礎與地基相連接，柱根一般擱置在礎石之上，在主體結構的重力作用下，礎石能夠為柱腳提供豎直方向的支撐力和

水平方向上一定的摩擦力，對柱根的轉動具有微弱的限制。參考高大峰等（2008）、蘇軍（2008）中對木結構古建筑的處理方法，本文將柱腳與礎石的連接節點近似簡化為鉸接節點;光化樓一層磚墻將金柱包裹在內，牢牢嵌固，將墻柱連接設置為剛接。

1.4 建立數值模型

光化樓的梁柱框架組成了主要的結構受力體系，主體結構可以劃分為屋架層、鋪作層以及柱網層。屋架層主要由梁、枋、檁條等組成的梁架體系來支撐屋頂以及傳遞上部荷載;鋪作層主要以斗拱為主，對各層起承上啟下的作用;柱網層是光化樓結構的豎向支撐部分，將整棟樓所承擔的荷載傳導到臺基上。對主體結構逐層建立無磚墻結構數值模型（以下簡稱模型1），如圖5a所示。

磚砌體墻是由砌塊混合砂漿等粘合劑制作成的受力結構，主要受到砌塊材料性能的影響，但由于砂漿等粘合劑的材料特性與磚砌體存在顯著差異，所以砂漿等粘合劑對結構整體的影響也不可忽視。且結構的整體力學性能還受到諸如磚砌體尺寸、砌縫的寬度以及磚墻的砌筑方式、工藝水平等因素的影響。

目前，常用的磚砌體墻的有限元建模方法包含分離式和整體式2種。分離式建模方法就是對磚砌體墻的2種材料分別進行建模，并對2種材料接

觸面做出定義以模擬其工作性能。整體式建模方法就是將磚砌體墻視為均質的各向同性材料，忽略結構模型中局部的材質差異。采取整體式建模方法時，可以適當簡化磚墻結構的材料本構與力學參數，大大簡化了建模難度和運算過程，適合于將磚砌體墻的看作宏觀整體的有限元結構分析，本文采用該方法將磚墻結構按照圖紙進行建模，其中東西向磚墻按照門尺寸進行開洞，尺寸為2.12 m×2.55 m，最終建立有磚墻結構數值模型（簡稱模型2），如圖5b所示。

2 模態分析

模態分析是研究結構系統特性的一種方法，主要用于求解結構的自振頻率、模態振型等固有振動特性。對于古建筑來講，對其地震荷載作用下振型的分析，是結構動力學分析的基礎。通常情況下高階模態的權重遠低于低階模態，一般取前幾階模態進行分析。

本文采用子空間法提取數值模型模態，子空間法在提取中大型模型且小于40階振型時具有較高的精度。數值模型振型頻率值變化如圖6所示。由圖可知，嘉峪關光化樓數值模型前20階的頻率均分布至0～10 Hz，自振頻率隨階數增大逐漸增大，在高階時增長逐漸變緩。

磚墻結構的存在使結構低階自振周期顯著減低，在高階振型中自振頻率逐漸趨于一致，對結構整體剛度有較大的貢獻，對光化樓整體的動力性能有顯著影響。

3 抗震性能分析

3.1 地震波的選取

根據《建筑抗震設計規范》（GB 50011—2010），嘉峪關處于Ⅷ度抗震設防區，基本加速度為0.2 g，進行時程分析時根據多遇地震、設防地震、罕遇地震分別調幅為70 gal，200 gal，400 gal 3種不同加速度峰值的地震波。選取的地震波分別為El-Centro波、Taft波與蘭州波。以200 gal峰值地震波為例，其地震影響系數如圖7所示。

3.2 阻尼確定

阻尼作為一種能量耗散機制，使振動等運動隨時間減弱并最終停止。采用瑞利阻尼進行設置，其阻尼矩陣C由質量矩陣M和剛度矩陣K表示為：

根據俞茂宏等（1991）、Fang等（2001a，b）對木結構整體動力試驗測試與現場環境脈動試驗，測定其阻尼比為2%～9%，一般小于5%，本文阻尼比取3.5%。根據之前模態分析結果，模型1：α=0.241 3，β=0.003 336;模型2：α=0.498 1，β=0.001 605。

3.3 加速度反應分析

對模型輸入水平雙向地震波，由于Y向建筑尺寸小于X向，故輸入地震波時Y向與X向峰值加速度比為1∶ 0.85，采用前文所述9條地震動記錄進行輸入，模型加載工況見表5。

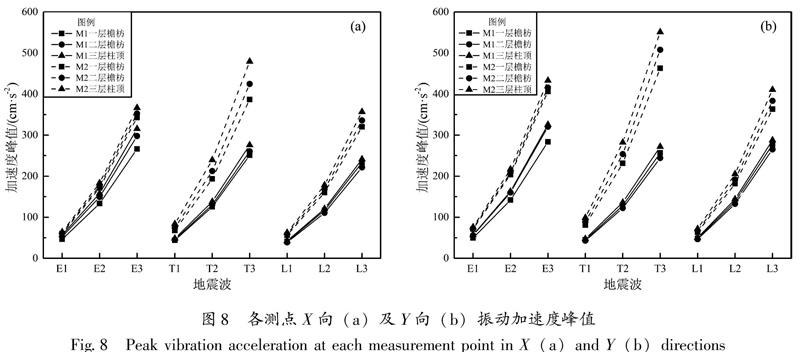
為分析不同地震加速度峰值下光化樓地震響應，分別選擇一層檐枋、二層檐枋、三層柱頂位置，提取其動力響應數據。所有工況作用下的測點的振動加速度峰值如圖8所示，所有工況作用下的放大系數平均值見表6，7。

由圖8，表6可知：在水平地震作用下，隨地震波激勵的增加，各層的加速度峰值也隨之增大。模型1（M1）加速度響應放大均小于1，模型2（M2）加速度響應值均有所提高，尤其是在Taft波作用下，加速度響應峰值增大1倍左右，這與磚墻結構降低了結構的自振周期，使其接近Taft波的卓越周期有關。

3.4 位移反應分析

選擇一層檐枋、二層檐枋、三層柱頂位置，提取其位移響應數據。由于文章篇幅限制，僅展示模型1與模型2三層柱頂在L1，L2，L3三種工況作用下的位移時程曲線如圖9所示，所有工況位移峰值見表7。

由圖9，表7可知，在水平地震作用下，考慮磚墻結構的情況下，各層位移的相應峰值均減小，這反映了磚墻結構對木構架的位移有很強的約束作用，對防止木構架側移倒塌有很大貢獻。模型1在峰值為400 gal的El-Centro波作用下短軸向和長軸向出現最大層架位移角，分別為1/68和1/111，小于木結構建筑彈塑性層間位移角1/50的限值。

3.5 墻體塑性應變

光化樓開洞處橫墻、未開洞處橫墻以及縱墻在400 gal的El-Centro波作用下產生的等效塑性應變情況如圖10所示。由圖可知，未開洞墻體底部的塑性應變明顯高于上部，開洞墻體的塑性應變在底部與開洞部位更為明顯。這表明墻體在Ⅷ度罕遇地震波作用下，墻體底部以及墻體與木門連接處容易出現裂縫等震害。

4 結論

本文以嘉峪關光化樓為原型，根據其一樓為磚木混合結構的特點，建立了有限元數值模型，通過動力時程分析，討論了磚墻結構對光化樓抗震性能的影響，得到以下結論：

（1）金柱與磚墻結構牢牢嵌固在一起，形成環箍效應，大大高了結構的抗側剛度。在模態分析時，磚墻結構的存在對結構的低階振型影響較大，光化樓結構的低階自振頻率顯著提高，高階自振頻率與無磚墻結構自振頻率隨振型階數的增加逐漸相等。

（2）磚墻結構的存在使建筑物加速度響應峰值有所提高，這與建筑物自振周期的變小有關。

（3）磚墻結構使建筑物位移峰值顯著降低，有助于防止木結構位移過大產生側移傾覆。

（4）對層間位移角進行了計算，嘉峪關光化樓在不同地震波作用下產生的最大層間位移角均符合相關規范的限值規定。

（5）在Ⅷ度罕遇地震作用下，墻體的底部與開洞處的塑性變形較大，墻體底部以及與木門連接處易產生裂縫。

參考文獻：

高大峰，趙鴻鐵，薛建陽.2008.木結構古建筑中斗栱與榫卯節點的抗震性能—試驗研究[J].自然災害學報，17（2）：58-64.

梁思成.1983.營造法式注釋[M].北京：中國建筑工業出版社.

劉桂秋.2005.砌體結構基本受力性能的研究[D].長沙：湖南大學.

潘毅，袁雙，郭瑞，等.2019.鋪作層布置對古建筑木結構抗震性能的影響[J].土木工程學報，52（3）：29-40.

蘇軍.2008.中國木結構古建筑抗震性能的研究[D].西安：西安建筑科技大學.

王玉迪.2018.考慮松動殘損直榫節點的多層木結構古建筑抗震性能分析[D].西安：西安建筑科技大學.

謝啟芳，王龍，張利朋，等.2018.西安鐘樓木結構模型振動臺試驗研究[J].建筑結構學報，39（12）：128-138.

伊東忠太，陳清泉.2014.中國建筑史[M].長沙：湖南大學出版社.

俞茂宏，劉曉東，方東平，等.1991.西安北門箭樓靜力與動力特性的試驗研究[J].西安交通大學學報，25（3）：55-62.

周乾，閆維明，關宏志，等.2014.罕遇地震作用下故宮太和殿抗震性能研究[J].建筑結構學報，35（S1）：25-32.

朱才輝，劉欽佩，周遠強.2019.古建筑磚-土結構力學性能及裂縫成因分析[J].建筑結構學報，40（9）：157-186.

祝松濤.2013.嘉峪關關樓抗震性能分析及研究保護[D].西安：西安建筑科技大學.