路基凍脹對CRTSⅢ型板式無砟軌道受力和變形的影響研究

徐新玉,崔建榮

(1.江蘇聯合職業技術學院蘇州建設交通分院,江蘇蘇州 215104； 2.蘇州大學軌道交通學院,江蘇蘇州 215131)

引言

無砟軌道以其少維修、高舒適度和強耐久性等優點在我國高速鐵路中應用廣泛[1-6]，我國嚴寒地區的高速鐵路里程已達5 500 km[7]，然而嚴寒地區的路基凍脹問題不可避免[8-9]，一旦發生路基凍脹必然影響無砟軌道的受力和耐久性。作為自主研發的CRTSⅢ型板式無砟軌道已在我國盤營等嚴寒地區應用，另外我國正承擔設計的莫斯科至喀山高速鐵路擬采用CRTSⅢ型板式無砟軌道。因此，研究路基凍脹對CRTSⅢ型板式無砟軌道結構受力的影響具有重要的理論意義和工程價值。

近年來，國內外學者開展了路基凍脹對無砟軌道的影響研究[10-19]，Ma Fuxun等利用GPS分析了溫度變化下路基凍脹的變化規律[10]；趙國堂研究了嚴寒地區的路基凍脹特征，建立了路基凍脹變形與CRTSⅠ型板式無砟軌道不平順的對應關系，分析了路基凍脹對無砟軌道受力的影響，提出了嚴寒地區無砟軌道路基凍脹管理標準的確定方法[11-12]；王功博等基于現場監測數據，分析了路基凍脹的變形特征及過程[13]；蔡小培等通過建立CRTSⅠ型板式無砟軌道-路基空間耦合有限元模型，分析了不同路基凍脹條件下軌道結構的變形和層間離縫特征[14]；李娟[15]、郭毅[16]和趙文博[17]分別研究了高速鐵路路基凍脹對CRTSⅠ型板式無砟軌道結構靜、動力學的影響，并提出了軌道結構破壞時對應的路基凍脹限值；向俊等研究了路基凍脹-融化-沉降循環作用對板式無砟軌道變形和受力的影響[18]；楊國濤等基于動力分析，確定了CRTSⅢ型板式無砟軌道路基凍脹的控制標準[19]。現有研究成果主要針對CRTSⅠ型板式無砟軌道開展研究，但是關于路基凍脹對CRTSⅢ型板式無砟軌道受力和變形的影響缺乏研究。

本文基于有限元方法，以我國CRTSⅢ型板式無砟軌道為研究對象，建立CRTSⅢ型板式無砟軌道-路基空間耦合有限元模型，分析了路基凍脹位置、凍脹幅值和凍脹波長對無砟軌道結構受力和變形的影響，從而為嚴寒地區CRTSⅢ型板式無砟軌道路基凍脹變形控制提供理論支撐。

1 CRTSⅢ型板式無砟軌道路基凍脹計算模型及參數

1.1 有限元模型

路基上CRTSⅢ型板式無砟軌道由鋼軌、扣件系統、預制軌道板、自密實混凝土調整層、隔離層和混凝土底座板組成[20]。建立有限元模型時，鋼軌采用梁單元模擬，扣件系統采用線性彈簧單元模擬，軌道板、自密實混凝土、隔離層、底座板和路基基床表層均采用實體單元模擬，由于CRTSⅢ型板式無砟軌道的軌道板與自密實混凝土層采用門型鋼筋連接，故模型中軌道板與自密實混凝土層間采用共用節點處理。考慮路基凍脹時自密實混凝土層與隔離層、隔離層與底座板、底座板與路基基床表層間可能產生離縫，模型中自密實混凝土層與隔離層、隔離層與底座板、底座板與路基基床表層間采用接觸單元來模擬兩者之間的黏結作用，建立的CRTSⅢ型板式無砟軌道有限元模型如圖1所示。

圖1 CRTSⅢ型板式無砟軌道-路基空間耦合有限元模型

1.2 計算參數

有限元模型中，鋼軌采用CH60N鋼軌，扣件采用WJ-8B型扣件，扣件間距取為0.63 m，扣件系統的縱向、橫向和垂向的剛度分別取為30，30 kN/mm和50 kN/mm。軌道板為C60混凝土，寬度為2.5 m，厚度0.2 m，長度為5.6 m，彈性模量為36.0 GPa；自密實混凝土層為C40混凝土，寬度為2.5 m，厚度為0.09 m，長度為5.6 m，彈性模量為32.5 GPa；底座板為C40混凝土，寬度為3.1 m，厚度為0.3 m，長度為16.99 m，彈性模量為32.5 GPa，路基基床表層彈性模量取120 MPa，寬度為3.1 m，厚度取為0.5 m。

路基凍脹采用余弦形式[14]，分別作用在底座板接縫附近(工況A)、軌道板板縫附近(工況B)和底座板中間附近(工況C)，路基凍脹作用位置如圖2所示。

圖2 凍脹作用位置

2 路基凍脹對軌道變形和受力的影響

2.1 路基凍脹位置的影響

當路基凍脹曲線波長為20 m，凍脹幅值為10 mm時，不同路基凍脹位置下軌道結構各層的變形如圖3所示。

從圖3可見，當路基發生凍脹時，軌道結構各層變形具有一定的跟隨性，鋼軌、自密實混凝土層、底座板的垂向變形逐漸減小。當路基凍脹作用在不同位置時，自密實混凝土層與底座板、底座板與路基基床表層的層間離縫主要發生在路基凍脹波峰和波底。工況A下，自密實混凝土層與底座板、底座板與路基基床表層的最大離縫值分別為0.133 mm和0.741 mm。工況B下自密實混凝土層與底座板、底座板與路基基床表層的最大離縫值分別為0.180 mm和0.750 mm。工況C下自密實混凝土層與底座板、底座板與路基基床表層的最大離縫值分別為0.229 mm和0.976 mm。可見，路基凍脹作用下，底座板與路基基床表層的離縫值遠大于自密實混凝土層與底座板的離縫值。

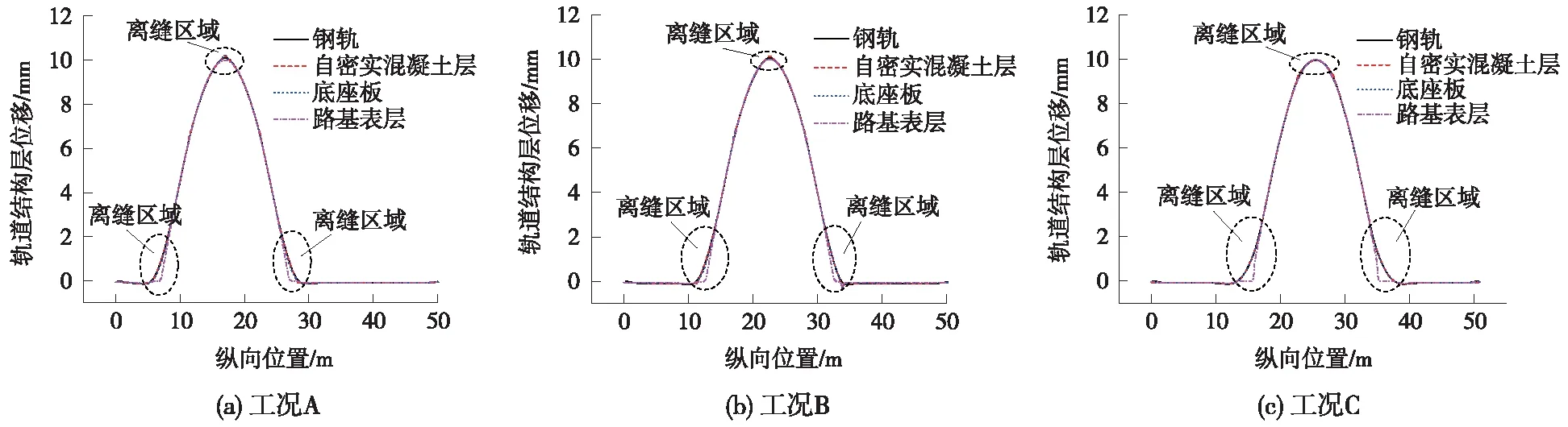
圖3 不同凍脹位置下軌道結構位移曲線

不同路基凍脹位置下，軌道結構各層的應力如表1所示。

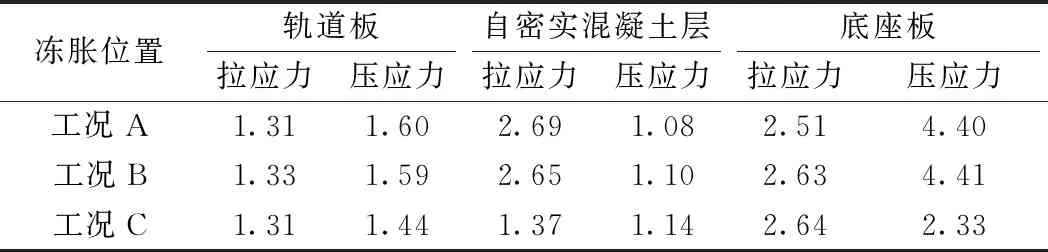
表1 不同凍脹位置下軌道結構各層的最大應力 MPa

從表1可見，軌道結構受力與路基凍脹作用位置有關，路基凍脹發生在位置A和位置B時，軌道板和自密實混凝土層所受應力大于凍脹作用于位置C。路基凍脹發生在位置B和位置C時，底座板所受拉應力大于凍脹發生在位置A處，說明路基凍脹發生在底座板下部時對底座板受力更加不利。

由于當路基凍脹發生在底座板板中時，軌道結構層間離縫和底座板受力均最大，故下文均以路基凍脹發生在底座板板中進行分析。

2.2 路基凍脹幅值的影響

當路基凍脹波長為20 m，凍脹幅值分別取為2，5，8，10，15 mm和20 mm時，不同路基凍脹幅值下軌道結構各層的位移和應力分別如表2、表3所示。

表2 不同凍脹幅值下軌道結構各層的位移 mm

從表2可知，軌道結構各層位移、層間離縫值均隨路基凍脹幅值的增大而增大。根據工程實踐，當離縫值大于1.0 mm時，認為軌道結構出現脫空現象，會對行車產生不利影響[12]。當路基凍脹幅值為20 mm時，自密實混凝土層與底座板的離縫值為0.66 mm，可認為不存在脫空現象。當路基凍脹幅值為10 mm時，底座板與路基基床表層的層間離縫達到0.98 mm，接近層間離縫限值1 mm。考慮軌道結構的層間離縫，認為路基凍脹波長為20 m，凍脹幅值不應超過10 mm。

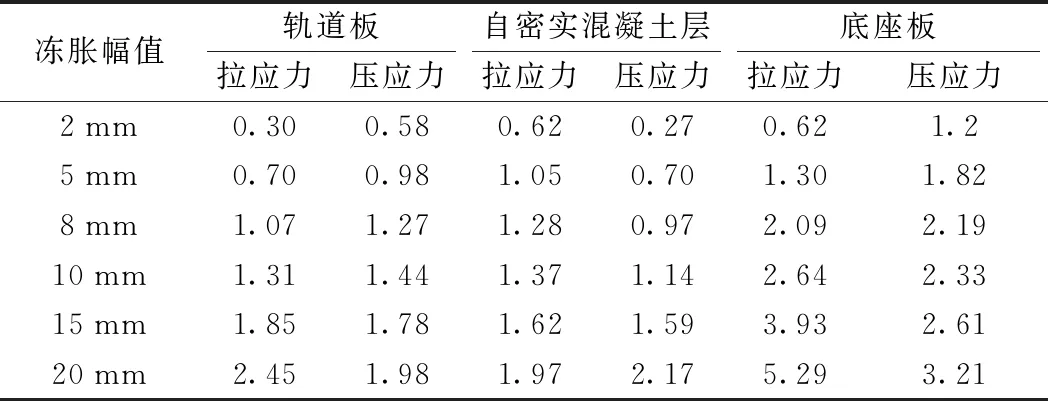
表3 不同凍脹幅值下軌道結構各層的最大應力 MPa

從表3可知，軌道結構各層的受力均隨路基凍脹幅值的增大而增大，且相同條件下，底座板所受拉應力最大，因此路基凍脹幅值受底座板所受拉應力控制。根據相關規范可知，底座板和自密實混凝土的拉應力允許值為2.7 MPa，軌道板混凝土的拉應力允許值為3.5 MPa。當路基凍脹波長為20 m，凍脹幅值為10 mm時，底座板所受拉應力為2.64 MPa，接近底座板混凝土拉應力允許值，因此從底座板受力的角度考慮，當路基凍脹波長為20 m時，凍脹幅值不應大于10 mm。

2.3 路基凍脹波長的影響

當路基凍脹幅值為10 mm時，凍脹波長從5 m變化至30 m時，軌道結構的層間離縫變化如圖4所示。

圖4 軌道結構各層的層間離縫

從圖4可知，軌道結構各層的層間離縫值隨路基凍脹波長的增大而減小，且底座板與路基基床表層的層間離縫值遠大于自密實混凝土與底座板的層間離縫，因此，應根據底座板與路基基床表層的層間離縫值來確定路基凍脹波長對應的凍脹幅值限值。

由于在路基凍脹作用下軌道結構各層的壓應力遠小于混凝土的抗壓強度，路基凍脹幅值主要受拉應力控制，因此僅列出軌道結構各層拉應力隨路基凍脹波長的變化，如圖5所示。

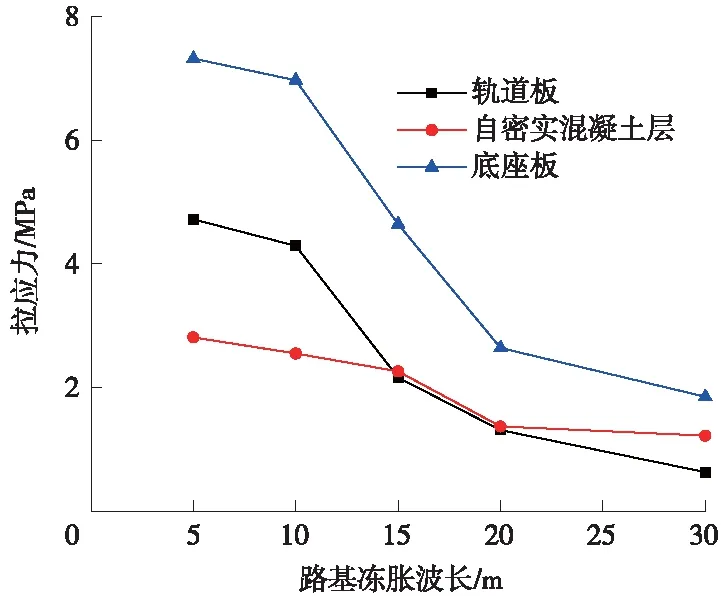
圖5 軌道結構各層拉應力

從圖5可知，軌道結構各層拉應力隨路基凍脹波長的增大而減小。當路基凍脹幅值為10 mm時，路基凍脹波長小于20 m時，底座板所受拉應力將大于底座板拉應力允許值，當路基凍脹幅值為10 mm時，路基凍脹波長應≮20 m。

2.4 路基凍脹幅值限值

路基凍脹幅值主要由底座板與路基基床表層的離縫值、底座板拉應力控制，路基凍脹作用于底座板板中時，不同路基凍脹波長和凍脹幅值下底座板與路基基床表層的離縫值、底座板拉應力變化如圖6所示。

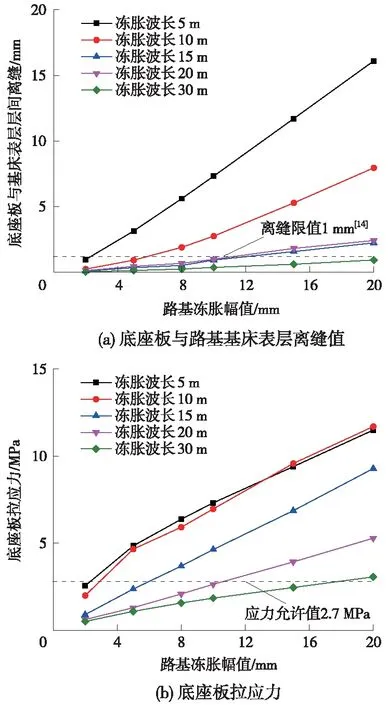
圖6 路基凍脹幅值限值

從圖6可知，當路基凍脹波長一定時，底座板與路基基床表層的層間離縫和底座板拉應力均隨路基凍脹幅值的增大而增大；當凍脹幅值一定時，底座板與路基基床表層的層間離縫和底座板拉應力均隨路基凍脹波長的增大而增大。綜合考慮底座板與路基基床表層的離縫限值和底座板混凝土允許拉應力限值，當路基凍脹波長為5 m時，路基凍脹幅值應≯2 mm；當路基凍脹波長為10～15 m時，凍脹幅值應<5 mm；路基凍脹波長為20 m時，凍脹幅值≯10 mm；路基凍脹波長為30 m時，路基凍脹幅值≯15 mm。從靜力角度考慮，路基凍脹幅值限值隨凍脹波長的增大而增大。從軌道平順性的角度，路基凍脹幅值越大，產生的不平順幅值越大，此時應綜合考慮行車安全性和平穩性來確定長波下的凍脹幅值。

3 結論

通過建立CRTSⅢ型板式無砟軌道-路基空間耦合模型，研究了路基凍脹位置、凍脹幅值和凍脹波長對無砟軌道受力和變形的影響，得到如下結論。

(1)路基凍脹作用位置對軌道結構各層的變形和受力影響較大；當路基凍脹發生在底座板板中時，軌道結構層間離縫和底座板受力均最大。

(2)隨著路基凍脹幅值的增大，軌道結構各層的變形和應力均增大；當凍脹波長為20 m，凍脹幅值超過10 mm時，底座板與路基基床表層的層間離縫值、底座板拉應力接近限值，應及時進行凍脹防治。

(3)隨著路基凍脹波長的增加，軌道結構的層間離縫和拉應力隨之減小；路基凍脹波長增大對減小層間離縫和軌道受力有利。

(4)從軌道靜力分析可知，路基凍脹幅值限值隨路基凍脹波長的增大而增大。