函數(shù)背景下平行四邊形存在性問題的解法探討
李小蘭

[摘要]平行四邊形存在性問題可用通性通法和中點公式的特殊解法求解.每一類數(shù)學問題都有通法和一些特殊方法,教學中教師應(yīng)引導(dǎo)學生善于總結(jié),勤于歸納,做到心中有題,題中有妙法.
[關(guān)鍵詞]平行四邊形;函數(shù);存在性問題;中點公式
[中圖分類號]G633.6
[文獻標識碼] A
[文章編號] 1674-6058( 2020)35-0024-02
函數(shù)背景下平行四邊形存在性問題是歷年中考數(shù)學的重要考點之一,將幾何圖形與函數(shù)相結(jié)合進行考查更是一個熱點問題,如何突破幾何中的重點章節(jié)(平行四邊形)和代數(shù)中的重點知識(函數(shù))相結(jié)合的考點,是中考數(shù)學復(fù)習的重點,因此,掌握方法,找到突破口,把問題輕松解決,是教師和學生的急切需要,下面筆者以特殊的平行四邊形——菱形和一般平行四邊形為例討論函數(shù)背景下平行四邊形存在性問題的解法,
一、函數(shù)背景下菱形存在性問題
菱形中已知三個定點求一個動點的題目難度系數(shù)較低,一般不會在大題中出現(xiàn),所以本文只論述兩個定點、兩個動點的情況.
菱形存在性問題大多是以“兩定兩動”為設(shè)問方式,其中“兩定”指的是四邊形四個頂點,其中有兩個頂點的坐標是確定的或者是可求解的;“兩動”指的是其中一個動點在一條直線或者拋物線上,另一個動點是平面內(nèi)任意一點或者該動點也在一條直線或者拋物線上,
探究菱形存在性問題的具體方法如下:
(1)根據(jù)題意找出兩個定點;
(2)分情況討論:已知兩個定點去探究菱形時,以兩個定點確定的線段作為要探究的菱形的對角線或邊長畫出符合題意的菱形,結(jié)合題于要求找出滿足條件的菱形;
(3)利用菱形的性質(zhì)得出等量或列方程求點的坐標,要具體情況具體分析,有時也可利用直線的解析式聯(lián)立方程組,根據(jù)方程組的解為交點坐標或由平移得到點的坐標,
現(xiàn)列舉幾例加以說明.
[案例1]點A和點B為平面內(nèi)兩個定點,點C是直線Z上一個動點,點D是平面內(nèi)的一個動點,畫出滿足題意的菱形,
方法:要畫出滿足題意的所有菱形,可以轉(zhuǎn)化為畫等腰三角形,
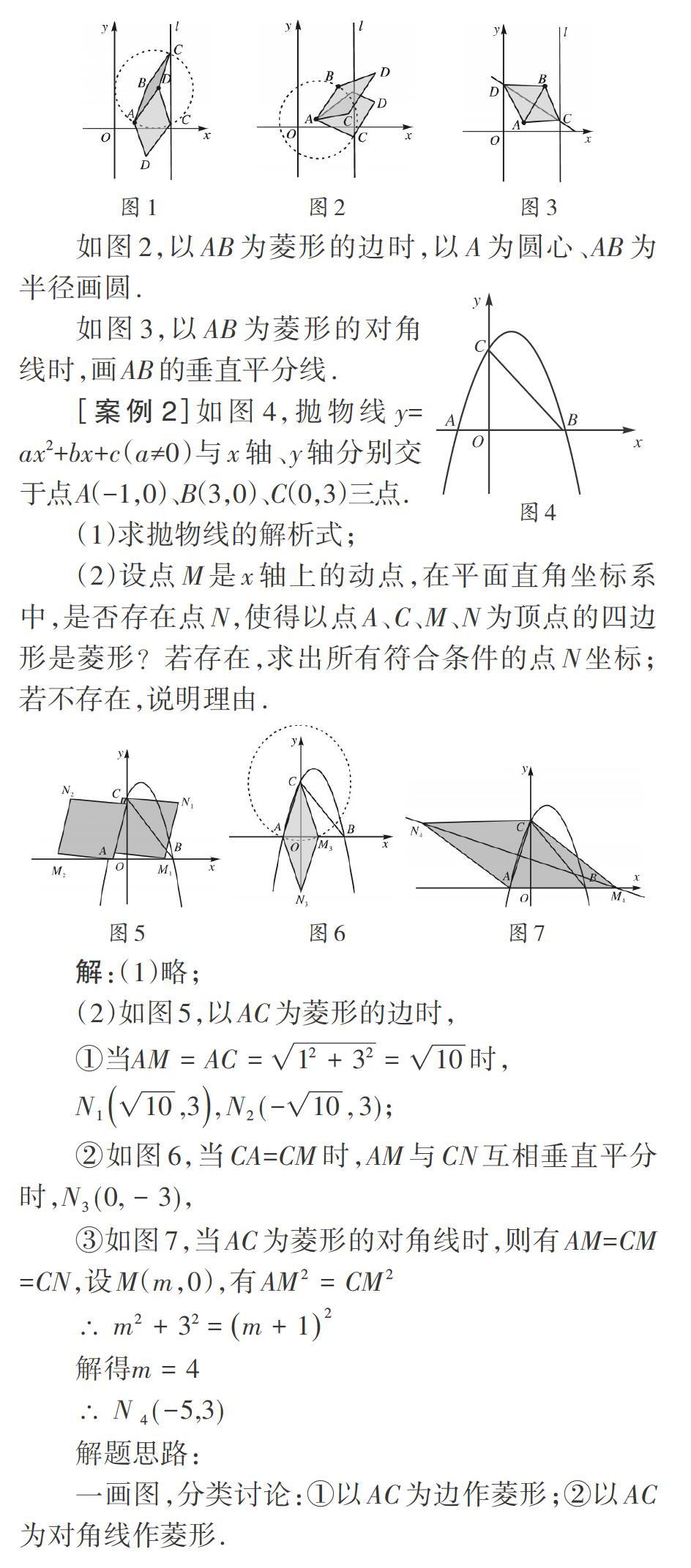
如圖1,以AB為菱形的邊時,以B為圓心、AB為半徑畫圓,
如圖2,以AB為菱形的邊時,以A為圓心、AB為半徑畫圓.
如圖3,以AB為菱形的對角線時,畫AB的垂直平分線.
[案例2]如圖4,拋物線y=ax2+bx+c(a≠0)與x軸、y軸分別交于點A(-1,0)、B(3,0)、C(0,3)三點.
(1)求拋物線的解析式;
(2)設(shè)點M是x軸上的動點,在平面直角坐標系中,是否存在點N,使得以點A、C、M、N為頂點的四邊形是菱形?若存在,求出所有符合條件的點Ⅳ坐標;若不存在,說明理由,
二求點,根據(jù)圖形選擇適當?shù)姆椒ǎ热绻垂啥ɡ怼⑵揭啤⒆飨嗨迫切蔚龋?/p>
在作圖過程中,分類討論有助于學生厘清思路,不重不漏地把圖形準確地畫出來,解決了作圖這個難點,求點的坐標方法比較開放,學生會選擇合適的方法求之,
二、平行四邊形存在性問題
平行四邊形中也存在兩種問題,一是“三定一動”,即已知三個定點求一個動點的坐標問題,這種情況只要用三定點作出三角形,并以三角形的三邊分別為對角線作出三個平行四邊形即可求出動點的坐標,本文只重點討論“兩定兩動”的情況,
前面討論的菱形也屬于平行四邊形,所以菱形的方法在平行四邊形中同樣適用,這是通性通法,下面主要討論平行四邊形的特殊解法.
[案例3]如圖8,拋物線經(jīng)過A(-5,0),B(一1,0),C(0,5)三點,頂點為們,連接AC,BC,拋物線的對稱軸為l,l與x軸交點為D,與AC交點為E,
(1)設(shè)點C'是平面內(nèi)一點,是否存在以點A,B,C',C為頂點的四邊形是平行四邊形?若存在,求出點C'的坐標;若不存在,請說明理由;
解題思路:如圖9至圖11,“三定一動”的問題,只要以BC、AC、AB分別為對角線作平行四邊形,再通過平移的方法求出點C的坐標即可.
(2)設(shè)點N是拋物線上一點,點S是x軸上一點,是否存在點Ⅳ,使得以A,E,N,S為頂點的四邊形是平行四邊形?若存在,求出點N的坐標;若不存在,請說明理由,
解題思路:①以AE為平行四邊形的邊,根據(jù)“兩動”限制的條件作出NS的三種情況(如圖12).結(jié)合圖形過Ⅳ作NT ⊥x軸,由平行四邊形性質(zhì)得到△SNT≌△AED,從而得到NT= ED=2,即可得到點Ⅳ的坐標;
②以AE為平行四邊形的對角線只有圖13 一種情況,由平行四邊形的性質(zhì)可知NE//AS,可得出N與E的縱坐標相同,即可求出點Ⅳ的坐標.
這種解法類同于前面菱形的解法,都是用分類討論的方法作圖,然后根據(jù)圖形選擇適當?shù)姆椒ㄇ蟪鳇c的坐標,既然在坐標系中解題,我們可以設(shè)法用中點公式來解決,
評析:對于平行四邊形的存在性問題,本題用了兩種方法去解決,即通性通法和中點公式法,所用的通性通法與菱形的解題方法一樣分兩步走,一是畫圖,二是求點的坐標;利用中點公式的特殊解法是通過中點公式求點的坐標,這種方法必須先設(shè)出四個點的坐標,即四個點的坐標具有共性,便直接利用公式求點,而菱形利用中點公式求點坐標卻比較麻煩,因為菱形的特殊性,每一種情況的圖形中的坐標不一致,所以利用中點公式求點的坐標必須分情況計算,有時利用通性通法更簡便,
當然,任何一種固定的解法都不利于培養(yǎng)學生的思維,但每一類數(shù)學問題都有通性通法和一些特殊方法,我們應(yīng)善于總結(jié),勤于歸納,做到心中有題,題中有妙法.
(責任編輯 陳昕)

