關注中考三角形的幾個考點
李棟
[摘要]探討中考中三角形的幾個重要考點,即三角形的三邊關系、三角形的三角關系、三角形的邊角關系,可以使學生深刻認識三角形的邊角關系,并能運用邊角關系解答相關問題,提高學生基本的幾何素養.
[關鍵詞]三角形;中考;考點
[中圖分類號]G633.6
[文獻標識碼] A
[文章編號] 1674-6058( 2020)35-0020-02
三角形的三邊關系、三角關系與邊角關系是各省市中考的重點,下面筆者對此做一探討,
考點一:三角形的三邊關系
三角形的三邊關系,是指在所有三角形中,任意兩邊相加的和,必然大于第三條邊,任意兩邊相減的差必然小于第三條邊,這樣我們可以通過已知三角形的兩邊長,求出第三條邊的取值范圍,進而求出三角形周長的取值范圍,當第三條邊取整數時,還可以確定第三條邊的長,對于特殊三角形,如直角三角形,它的三邊還符合勾股定理,等腰三角形,它的三邊存在底邊大于0小于二分之一周長,腰長大于0的規律.
[例1]解答下列相互關聯的三個問題:
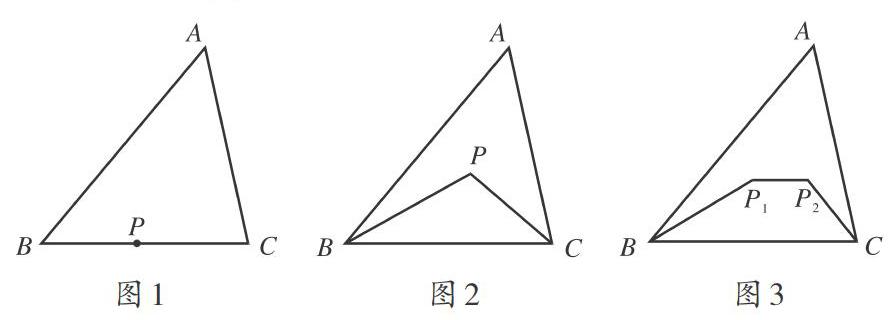
(l)觀察圖1,已知點P是三角形ABC的BC邊上的一點,試比較BP+PC與AB+AC之間的大小關系.
(2)觀察圖2,當點P從三角形的一邊上移到三角形的內部時,試比較C△BPC與C△ABC的大小關系.
(3)觀察圖3,當一個點P變化為兩個點P1、P2,試比較C 四邊形BP1P2C與C△ABC的大小關系,
解析:(1)根據三角形三邊關系定理得出BP+PC< AB十AC.理由:三角形兩邊之和大于第三條邊;
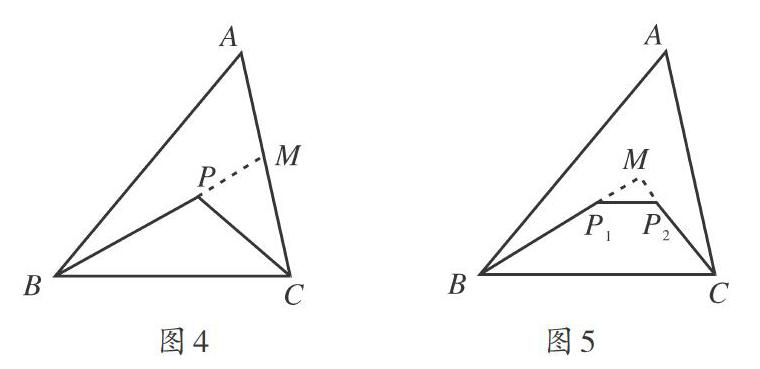
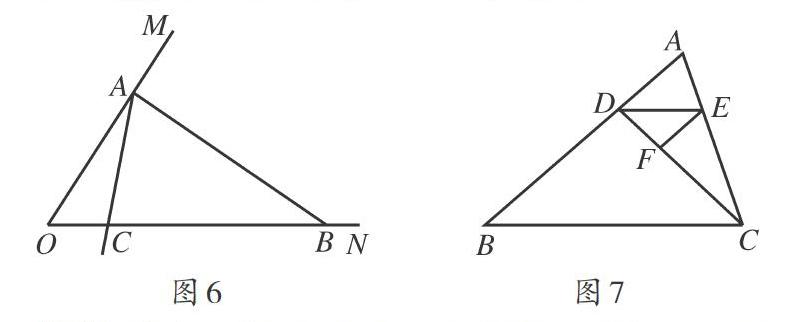
(2)可延長BP交AC于M,根據三角形三邊關系定理得出:△BPC的周長<△ABC的周長,理由:如圖4,延長BP交AC于M,在△ABM中,BP+ PM< AB十AM,在△PMC中,PC< PM+ MC,兩式相加得BP+PC (3)分別延長BP1、CP2交于們,再根據(2)中得出的結論,可得出:四邊形BPIP2C的周長<△ABC的周長,理由:如圖5,分別延長BP,、CP,交于M,由(2)知,BM+CM< AB+ AC,又P1、P2 考點二:三角形的三角關系 三角形的三角關系,是指三角形的三個內角相加必為180°,即三角形內角和定理,已知三角形兩個內角的度數可以求出第三個角的度數,此內角和定理決定了三角形最多有一個直角或鈍角,最多有三個銳角,最少有兩個銳角,因為三角形的內角與相鄰的外角是互補關系,所以三角形的一組外角中,最多有一個銳角,最多有三個鈍角. [例2]閱讀下列材料并解答問題:我們規定,三倍角三角形是指三角形中,有兩個內角的關系是三倍關系,當三角形ABC的三個內角分別為105°、35°、40°時,三角形ABC就是一個三倍角三角形,反過來,當三角形ABC是三倍角三角形,那么三角形ABC中必有兩個角是三倍關系. (l)在圖6中,∠O的度數為60°,BA垂直于∠O的一邊OM,垂足為點A,判斷△AOB是否是三倍角三角形,并說明理由. (2)在(1)的條件下,以A為端點畫射線AD,交線段OB于點C(點C不與點O、點日重合).若△AOC是三倍角三角形,求∠ACB的度數. (3)圖7,在三角形ABC中,DE平分∠ADC,且∠EFC與∠BDC互補,∠DEF與∠B相等,如果三角形BCD是三倍角三角形,那么∠B的度數是多少? 解析:(1)∵AB⊥OM,∴∠OAB= 90°,∴∠ABO=90° -∠MON= 30°,∵∠OAB=3∠ABO,∴△AOB為三倍角三角形; (2)。∵∠MON= 60°,∴當∠OAC= -∠AOB= 20°時,△AOC是三倍角三角形'..LACB= LOAC+∠AOB= 80°,當∠OAC=3∠ACO,即∠OAC= 30°時,△AOC是三倍角三角形.∴∠ACB= 90°; (3)因為∠EFC與∠BDC互補,∠LADC與∠BDC互補,根據同角的補角相等,得∠EFC=∠ADC,根據“同位角相等,兩直線平行”,得AD∥EF,根據“兩直線平行,內錯角相等”,得∠DEF=∠ADE,結合已知中的等角,得∠B=∠ADE,再根據平行線的判定方法,得DE∥BC,根據題中的角平分線,得∠ADE=∠CDE,這樣∠B=∠BCD.因為△BCD是三倍角三角形,所以應分兩種情況討論.(1)當∠BDC=3 ∠B時,根據三角形內角和定理,得∠BDC+ ∠BCD+ ∠B= 180°,所以5∠B= 180°,∠B=36°;(2)當∠B=3∠BDC時,7/3∠B=180°,∠B=540°/7 考點三:三角形的邊角關系 三角形的邊角之間最基本的關系是較大的邊對的角也較大,較大角對的邊也較長.三角形的邊角關系還包括正弦定理、余弦定理及射影定理,它們是指在三角形中,每條邊與它相對的角的正弦值相比,其比值都相等;每一邊的平方,與其他兩邊的平方和減去兩邊與夾角余弦的積的兩倍之間有相等關系;兩邊在第三邊上的投影相加,剛好等于第三邊,在直角三角形中,四個銳角三角函數講的也是三角形的邊角關系. [例3]閱讀下列材料:在圖8中,設三角形ABC的三邊分別為a、b、c,那么三角形ABC的面積有如下三種表示方法,即1/2ab sin C、1/2ac sinB、1/2bc sinA 證明:在圖8中,ADIBC,垂足為點D,在直角三角形ABD中,由正弦概念,得。inB:AD,所以AD:c.sinB,根據三角形的面積公式得三角形ABC的面積為1/2BC-AD=1/2ac sinB,如果利用∠C的正弦,可得三角形ABC的面積為1/2ab sinc;如果過點B作AC的垂線,可得三角形的面積為1/2bc sinA. (l)利用上述的三個結論,試證明sinA - sinB -sinC (2)如圖9,已知三角形ABC中兩個角的度數,即∠B為15°,∠C為60°,且一邊AB的長為20√3,試求AC的長. (3)如圖10,有一塊三角形荒地ABC,在點B處觀察點A時,射線BA的方向為北偏東75°,在點C處觀察點A時,射線CA的方向為北偏西45°,且B、C兩點的距離為18 km,那么三角形ABC的面積是多少?(sin 15°≈ 0.3,sin 120°≈ 0.9,√2≈ 1.4,結果取整數) 三角形的邊角關系還包括三角形的一個外角等于兩個內角的和,但是這兩個內角不能與這外角相鄰,三角形的三邊關系、三角關系及邊角關系始終是我們研究的重點,因為邊與角是三角形最重要的兩類要素,其他圖形問題也要轉化為三角形問題解決,因此,深刻認識三角形的邊角關系,并能運用其邊角關系解答相關問題,是初中生學習幾何應具備的基本素養. (責任編輯 黃桂堅)

