基于光場偏振特性的目標表面漫反射分量獲取技術*

蔡玉棟 韓平麗 劉飛3) 閆明宇 邵曉鵬3)?

1) (西安電子科技大學，西安市計算成像重點實驗室，西安 710071)

2) (西安電子科技大學物理與光電工程學院，西安 710071)

3) (西安電子科技大學，先進光學成像前沿交叉研究中心，西安 710071)

針對三維成像、圖像匹配及模式識別等領域中目標表面鏡面反射光成分影響所導致成像效果受限、特征識別準確度低等問題, 提出一種基于光場偏振特性的目標表面漫反射光分量獲取技術. 該技術通過對反射光場中鏡面反射與漫反射分量的偏振特性進行深入挖掘, 充分利用各分量之間的偏振差異性及彼此獨立性的特點, 建立線性約束模型; 此外, 通過確定線性約束模型的最佳混合系數矩陣, 實現復雜反射光場中對漫反射分量的精確獲取和解譯. 仿真與真實場景數據處理結果表明, 該技術能夠有效地分離復雜光場中的漫反射光分量, 解決了目前三維成像及模式識別技術中對純漫反射條件的依賴, 為被動式遠距離三維成像技術在復雜反射光場中的應用奠定基礎.

1 引 言

目前, 在物體表面三維形貌復原技術及圖像匹配、模式識別技術[1?6]中, 為提升算法普適性, 通常假設探測器所接收到的為完全漫反射光. 然而,由于自然界中的絕大多數物體表面反射光場中鏡面反射分量的存在導致以上技術的重建精度大幅降低. 因此, 全面深入分析反射光場特性, 對無先驗的目標鏡面反射分量與漫反射分量分離技術進行研究, 是一項很有意義又亟待解決的問題.

長期以來, 為了去除反射光場中的鏡面反射分量, 精確獲取漫反射分量, 國內外學者們進行了大量研究. 早在1985 年Shafer[7]基于反射光強度特性提出雙色反射模型來對物體表面鏡面反射光與漫反射光進行有效分離. 隨后Klinker 等[8,9]在RGB顏色空間中進一步深入研究了雙色反射分布模型,得到漫反射像素和鏡面反射像素成斜“T”形分布,并用主成分分析法去除單張彩色圖片中的鏡面反射光. 然而, 受實際物體表面粗糙程度、幾何形狀[10]以及噪聲等原因的影響, 提取到斜“T”形是很困難的, 因此降低了該算法的適用性. Tan 等[11]在把像素點投影到最大亮度-色度空間時發現, 同種顏色只含漫反射的像素點成豎直直線, 含有鏡面反射的呈倒弧形, 于是提出了無鏡面反射(specular-free,SF)圖, 并成功地分離了漫反射分量和鏡面反射分量. Shen 和Zheng[12]與Ren 等[13]在Tan 的基礎上提出改進的SF 圖(modified specular-free, MSF),通過將圖像像素分類成簇, 利用最大光強值和光強范圍值之間的比來計算圖像像素點的鏡面反射含量, 由于具有相同光強度比的像素可能具有不同的漫反射色度, 因此該方法會損失圖像紋理特征.Sato 和Ikeuchi[14]通過在移動光源下采集圖像序列的顏色成分來計算鏡面反射光, 并得到了較好的結果. 但實際成像中光源方向的限制導致該方法的應用大幅受限.

隨著探測技術的成熟, 光場多維物理特性的獲取和解譯能力的提升使得對光波偏振特性的利用得到了長足進步. 與傳統的強度成像技術相比, 偏振成像技術凸顯目標的能力更強, 更具有優勢. 因此Wolff 和Boult[15]在針對面型測量技術中, 引入偏振技術, 將物體表面的反射光成分進行分類, 提出菲涅耳反射模型, 在忽略漫反射部分偏振特性的前提下, 首次利用偏振片實現了黑白圖像中的鏡面反射分量和漫反射分量的分離. Nayar 等[16]改進了這種方法, 將色彩信息和偏振信息結合來對反射光進行分離, 該方法雖然具有較高的算法魯棒性,但對獲取的多個偏振子圖像的每一個像素點進行偏振參數擬合的這一迭代過程卻大幅降低了算法的時效性. Umeyama 及Godin[17]在Wolff 的基礎上, 研究得出漫反射和鏡面反射分量在圖像形成過程中是同時存在的, 通過旋轉偏振片采集多幅高反射率物體表面圖像, 得到采集圖像中含有恒定漫反射分量和不同強度的鏡面分量, 利用漫反射和鏡面反射分量的獨立性構建價值函數, 通過最小化價值函數來分離反射分量. 上述所有基于偏振技術的反射分離方法都建立在漫反射光為完全非偏振光的假設之上, 而由于實際探測時漫反射光具有一定偏振特性[18], 這就導致目前的分離方法的適用性受限.

針對以上問題, 本文提出一種更具普適性的基于光場偏振特性的目標表面漫反射分量獲取技術,在無光源色度、方向及圖像顏色信息等先驗知識的前提下, 充分考慮目標反射光場中漫反射與鏡面反射分量的部分偏振特性, 利用其偏振特性的唯一性及差異性建立線性約束模型, 并求解滿足該約束的最佳分量混合系數, 提取目標表面反射光的漫反射分量. 仿真及真實場景數據處理結果表明, 該分離方法不僅有效地實現了鏡面反射與漫反射的分離,而且具有良好的算法魯棒性.

2 反射光偏振特性分析

由光場傳輸理論可知, 物體表面反射光由于表面粗糙度、反射率等因素的影響, 會產生不同的反射成分. 1991 年Wolff 和Boult[15]在深入分析了物體表面的影響因素后, 結合Fresnel 定律對非朗伯體表面反射光成分進行了詳細的四類劃分, 如圖1 所示. ①光束在遠大于入射光波長尺寸的平面經過單次反射而形成的鏡面反射光; ②光束在物體表面的多個微面元產生多次(≥ 2 次)反射, 然后重新返回到入射介質中的反射光; ③光束在介質界面先進入到物體內部, 通過物體內部微粒之間相互作用后, 最終折射進入到入射介質中的反射光;④光束在遇到尺寸與其入射光波長在同一個量級的細小微小面元而產生的衍射光.

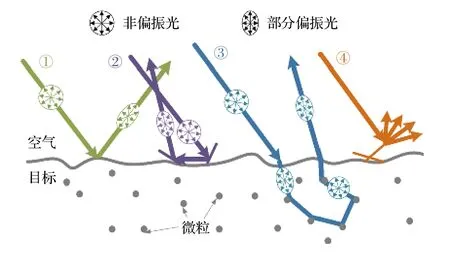
圖1 物體表面反射光分類Fig. 1. Classification of reflected light on the reflection surface.

圖1中①所描述的反射成分, 即通常所說的鏡面反射光, 是在入射光的波長尺寸遠小于物體表面的尺寸時候形成的, 這種光具有極強的方向性, 通常只能在特定的方向才能夠觀察到, 與②中的成分一起, 它們構成人眼看到物體表面的高光部分, 其顏色與光源顏色一致. 對于光滑物體來說, 一次鏡面反射光成分較多, 物體局部反射亮度高, 高光范圍窄; 對于粗糙物體, 多次反射光成分較多, 物體高光部分亮度較低, 高光范圍也較寬. 通常情況下,④中描述的反射光需要物體表面具有波長尺寸量級才會發生, 所以大多數情況下它的存在極少, 可以忽略. ③屬于漫反射光, 反映了物體對入射光的散射和吸收作用, 對于人眼來說, 可以通過它來區分物體的顏色信息, 同時由于它在進入到物體表面之后經過物體內部微粒的散射然后再次折射進入到空氣當中, 帶有物體豐富的表面形狀信息, 而且其方向性沒有鏡面反射強, 探測起來更為方便, 所以經常被選來用作三維形貌復原. 也常被用在諸如圖像分割、圖像識別與匹配等大多數計算機視覺中.

此外, 光在傳播過程中, 在不考慮吸收和色散等能量損耗的情況下, 入射光經過介質表面的反射與折射就只是能量重新劃分的過程, 入射光能量按照一定的比例分別進入到反射光和折射光之中. 由于任意偏振態的光均可以分解為兩個相互垂直的分量, 一般是把它分解成平行入射面的p 分量和垂直于入射面的s 分量. 假設界面上的入射光、反射光和折射光同相位, 則根據菲涅爾定律可知平行和垂直分量的菲涅耳系數如下式所示:

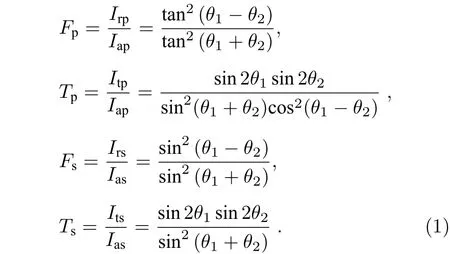
其中Iap,Ias分別是平行于和垂直于入射面的入射光強;Irp,Irs分別是平行于和垂直于入射面的反射光強;Itp,Its分別是平行于和垂直于入射面的透射光強;θ1與θ2分別是入射角及折射角. 當非偏振光照射到物體表面時, 由于菲涅耳系數的差異性導致反射光和透射光均具有一定的偏振特性. 此外, 由Wolff 的反射模型可知, 在入射面上一次或多次反射的鏡面反射光呈現出與入射角相關的部分偏振特性, 同理可知, 漫反射光雖然在物體內部經歷了一次完全退偏過程, 但再經過一次透射回到空氣中時, 具有只和出射面形狀相關的部分偏振特性. 而目前的反射分離方法中為計算簡便, 通常忽略漫反射光的部分偏振特性, 將其視為完全非偏振光進行處理[15?17], 這在一些特定情況下是可行的, 但不具有普適性. 因此, 本文考慮漫反射光的部分偏振特性, 利用其與鏡面反射光彼此獨立的性質, 通過偏振相機采集四幅標準偏振子圖像, 并能夠將反射光光強表示為如下形式:

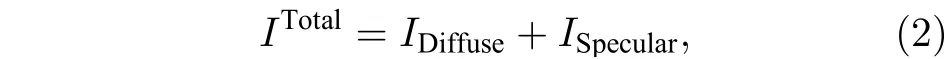
其中ITotal是總光強圖像;IDiffuse和ISpecular分別是目標表面漫反射和鏡面反射強度圖像; 由于鏡面反射與漫反射成份中偏振方向的差異性, 設fd(φi) 和fs(φi) 為相應的調制函數, 均為偏振片旋轉角度φi的函數. 因此, 對于偏振方位角圖像的強度Ii則應為fd(φi)IDiffuse+fs(φi)ISpecular. 而對于完全非偏振光部分, 由于其旋轉偏振片過程中強度的不變性, 強度為最小透射光強Imin的2 倍.

3 漫反射成分獲取模型

通過第2 節對反射光的偏振特性進行分析可知, 探測器接收到的光強是由具有完全偏振特性的漫反射光、鏡面反射光及完全非偏振光三部分組成, 如(2)式所示. 如果不考慮完全非偏振部分, 則經過偏振片后獲得的目標表面反射光強是相互獨立的鏡面反射分量與漫反射分量偏振部分的線性和[7]. 在信號處理領域, 獨立成分分析就是一種用于將多元信號分離為加性子分量的計算方法. 它是在盲信號分離的研究過程中出現的一種新興的、功能強大的非線性數據分析方法, 該方法著眼于數據間的高階統計特性, 其本質是在源信號和混合參數均未知的前提下, 僅依據源信號的一些基本統計特征, 由混合信號恢復出源信號[19?22]. 假設m個隨機觀測向量x1,x2··· ,xm是由n個未知的獨立分量s1,s2··· ,sn線性組合而成的, 則獨立成分分析的數學模型可以表示為

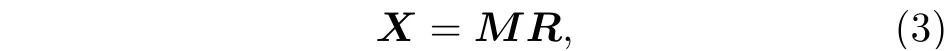
其 中X=[x1,x2··· ,xm], R=[s1,s2··· ,sn] ,M為m×n的混合矩陣,M和R是未知的. 獨立成分分析解決的基本問題就是根據對R的一些先驗知識和隨機觀測向量xi來估計M和R. 據此, 可以利用獨立成分分析的這種架構來對目標表面的反射成分進行分離.

Wolff 在文獻[15]中提到,Imax-Imin的差值表示線性偏振反射光的大小. 最小透射輻射Imin是反射光中的非偏振分量的一半, 可以用Imin來消除(2)式中完全非偏振光成分, 建立鏡面反射分量與漫反射分量的線性約束關系. 考慮到采集有四幅偏振子圖像, 在去除完全非偏振光成分后, 通過行掃描將偏振子圖像矩陣矢量化為行向量xj,j=1,2,3,4, 用新的觀測矩陣X來表示. 同時將鏡面反射分量與漫反射分量在不同偏振角度下得到的線性方程矩陣化, 得到如(4)式所示線性約束模型,其中矩陣M表示所有偏振子圖像對應線性方程組的系數矩陣, 矩陣R對應的兩個元素和分別是矢量化的反射光場中偏振部分的漫反射分量和鏡面反射分量.

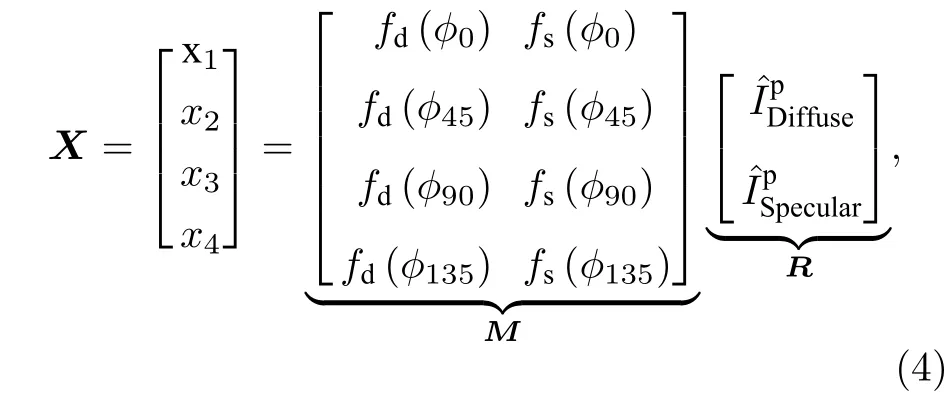
因此, 鏡面反射與漫反射分離的問題就轉化為對線性約束模型中的觀測矩陣X進行最優分解的問題. 在旋轉偏振片采集不同光強圖像時, 漫反射的完全偏振部分的透光軸方向被選作φ0方向, 考慮到鏡面反射光與漫反射光的透光軸不在同一個位置, 根據馬呂斯定律, 矩陣M的第一列元素為fd(φ0)?[1;1/2;0;1/2]. 考 慮到fd(φ0) 是 一個 常 數,它只影響圖像整體的亮暗, 不影響矩陣的分解結果, 為求解方便假設其值為1. 此外, 由于矩陣M和R的秩是2, 所以它們的乘積矩陣的秩也為2.因此, 我們用一個秩為2 且易分解的矩陣來近似X, 并把它按需求分解成兩個矩陣的乘積.

(3)鼓勵企業實行公司制改制，國企混改、民企股改，加快產業轉型升級。把科技創新落實到產業轉型升級上，聚焦新能源新材料等新興產業領域，加快技術引進和創新成果推廣應用，提升產業核心競爭力。

由于矩陣X( 4×n階,n＞4 )是任意的, 把任意矩陣的奇異值按從大到小的順序排列后, 容易發現, 奇異值衰減迅速, 其前10%甚至前1%的奇異值的和已經占了全部奇異值和的99%以上[23?25].據此為了匹配秩為2 這個條件同時減少計算量, 在這里采用奇異值分解(SVD)的方法, 用一個秩較小的矩陣逼近一個矩陣并將其分解為兩個矩陣的乘積. 將X的奇異值分解表示為X4×n=U4×4Σ4×4(VT)4×n, 其 中U是4 × 4 階 酉矩陣;Σ是4 × 4 階非負實數對角矩陣;VT即V的共軛轉置,V是n× 4 階酉矩陣. 引入一個任意的2 × 2非奇異矩陣W矩陣, 則最終期望的分解如下式所示:

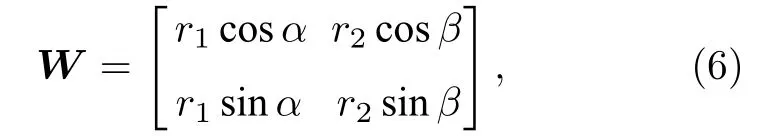
其 中r1和r2都是正實數, 且r1和α的值可以通過M矩陣的第一列元素求得. 同時考慮到W的行列式為?=r1r2sin(β-α),?的絕對值對應于鏡面反射圖像的縮放. 因此, 為了不失一般性令?=1 ,考慮β,r2＞0,逐步改變β∈[0,π] 并利用R=計算漫反射和鏡面反射圖像.為了實現準確分離, 采用互信息MI (mutual information)來衡量漫反射光部分和鏡面反射光部分之間的相關性[26]:

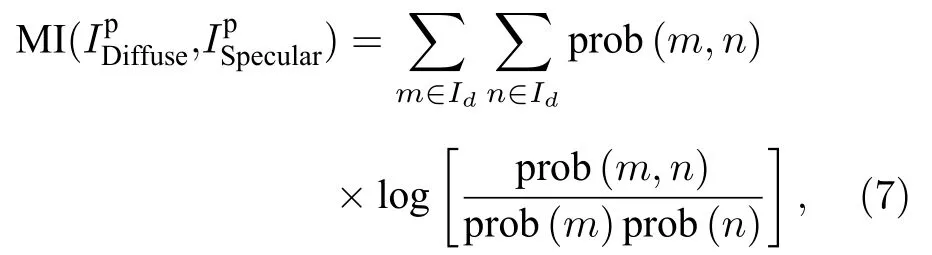
其中m和n分別為漫反射光圖像和鏡面反射光圖像的灰度級; p rob(m,n) 表示聯合概率分布函數; p rob(m) 和 prob(n) 通常為邊緣分布函數. 根據互信息的定義, 當互信息取最小值時, 漫反射和鏡面反射光之間相關性最低, 利用此時得到的W矩陣去求解,R中分離出的漫反射分量將不再包含鏡面反射分量, 然后根據Imin的灰度直方圖分布, 利用鏡面反射光強明顯大于漫反射這一物理規律, 尋找波峰位置所對應最高的灰度級作為閾值, 小于該閾值的光強保持不變, 大于該閾值的光強賦值為該閾值, 得到非偏振部分的漫反射光強值, 結合得到通常意義上的完整漫反射光強值, 最終實現二者的最佳分離效果.

4 實驗結果及分析

為驗證基于光場偏振特性的目標表面漫反射與鏡面反射分離方法的有效性, 根據Lambert 漫反射模型和Torrance-Sparrow 鏡面反射模型分別對實驗仿真得到的人臉數據進行渲染, 得到表面是漫反射光和鏡面反射光的仿真結果如圖2 所示.

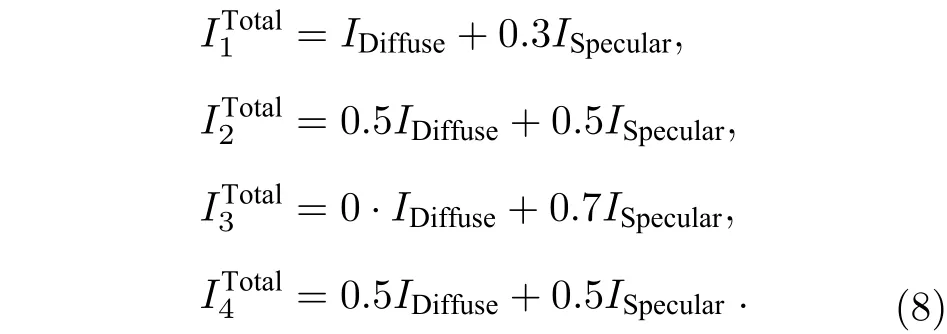
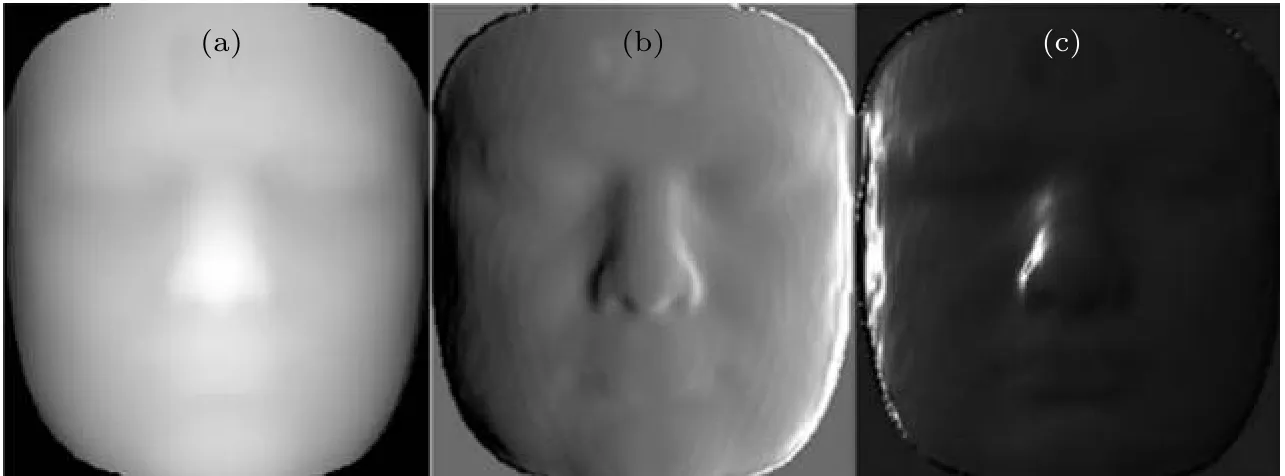
圖2 (a) 仿真人臉深度信息; (b), (c) 通過渲染后的漫反射和鏡面反射仿真圖像Fig. 2. (a) Simulated face depth information ; (b), (c) simulated images with diffuse and specular reflections after rendering,respectively.

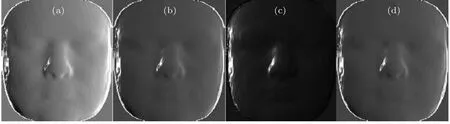
圖3 基于二色反射模型的四幅模擬圖像 (a), (b), (c), (d)分別代表(8)式混合后的光強分布 I 1T otal , I 2T otal , I 3T otal 和I4TotalFig. 3. Four simulated images based on dichromatic reflection model, (a), (b), (c) and (d) represent the intensity image I 1T otal , I 1Total ,I3T otal and I 4Total obtained from Eq. (8), respectively.

此時設定的真實分量混合系數矩陣為

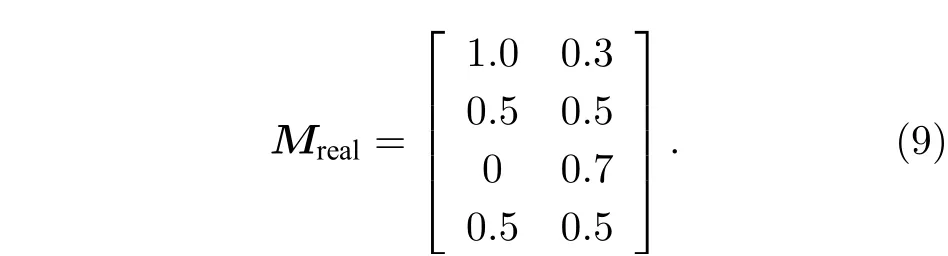
根據第3 節中提出的反射分離算法, 不斷改變β利用(6)式獲取不同的W矩陣來得到不同的分離結果, 利用(7)式計算每次分離后兩個子分量間的互信息結果如圖4 所示, 當β=0.545 rad 取得極小值時鏡面反射與漫反射圖像的相關性最小, 在該條件下求得的W矩陣可以得到最佳分離結果, 此時算法求取的混合系數矩陣M'如(10)式所示, 通過與(9)式真實混合系數做對比可發現, 本文提出的算法有效恢復了仿真圖像的子分量混合系數, 成功提取出了漫反射分量與鏡面反射分量,

在算法分離過程中得到的所有互信息值如圖4所示, 其中圖4(a), (b)分別是互信息在最小處β=0.545 rad 時所得到的漫反射分量與鏡面反射分量的分離結果. 圖4 中隨著β增大到2.4 位置開始, 互信息值出現明顯劇烈的起伏運動, 首先是由于該圖的處理對象是仿真的鏡面反射與漫反射分量隨意組合的結果, 其兩者之間較低的相關性導致縱坐標范圍在0—0.17 之間, 會進一步突顯抖動的劇烈程度. 其次, 在計算互信息(MI)(IDpiffuse,ISppecular)時, 由(7)式可知, 需要統計IDpiffuse和ISppecular圖像中所占每一灰度級像素的個數, 隨著β∈[0,π] 的改變, 將會得到具有不同程度相關的兩幅圖像, 若其中一副圖像部分區域的像素值在原來的基礎上減小1, 也會導致在統計灰度級的個數時, 數目發生明顯遷移, 從而導致位于該灰度級像素的概率發生變化, 進而導致分布函數突變. 該現象在任意一段由β改變所導致圖像灰度級所占像素個數發生明顯遷移的過程中都可能存在, 僅僅與β改變時其每次增加的間隔大小有關系, 但是隨著分離過程的進行, 所獲得的子分量圖像會逐漸接近最獨立的狀態, 互信息度的值總會呈現減小趨勢, 從而達到最優的分離結果, 所以對β最小值的選取是沒有影響的. 這里為了更加準確, 詳盡的反映出β改變時對分離結果的影響, 設定β每次增加量只為0.001 去計算混合系數矩陣得到最終分離結果如圖4 所示.

圖4 互信息隨β 變化情況及鏡面反射和漫反射最終分離結果 (a) 分離的最優漫反射; (b) 分離的最優鏡面反射Fig. 4. Mutual information variation and the finally separated diffuse and specular reflection: (a) The optimal separated diffuse reflection; (b) the optimal separated specular reflection.

為了驗證算法的魯棒性與穩定性, 保持分量混合系數矩陣第一列數值不變, 通過改變第二列中的四個系數進行精度分析, 結果如圖5 所示. 曲線上的圓圈表示鏡面反射分量混合系數所對應的設定值, 菱形表示通過算法獲取到的鏡面反射分量的系數值. 不同顏色的曲線變化是相對獨立的, 代表4 個不同分量混合系數之間沒有關聯性. 同一顏色下每一組測試所對應的兩個點的距離反映了處理效果的魯棒性. 帶有藍色五角星的曲線表示每一組鏡面反射分量設定值組成的向量與算法計算得到的系數組成向量之間的歐氏距離, 其值越小表示算法計算的數值越接近設定值. 對比其他幾組數據來說, 第1 組和第7, 10 組的誤差較大, 分析其原因主要是紫色線所對應的系數3 誤差大導致的. 這是由于在計算時該系數在混合系數矩陣中所對應的漫反射分量系數值為0, 該部分漫反射分量不受約束, 而在利用基于ICA 架構的分離算法去求解時,由于算法不能無限逼近0 值, 漫反射分量無法實現絕對消除, 從而導致系數3 相對于其他三個系數來說誤差大, 但是總體而言其誤差不會超過0.1, 這意味著對最終分離結果影響不大.

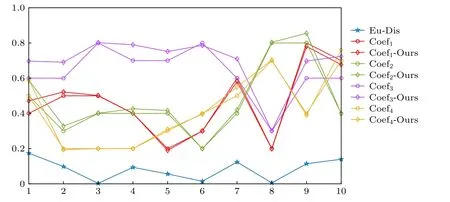
圖5 10 組仿真測試數據圖 Coef1, Coef2, Coef3 和Coef4 是鏡面反射分量混合系數的4 個設定值; Coef1-Ours, Coef2-Ours, Coef3-Ours 和Coef4-Ours 是算法得到的混合系數值; Eu-Dis 表示每組設定值組成的向量跟算法計算值組成的向量之間的歐氏距離Fig. 5. Plots of ten sets of simulation test data: Coef1, Coef2, Coef3 and Coef4 are four set values of the coefficients of the specular reflection components; Coef1-Ours, Coef2-Ours, Coef3-Ours and Coef4-Ours are the coefficients obtained by our algorithm; Eu-Dis represents the Euclidean distance between the vector composed of set values and the vector composed of the calculated values of our algorithm in each group.

考慮到生活中目標的多樣性以及光場環境的復雜性, 利用Thorlab LPVISC100-MP2 線偏振片配合EOS77 D 佳能相機對一個非理想朗伯體陶瓷物體采集偏振子圖像, 利用基于光場偏振特性的目標表面漫反射成分獲取算法對真實場景下的目標進行鏡面反射與漫反射分量分離, 結果如圖6所示.

如圖6(d)所示為偏振片在0°方向下獲取的目標原始光強圖片, 其中高光區域主要是由鏡面反射造成的. 圖6(e)和圖6(f)分別是在互信息最小β=2.46 rad 時, 計算所得的真實場景下的鏡面反射與漫反射分量. 圖6(a), (b), (c)分別是圖6(d), (e), (f)沿圖示紅虛線處的光強梯度分布, 表示每一像素位置處光強值的變化情況. 圖6(a), (c)中300 像素位置附近存在尖峰, 光強梯度值產生突變, 這是鏡面反射光的存在所導致的, 因此在去除鏡面反射后的漫反射分量圖6(b)中, 該位置不再存在梯度的突變. 圖6(h)是圖6(d), (e), (f)沿圖示藍實線位置獲取的光強截面結果, 橫坐標對應像素位置, 縱坐標表示光強值的大小, 由此可見, 總光強是鏡面反射分量跟漫反射分量的線性疊加, 去除鏡面反射后的漫反射分量光強分布符合物體表面形狀的變化趨勢.

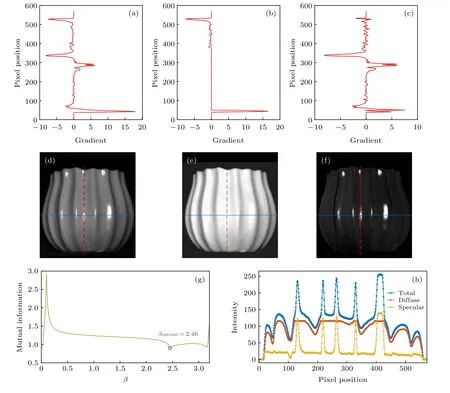
圖6 陶瓷目標表面反射光強分布及分離結果 (a), (b)和(c)分別為圖(d), (e)和(f)沿圖示紅虛線處的光強梯度分布; (d)是偏振片在0°方向下獲取的目標原始光強圖片; (e)和(f)分別是算法處理后最優的漫反射和鏡面反射光強分布; (g)是算法處理過程中得到的互信息圖; (h)是(d), (e), (f)沿圖示藍實線位置的光強截面結果Fig. 6. Intensity distribution and separation results on the surface of ceramic object: (a), (b) and (c) are the light intensity gradient distribution along the red dotted line shown in Fig. (d), (e) and (f), respectively; (d) is the original light intensity of the target obtained from the polarizer at the direction of 0°; (e) and (f) are the optimal light intensity distributions of diffuse and specular component after our algorithm, respectively; (g) is the mutual information plot obtained during algorithm processing; (h) is the results of light intensity cross section obtained along the blue solid line in Fig. (d), (e) and (f).

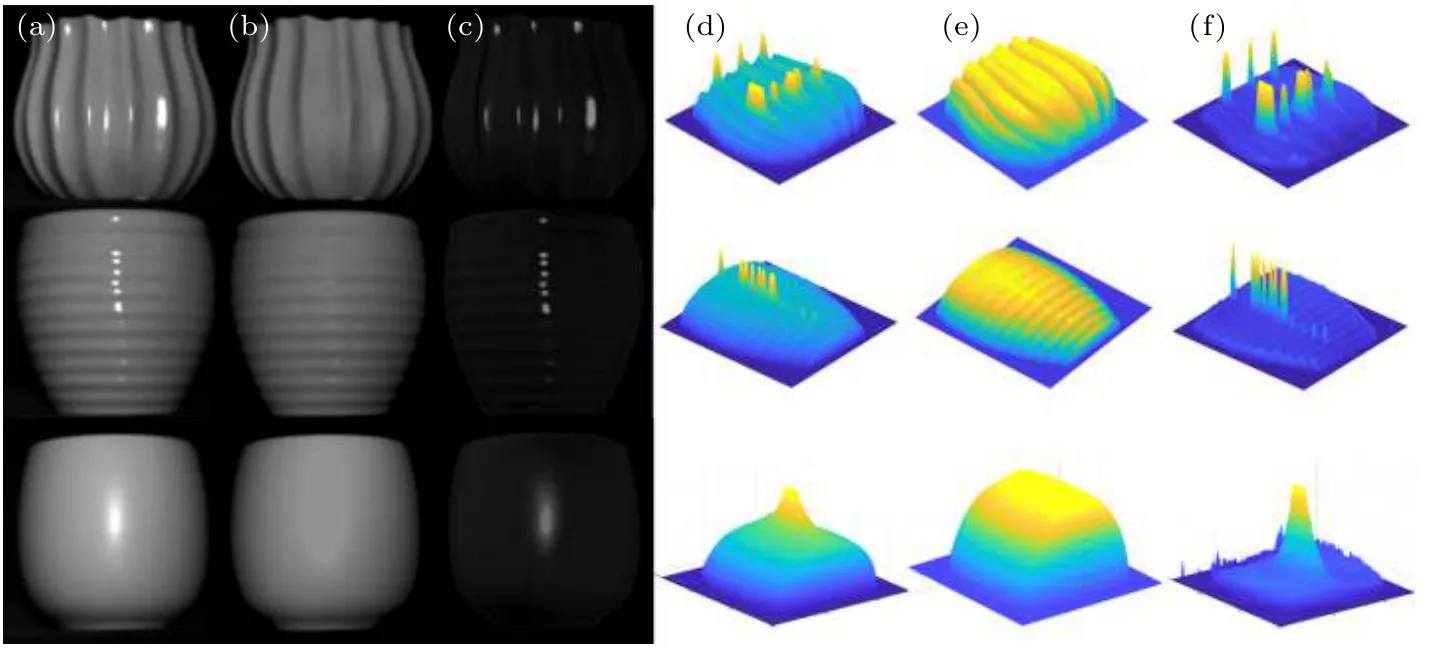
圖7 其他目標反射成分分離結果 (a) 總光強分布; (b), (c) 分離后的漫反射分量和鏡面反射分量光強分布; (d), (e), (f) 分別為(a), (b), (c)的光強空間顯示結果Fig. 7. Reflection separation of three different objects: (a) Total light intensity distribution; (b), (c) light intensity distributions of separated diffuse and specular reflection, respectively; (d), (e), (f) spatial display of (a), (b) and (c) respectively.

為表征算法的普適性,本文還對其他表面紋理單一和表面紋理復雜物體的三種非朗伯體目標進行了實驗,結果如圖7 所示.圖7(b)和圖7(c)分別表示在各自對應互信息取得最小值時,所得的分離后最優的漫反射分量跟鏡面反射分量,圖7(e)和圖7(f)是它們各光強分布的空間展示結果.由此可見,對于各類具有非理想朗伯體表面的物體,在考慮漫反射跟鏡面反射所具有的部分偏振特性后,仍然能夠有效地將疊加到一起的鏡面反射分量跟漫反射分量進行分離,同時在鏡面反射高光區域內成功地恢復出了物體表面的形狀等細節信息,客觀表明了基于光場偏振特性的目標表面漫反射分量獲取技術的普適性.

5 結 論

針對三維重建、圖像匹配及模式識別等技術中目標表面反射光復雜的問題,提出了基于光場偏振特性的目標表面漫反射分量獲取技術.深入挖掘漫反射分量和鏡面反射分量的部分偏振特性,利用二者的差異和互相獨立的特點,建立線性約束模型;采用奇異值分解方法求解其最佳混合系數矩陣,從而實現了從復雜反射光場中對漫反射分量的精確獲取和解譯.仿真結果表明,該算法能夠在無光源色度、方向及圖像顏色信息等先驗知識的前提下準確計算最佳混合系數矩陣,具有較好的分離效果穩定性與普適性.此外,實驗結果證明了該算法不僅能夠實現對鏡面反射區域的精準獲取,而且能夠恢復出被鏡面反射光所覆蓋掉的符合物體表面形狀變化趨勢的漫反射光強值.該技術能夠在圖像分割、特征匹配以及模式識別等計算機視覺算法中,移除鏡面反射強光的干擾,凸顯物體表面的形狀紋理等特征,克服復雜反射光場對目標結果的影響.同時由于該技術在進行反射分離時保留了漫反射分量所具有的偏振特性,提高了偏振探測方法的適用性.