涂覆石墨烯的非對稱橢圓電介質納米并行線的模式分析*

董慧瑩 秦曉茹 薛文瑞? 程鑫 李寧 李昌勇

1) (山西大學物理電子工程學院, 太原 030006)

2) (山西大學激光光譜研究所, 量子光學與光量子器件國家重點實驗室, 太原 030006)

3) (山西大學, 極端光學協同創新中心, 太原 030006)

設計了一種涂覆石墨烯的非對稱橢圓電介質納米并行線波導. 在橢圓柱坐標系中, 借助于Mathieu 函數和坐標變換, 采用多極方法對波導所支持的6 個最低階模式進行了研究, 并分析了這些模式的特性與工作波長、石墨烯費米能以及波導結構參數之間的依賴關系. 結果表明, 調節波導的工作波長、石墨烯的費米能及納米線之間的間距, 可大幅度調節這些模式的特性. 調節納米線的半長軸及半短軸, 可以微調這些模式的特性. 在兩種條件下, 通過比較涂覆石墨烯的單根橢圓電介質納米線、對稱橢圓電介質納米并行線與非對稱橢圓電介質納米并行線所支持的基模的性能, 發現本文所設計的波導的性能優于其他兩種波導. 本文的研究工作可以為涂覆石墨烯的非對稱橢圓電介質納米并行線波導的設計、制作及應用提供理論基礎.

1 引 言

石墨烯是單層碳原子以蜂窩狀晶格方式排列而成的一種新型二維結構材料[1?3]. 自2004 年成功制備單層石墨烯以來, 其在雷達吸收表面[4]、微型傳感器[5]、電磁能量轉換[6]、電磁干擾屏蔽[7]等領域引發了很多研究人員的關注. 在THz 波段, 石墨烯的表面電導率幾乎是一個純虛數[8], 與金屬極為相似, 可以支持表面等離子激元, 且相較于金屬而言, 石墨烯中較低的載流子濃度[9]和較高的遷移率[10]更能保證其具有理想的導電性.

表面等離子激元是一種沿著導體表面傳播的電磁波, 由導體表面振蕩的自由電子與電磁場之間的共振相互作用形成, 可以用來在亞波長結構中聚焦和導引光[11]. 研究發現, 基于貴重金屬材料的波導結構中[12?15]可以支持表面等離子激元的傳播.但是這些波導的工作波長大多集中于可見光波段,在中紅外到太赫茲波段內, 波導對場的束縛能力明顯變弱[16]; 且基于貴重金屬的表面等離子波導只能通過變更結構參數來改善其導波特性. 在特定條件下, 石墨烯的光學性質類似于貴重金屬[17], 且與基于貴重金屬的波導相比, 石墨烯波導具有三大優勢: 較低的損耗、極強的模式束縛性及可調的化學勢[18]. 利用石墨烯表面支持的表面等離子激元可以在亞波長范圍內對光波進行操控[19]. 這也為波導在中紅外到太赫茲波段內實現高性能有效傳輸提供了一個新的研究方向. 若在電介質波導表面涂覆單層石墨烯, 可以構成一種傳輸特性良好的表面等離子體波導[20?32].

若在圓形介質納米線表面涂覆單層石墨烯,可改善波導性能[20]; 若在中空的二氧化硅管中嵌入實心硅棒后涂覆單層石墨烯, 可進一步壓縮模式面積、增加其傳播長度[22]; 若將多個外表面涂覆單層石墨烯的中空電介質管緊密嵌套, 可實現極強的模式束縛性[25]; 若將兩根完全一致的涂覆石墨烯的電介質納米線以一定間距置于同一軸線上, 可實現較強的梯度力和場增強[28]. 若在涂覆石墨烯的圓形并行納米線對的中心軸線上放置一圓形納米線, 可以實現較為理想的傳播長度[29];若將兩根完全相同的涂覆雙層石墨烯的電介質納米線間隔一定距離置于同一軸線上, 可實現極強的場增強效應[30]; 若在橢圓介質納米線表面涂覆單層石墨烯, 可實現較長的傳播長度及更強的模式束縛性[31].

本文設計了一種涂覆石墨烯的非對稱橢圓電介質納米并行線波導, 對波導的6 個最低階模式進行了命名和分類, 使用多極方法[33,34]研究了波導的工作波長、石墨烯的費米能以及波導的結構參數對6 個最低階模式的模式特性的影響, 并比較了兩種條件下3 種波導結構的傳輸性能. 本文的研究結果有望在模式轉換[35]及耦合器件[36]中得到應用.

2 結構模型和計算方法

涂覆石墨烯的非對稱橢圓電介質納米并行線波導結構的橫截面如圖1 所示, 它由兩根結構參數不同的涂覆單層石墨烯的并行橢圓形電介質納米線構成, 背景為空氣. 將左右兩根納米線分別標記為1 號納米線和2 號納米線. 以1 號納米線的對稱中心o1為原點, 建立直角坐標系o1-xy和橢圓坐標系o1-ξ1η1; 以2 號納米線的對稱中心o2為原點, 建立直角坐標系o2-x2y2和橢圓坐標系o2-ξ2η2; 以o1和o2連線的中點o為原點, 建立直角坐標系o-xy.橫截面內的任意一點在五套坐標系中的坐標分別為(x1,y1),(ξ1,η1) ,(x2,y2) ,(ξ2,η2)和(x,y) . 坐標之間的關系為x1=x+c,x2=x-c,y1=y2=y,x1=q1coshξ1cosη1,y1=q1sinhξ1sinη1,x2=q2coshξ2cosη2,y2=q2sinhξ2sinη2. 其中a1,b1和a2,b2分別為1 號和2 號納米線的半長軸和半短軸,2c為1 號2 號納米線的中心間距,d=2c-a1-a2為1 號和2 號納米線的表面間距.q1,q2分別為1 號和2 號納米線的半焦距,ξ1和ξ2為徑向坐標變量,η1和η2為角向坐標變量. 在兩套橢圓坐標系下, 1 號和2 號納米線邊界處的徑向坐標分別為ξ10和ξ20.

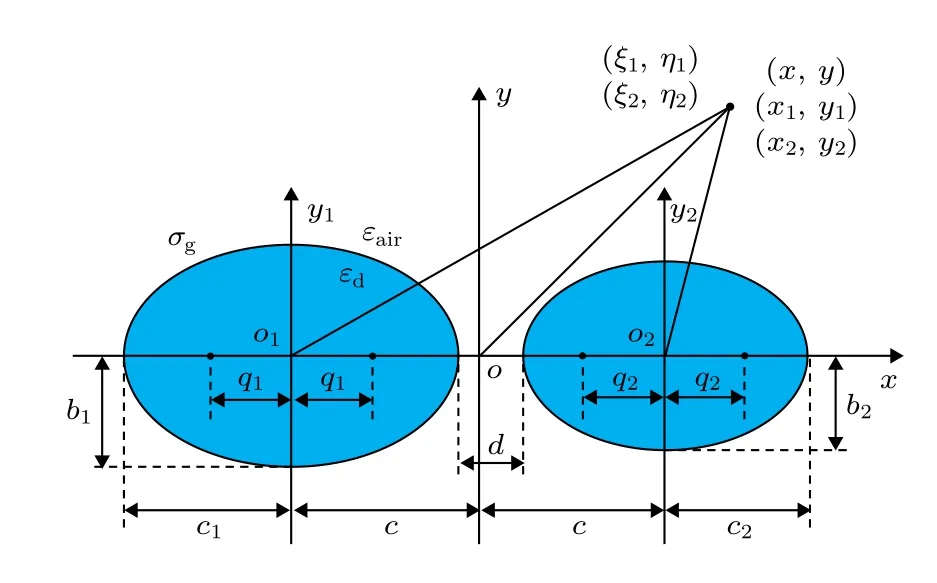
圖1 涂覆石墨烯的非對稱橢圓電介質納米并行線波導的橫截面示意圖Fig. 1. The cross section of the double elliptical nano-parallel wires waveguide coated with graphene.

圖1中εd為電介質的介電常數, 數值為2.1025,對應于石英玻璃材料SiO2.εair為空氣的介電常數,數值為1.0.σg為石墨烯電導率, 其值由兩部分構成:帶內電導率σintra和帶間電導率σinter, 即σg=σintra+σinter, 其表達式由庫珀公式[37]給出:

式中e為電子電量,kB為玻爾茲曼常數,T=300 K為環境溫度, ? 為約化普朗克常量,ω=2πf是角頻率,Γ=2×1012rad/s 是載流子散射率,Ef為石墨烯的費米能, 為了盡可能準確反映石墨烯實際傳輸損耗, 在模擬和計算中將Ef設置為 0.5 eV[8].

采用多極方法, 假設1 號納米線單獨存在時,其內部電場和磁場的z分量為Ez11和Hz11, 外部電場和磁場的z分量為Ez12和Hz12, 它們的表達式為:

設2 號納米線單獨存在時, 內部電場和磁場的z分量為Ez21和Hz21, 外部電場和磁場的z分量為Ez22和Hz22, 它們的表達式為:

其 中,Am,Bm,Cm,Dm,Em,Fm,Gm,Hm,和為 第m階表達式的系數, 共16 組.為第m階第一類徑向Mathieu 偶函數,為第m階第一類徑向Mathieu 奇函數,為第m階第三類徑向Mathieu偶函數,為第m階第三類徑向Mathieu 奇函數,Sem為第m階角向Mathieu 偶函數,Som為第m階角向Mathieu 奇函數[38].ε0為真空介電常數,μ0為真空磁導率.

當1 號和2 號納米線同時存在時, 在弱耦合的條件下, 根據場的疊加原理, 在1 號納米線內部,電場和磁場的z分量為:

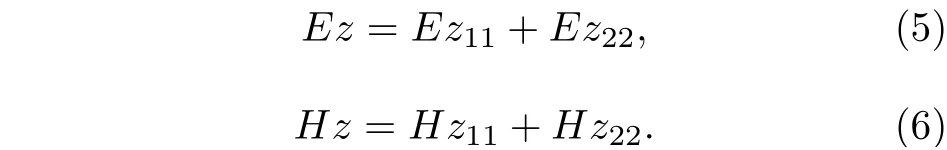
在2 號納米線內部, 電場和磁場的z分量為:

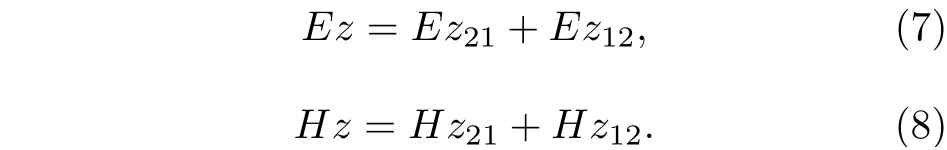
在1 號和2 號納米線外部, 電場和磁場的z分量為:

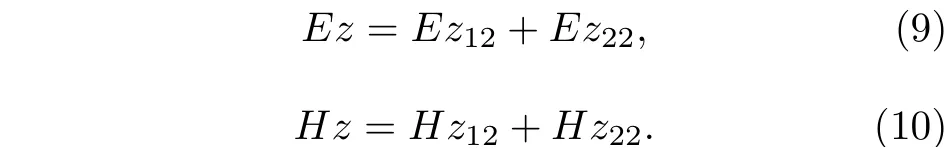
將(5)式—(10)式代入橢圓坐標系下場的橫向分量與縱向分量的關系式(11)式中, 就可以得到各區域內的電場和磁場的徑向和角向分量:

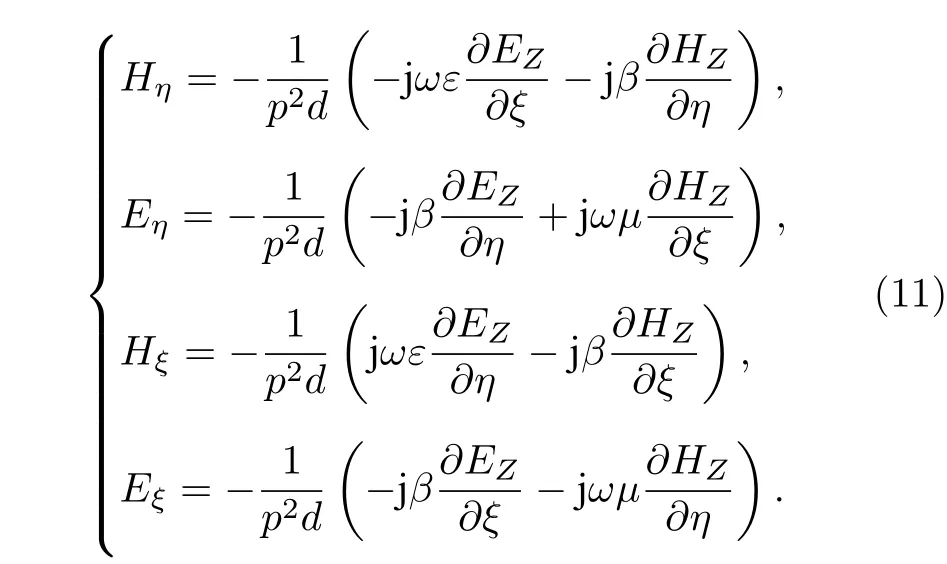
計算中, 所涉及的導數, 可以通過下面4 個式子來解決[39,40]:

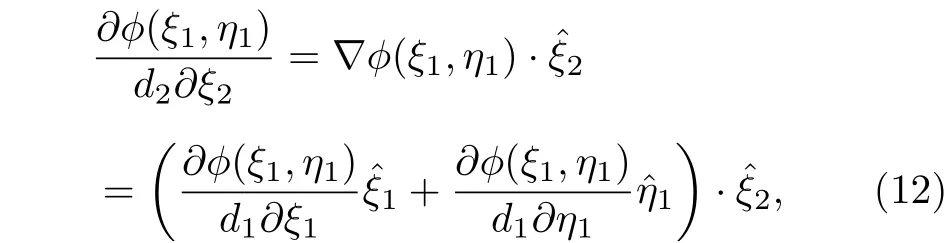
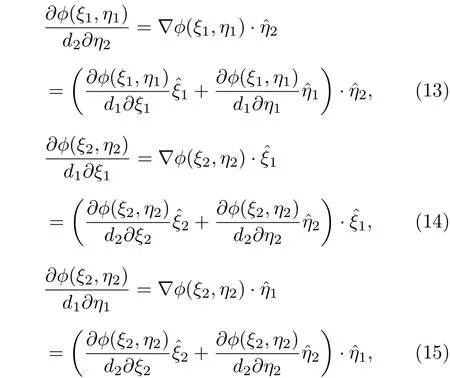
其中φ代表徑向Mathieu 函數與角向Mathieu函數的乘積, 例如和

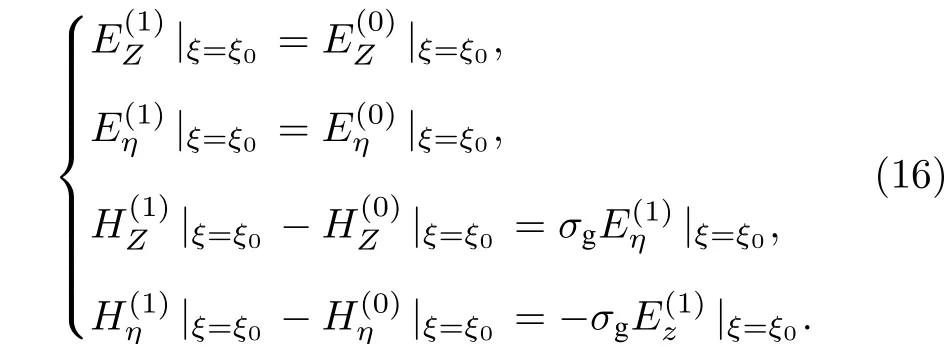
把1 號和2 號納米線表面涂覆的石墨烯看成具有表面電導率為σg的無厚度的界面, 采用逐點匹配方法, 在此界面上應用切向分量之間的邊值關系(16)式, 將得一個線性代數方程組. 按照線性代數理論, 其系數矩陣的行列式(17)式為零時, 才能得到非零解.

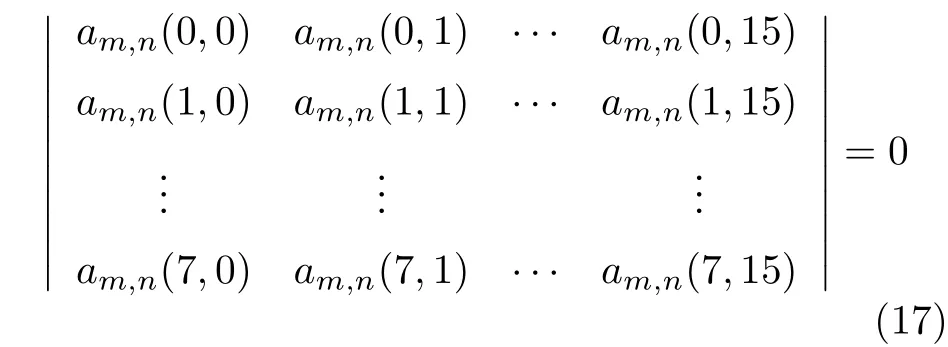
系數矩陣中包含 8×16 個子矩陣. 受篇幅限制, 這里只給出第一個子矩陣的元素表達式:

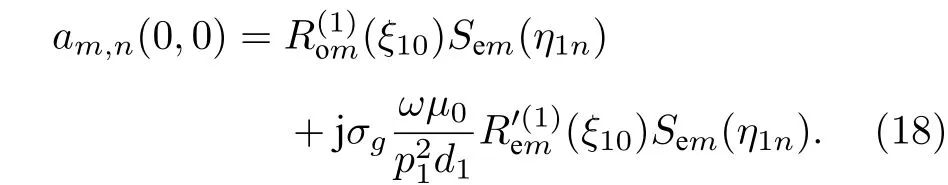
通過數值求解方程(17)式, 就可以得到波導中傳播的模式的場分布、對應的有效折射率以及品質因數. 其中, 有效折射率的實部Re(neff) 直接與波導色散相關, 虛部 I m(neff) 則與衰減有關[41]. 傳播長度由公式Lprop=λ/[4πIm(neff)][42]來定義. 品質因數由 F OM=Re(neff)/Im(neff)[43]給出, 它能夠綜合地表征波導的傳輸性能.

3 結果與討論

3.1 模式分類

圖2 給出了在Ef=0.5 eV ,λ=7 μm,a1=90 nm ,b1=70 nm ,a2=80 nm ,b2=60 nm ,d=40 nm條件下, 涂覆石墨烯的非對稱橢圓電介質納米并行線波導所支持的6 個最低階模式的合成圖、電場的z分量分布圖及電場強度分布圖. 其中,圖2(a)—圖2(f)為模式合成圖, 圖2(g)—圖2(l)為電場z分量分布圖, 圖2(m)—圖2(r)為電場強度分布圖. 可以看出, Mode 0 的場分布集中在兩根納米線之間的間隙區域. Mode 1 的場主要分布在1 號納米線的左側. Mode 2 和Mode 3 的場分布主要分布在兩根納米線的上方和下方, 基本保持了兩根納米線單獨存在時場的特點. Mode 4 的場主要分布在2 號納米線的右側. Mode 5 的場在兩根納米線之間的間隙區域和外側區域的分布均較強. Mode 0 和Mode 1 為1 階模, Mode 2—Mode 5為2 階模.

3.2 模式特性的影響因素

在Ef=0.5 eV 時, 設置波導的結構參數為a1=90 nm ,b1=70 nm ,a2=80 nm ,b2=60 nm ,d=20 nm , 有效折射率實部 Re(neff) 、傳播長度Lprop及品質因數FOM 隨工作波長λ的變化關系如圖3(a),(b),(c)所示.

當工作 波 長λ由 6.2 μm 逐步增加到 7.8 μm 時,6 個最低階模式的有效折射率的實部單調減小, 波導對場的束縛能力減弱, 場分布范圍變大, 場與石墨烯之間的相互作用減弱, 傳輸損耗減小, 傳播長度變長, 但此過程中始終維持Mode 0 的FOM 最大; 當工作波長由 6.2 μm 變化到 7.8 μm 時, Mode 0的有效折射率的實部最大, 傳播長度最長; Mode 5的有效折射率的實部最小, 傳播長度最小; 圖3(d),(e),(f)分別為λ=6.2 , 7 和 7.8 μm 時基模的電場強度變化圖. 當λ=6.2 μm 時, 電場被緊緊地束縛于石墨烯層附近, 此時, 電場強度分布較弱, 波導對場的束縛能力最強, 損耗最大, 傳播長度最小; 當λ=7 μm時, 場分布范圍擴大, 強度變大, 場與石墨烯之間的作用減弱, 損耗變小, 傳播長度增加;當λ=7.8 μm 時, 場與石墨烯之間的相互作用最弱,場分布范圍進一步擴大, 參數變化范圍內, 場分布強度最大, 波導整體損耗最小, 傳播長度最長. 本文所有曲線圖中的實心點均為多極方法得到的結果, 實線均為有限元法得到的結果, 兩種方法得到的結果完全一致, 驗證了多極方法的正確性. 使用有限元法(COMSOL 5.1)進行數值模擬時, 也將石墨烯看作是具有表面電導率σg的無厚度界面.根據歐姆定律, 設置界面處的面電流密度Js=σgE即可.

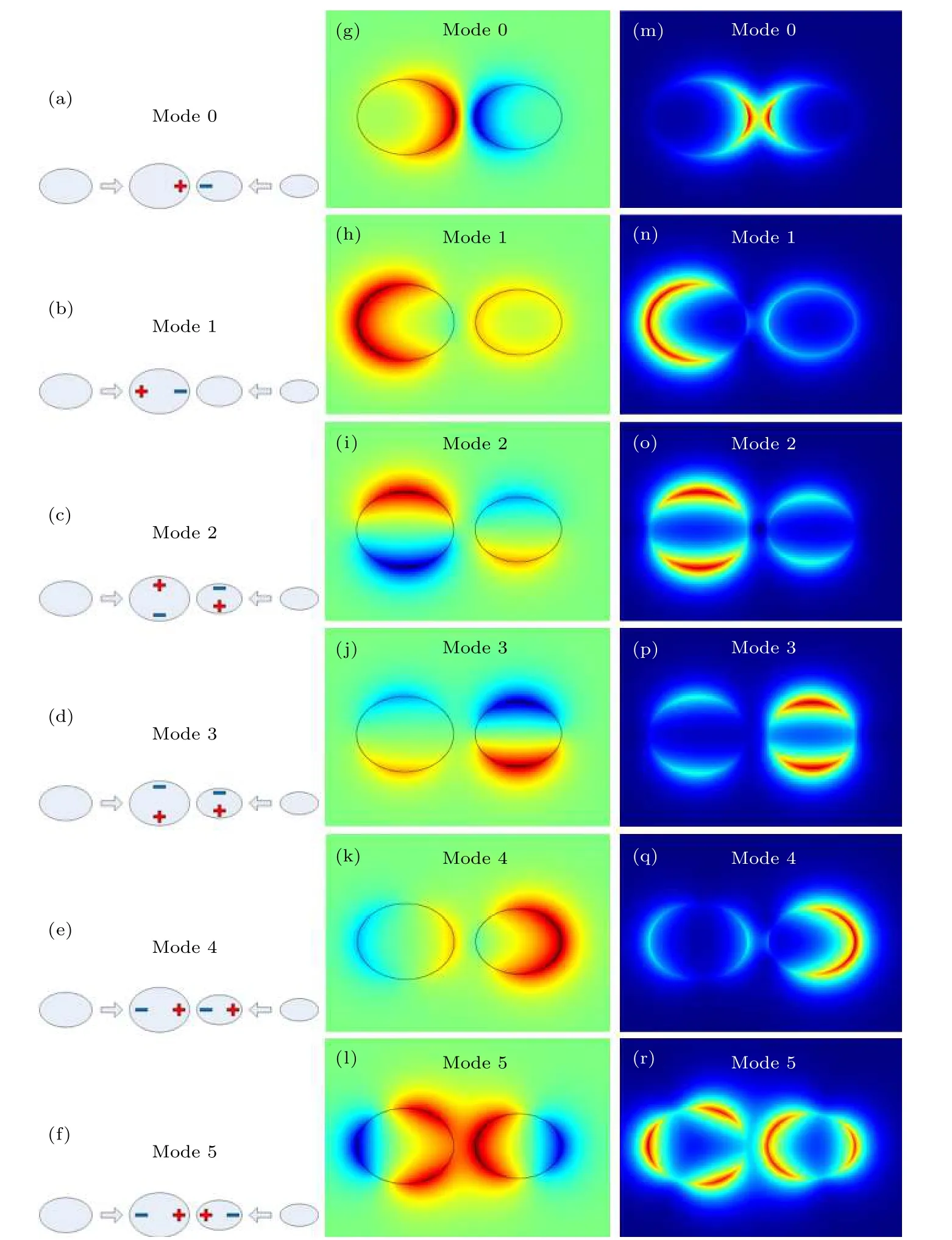
圖2 在E f =0.5 eV, λ=7μm, a 1 =90 nm, b1 =70nm, a2 =80nm, b 2 =60 nm,d=40 nm 條件下, 6 個最低階模式的模式合成圖(a)?(f)、電場的z分量分布圖(g)?(l)和電場強度分布圖(m)?(r)Fig. 2. Ef=0.5 eV , λ=7 μm, a1 =90nm, b1 =70nm, a2 =80nm, b2 =60 nm and d=40 nm, pattern composition diagram (a)?(f), the z-component of electric field Ez (g)?(l) and the electric field distribution |E| for the six lowest order modes(m)?(r).

設置波導的結構參數為a1=90 nm ,b1=70 nm ,a2=80 nm ,b2=60 nm ,d=20 nm ,改 變石墨烯的費米能級Ef, 有效折射率實部 Re(neff) 、傳播長度Lprop及品質因數FOM 隨Ef在λ=7 μm處的變化關系如圖4(a),(b),(c)所示. 當Ef從0.44 eV 向 0.60 eV 變化過程中, 波導支持的6 個最低階模式的有效折射率實部變小, 場與石墨烯之間的相互作用由強變弱, 波導對場的束縛能力逐漸變弱, 損耗減小, 傳播長度增大; 至0.60 eV時, 場與石墨烯之間的作用最弱, 傳播長度最大.在石墨烯的費米能變化過程中, 各個模式的有效折射率實部及傳播長度之間始終保持較為穩定的間 距 差; Mode 0 始 終 以 較 高 的FOM 優 于 其 他模式.

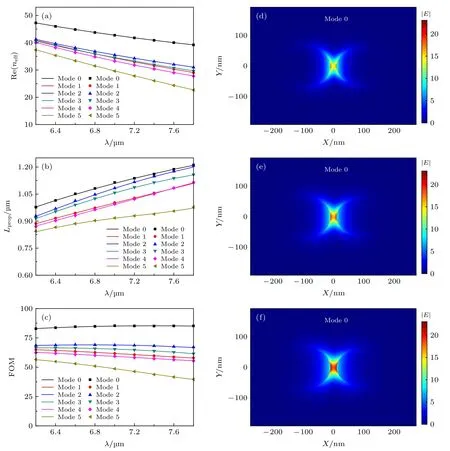
圖3 當 E f =0.5 eV , a 1 =90 nm , b 1 =70 nm , a 2 =80 nm , b 2 =60 nm,d=20 nm 時, (a)有 效 折 射率 Re(neff) 、(b)傳 播 長度 L prop 、(c)品質因數FOM 隨工作波長 λ 變化關系圖; (d) λ=6.2 μm , (e) λ=7 μm , (f) λ=7.8 μm 時基模的電場強度變化圖Fig. 3. The dependence of (a) the effective refractive index Re(neff),(b) the propagation length L prop , (c) the quality factor FOM for the six lowest order modes on the wavelength λ at E f =0.5 eV , a 1 =90 nm , b 1 =70 nm,a 2 =80 nm , b 2 =60 nm ,d=20 nm . And the electric field distribution | E| for (d) λ=6.2 μm,(e) λ=7 μm , (f) λ=7.8 μm .

令結構參數a1=90 nm ,b1=70 nm ,a2=80 nm ,b2=60 nm , 當Ef=0.5 eV 時, 有 效 折 射 率 實 部Re(neff) 、傳播長度Lprop及品質因數FOM 在λ=7 μm處隨兩納米線間距d的變化關系如圖5(a),(b),(c)所示. 逐漸增加兩根納米線之間的距離,Mode 0 和Mode 2 的有效折射率實部下降, Mode 3的有效折射率實部略有增加, Mode 1, Mode 4 的有效折射率實部并無明顯變化; 當兩納米線間距由15 nm 增至 3 5 nm 時, Mode 0 的傳播長度達到最長,繼續增大兩納米線之間的距離, Mode 0 的傳播長度減小; 隨著兩納米線間距不斷增大, Mode 2 的傳播長度變小, Mode 5 的傳播長度增加, 其他模式傳播長度無明顯改變. 結果表明, 增大兩納米線間距, Mode 0, Mode 2 的傳輸性能下降, Mode 5的傳輸性能得以改善; 其余幾個模式對納米線間距這一參數變化并不敏感.

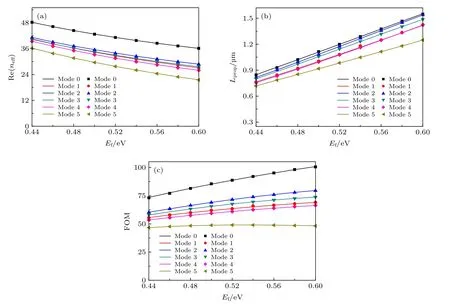
圖4 當 λ=7 μm , a 1 =90 nm , b 1 =70 nm,a 2 = 8 0 nm , b 2 =60 nm,d=20 nm 時 (a)有效折射率 Re(neff) 、(b)傳播 長度Lprop 和(c)品質因數FOM 隨石墨烯費米能 Ef 變化關系圖Fig. 4. The dependence of (a) the effective refractive index Re(neff),(b) the propagation length L prop and (c) the quality factor FOM for the six lowest order modes on the graphene Fermi levels E f at λ=7 μm , a 1 =90 nm,b 1 =70 nm,a 2 =80 nm ,b2 =60 nm , d=20 nm .

以基模為例, 分析調節兩納米線距離時電場分布變化: 當d=15 nm 時, 電場在兩納米線靠近部分呈現反對稱分布, 電場強度最大, 耦合作用較強,傳播損耗較大, 傳播長度最小; 進一步增加納米線間距至 3 5 nm 時, 電場強度變弱, 兩納米線之間的耦合作用減弱, 此時損耗變小, 傳播長度增加; 當d=55 nm時, 兩納米線之間的耦合作用最弱, 波導整體損耗增加, 傳播長度下降, 兩根納米線上的場分布趨向于單根納米線單獨存在時的場分布; 可以推斷, 若兩納米線之間的距離增大至某一特定數值, 兩納米線之間的耦合作用將完全消失, 此時,兩根納米線上的場分布將呈現單根納米線單獨存在時的特點.

在λ=7 μm,Ef=0.5 eV 時, 保持結構參數b1=70 nm ,a2=80 nm ,b2=60 nm ,d=30 nm 不變, 有效折射率實部 Re(neff)、傳播長度Lprop及品質因數FOM 隨a1的變化關系如圖6(a),(b),(c)所示. 當1 號納米線的半長軸由 7 3 nm 增加至97 nm時, Mode 0 有效折射率實部略有下降, Mode 1 和Mode 4 有效折射率實部基本保持不變, Mode 2和Mode 3 有效折射率實部緩慢上升; 隨著a1的逐漸增加, Mode 0, Mode 2, Mode 4 的傳播長度基本保持不變, Mode 3 的傳播長度緩慢增加, Mode 1的傳播長度略有減小; 在所選參數變換范圍內, Mode 0的品質因數最高, 性能最佳, 其余模式的FOM 按照Mode 2, Mode 3, Mode 1, Mode 4 的順序降低.

在λ=7 μm,Ef=0.5 eV 時,保持結構參數a1=90 nm ,a2=80 nm ,b2=60 nm ,d=35 nm , 改變1 號納米線的半短軸長度b1,有效折射率實部 Re(neff) 、傳播長度Lprop及品質因數FOM 隨b1的變化關系如圖7(a),(b),(c)所示. 逐漸將1 號納米線半短軸長由 6 1nm 增加至 85 nm , Mode 0, Mode 1, Mode 5的有效折射率實部明顯增加, Mode 2 的有效折射率實部略有下降, Mode 3 和Mode 4 的有效折射率實部無明顯變化; 同時, Mode 0 的傳播長度基本不變, Mode 2, Mode 3, Mode 4 的傳播長度略有下降, Mode 1 和Mode 5 的傳播長度緩慢增加;在參數所選變化范圍內, Mode 0 的傳輸性能最好.

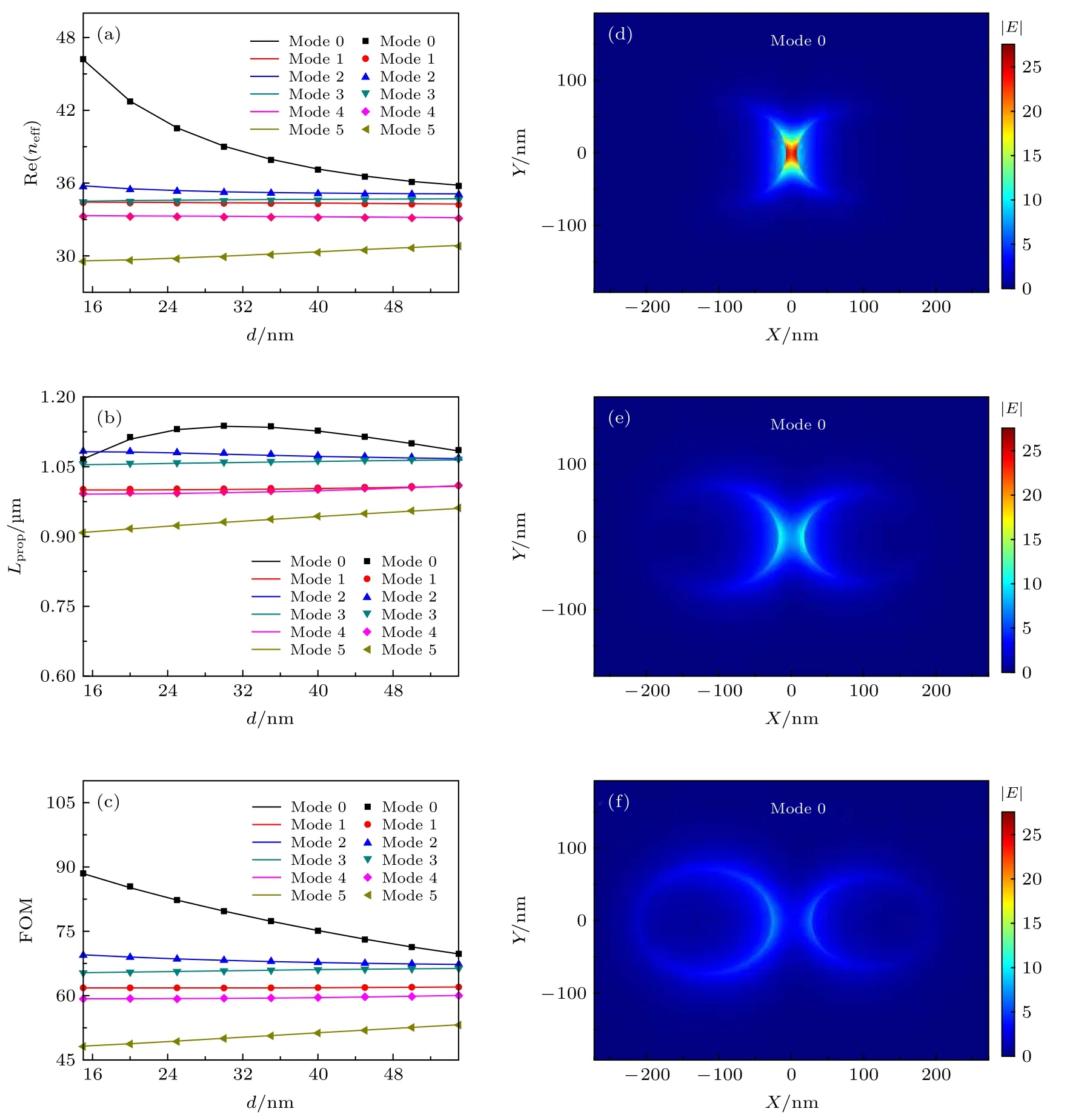
圖5 當 λ=7 μm , E f =0.5 eV , a 1 =90 nm,b 1 =70 nm , a 2 =80 nm , b 2 =60 nm (a)有效折射率 Re(neff) , (b)傳 播 長 度Lprop , (c)品質因數FOM 隨兩納米線間距d 變化關系圖; (d) d=15 nm , (e) d=35 nm , (f) d=55 nm 時基模的電場強度變化圖Fig. 5. The dependence of (a) the effective refractive index Re(neff),(b) the propagation length L prop , (c) the quality factor FOM for the six lowest order modes on the distance d between two nanowires at λ=7 μm , E f =0.5 eV , a 1 =90 nm , b 1 =70 nm ,a2 =80 nm , b 2 =60 nm ; the electric field distribution | E| for (d) d=15 nm , (e) d=35 nm , (f) d=55 nm .

3.3 與其他兩種波導的比較分析

為了說明涂覆石墨烯的非對稱橢圓電介質納米并行線(結構1)的傳輸性能的優越性, 以基模為例, 在兩種條件下, 與涂覆石墨烯的單根橢圓電介質納米線(結構2)和涂覆石墨烯的對稱橢圓電介質并行納米線(結構3)的傳輸性能進行了對比.

設置波導的費米能為Ef=0.5 eV , 假設結構1 的 參 數 為a1=90 nm ,b1=85 nm ,a2=80 nm ,b2=60 nm ,d=40 nm ; 結構2 的結構參數為a2=80 nm ,b2=60 nm ; 結 構3 的 參 數 為a1=a2=80 nm ,b1=b2=60 nm ,d=40 nm . 改變工作波長, 三種結構的有效折射率實部、傳播長度及品質因數如圖8(a),(b),(c)所示, 當工作波長由5.0 μm增加至 6.8 μm 時, 三種波導所支持的基模的有效折射率實部均減小, 傳播長度及FOM 增大. 可以看出, 本文所討論的結構1 的傳輸性能優于其他兩種波導結構.

圖6 當λ=7 μm , E f =0.5 eV , b 1 =70 nm,a 2 =80 nm ,b2 =60 nm , d=30 nm 時, (a)有效折射率實部 Re(neff) 、(b)傳播長度 L prop 和(c)品質因數FOM 隨1 號納米線半長軸 a 1 變化關系圖Fig. 6. When λ=7 μm , E f =0.5 eV , b 1 =70 nm , a2 =80 nm , b 2 =60 nm,d=30 nm , the dependence of (a) the effective refractive index Re(neff) , (b) the propagation length L prop , and (c) the quality factor FOM for the six lowest order modes on the length of a1 on the No.1 nanowire.

在上述結構參數下, 設置石墨烯的工作波長λ=7 μm, 改變石墨烯的費米能, 三種結構所支持的基模的有效折射率實部, 傳播長度及品質因數變化如圖9(a),(b),(c)所示. 可以看出, 當石墨烯的費米能級由 0.39 eV 增加至 0.53 eV 時, 三種波導所支持的基模的有效折射率實部都呈現下降趨勢, 傳播長度及FOM 都逐漸增大. 可以看出, 本文所討論的結構1 的傳輸性能優于其他兩種波導結構.

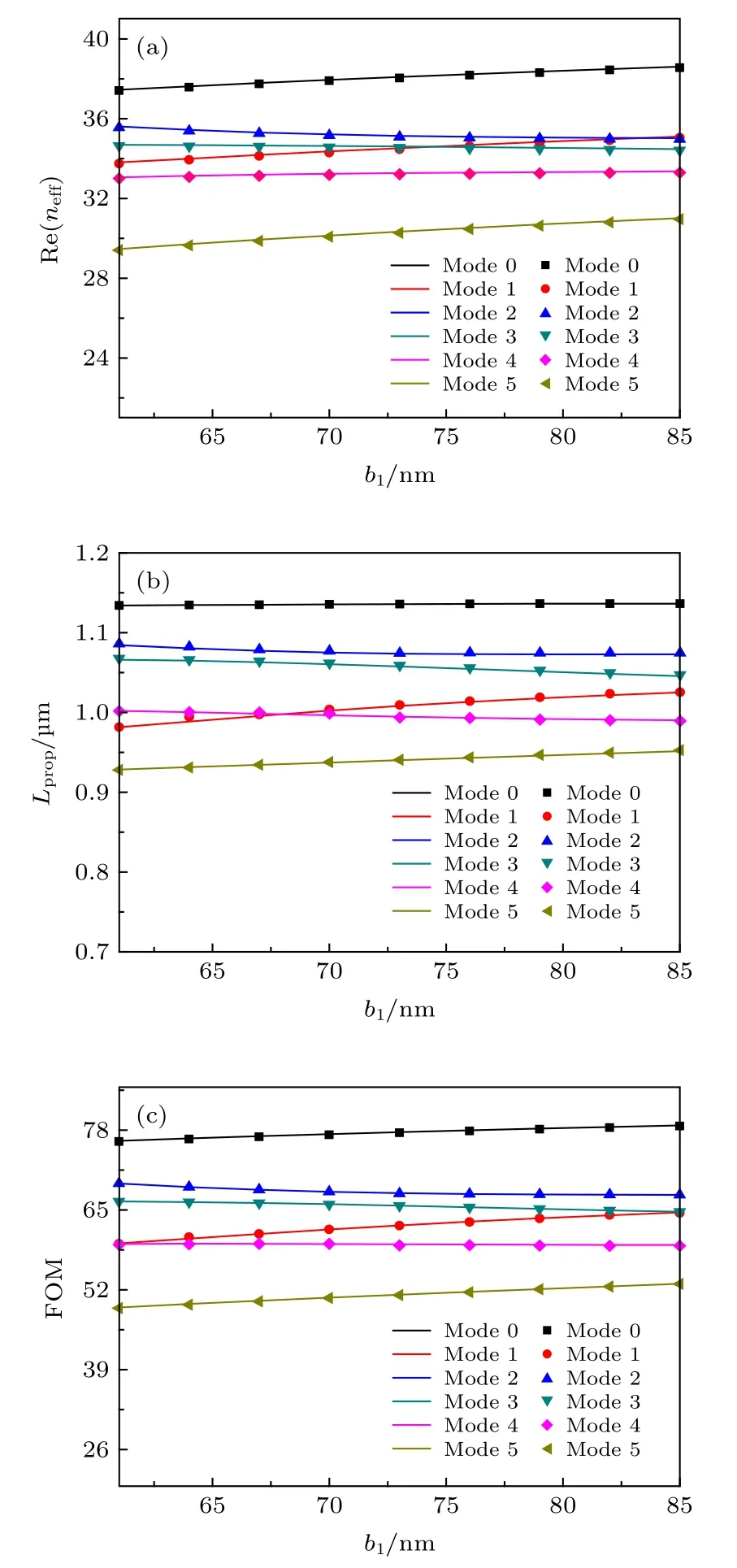
圖7 當 λ=7 μm , E f =0.5 eV , a 1 =90 nm , a 2 =80 nm ,b2 =60 nm , d=35 nm 時, (a)有效折射率實部 Re(neff) 、(b)傳播長度 L prop 和(c)品質因數FOM 隨1 號納米線半短軸b1 變化關系圖Fig. 7. When λ=7 μm , E f =0.5 eV , a 1 =90 nm , a2 =80 nm , b 2 =60 nm,d=35 nm , the dependence of (a) the effective refractive index Re(neff) , (b) the propagation length L prop and (c) the quality factor FOM for the six lowest order modes on the length of b1 on the No.1 nanowire.

需要說明的是, 如果在非弱耦合的條件下,(5)式—(10)式表示的場分布的線性疊加需要修正[44?46]. 本文結果僅在弱耦合的條件下成立.

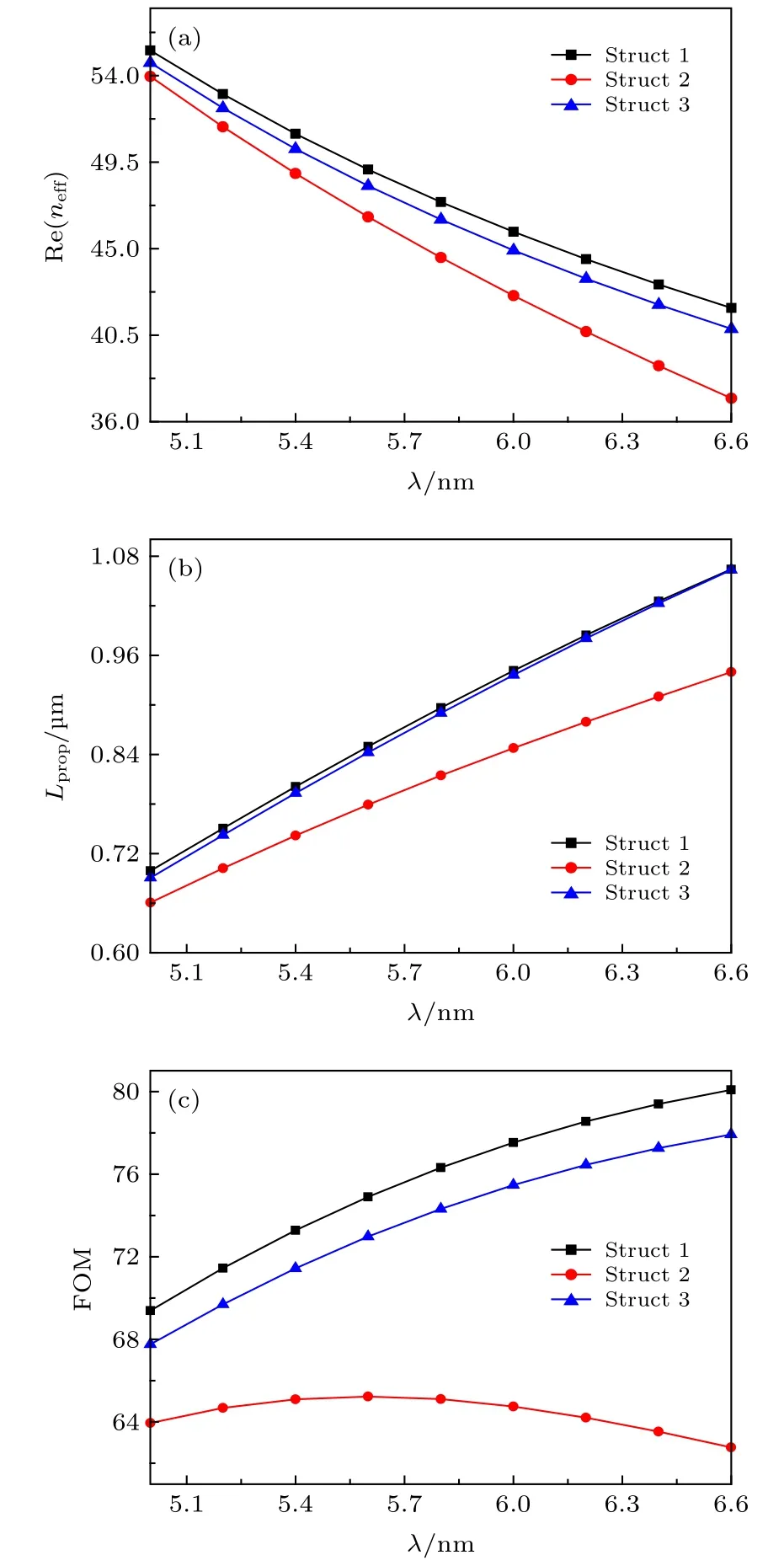
圖8 當 E f =0.5 eV 時, 三種波導結構所支持的基模的(a)有效折射率 Re(neff) 、(b)傳播長度和 L prop 和(c)品質因數FOM 隨波長 λ 變化的關系圖Fig. 8. When E f =0.5 eV , the dependence of (a) the effective refractive index Re(neff) , (b) the propagation length Lprop and (c) the quality factor FOM of the fundamental mode supported by the three structures on the wavelength λ .

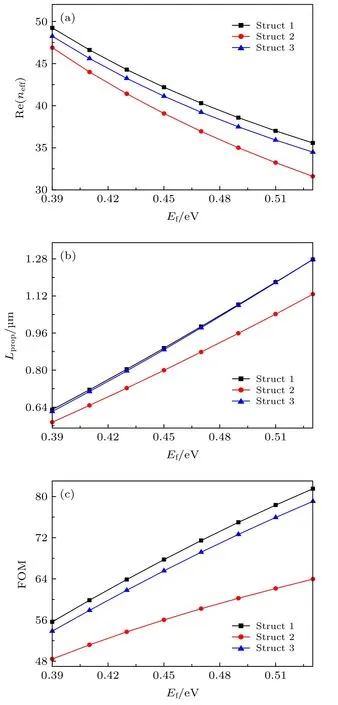
圖9 當 λ=7μm 時,三種波導結構所支持的基模的(a)有效折射率 Re(neff)、(b)傳播長度 L prop 和(c)品質因數FOM 隨石墨烯的費米能級變化的關系圖Fig. 9. When λ=7μm , the dependence of (a) the effective refractive index Re(neff),(b) the propagation length Lprop and (c) the quality factor FOM of the fundamental mode supported by the three structures on the Fermi levels.

4 結 論

本文設計了一種涂覆石墨烯的非對稱橢圓電介質納米并行線光波導, 對其前6 個模式進行了分類, 研究了波導的工作波長、石墨烯的費米能及結構參數與前6 個模式性能之間的依賴關系. 結果表明: 改變波導的工作波長及石墨烯的費米能級, 波導基模的傳輸性能有明顯改善, 增大兩納米線間距時, Mode 0 的傳輸性能下降, Mode 5 的傳輸性能得以改善; 調節1 號納米線的結構參數時, 可對波導傳輸性能進行微調; 同時, 比較了在不同工作波長和費米能下三種結構的波導性能, 結果表明, 在特定條件下, 涂覆石墨烯的非對稱橢圓電介質納米并行線光波導的傳輸性能優于其他兩種結構波導.