橢球膠體在圓球膠體體系中擴散行為的實驗研究*

劉心卓 王華光2)?

1) (蘇州大學, 軟凝聚態物理及交叉研究中心, 蘇州 215006)

2) (蘇州大學材料與化學化工學部, 蘇州 215123)

復雜受限介質中的擴散行為在自然界是普遍存在的, 與其相關的研究涉及物理學、材料科學和生物學等多學科領域, 受到了這些領域研究者們的廣泛關注. 然而, 相比于眾多的圓球受限擴散研究, 對形狀各向異性的粒子在復雜受限介質中的擴散行為的研究依然比較匱乏. 本文提出了一個簡單的軟物質實驗模型—膠體橢球與圓球混合體系, 來研究形狀各向異性的橢球在圓球的受限環境下的擴散行為. 通過描述橢球的運動軌跡和計算粒子的均方位移、范霍夫自關聯函數以及非高斯參量, 發現隨著圓球濃度的增大, 橢球的平動和轉動都被抑制, 出現次擴散行為; 并且, 平動和轉動的位移分布也展現出不同的演化行為, 表明這兩種運動在高濃度下會發生解耦合. 此外, 在不同圓球濃度下, 橢球都趨向于沿自身長軸方向擴散, 因此在沿長軸和短軸方向的平動受到的受限作用的影響也不同, 導致二者也發生解耦合行為. 綜上所述, 受限環境會導致各向異性膠體粒子出現反常擴散行為. 本文的研究有助于理解復雜環境中各向異性物體的擴散和輸運行為.

1 引 言

受限擴散和輸運是普遍存在的物理現象, 如蛋白質在生物體中的輸運[1-3]、示蹤粒子在黏彈性液體中的擴散[4-6]以及藥物在人體器官中的傳遞等[7-9].不同體系中的受限擴散輸運吸引了物理學、材料科學和生物學界越來越多科學研究者的興趣, 研究者們試圖揭示不同受限擴散的物理機制和行為規律[8,10-13]. 由于空間受限, 阻礙了自由的擴散行為,因此受限擴散會出現反常的動力學行為. 例如, 膠體圓球在自由擴散時, 其運動的均方位移(mean square displacement, MSD)與時間呈線性關系,即 M SD～tβ, 擴散指數β= 1. 而當在玻璃體系中時, 由于受到其周圍粒子形成的“牢籠”的限制, 膠體圓球會出現次擴散行為, 此時β< 1[14]. 隨著合成制備技術的發展, 各種形狀各向異性的膠體粒子被制備出來[15,16]. 研究發現膠體粒子的形狀也會對擴散行為產生重要影響[16,17]. 例如, 對于橢球形粒子, 其自由擴散趨向于沿著長軸方向運動, 呈現各向異性的擴散動力學[18]. 更重要的是, 很多的計算機模擬工作表明形狀各向異性的膠體粒子在受限情況下, 其擴散會出現更多有趣和奇異的動力學行為[19,20]. 例如在膠體圓球體系中, 隨著圓球密度的增大, 體系中菱形或四方形的膠體粒子會發生平動擴散和轉動擴散的解耦合(decoupling)行為, 即這兩種運動的演化不一致, 平動動力學比轉動動力學減緩得更快或更慢, 并且解耦合行為與擴散粒子的形狀直接相關[3]. 然而, 相比于眾多的計算模擬研究, 形狀各向異性粒子的受限擴散的實驗研究依然缺乏[21].

本文提出了一個簡單的實驗模型體系來研究形狀各向異性粒子的受限擴散. 將膠體橢球粒子與膠體圓球粒子混合, 研究單個橢球粒子在圓球體系中的擴散行為. 研究發現, 隨著圓球濃度的增大,橢球粒子的平動和轉動都會減弱, 呈現次擴散行為, 而且在高濃度時轉動減緩得更為嚴重, 說明平動和轉動的解耦合行為. 此外, 橢球在不同的圓球濃度下都趨向于沿著自身長軸方向進行平動擴散,說明粒子的平動擴散是由沿著長軸方向的運動主導. 并且, 沿著長軸方向的平動位移會隨著圓球濃度增大出現非高斯分布行為, 而沿著短軸方向的平動位移則沒有變化, 一直接近高斯分布, 說明這兩種平動也發生了解耦合行為. 另外, 轉動位移在中間濃度下出現非高斯行為, 而在更高濃度下非高斯行為又會減弱. 這些結果揭示了圓球受限對橢球擴散行為的重要影響, 有助于更好地認識非球形膠體粒子受限擴散的行為規律.

2 實驗過程與方法

本實驗將少量的橢球與圓球混合, 研究橢球在二維受限體系下的擴散行為. 實驗中使用的圓球是尺寸為1.6 μm 的聚苯乙烯微球, 所用橢球是通過物理拉伸方法制得[3], 長軸約為7.0 μm, 短軸約為1.6 μm. 實驗時使用移液槍吸取適量混合液, 置于兩蓋玻片之間, 從而形成單層膠體粒子樣品, 如圖1所示. 然后利用紫外光膠(norland)對其進行密封.將密封好的樣品靜置10 h 后, 在顯微鏡載物臺上靜置平衡1 h 后進行觀察和數據采集, 采集速度為1 幀/s. 為了防止可能出現的樣品槽邊界效應,選擇遠離邊界的區域來進行數據采集, 并且使視野中只有一個橢球粒子, 避免了橢球粒子之間的相互作用. 圖像數據使用通用的粒子追蹤程序識別和分析. 本文研究了橢球在不同圓球面積分數(φ)下的擴散行為, 其中圓球的面積分數的計算公式為φ=nsπ(σs/2)2/A, 其中ns是圓球的粒子數,σs是圓球粒子的直徑,A表示整個視野的面積.

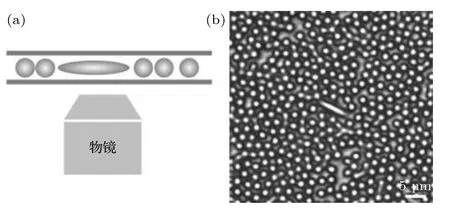
圖1 (a)樣品在顯微鏡物鏡上的示意圖; (b) φ = 0.57 的樣品的顯微鏡照片Fig. 1. (a) Schematic of the experimental sample on a microscope objective; (b) a bright-field microscope image of the colloidal suspension for φ = 0.57.

3 實驗結果與討論

為了直觀展示橢球粒子擴散行為的運動特征,繪制了橢球粒子在不同圓球面積分數下運動100 s的軌跡, 如圖2 所示. 在φ= 0.57 時, 橢球粒子的質心可以在很大的空間內移動, 平動運動明顯, 表現出無規隨機擴散; 粒子取向角度變化頻繁, 其轉動也呈現無規擴散行為. 然而在面積分數較大時(φ= 0.81), 粒子運動的空間范圍減小, 并且粒子的取向幾乎不變, 這表明粒子的擴散在平動自由度和轉動自由度都受到了抑制.

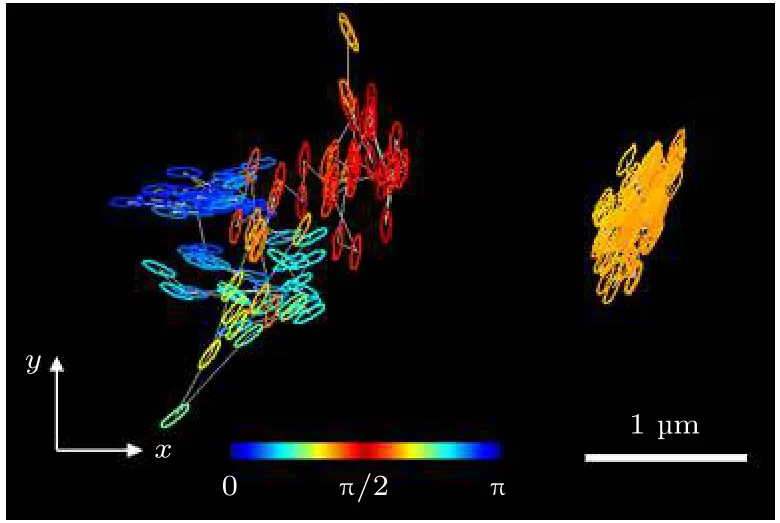
圖2 橢球在不同圓球濃度下運動100 s 的軌跡: φ =0.57(左)和φ = 0.81(右). 橢球的不同時刻位置用空心橢圓表示, 其取向是橢球長軸方向和x 軸方向的夾角, 用顏色表示Fig. 2. 100 s trajectories of an ellipsoid at φ = 0.57 (left panel) and φ = 0.81 (right panel). The positions of the particle at different times are indicated by ellipses. The color indicates the orientation of the particle with respect to the x axis.

為了定量地分析橢球的動力學, 計算了不同圓球面積分數φ下橢球的均方位移(mean square displacement, MSD). 得出橢球平動的MSD 為, 轉動的MSD 為, 其中r(t) 和θ(t) 分別表示t時刻橢球的中心位置和取向. 圖3 展示了橢球在不同圓球面積分數下均方位移. 隨著圓球面積分數φ的增大, 平動和轉動均方位移均減小, 這源于橢球粒子的運動空間受到了周圍圓球粒子的限制, 使其動力學減慢. 并且, 在高圓球面積分數下, 橢球的平動和轉動均方位移都呈現出明顯的次擴散行為. 為了更好反映這種次擴散行為的演化, 對平動和轉動均方位移在1—20 s 的時間范圍內進行冥律(powerlaw)擬合: MSD～tβ, 得到了擴散指數β. 圖4 給出不同圓球面積分數φ下平動和轉動的擴散指數β. 當φ= 0.57 時,β值接近1, 表明圓球粒子的受限影響較小, 橢球表現出普通的擴散行為, 這與軌跡的結果相一致. 隨著φ增大, 平動和轉動的擴散指數都開始減小, 說明橢球因為周圍圓球的受限呈現次擴散行為. 此外, 在較高的圓球面積分數下(φ> 0.75), 轉動的擴散指數比平動的擴散系數下降得更多, 表明橢球的轉動比平動受限嚴重. 說明橢球的轉動擴散和平動擴散在比較強的受限情況下發生了解耦合(decoupling)行為, 這一結果與四面體、菱形等非球形粒子在濃密的膠體體系中的擴散行為一致[16,19], 表明非球形粒子在受限情況下的轉動和平動擴散的解耦合行為具有一定的普遍性.

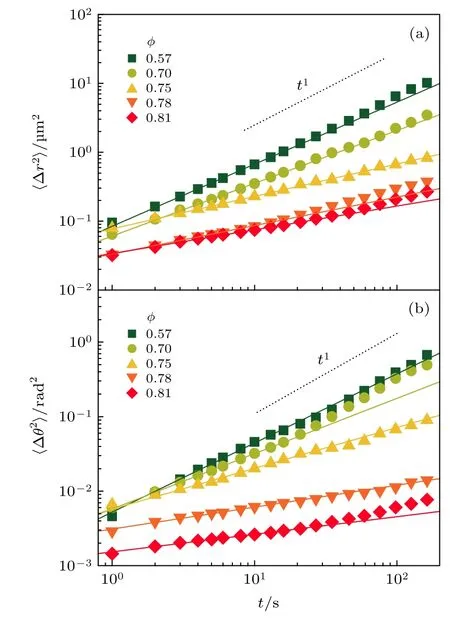
圖3 橢球在不同φ 下的平動均方位移(a)和轉動均方位移(b), 實線是時間范圍為1-20 s 的冪律擬合, ～tβFig. 3. Translational mean square displacements (a) and rotational mean square displacements (b) of ellipsoids at different φ. Solid lines are the power-law fits: ～tβ in the time range of 1-20 s.

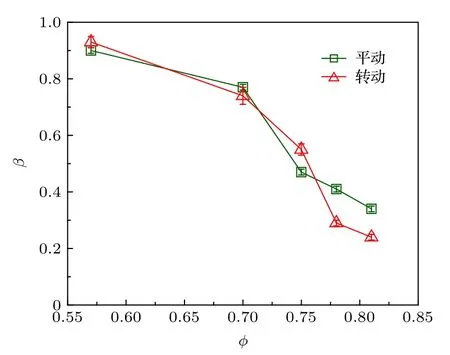
圖4 平動和轉動擴散指數β 隨濃度的變化Fig. 4. The φ dependent β for translational and rotational motions.

為了深入分析橢球粒子的擴散動力學, 本文還計算了范霍夫自關聯函數(self-part of the van Hove correlation function), 用來表征橢球粒子運動位移的概率分布. 對于平動, 范霍夫自關聯函數為Gs(r,t)=〈δ(r-Δr(t))〉; 對于轉動,Gs(θ,t)=〈δ(θ-Δθ(t))〉,其中Δr(t)和Δθ(t)分別是橢球粒子經過t時間運動的平動位移和轉動位移. 對平動進行更細致的分析, 將平動位移分解為兩部分, 即沿著橢球長軸方向的位移和沿著短軸方向的位移. 圖5(a),(b)分別給出了橢球粒子在4 s 內沿著長軸方向和短軸方向的平動位移的概率分布. 結果表明, 在任意圓球面積分數φ下, 沿橢球長軸方向的平動位移分布始終比沿短軸方向的平動位移分布要寬, 說明橢球粒子更傾向于沿其長軸方向進行擴散. 這與在沒有受限情況下的橢球自由擴散行為一致[11], 表明這種各向異性的擴散行為與周圍圓球的受限環境無關.然而, 隨著圓球面積分數φ的增大, 沿橢球長軸方向的平動位移分布逐漸偏離高斯分布, 在高面積分數呈現非高斯行為; 而沿橢球短軸方向的平動位移始終接近高斯分布. 這說明隨著φ的增大, 沿橢球長軸方向和短軸方向的平動行為也發生了解耦合,并非發生同樣的演化行為. 圖5(c)展示了對應的轉動在不同圓球面積分數下的位移分布, 與前面兩種平動位移分布的演化都不相同. 轉動位移分布只在中間面積分數先呈現顯著的非高斯行為. 這進一步說明了隨著φ的增大, 橢球粒子的平動和轉動擴散演化不同步, 兩種運動發生解耦合.

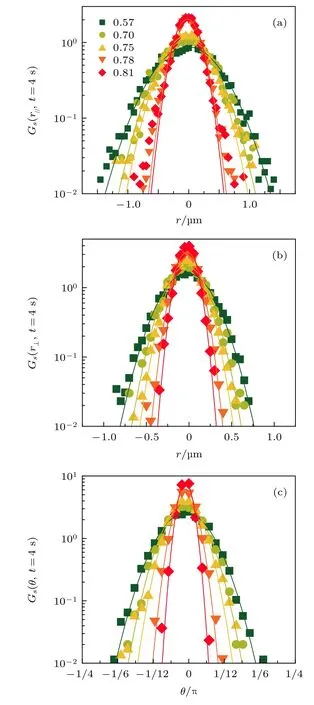
圖5 橢球在不同φ 運動4 s 的位移分布 (a)沿長軸方向平動位移; (b)沿短軸方向平動位移; (c)轉動位移. 實線是高斯擬合Fig. 5. The distribution of the ellipsoid displacement for lag time of 4 s at different φ: (a) Translational displacement along the long axis of the ellipsoid; (b) translational displacement along the short axis, (c) rotational displacement.Solid lines are the best Gaussian fits.

為了進一步確認位移分布的非高斯行為, 計算了非高斯參量:a2= 1/2〈Δ4(t)〉/〈Δ2(t)〉2-1 , 其中Δ(t)代表橢球粒子經過t時間運動的平動位移或轉動位移. 圖6 給出了橢球粒子運動t= 4 s 的平動位移非高斯參量和轉動位移非高斯參量. 對于沿橢球長軸方向的平動位移,a2隨著圓球面積分數φ的增大而變大, 證實了其位移分布越來越偏離高斯行為. 這與膠體玻璃化轉變中的結果相似, 即在體系濃度越來越高時, 粒子運動受到的牢籠效應越來越明顯, 并出現逐漸增強的次擴散行為和非高斯行為[22]. 這里, 隨著圓球面積分數增大, 橢球運動受到由圓球構成的牢籠限制, 從而導致了非高斯行為. 然而, 對于沿橢球短軸方向的平動位移,a2保持很小的值, 表明其接近高斯行為, 與位移分布的結果相一致. 可能的原因是橢球平動趨向于沿長軸方向擴散, 而沿短軸方向的擴散本身就很小,因此牢籠效應主要影響沿長軸方向的運動, 引起非高斯行為; 而對短軸方向的擴散影響較小, 依然保持高斯行為. 對于轉動位移,a2先增大后減小, 呈現非單調變化, 與轉動位移分布結果一致. 這種增大是源于圓球的牢籠效應, 而減小則可能由于在很大的圓球面積分數下, 相比于平動, 橢球的轉動已經被強烈限制[22], 均方位移的結果也說明了這一點. 因而導致了a2減小, 使轉動位移趨向高斯位移分布. 這與圓球膠體體系發生玻璃化轉變后的非高斯行為相似, 這種情況下粒子平動運動被凍結后,非高斯行為會減弱[11]. 在本文的體系中, 由于橢球在高面積分數下, 其轉動相比于平動先被凍結[22],因而轉動的非高斯行為會在高面積分數下減弱, 對應的位移分布又趨向高斯行為.

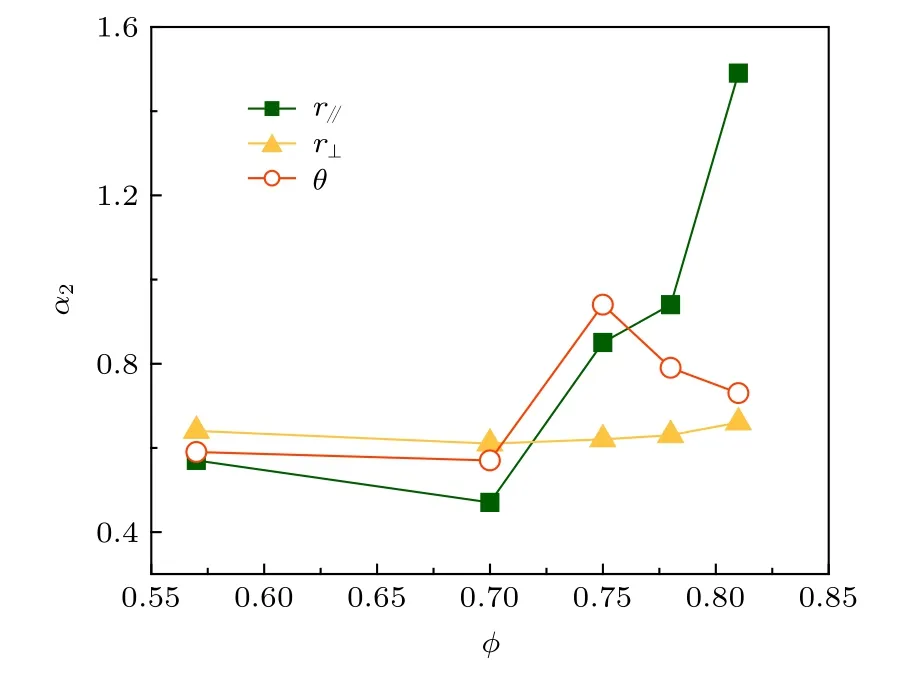
圖6 橢球運動4 s 沿長軸平動位移 (r//), 沿短軸平動位移 (r⊥) 和轉動位移 (θ) 的非高斯參量Fig. 6. The non-Gauss parameter of the displacement of ellipsoid for lag time of 4 s: Translational displacement along the long axis of the ellipsoid (r//), translational displacement along the short axis (r⊥), and rotational displacement (θ).

4 總 結

利用攝像顯微技術研究了橢球粒子在膠體圓球體系中的擴散行為. 通過對橢球粒子動力學行為的分析, 包括運動軌跡、均方位移、范霍夫自關聯函數以及非高斯參量, 揭示了其在不同圓球濃度受限條件下的擴散行為演化. 結果表明, 隨著圓球濃度的增大, 橢球粒子的平動和轉動都變慢, 并且平動和轉動在高濃度下變化不一致, 發生解耦合行為. 對于不同圓球濃度, 橢球表現出各向異性的擴散行為, 即趨向于沿橢球長軸方向擴散. 因此隨著圓球濃度的增大, 沿長軸方向的平動會受到很強的受限, 其位移出現非高斯行為并逐漸增強; 而沿短軸方向的平動受到的影響較小, 其位移分布一直接近高斯行為. 這說明這兩種平動行為隨著圓球濃度的增大也發生了解耦合. 此外, 橢球轉動位移的非高斯行為在高濃度會減弱, 與兩種平動擴散都不一樣, 進一步說明了橢球粒子在受限條件下平動和轉動發生解耦合. 本文研究揭示了圓球受限對橢球粒子擴散動力學行為的重要影響, 有助于深入理解復雜微環境中各向異性粒子的運輸和傳遞.