超聲速橫向氣流中液體射流的軌跡預測與連續液柱模型*

周曜智 李春 李晨陽 李清廉?

1) (國防科技大學空天科學學院, 長沙 410073)

2) (國防科技大學, 高超聲速沖壓發動機技術重點實驗室, 長沙 410073)

對于液體射流沿壁面法向噴注進入超聲速橫向氣流中的射流軌跡開展了理論與實驗研究, 建立了連續液柱三維實體模型. 基于液體微元受力分析建立了連續液柱沿噴注方向橫截面的截面變形控制方程, 計算了液體射流軌跡與橫截面變形, 合理考慮了液體射流因發生表面破碎所引起的質量損失, 提出適用于超聲速橫向氣流的連續液柱模型. 利用高時空分辨率的顯微成像方法拍攝超聲速橫向氣流中連續液柱的瞬時圖像, 研究的參數變量包括液體噴注壓降(1—2 MPa)、液體噴嘴直徑(0.5 mm/1.0 mm)及液氣動量比(3.32—7.27).研究結果表明, 采用連續液柱模型可以較好地預測中心面上的射流軌跡和三維空間上的液柱形態, 并可較為真實地反映實際流場特征, 預測結果與實驗結果吻合良好.

1 引 言

在超燃沖壓發動機的燃燒室中, 液體燃料經壁面法向噴注進入超聲速的橫流氣體中, 在強烈的氣動力作用下, 液體射流發生變形并向下游方向逐漸彎曲, 此間伴隨發生一系列的霧化與混合過程. 在近液體噴嘴出口區域, 射流可以保持較為光滑的連續液柱形態, 但由于Rayleigh-Taylor 不穩定性[1]引起的表面波對射流迎風面的持續作用, 射流柱最終發生斷裂, 此為液體射流的液柱破碎. 與此同時,大量細小的液滴由于強剪切力的作用從液柱兩側直接剝離[2], 在射流柱周圍形成密集的液滴群, 此為液體射流的剪切破碎. 通過液柱破碎和剪切破碎, 大尺度的連續液柱結構破碎形成小尺度的液塊和液滴.

射流軌跡和穿透深度是描述射流空間狀態的兩個概念. 前者通常是指自液體噴嘴出口處至液柱破碎位置的射流噴注路徑, 而后者一般是指射流在不同流向位置穿透到橫向氣流中的最大穿透程度,也可理解為噴霧羽流的上邊界[3], 在本文所關注的近液體噴嘴出口區域, 射流軌跡與穿透深度含義相同, 射流軌跡可認為是穿透深度的初始段. 由于穿透深度可以較好地表征出射流/噴霧在噴注方向上的空間分布特征[4], 研究者采用光學觀測手段對超聲速橫向氣流中液體射流穿透深度進行了實驗研究并經過射流邊界擬合得到了大量的經驗公式[5?7],這些經驗公式的表達形式一般分為冪函數、指數函數和對數函數三種形式. 實驗結果表明, 液氣動量比(q)、噴嘴下游沿流向的無量綱距離(x/d)、噴注角度(θ)和韋伯數(We)是影響液體射流穿透深度的主要因素[5,8?14]. 由于研究者們采用的光學成像原理、實驗拍攝條件和圖像處理手段不盡相同,這導致基于實驗結果擬合得到的經驗公式普適性較差, 無法將結論進行有效的推廣. 吳里銀等[15]采用脈沖激光背景光方法研究了多種工況條件下射流的瞬態邊界振蕩分布規律, 引入邊界帶的概念代替穿透深度并建立了射流振蕩分布的經驗模型, 成功預測了水射流在Ma= 2.1 橫流中的振蕩分布及穿透深度, 進一步提高了穿透深度經驗公式的普適性.

在超聲速橫向氣流中, 液柱斷裂破碎的過程與亞聲速橫流中液柱斷裂破碎的過程極為相似, 其在近噴嘴區域也存在特征較為明顯的連續液柱結構[16].Mashayek 等[17]采用理論分析的方法對于亞聲速橫流中液體射流軌跡進行了研究, 綜合考慮了因剪切破碎引起的液體微元質量損失與液柱橫截面隨時間的形變規律, 計算得到的射流軌跡與實驗結果吻合較好. 李春[18]采用高速激光陰影方法研究了近噴嘴區域射流的精細結構與表面波特征, 闡明了表面波控制射流液柱破碎的機理, 提出了射流表面波振幅與波長的空間演化規律. 周曜智等[16]基于流體體積函數(volume of fluid, VOF)兩相流模型并結合自適應網格在Fluent 軟件中數值計算了水射流在Ma= 2.85 橫流中的破碎過程, 研究了多種工況條件下連續液柱空間結構的變化規律. 研究表明: 自適應網格可以大幅縮減計算網格量并進一步提高兩相流計算效率, 計算得到的射流軌跡與實驗結果吻合較好. VOF 模型和CLSVOF(couple level set and volume of fluid)模型對于射流一次霧化過程的仿真存在較大優勢[19?22], 但其計算結果極為依賴氣液界面位置的網格分辨率, 而液體射流破碎過程是典型的跨尺度兩相流問題(1 μm—1 mm), 噴霧下游的小尺度液滴往往由于網格分辨率不足被忽略計算. 為有效計算出下游小尺度液滴并對其霧化特性進行分析, Ashgriz 等[17]與Douglas等[23]采用實體-粒子耦合建模的方式, 將亞聲速橫流條件下一次破碎的連續液柱結構認為是物理實體, 并在連續液柱表面增添二次破碎初始液滴與二次破碎模型, 實現了噴霧全場的低成本計算, 其計算得到的下游液滴速度和液滴直徑與實驗結果吻合較好. 采用實體-粒子耦合建模的方式研究液體射流霧化破碎過程有三個明顯的優點: 其一, 基于理論分析建立的連續液柱實體結構使得氣流場的特征更為合理, 可定量預測液體射流軌跡; 其二,將連續液柱簡化為物理實體, 有效地降低了用于捕捉射流一次破碎的計算網格量; 其三, 依照實驗結果添加二次破碎初始液滴, 從而完成噴霧全場的精確數值計算, 實現下游液滴霧化特性的定量預測.由于實體-粒子耦合建模在預測亞聲速橫流中射流軌跡和下游液滴霧化特性等方面存在巨大優勢, 因此, 本文嘗試將其在超聲速橫流條件下進行合理推廣, 以期達到預測超聲速橫流條件下液體射流軌跡、射流柱三維空間形態和下游液滴霧化特性的目的. 超聲速橫流下的液體射流一次破碎過程與亞聲速橫流下的液體射流一次破碎過程具有較多相似點. 其一, 由于壁面邊界層的存在, 兩者在近噴嘴區域都存在相似的連續液柱結構; 其二, 受氣動加速影響, 兩者在液柱迎風面均存在相似的表面波結構; 其三, 因氣動剪切影響, 兩者在液柱兩側均會發生剪切破碎. 與此同時, 兩種橫流條件下射流的一次破碎過程也存在一定差異. 超聲速橫流由于其具有更高的湍動能, 因此液體射流破碎過程往往也更加復雜. 比如, 由于液體射流對超聲速橫流的阻礙作用, 射流前方會形成一道特有的弓形激波, 這使得液柱迎風面上不同高度位置的氣流速度存在較大差異, 而在亞聲速橫流中, 這一速度被認為是均勻一致的. 由于經過弓形激波后的橫流速度仍然顯著高于亞聲速橫流速度, 因此, 超聲速橫流下的射流柱變形、斷裂和破碎過程發生更快, 液柱破碎位置更靠近噴嘴出口, 液柱破碎時間更短.

本文首先基于微元分析的方法研究了超聲速橫流條件下液體微元的受力情況, 建立了連續液柱沿噴注方向橫截面形變方程, 考慮弓形激波的影響對橫流氣動力進行了合理修正, 提出了可同時預測液體射流軌跡與射流柱三維空間形態的CLC 連續液柱模型(continuous liquid column model). 最后基于PIV(particle image velocimetry)系統與顯微鏡頭提出了一種高時空分辨率的顯微成像方法, 拍攝得到了近噴嘴區域精細的連續液柱結構并對于CLC 模型計算結果進行了實驗驗證.

2 實驗系統與數值仿真方法

2.1 超聲速風洞與試驗件

本文實驗是在國防科技大學高超聲速沖壓發動機技術重點實驗室二維下吹式超聲速風洞[15]中進行的, 超聲速噴管出口橫截面為50 mm × 60 mm(H×W), 試驗段長度為200 mm, 超聲速風洞系統示意圖如圖1 所示. 風洞采用直連式設計, 工作過程如下: 上游高壓空氣在進入駐室段、穩定段后,紊流度大幅降低, 進入Laval 噴管后加速至設計馬赫數進入試驗段, 試驗段出口與環境大氣直接相連. 風洞采用高壓儲氣罐提供高壓的空氣作為氣源, 儲氣罐體積為20 m3, 空氣氣源壓力大于10 MPa.風洞系統可通過調節駐室總壓, 靈活調節試驗段內超聲速氣流的靜壓、密度等流動參數. 論文研究中分別應用了馬赫數Ma= 2.1 和Ma= 2.85的兩種噴管, 兩種馬赫數下對應的氣流參數如表1所列.

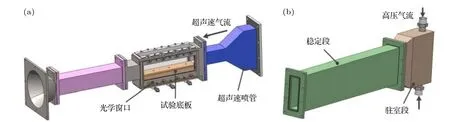
圖1 超聲速風洞系統示意圖[18]Fig. 1. Schematic diagram of supersonic wind tunnel system[18].

表1 超聲速橫流參數Table 1. Supersonic cross flow parameters.

2.2 顯微成像系統

為了驗證CLC 模型預測射流軌跡的準確性,利用超聲速風洞、雙脈沖固體激光器、QM1 長距離工作鏡頭和CCD 相機搭建了超聲速液體射流顯微成像系統, 主要對比采用實驗和理論計算兩種方式得到的射流軌跡的差異, 成像系統原理圖如圖2 所示. 脈沖激光經過激光擴束器后, 通過散射板形成均勻分布的平面背景光源. 同時采用PIV 系統控制軟件完成計算機、CCD 相機和同步控制器的同步控制; 激光器最大能量為500 mJ, 波長為532 nm,單脈沖寬度為7 ns, 能夠提供足夠的時間分辨率,保證“凍結”射流瞬態結構, 而不出現“拖影”現象[15],從而獲得清晰的近場射流圖像. 實驗采用的CCD相機成像單元分辨率為 4000 × 2672.

圖2 顯微成像系統原理圖Fig. 2. Schematic diagram of microscopic imaging system.

圖3(a)為實驗中所使用的QM1 鏡頭, 其工作距離為0.55—1.52 m, 可實現對毫米級圓形視場的成像觀測, 圖3(b)為QM1 鏡頭工作特性曲線,QM1 鏡頭工作距離越小成像視場越小, 相應圖像的空間分辨率則越高. 實驗中 QM1 鏡頭的工作距離取為0.6 m, 顯微成像實驗獲得的原始圖像空間分辨率為1.57 μm/pixel.

2.3 氣動阻力系數計算

采用數值仿真的方法計算連續液柱橫截面的氣動阻力系數, 計算中將連續液柱橫截面氣動阻力系數的計算簡化為同等條件下二維液滴氣動阻力系數的計算. 圖4 為氣動阻力系數計算域, 二維圓形液滴直徑為1.0 mm. 由于液滴繞流流場存在對稱性, 因此選取沿液滴水平中心線一半的流場區域作為計算域, 其中邊界1 為橫流入口, 設定壓力入口邊界條件, 總壓為1.41 MPa; 邊界2, 5 分別為壁面與液滴表面, 給定無滑移壁面邊界條件; 邊界3為橫流出口, 設定壓力出口邊界條件; 邊界4 為對稱面, 給定對稱邊界條件. 采用基于密度基的求解器進行計算, 湍流模型選擇k-ωSST 模型, 控制方程采用二階迎風格式求解. 采用三種不同分辨率的網 格 對Ma= 2.85,總 壓 為1.41 MPa,總 溫 為300 K 橫向氣流中直徑為1.0 mm 的圓形二維液滴的流場進行數值計算, 對液滴附近的網格進行了局部加密(圖5). 表2 為采用三種網格計算得到氣動阻力系數. 由表2 中數據可知, 中等網格和密網格計算得到的阻力系數基本相同. 圖6 與圖7 分別給出了對稱面上流向速度分布及二維液滴表面的壓力分布, 中等網格與密網格的分布曲線基本吻合. 綜合考慮數值計算的精度需求和計算效率, 選擇中等網格進行液滴阻力系數的計算. 針對不同橢圓率e(e=b/a)的二維液滴進行計算時, 保持網格數量與中等網格數量相同, 液滴表面的最小網格尺寸為 0.01d.

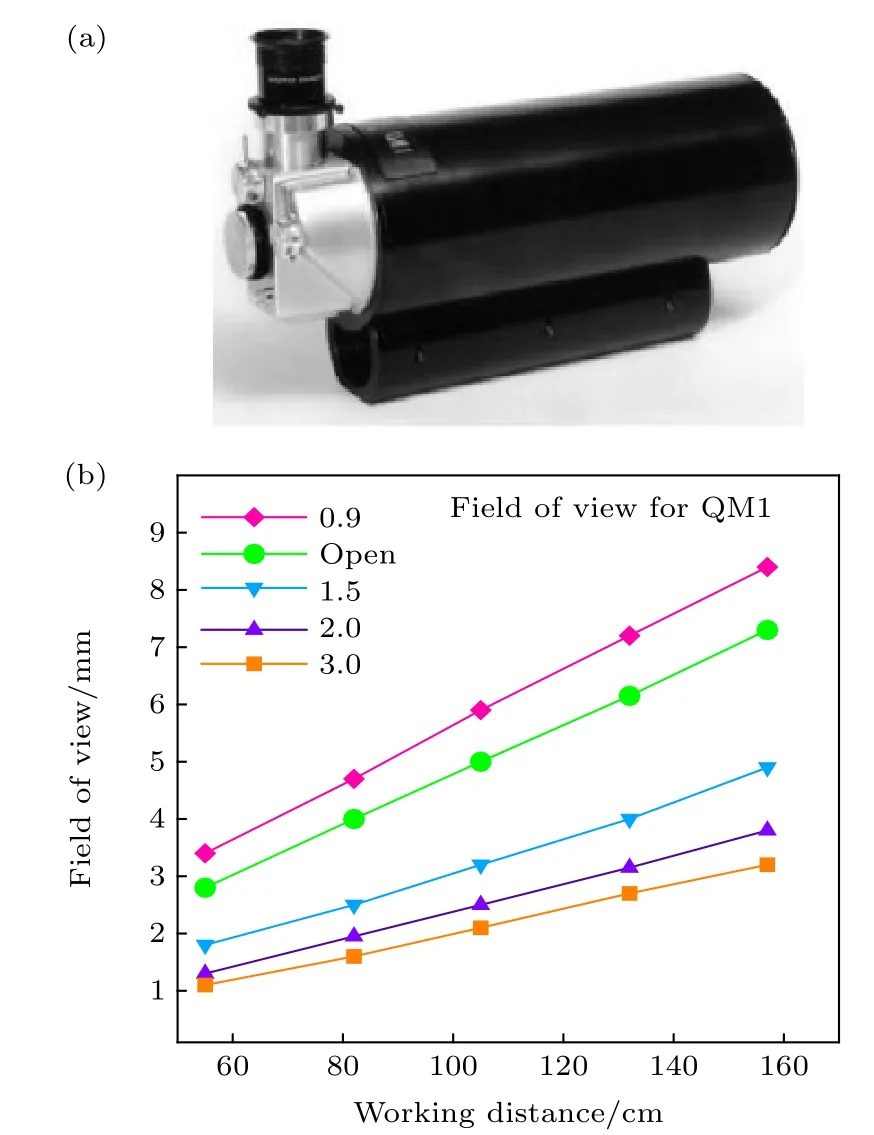
圖3 顯微成像系統原理圖 (a) QM1 鏡頭; (b) QM1 鏡頭工作特性曲線Fig. 3. Schematic diagram of microscopic imaging system :(a) QM1 camera lens ; (b) QM1 microscopy camera lens working characteristic curve.

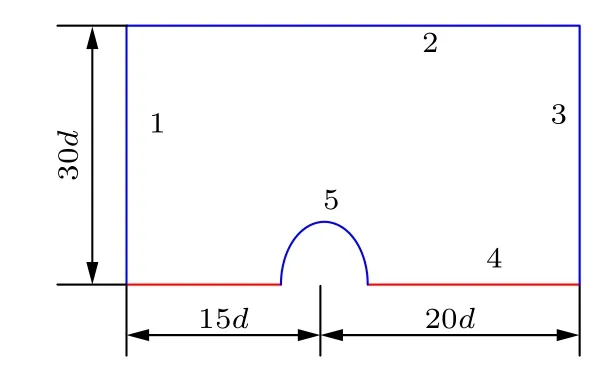
圖4 液體微元的受力分析示意圖Fig. 4. Aerodynamic drag coefficient calculation domain.

圖5 二維液滴附近網格Fig. 5. Grids near the 2D droplet.

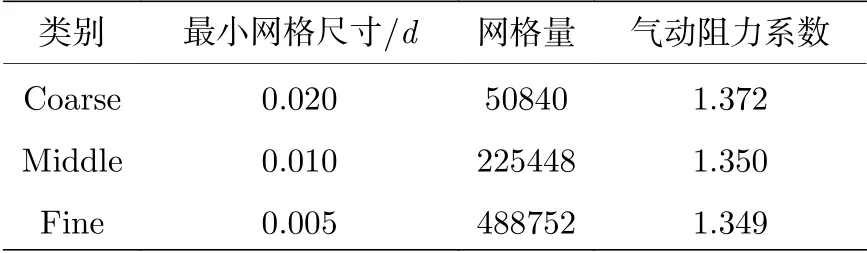
表2 不同網格計算得到的氣動阻力系數Table 2. Aerodynamic drag coefficients calculated from different grids.

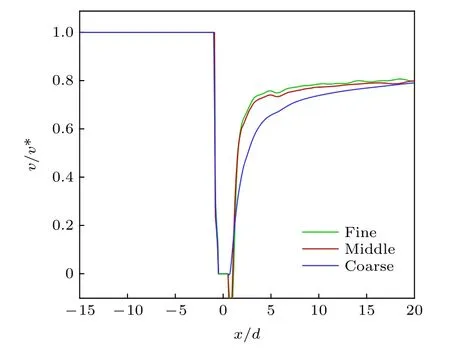
圖6 對稱面流向速度分布Fig. 6. Symmetrical flow velocity distributions.

圖7 二維液滴表面靜壓分布Fig. 7. Surface static pressure distributions of 2D droplet.

3 連續液柱建模

圖8 為超聲速橫向氣流中連續液柱變形分區示意圖, 主要分為光滑液柱區域、彎曲液柱區域與稠密液塊區域. 本文研究的連續液柱是指液體噴嘴出口到液柱斷裂之間的連續液體部分, 它包含了光滑液柱區域與彎曲液柱區域. 在超聲速橫流的持續作用下, 液體射流柱迎風面出現表面波并伴隨出現液滴剝離的現象, 表面波不斷發展使得射流柱斷裂并形成大尺度的液塊, 這一過程為液體射流一次破碎過程. 其中, 射流柱斷裂過程是一次破碎過程中最為重要的特征. 由于亞聲速橫流情況下表面波的發展較慢, 射流柱表面一般較為光滑. 由于壁面邊界層的存在, 近噴嘴區域氣流速度較低, 液體射流依然存在特征明顯的連續液柱結構, 但由于橫流氣動力較強, 射流柱同時在多個方向上發生劇烈的結構變形, 并伴隨部分液滴從射流柱兩側直接剝離的現象, 這使得射流柱附近的氣相流場變得極為混亂, 研究難度較大.

圖8 連續液柱變形分區示意圖Fig. 8. Schematic diagram of continuous liquid column deformation partition.

為研究射流柱附近復雜的氣相流場, Li 等[24]對實驗結果和數值計算結果進行了時間平均處理,并從中總結了氣相流場中存在的普遍規律, 由此發現并證實了射流下游反轉漩渦對的存在. 本文同樣采用基于時間平均的方法, 提出直接建立具有表征時均特征的連續液柱(實體), 從而實現實體-粒子耦合建模. 若要實現超聲速橫流條件下實體-粒子耦合的建模, 首先需要完成一次破碎“實體”的建立, 再通過“粒子”實現下游液滴霧化特性的預測.本文提出建立一種可較好表征氣相流場時均特征的連續液柱實體模型, 該模型可用于計算一次破碎的“實體”, 模型建立前提出以下四點假設(如圖9所示):

1) 忽略連續液柱表面的非定常特征, 著重考慮連續液柱的定常特征, 液柱表面光滑, 射流軌跡為光滑曲線;

2) 簡化實際情況下射流柱在橫向氣流作用下的非軸對稱空間變形過程, 認為射流橫截面發生軸對稱變形且橫截面形狀由圓連續的變為橢圓;

3) 射流橫截面氣動阻力系數的計算簡化為二維橢圓液滴氣動阻力系數的計算;

4) 將液柱前方的弓形激波簡化為一道激波角已知的斜激波, 波后馬赫數按照斜激波波后馬赫數進行計算, 從而獲取液柱迎風面上不同高度位置的氣流速度.

連續液柱的空間結構可以近似認為是一段不斷發生變形的三維“水管”, 連續液柱在中心截面的投影可以認為是這段“水管”的二維投影, 其迎風面的“管壁”表示的是中心截面上的射流上邊界, 即射流軌跡; 其背風面的“管壁”表示的是中心截面上的射流下邊界. 此外, 射流柱在噴注方向的投影可以近似認為是二維橢圓[25], 自液體流出噴嘴至射流一次破碎結束, 該方向上的投影形狀由與噴嘴出口直徑等大的圓形連續變形為橢圓形. 其中, 橢圓長軸為2a, 短軸為2b, 橢圓率為e(e=b/a). 隨著液體的流出, 橢圓的長軸不斷變長, 短軸不斷變短(如圖10 所示).

圖9 模型假設示意圖(粉色為液體射流一次破碎大渦模擬結果[19?22])Fig. 9. Schematic diagram of model hypothesis (The pink region is the result of large eddy simulation of liquid jet primary breakup[19?22]).

圖10 液體微元橫截面變形示意圖Fig. 10. Schematic diagram of cross-section deformation of liquid microelements.

3.1 液體微元受力分析

液體射流噴入超聲速橫流后, 受氣動力、表面張力和黏性力的共同作用發生霧化破碎. 為清晰地描述液體射流柱的受力情況, 提取液體射流柱中一段微元薄片進行受力分析, 其中微元薄片厚度為h.類比二維受力彈簧系統[26], 對受外界壓力作用的二維液滴變形過程進行了受力分析, 二維液滴的變形主要受黏性力Fv、表面張力Fs和外界壓力Fp的聯合作用, 通過計算這三種力的線性項, 最終在x2方向上建立了力平衡方程:

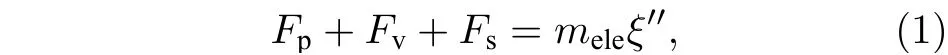
式中,mele為半液滴微元質量(0.5ρjπabh) ;ξ為半液滴微元質心到液滴微元中心的距離,ξ的初值為4r0/(3π) (圓形), 變形過程中為 4a/(3π) (橢圓形).

采用半液滴微元的質心運動來間接表示液體微元的運動, 并通過將每單位厚度液滴微元的能量耗散除以2ξ以獲取黏性力, 黏性力的表達式為[17]

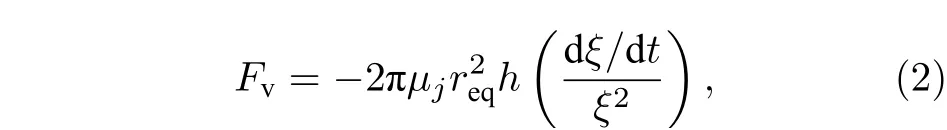
式中,μj為液體黏性;req為與瞬時橢圓橫截面面積相等的等效圓的圓直徑;req的值為(a+b)0.5, 由于橢圓橫截面長軸長度與短軸長度的變化遠大于req, 故認為req是常數.

半液滴微元表面張力的表達式[17]為

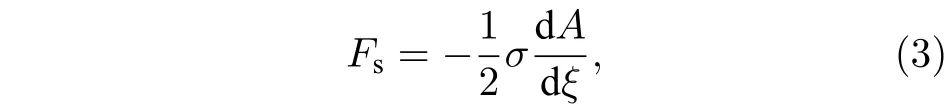
式中,σ為液體表面張力系數;A為液體微元側面的表面積; 液體微元側面的表面積為

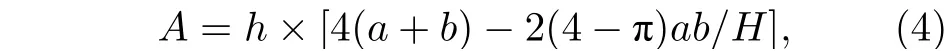
式中,H的表達式為

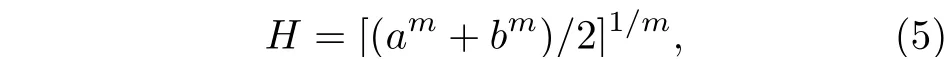
m的值取0.825, 將(4)式和(5)式代入(3)式, 得到半液體微元的表面張力的表達式[17]為

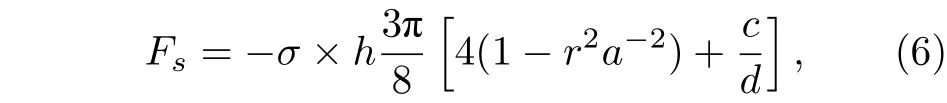
c和d均為常數:

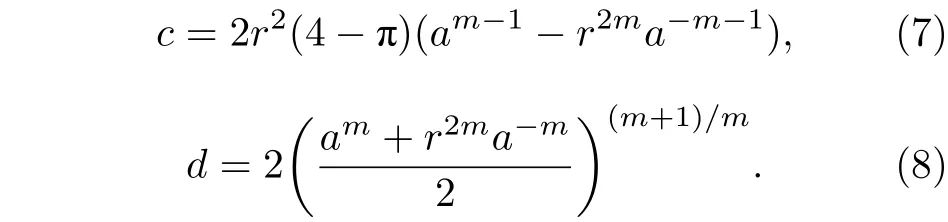
外部壓力做的功[17]為

式中,Ap為壓力作用面積(Ap=b×h);p為橫流氣體的總壓

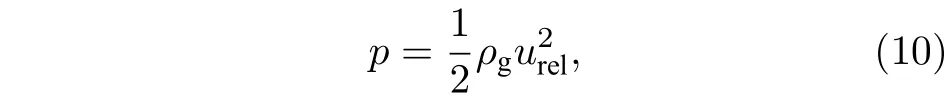
urel為橫流氣體相對于液體微元的相對速度,

式中ug為射流柱前方實際橫流速度, 下文對此速度進行了修正;θ為偏轉角, 表示橫流方向與液體微元的夾角.

將(10)式和(11)式代入(9)式, 外界壓力的表達式為

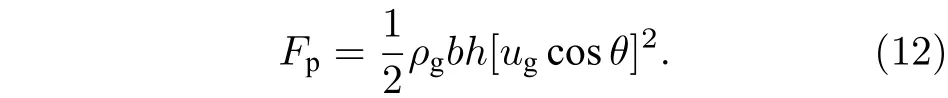
將(2)式、(6)式和(12)式代入(1)式后, 得到了液體射流柱橫截面形變方程:

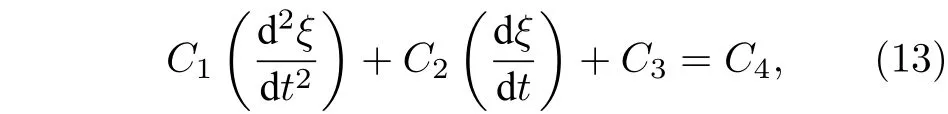
C1,C2,C3和C4的表達式為

由牛頓第二定律, 液體微元受氣動力和剪切力的聯合作用(圖11), 其中Faero為氣動力,F1為液體微元與下方微元間的剪切力,F2為液體微元與上方微元間的剪切力.

液體微元所受氣動力Faero為

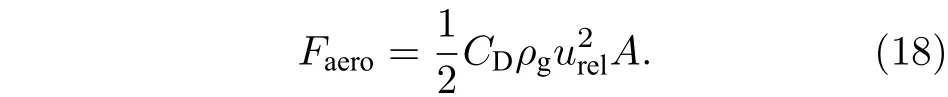
式中,A=2a×h, 將(11)式代入(18)式, 得

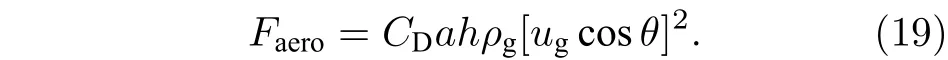
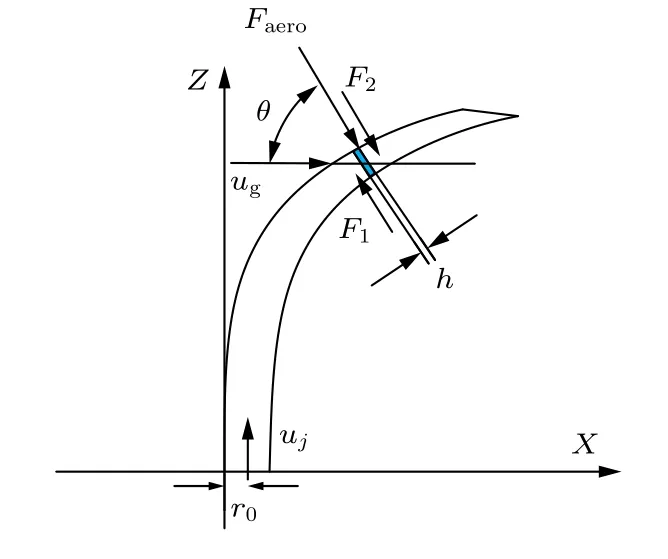
圖11 液體微元的受力分析示意圖Fig. 11. Schematic diagram of force analysis of liquid microelements.

Inamura[27]與Mashayek 等[17]對于液體微元的運動過程進行了分析, 液體射流沿射流軌跡方向速度保持恒定不變并且始終等于初始液體射流速度, 因此, 液體微元在x與y方向上的運動學方程:

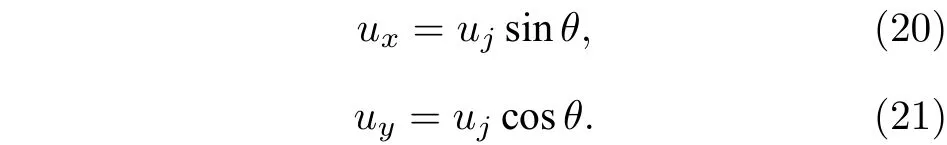
對于完整的液體微元, 由牛頓第二定律可知:

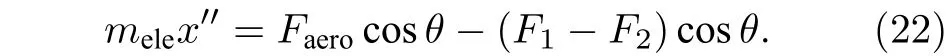
將(20)式對時間進行微分后代入(22)式后,獲得了求解θ的一階微分方程,

式中,Fshear表示的是上下相鄰液體微元作用于所分析微元的剪切力合力, 其表達式如下:

式中,κ射流軌跡的當地曲率為

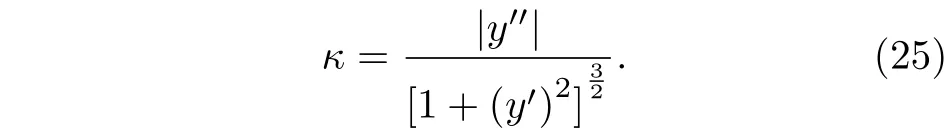
將(21)式對時間進行微分后代入(25)式, 當地曲率的表達式變為

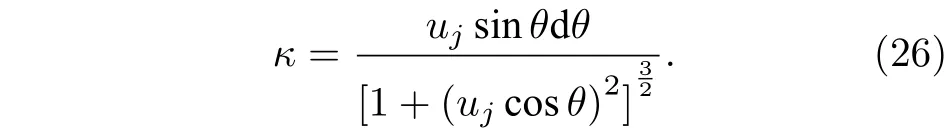
文中的射流軌跡是通過計算微元質心運動軌跡后間接獲得的, 射流軌跡與微元質心運動軌跡的關系為

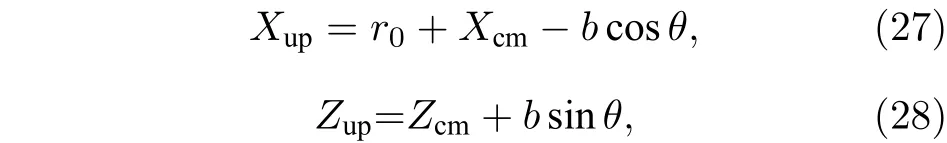
式中,Xcm,Zcm為液體微元質心運動軌跡對應的x方向坐標與z方向坐標.

3.2 液體微元氣動力計算與修正

由3.1 節液體微元受力分析可知, 氣動阻力系數CD和射流柱前方實際橫流速度ug是影響液體射流柱橫截面變形的兩個重要因素. 對于氣動阻力系數的計算一般分為兩種: 一種是對于固定的破碎模式, 氣動阻力系數也是一個定值[27?29], 計算時取一個經驗常數即可; 另一種是忽略液體射流的三維效應, 將射流柱簡化為二維液滴, 在CFD軟件中計算不同橢圓率液滴的氣動阻力系數, 之后通過線性插值的方式估計射流柱的氣動阻力系數.Mashayek 等[17]采用這一方法計算了二維液滴的氣動阻力系數, 并以此估計了射流柱的氣動阻力系數.

圖12 為無量綱速度云圖, 超聲速氣流受液滴阻礙在液滴前形成弓形激波, 激波的脫體距離為0.425 mm, 這一距離與吳里銀[30]實驗得到1 mm射流弓形激波的脫體距離相近, 故本文采用的二維簡化方法在一定程度上能夠反映射流受到的氣動阻力. 通過計算液滴附近的壓力, 可得到多個橢圓率下液滴的氣動阻力系數, 從而獲得氣動阻力系數隨橢圓率的變化關系(圖13).

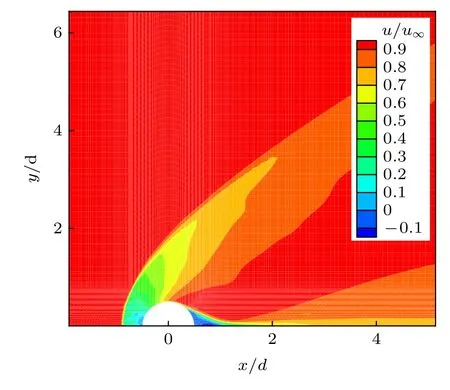
圖12 二維液滴附近流向速度分布Fig. 12. Flow velocity distribution of 2D droplets.

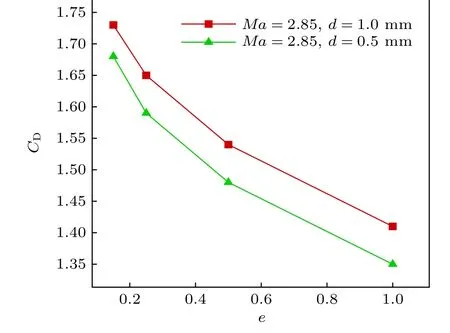
圖13 二維液滴氣動阻力系數CDFig. 13. Aerodynamic drag coefficient of 2D droplet CD.

橫向氣流經過弓形激波后, 速度、方向均發生改變, 如果直接采用噴管出口的速度作為液柱前方的橫流速度, 那么計算結果就會出現較大的偏差.圖14(a)為李春[18]采用激光紋影拍攝得到的液體射流一次破碎結果. 從圖14(a)中可以發現, 在超聲速橫流條件下, 液體射流前方存在一道明顯的弓形激波. 橫向氣流經弓形激波后, 方向發生改變,速度明顯降低. 如圖14(c)所示, 本文將這道弓形激波簡化為一道激波角已知的斜激波, 通過計算斜激波后的橫流速度等效替代實際弓形激波后方的橫流速度, 并基于此對氣動力進行了修正. 如圖15所示, 將斜激波前后的速度沿垂直與平行激波方向進行分解, 其中腳注“n”表示速度的垂直分量, 腳注“t”表示速度的平行分量.

橫流轉折角δ的計算公式為

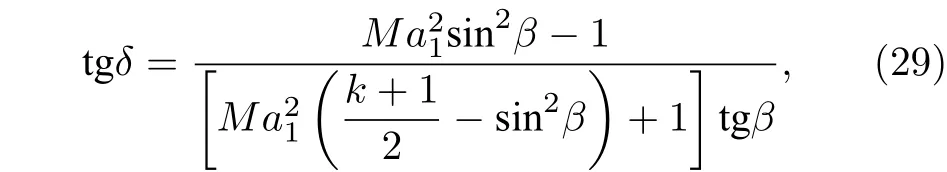
式中,Ma1表示斜激波前橫流馬赫數;β為激波角.

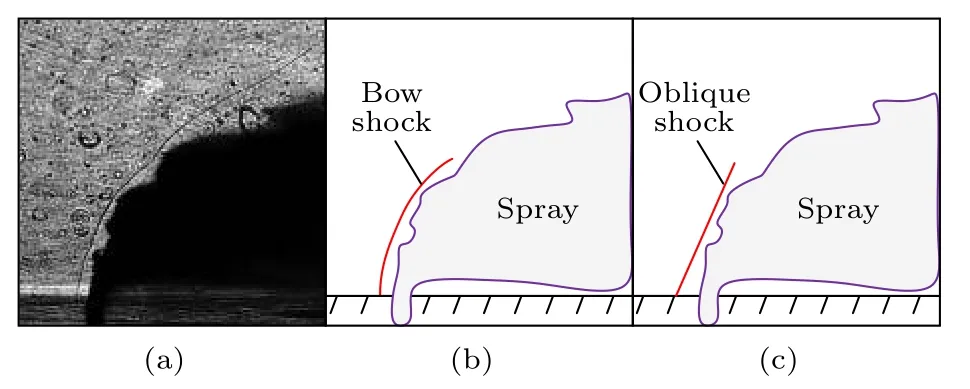
圖14 斜激波簡化示意圖Fig. 14. Simplified schematic diagram of oblique shock.

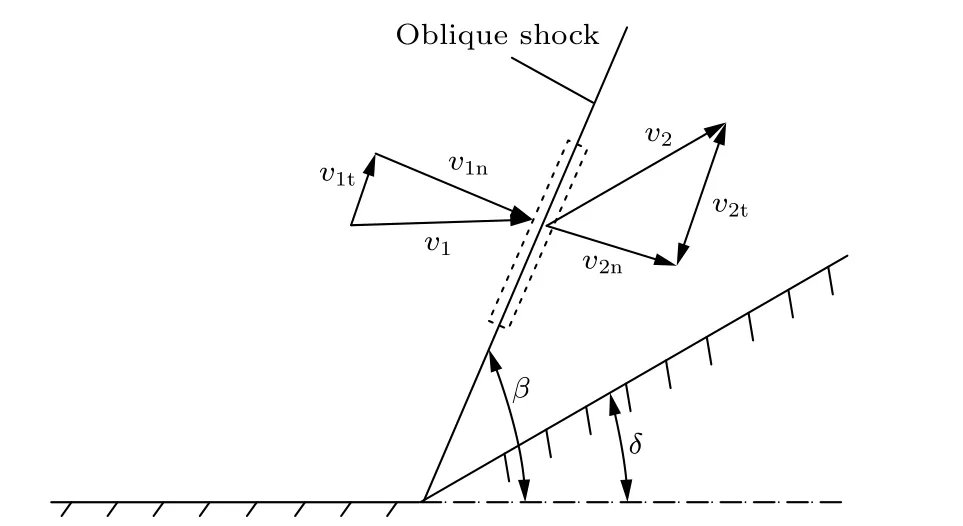
圖15 斜激波波前/波后速度分解示意圖Fig. 15. Schematic diagram of velocity decomposition of oblique shock wave front/back wave.

斜激波波后橫流馬赫數Ma2為

由波后橫流馬赫數Ma2可計算得到波后氣流速度v2,將v2沿水平方向(平行于v1方向)進行分解即得到射流柱前方實際橫流速度ug:

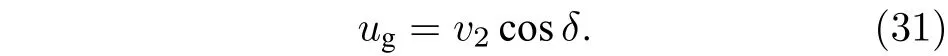
3.3 液體微元質量損失計算

剪切破碎對液體射流一次破碎過程影響較大,只有在特定的韋伯數范圍, 液體射流才會發生剪切破碎[29]. 超聲速橫流一般具有較高的韋伯數, 在剪切力的作用下, 大量的液滴從連續液柱兩側直接剝離, 液柱兩側出現明顯的“拉絲”現象[13]. Mazallon等[31]研究了多種工況條件下液體射流的剪切破碎過程, 并提出了臨界韋伯數的概念, 當橫流氣體的當地韋伯數大于臨界韋伯數, 液體射流便發生剪切破碎.

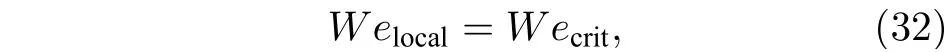
式中Welocal為當地韋伯數;Wecrit為臨界韋伯數,本文Wecrit的值取為100.

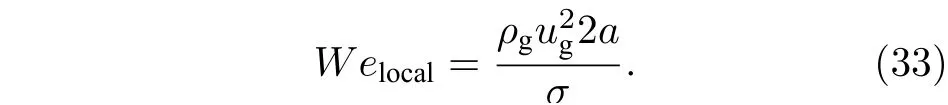
液體微元的質量損失[31]為

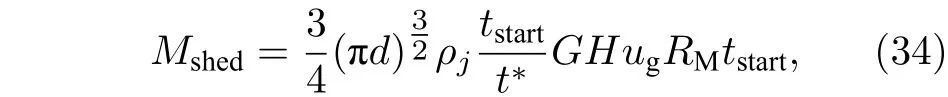
式中,tstart為從表面破碎開始所經過的時間;t?為氣動特征時間,

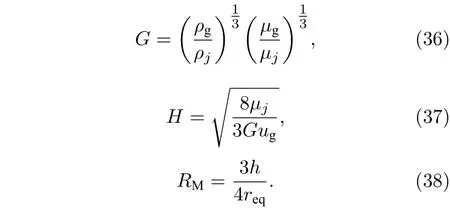
Ranger 和Nicholls[32]以 及Chryssaki 和 Nicholls[33]對于(34)式進行了兩次修正. 第一次修正加入了ts/t?用于控制液體剝離速率, 使剝離速率與離開剝離起點的距離基本呈線性關系; 第二次修正定義了質量比RM,RM為液體微元質量與質量損失的液體質量比值. 本文采用Chryssaki[33]修正后的質量比表達式, 通過液體微元質量間接獲得了沿流向不同位置處剝離液滴的質量, 并將剝離液滴的質量計入橫截面形變方程, 獲得了更為準確的射流軌跡.

基于前文推導, 利用MATLAB 軟件計算了液體射流軌跡和橫截面變形. 采用四階的龍格-庫塔方法求解(13)式、(20)式、(21)式和(23)式, 時間步長為 1 0?6s. 其中, (13)式用于求解連續液柱橫截面形狀(a,b); (20)式和(21)式用于求解液微元質心運動軌跡; (23)式用于求解偏轉角. 理論計算中橫流氣體和液體的工況參數見表3, 主要研究的參數包括: 馬赫數Ma= 2.85/2.1, 噴注壓降1 MPa/1.5 MPa/2 MPa, 噴嘴直徑0.5 mm/1.0 mm, 其中Case 1(d= 0.5 mm)工況為本文基準工況.

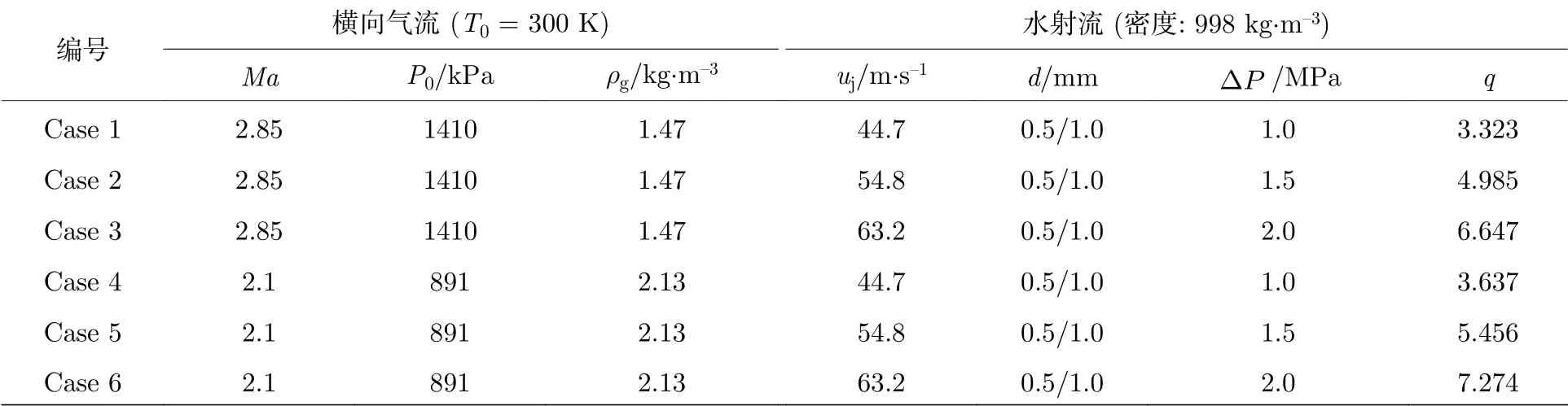
表3 理論計算參數Table 3. Theoretical calculation parameters.

3.4 射流橫截面形變

圖16 為不同噴嘴直徑下射流橫截面橢圓率的計算結果. 從圖16 可以看出, 當橫流馬赫數與噴注壓降保持不變時, 噴嘴直徑越小, 射流橫截面橢圓率變化越快. 這是由于噴嘴直徑減小, 射流流量減小導致射流的慣性越小, 射流更易受橫流氣動力的影響, 故橫截面的變形速度較快. 由于本文計算的橫截面假設為橢圓, 半短軸的長度會在計算過程中不停地減小, 當減小到一定值(絕對值極小)時便已不符合實際液柱斷裂的客觀事實, 依照本文實驗結果截取流向x/d= 2.0 位置作為基準工況下連續液柱橫截面變形終點, 認為超過該位置處的射流開始發生液柱破碎, 同時, 定義液柱有效變形時間tvalid(tvalid=t/t*), 其中t為通過實驗測量得到的液柱破碎時間,t*為氣動特征時間, 通過計算, 本文工況均在tvalid= 0.7 附近發生液柱破碎, 由此認定tvalid= 0.7 為連續液柱結構計算的終點.

圖16 液體微元橫截面橢圓率計算結果Fig. 16. Calculation results of eccentricity of liquid microelement cross section.

圖17 液體微元當地韋伯數計算結果Fig. 17. Schematic diagram of cross-section deformation of liquid microelements.

為了充分考慮剪切破碎對于連續液柱結構建模的影響, 圖17 為液體微元附近當地韋伯數的變化情況. 由(31)式可知, 雖然橫流氣體在經過弓形激波后速度有了一定減小, 但其水平分速度仍然較大, 這導致當地韋伯數較高, 液體微元的原始質量因剪切破碎持續減小. 圖18 為剝離液滴質量與液體微元原始質量的比值隨液柱有效變形時間的變化情況. 從圖18 可以看出, 橫流馬赫數越大, 液滴的剝離量和剝離速度就越大, 基準工況下, 液體微元的剝離質量占比在32%(質量流率為2.8 mg/s)左右.

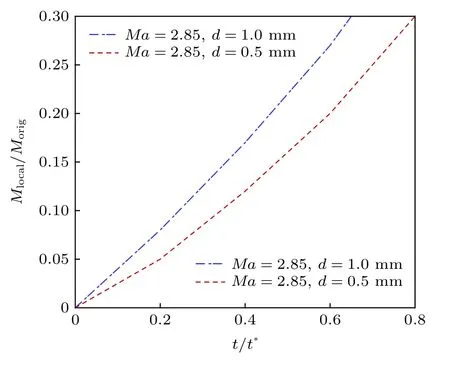
圖18 剝離液滴質量計算結果Fig. 18. Schematic diagram of cross-section deformation of liquid microelements.

3.5 連續液柱模型

圖19為采用CLC 模型對基準工況預測得到的連續液柱結構, 其三維空間上的分布范圍列于表4. 從宏觀上看, 計算得到的連續液柱實體較為符合研究者通過實驗觀測或數值仿真方式得到的射流柱形態; 此外, 計算得到的連續液柱在近噴嘴位置處基本保持完好的圓柱形態, 且隨著流向距離的增加, 連續液柱沿噴注方向的橫截面變得愈發狹窄, 這一點與李春[18]的實驗結果吻合較好. 另一方面, 由于建模過程中忽略了射流柱迎風面的非定常特征, 計算得到的連續液柱的迎風面較為光滑, 這一點與實際破碎過程中連續液柱迎風面特征存在差異, 不過這一差異對氣相流場的時均特性影響較小.

表4 三維連續液柱模型參數Table 4. 3D continuous liquid column model parameters.

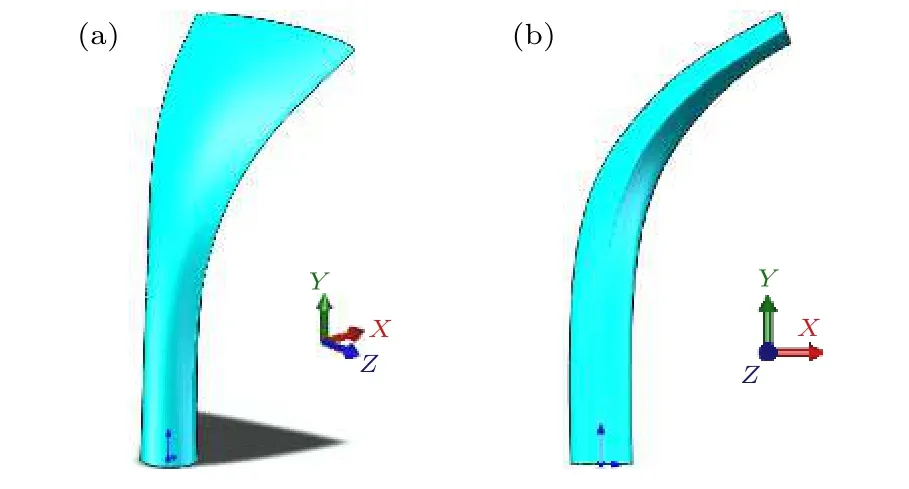
圖19 CLC 模型預測得到的連續液柱結構 (a) 側視圖;(b) 正視圖Fig. 19. Continuous liquid column structure predicted by CLC model: (a) Side view; (b) front view.

4 實驗驗證

本文采用MATLAB 軟件中的圖像邊緣檢測函數獲取近場射流軌跡, 每個工況下提取60 幅瞬態圖像的射流軌跡并進行疊加處理, 結果如圖20所示. 從圖20 中可以看到, 在噴嘴出口, 射流軌跡的脈動范圍很小, 隨著射流逐漸彎曲, 射流軌跡的脈動范圍迅速增大. 此處定義表面波振幅: 取平均射流邊界為基準, 以當地射流軌跡的法向方向取射流振蕩寬度2As作為射流邊界振蕩的幅值, 表面波的振幅即為As. 為方便計算射流軌跡的法線向量,具體計算時取平均射流軌跡(圖中紅色曲線)作為樣本, 采用最小二乘法擬合的邊界線(圖20 中藍色曲線)作為基準計算當地的法向向量, 其中藍色曲線與平均射流邊界擬合的相關系數為0.99.

圖20 射流軌跡疊加結果Fig. 20. Superposition result of jet trajectory.

圖21(a)為超聲速橫向氣流中液體射流柱的顯微成像結果, 由于噴嘴出口附近的射流受到壁面邊界層的影響, 氣體橫流的氣動加速與氣動剪切作用較小, 因此射流柱沒有出現明顯的彎曲變形, 表面波發展不明顯, 液體表面較為光滑, 此處為光滑液柱區域, 即圖中A 區域; 隨著射流進一步穿透橫流氣體, 氣動力的影響顯著增強, 液柱的迎風面開始產生表面波結構, 液柱開始發生彎曲變形, 此處為彎曲液柱區域, 即圖中B 區域; 隨著表面波波長的持續增加(圖21(b)), 液柱斷裂成大尺度液塊并進一步破碎成尺度更小的液塊, 此處為稠密液塊區域, 即圖中C 區域. 具有高時空分辨的顯微成像結果進一步表征了液體射流一次破碎中表面破碎(剪切破碎)、液柱破碎的發生過程與發生順序, 表面破碎發生在彎曲液柱區域與稠密液塊區域, 而液柱破碎發生在彎曲液柱區域結束位置. 圖22 為不同壓降條件下的液體射流近場瞬態顯微圖像. 對比三種不同的壓降條件, 液體射流均存在特征明顯的光滑液柱區域、彎曲液柱區域及稠密液塊區域; 噴注壓降的增大使得液體初始速度增大, 導致液氣動量比增大, 噴嘴出口位置的射流軌跡更高, 連續液柱的彎曲程度更小. 同時, 隨著噴注壓降的增大, 射流迎風面擾動的特征尺度有所減小.

圖23 比較了CLC 模型預測得到的液體射流軌跡結果與本文實驗結果, 從圖23 中可以看出,考慮質量損失后, CLC 模型預測得到射流軌跡結果與實驗結果整體吻合較好, 射流軌跡變得更高,展向寬度也變得更小, 這是由于液滴從連續液柱兩側剝離后, 液柱在噴注方向上橫截面面積變小, 截面變形速度變小, 射流迎風面面積變小, 液體微元所受氣動力相應變小, 故射流可在噴注方向上噴注的更遠; 由于本模型并未考慮射流迎風面變形、破碎情況, 因此, 沿流向各位置處液體微元質量的計算結果偏小, 這使得液體在噴注方向上的動量減小, 因此, 預測得到的射流軌跡較實驗結果偏小.

在亞聲速液體射流中, 液柱破碎位置一般距噴嘴出口較遠. 圖24 給出了研究者們[18,19]總結的亞聲速液體射流液柱破碎的流向位置xb與本文實驗結果. 本文實驗研究工況下, 射流的破碎位置xb=1.0d—2.0d, 明顯小于亞聲速液體射流液柱破碎位置, 這是由于液體射流在超聲速橫流下受到的氣動力更強, 射流液柱破碎位置更加靠近液體噴嘴出口, 同時由于兩相流流場的非定常性, 相同橫流韋伯數下, 液柱破碎位置會在一定范圍內不斷變化.圖25(a)為不同噴注壓降下射流軌跡的計算結果,圖25(b)為不同噴嘴直徑下射流軌跡的計算結果.隨著噴注壓降與噴嘴直徑的增大, 近場射流軌跡彎曲程度減小, 射流穿透深度增強, 計算結果與實驗結果吻合較好, CLC 模型可較好的反映近場射流軌跡的主要變化趨勢和一般規律.

圖21 噴嘴出口位置射流顯微成像結果(基準工況)Fig. 21. Jet microscopic imaging results at the nozzle outlet (basic condition).

圖22 不同噴注壓降射流顯微圖像 (a) ? p = 0.97 MPa; (b) ? p = 1.49 MPa; (c) ? p = 2.05 MPaFig. 22. Microscopic images of jets with different injection pressure drops: (a) ? p = 0.97 MPa; (b) ? p = 1.49 MPa; (c) ? p =2.05 MPa.

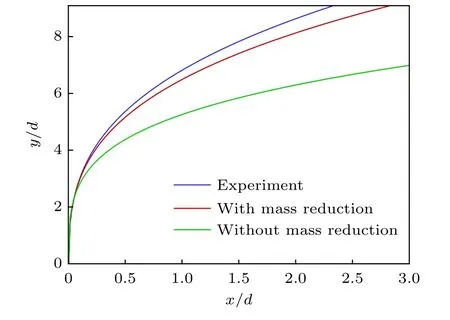
圖23 CLC模型預測得到的射流軌跡結果與實驗結果(基準工況)Fig. 23. Jet trajectory results and experimental results predicted by the CLC model (basic condition).

圖24 超聲速橫流中液柱破碎位置與文獻結果對比Fig. 24. Comparison of the broken position of liquid column in supersonic cross-flow with literature results.

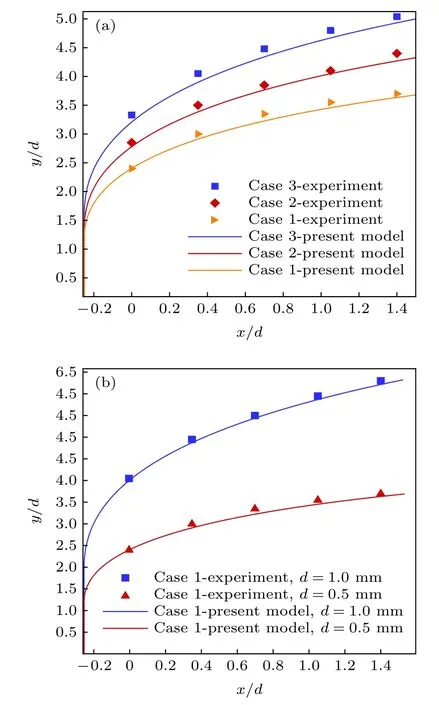
圖25 不同動量比和不同噴嘴直徑下射流軌跡計算結果與本文實驗結果比較(a)d=0.5mm;(b)q=3.32Fig.25.Calcu lations for different mom entum ratios and diffent nozzle diam eters in com parison with experim ents: (a)d=0.5mm;(b)q=3.32.

5 結 論

本文研究了液體射流在超聲速橫流條件下的射流軌跡與連續液柱結構,基于液體微元受力分析推導出了連續液柱橫截面形變方程與微元運動學方程,將二維液滴所受氣動力等效為液體微元所受氣動力,在考慮連續液柱前方弓形激波對流場的影響下,對氣動力進行了修正,并通過質量比描述了連續液柱的質量損失,建立了可定量描述連續液柱時均形態的CLC模型,該模型可較好地預測液體射流軌跡和連續液柱的空間結構.在CLC 模型基礎上,提出了一種基于PIV系統與顯微鏡頭的高時空分辨率顯微成像方法,拍攝得到了近噴嘴區域精細的連續液柱結構并驗證了CLC 模型的準確性.