時(shí)間序列建模的整體流程教學(xué)研究

摘要：時(shí)間序列分析和時(shí)間序列建模是強(qiáng)有力的預(yù)測(cè)工具。理解時(shí)間序列背后的統(tǒng)計(jì)學(xué)知識(shí)對(duì)于時(shí)間序列建模很有幫助。本文將介紹時(shí)間序列的整體流程，包括ARMA 和 ARIMA等重要工具。

時(shí)間序列建模，顧名思義，使用基于時(shí)間的數(shù)據(jù)（年，月，日，小時(shí)，分鐘），然后得出某些預(yù)測(cè)以幫助決策。時(shí)間序列建模在現(xiàn)實(shí)生活中有廣泛的應(yīng)用。雖然要保持與時(shí)間“同步”并做出“預(yù)測(cè)”相當(dāng)困難，但是學(xué)術(shù)界已經(jīng)發(fā)展出一些強(qiáng)有力的工具，我們可以利用他們來(lái)“感知未來(lái)”。時(shí)間序列分析與建模一直以來(lái)都是教學(xué)上的難點(diǎn)和重點(diǎn)，我們可以借助相關(guān)的例子來(lái)對(duì)整個(gè)流程進(jìn)行解析，讓同學(xué)們有更直觀(guān)的認(rèn)識(shí)，然后再具體研究數(shù)學(xué)上的細(xì)節(jié)。

一、ARMA 時(shí)間序列模型

ARMA 是最常用的時(shí)間序列模型。在 ARMA 模型中，AR 代表自回歸 auto-regression，MA 代表移動(dòng)平均 moving average。需要注意的是，AR 或者 MA 模型都不適用于非平穩(wěn)序列。

1.AR 模型

這個(gè)就是 AR（1） 模型的公式。數(shù)值（1）代表下一個(gè)時(shí)刻的值僅僅取決于當(dāng)前的時(shí)刻。alpha 是需要確定的參數(shù)，使得誤差項(xiàng)最小。注意到，x（t-1）也取決于 x（t-2），因此，x（t）將隨著時(shí)間的流逝而漸漸消失。

2.MA 模型

可以注意到，在 MA 模型中，噪聲隨著時(shí)間的消失很快，而在 AR 模型中，突變的影響持續(xù)很久。

3.AR 模型與 MA 模型的區(qū)別

AR 模型與 MA 模型的最大不同在于時(shí)間序列在不同時(shí)間點(diǎn)上的相關(guān)性。對(duì)于 n>階數(shù)的 MA 模型， x（t） 與 x（t-n） 之間的相關(guān)系數(shù)為 0。相關(guān)分析可以得到 MA 模型的階數(shù)。然而，對(duì)于 AR 模型，隨著 n 變大，x（t） 與 x（t-n）之間的相關(guān)性逐漸減少。下面將介紹如何通過(guò)ACF/PACF 確定 ARMA 模型的參數(shù)。

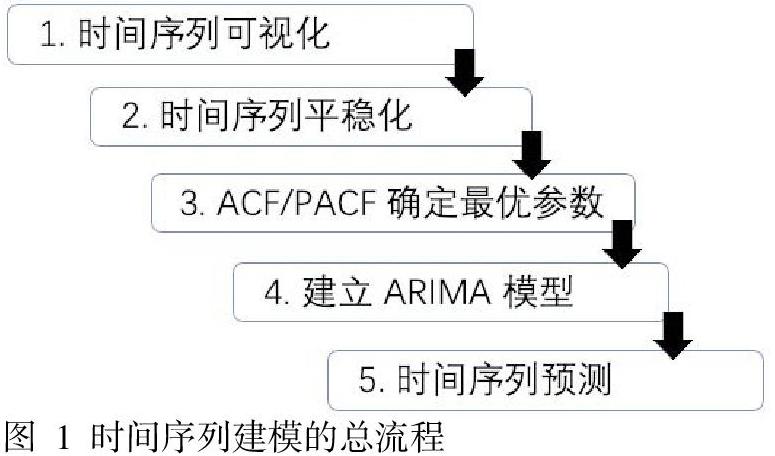
二、時(shí)間序列建模整體流程

第一步：時(shí)間序列可視化。在建立任何時(shí)間序列模型之前，分析序列的趨勢(shì)是關(guān)鍵。我們關(guān)注的趨勢(shì)要包括任何類(lèi)型的趨勢(shì)，如季節(jié)性和某些隨機(jī)行為。

第二步：時(shí)間序列平穩(wěn)化。因?yàn)闀r(shí)間序列的建模過(guò)程中有很多結(jié)論都是建立在大數(shù)定理和中心極限定理的前提條件下的，如果它不滿(mǎn)足，得到的許多結(jié)論都是不可靠的。序列平穩(wěn)，一般要求均值為常數(shù)，方差為常數(shù)，以及自協(xié)方差為常數(shù)。如果一個(gè)序列不是平穩(wěn)的話(huà)，那我們?cè)撛趺崔k呢？有三種常用的方法可以使得時(shí)間序列平穩(wěn)：

1.去除趨勢(shì)：假設(shè)時(shí)間序列的公式是：X（t） = （mean + trend*t） + error。我們可以去掉圓括號(hào)中的部分，然后對(duì)剩余的部分建模。

2.差分：我們可以對(duì)兩項(xiàng)之間的差值進(jìn)行建模，而不是原來(lái)的項(xiàng)。例如：X（t） – x（t-1） = ARMA（p， q）。差分項(xiàng)d可以叫做AR（I）MA模型中的集成項(xiàng)（Integration part）。現(xiàn)在，我們就有了三個(gè)參數(shù)ARIMA（p，d，q）

3.季節(jié)性：季節(jié)性可以很容易地直接融合到 ARIMA 模型中。

一旦我們處理了趨勢(shì)的模式，周期和季節(jié)性等，就可以測(cè)試一下序列是否平穩(wěn)。一個(gè)常用的工具是Dickey-Fuller 算法。

第三步：找出最優(yōu)的階數(shù)。我們可以通過(guò)使用ACF 和 PACF畫(huà)圖找出最優(yōu)的參數(shù)ARIMA（p，d，q）。假如 ACF 和 PACF 都下降緩慢，這預(yù)示著我們需要通過(guò)增加參數(shù) d 的值將序列變平穩(wěn)。

第四步：建立 ARIMA 模型。我們得到ARIMA 的參數(shù)后，就可以開(kāi)始建立模型了。上一步種我們通過(guò) ACF 和 PACF 得到了參數(shù)，但這只是一個(gè)大致的估計(jì)，我們需要遍歷更多的（p，d，q）組合。能得到最低的 BIC值或AIC值的參數(shù)組合將是我們的選擇。假如在 ACF/PACF 畫(huà)圖中發(fā)現(xiàn)季節(jié)性成分，我們也可以納入 ARIMA 的模型中。

第五步：做出預(yù)測(cè)。一旦我們得到最終的 ARIMA 模型，我們就可以對(duì)未來(lái)的時(shí)間點(diǎn)的值做預(yù)測(cè)了。如果模型運(yùn)行良好，我們就可以將趨勢(shì)可視化進(jìn)行交叉驗(yàn)證。

三、實(shí)際應(yīng)用的例子

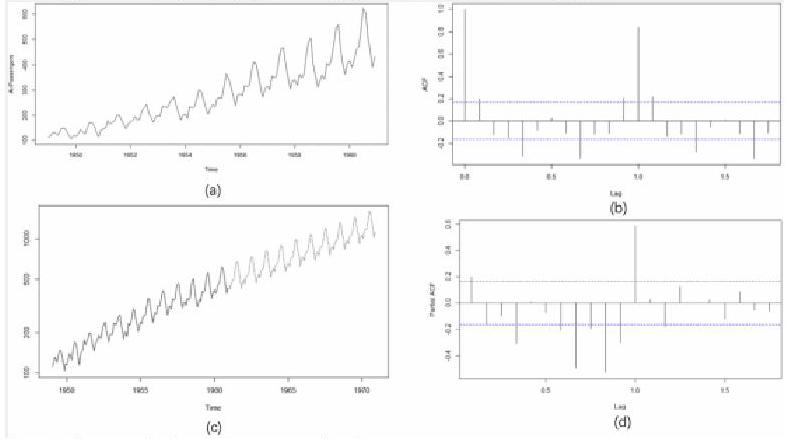
我們可以通過(guò)舉例說(shuō)明時(shí)間序列模型的應(yīng)用。我們使用AirPassengers這個(gè)已有的數(shù)據(jù)集[1]。這個(gè)數(shù)據(jù)集是1949-1960年每個(gè)月國(guó)際航空的乘客數(shù)量的數(shù)據(jù)，如圖2（a）所示。

從圖中，我們可以觀(guān)察出：

1.存在趨勢(shì)成分，隨著時(shí)間的增加而增加;

2.存在季節(jié)性成分，但周期不超過(guò) 12 個(gè)月;

3.數(shù)據(jù)的方差隨著時(shí)間的增長(zhǎng)而增大。

在測(cè)試平穩(wěn)性之前，我們需要解決兩個(gè)問(wèn)題：1）不穩(wěn)定的方差。可以通過(guò)取序列l(wèi)og 對(duì)數(shù)的方法解決。2）季節(jié)成分。這個(gè)可以通過(guò)求序列的差分而實(shí)現(xiàn)。現(xiàn)在，讓我們測(cè)試一下處理后的序列。通過(guò)求 ADF，得到序列的 p-value=0.01。因此，序列是平穩(wěn)的，我們可以對(duì)它進(jìn)行建模。

確定參數(shù)后，我們可以訓(xùn)練 ARIMA 模型，然后預(yù)測(cè)未來(lái)的 10 年的乘客量，將預(yù)測(cè)的結(jié)果可視化，如圖 所示。由于我們是將原始數(shù)據(jù)求對(duì)數(shù)以及再一階差分進(jìn)行處理，因此我們的預(yù)測(cè)要有復(fù)原的過(guò)程。至此，一個(gè)完整的ARIMA 時(shí)間序列建模預(yù)測(cè)過(guò)程就完成了。

參考文獻(xiàn)

[1] https：//www.kaggle.com/rakannimer/air-passengers

作者簡(jiǎn)介：羅曉牧（1980-），性別：男，廣東省廣州市（籍貫），現(xiàn)職稱(chēng)：副教授，學(xué)歷：工科博士研究生畢業(yè)，研究方向：機(jī)器學(xué)習(xí)，無(wú)線(xiàn)傳感器網(wǎng)絡(luò)，生物信息獲取.

基金來(lái)源：廣州中醫(yī)藥大學(xué)教學(xué)改革項(xiàng)目 A3-0433-181-427-039