基于加權網格和信息熵的并行密度聚類算法*

胡 健，徐鍇濱，毛伊敏+

1.江西理工大學信息工程學院，江西贛州341000

2.江西理工大學應用科學學院信息工程系，江西贛州341000

1 引言

聚類算法是一種無監督的學習算法，能夠根據數據對象的相關特征，將相似的對象歸為一類，而差別較大的數據對象則劃分到不同類中，因此聚類算法可以從樣本數據中發現潛在的分布模式，被廣泛應用于文本分析、生物學、醫學、衛星圖像分析等各種領域[1]。在聚類算法中，基于密度的聚類算法，如DBSCAN[2]（density-based spatial clustering of applications with noise）和OPTICS[3]算法，可以發現任意形狀的簇且對噪聲不敏感，受到人們的廣泛關注[4-6]。

隨著互聯網信息技術的不斷發展以及大數據時代的到來，使得大數據相較于傳統數據，具有了4V特性[7]——Volume（數量大）、Variety（種類多）、Velocity（速度快）、Value（價值密度低）。但是傳統的密度聚類算法所需的時間復雜度較高，只適用于較小規模的數據集，而在處理大數據時無疑會產生更龐大的計算復雜度[8]。因此，如何降低密度聚類算法的計算復雜度，將其應用到大數據上，是個具有挑戰性的難題。

隨著Google開發的MapReduce架構的廣泛應用，以Hadoop、Spark為代表的分布式計算架構受到了越來越多的關注[9-10]。為了能進一步降低密度聚類算法的計算復雜度，通過改進傳統的密度聚類算法，并與分布式計算架構相結合成為目前密度聚類算法研究的主要方向[11-14]。Li等人[15]首先提出了基于Map-Reduce下的并行DBSCAN算法，其使用MapReduce計算架構，將數據分片后并行執行DBSCAN算法形成局部簇，再通過增量的方式合并得到全局簇，實現了DBSCAN算法的并行化，然而該算法沒有提出有效方法來劃分數據，合并局部簇的計算復雜度較高。Silva等人[16]提出了MapReduce下的分布式DBSCAN算法，根據特定場景劃分數據，聚類簇的合并采用增量的方式，算法的時間復雜度較高，算法總體并行化效率較低。文獻[17-18]分別提出了基于Hadoop和基于Spark下的并行密度聚類算法，有效降低密度聚類算法的計算復雜度，同時分別給出了基于Hadoop和Spark下的數據劃分方案，但算法對數據進行分區處理時未具體考慮數據特性，也沒有給出有效的局部簇合并生成全局簇的方法。

如何有效地劃分數據，合并局部簇一直是密度聚類算法并行化的重要研究內容[19]。由于數據網格化能將空間數據劃分為有限數目的單元，落入同一網格的點可以被看作一個對象進行處理，可以很好地解決數據劃分的問題[20]。因此，He等人[21]提出MRDBSCAN（efficient parallel density-based clustering algorithm using MapReduce）算法，采用均勻劃分網格的方式將數據網格化，以網格單元作為對象并行執行DBSCAN算法，最后合并這些網格對象得到全局簇。然而算法明顯存在兩個問題：均勻劃分網格時，網格單元的大小實際難以確定，算法的聚類效果受網格單元大小的影響較大，導致算法的聚類效果不佳；另外，算法在合并局部簇時采用增量的方式，計算效率仍然較低。在此基礎上，文獻[22-23]分別提出了基于Hadoop下的H-DBSCAN算法和基于Spark下的S-DBSCAN算法，同樣是采用均分網格的方法來劃分數據，不同的是它們通過加入網格邊界的擴展，以此來提高聚類結果的精確度和局部簇的合并效率。為了能更有效地劃分網格，以及進一步加快合并局部簇的效率，王興等人[24]提出增量并行化快速聚類算法IP-DBSCAN（incremental parallelization of fast clustering based on DBSCAN algorithm）。該算法主要分為三個階段：首先通過二分法和貪心算法對空間數據進行合理網格化；其次進行本地局部聚類，獲得局部簇候選集；最后使用R*-tree索引策略進一步提高局部簇的合并速度。相較于其他按網格劃分數據的并行密度聚類算法，IP-DBSCAN算法能更加合理地對數據進行劃分，且在合并局部簇時加快了收斂速度，從而進一步加快了算法的并行化效率。然而該算法仍存在兩個明顯的不足：一方面，算法采用二分法劃分數據時，仍需要輸入網格邊長閾值，閾值的不同會影響算法的聚類結果準確度，導致聚類結果的準確度不高；另一方面，在進行本地局部聚類時計算復雜度較高，在合并局部簇時沒有采用并行化的思想，算法總體并行化效率有待進一步提升。針對上述算法存在的問題，本文主要做了以下幾方面工作：（1）在數據劃分階段，根據空間中數據點的分布狀況，提出ADG（adaptive division grid）策略來自適應劃分網格。（2）在完成數據劃分之后，為提高局部聚類效果，針對每個數據分區，提出NE（neighboring expand）策略構建其加權網格用于加強網格之間的關聯性；同時提出WGIE（weighted grid and information entropy）策略來計算網格密度以及密度聚類算法的ε鄰域和核心對象，使密度聚類算法更適用于加權網格；最后為解決并行密度聚類算法對局部簇的計算效率較低的問題，提出基于MapReduce的并行局部簇聚類算法COMCORE-MR（core clusters computing algorithm based on MapReduce）。（3）在局部聚類完成后，為進一步加快局部簇合并的收斂速度，提出了基于并查集的局部簇合并算法MECORE（merge core cluster）；接著結合MapReduce計算模型，提出了基于MapReduce的并行化合并局部簇算法MECORE-MR（merge core cluster by using MapReduce），實現并行化合并局部簇，從而進一步提升算法總體并行化效率，更快地獲取聚類結果的全局簇，提升了并行密度聚類算法對局部簇合并效率。

2 算法及相關概念介紹

2.1 加權網格

加權網格[20]表示為WG=(G,N(G),W)，其中G=gi表示一個網格單元，N(G)=N(gi)表示與網格單元gi相關聯的其余網格單元集合，W=w(gi,N(gi))表示網格單元gi與其余網格單元的權值。

2.2 均勻網格劃分

均勻網格劃分[25]的思想是：對于給定的數據空間，其維度為D，則將每一維的數據分成n個具有相同大小且互不相交的區間，因此D維數據空間就被劃分為nd個相等的網格單元。如圖1所示，若D=2，n=3，則該二維數據空間被劃分為9個相等的網格單元。

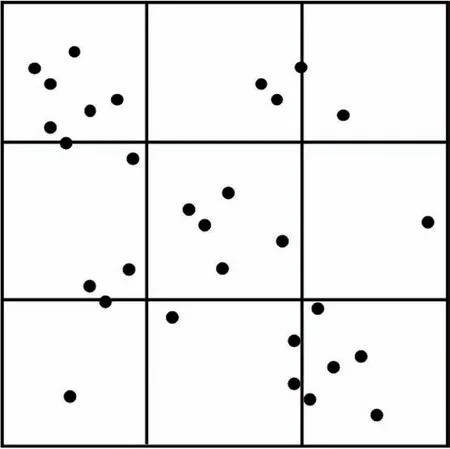
Fig.1 Uniform grid division圖1 均勻網格劃分

2.3 信息熵

對于一個離散型的變量X，其信息熵[26]公式為：

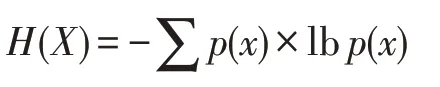
其中，p(x)為離散變量X在系統事件中出現的概率。

2.4 并查集

并查集[27]用一棵單獨的樹表示每一個集合，樹的根節點表示該集合的代表，樹的每個葉子節點表示集合中的一個元素。對于一組不相交的動態集合X={x1,x2,…,xn}和Y={y1,y2,…,yn}，利用并查集對其進行合并一般分為三個步驟：

makeset(X,Y)階段：分別將集合X和集合Y建立一個新的并查集，其中包含n個單元素集合。

find(x)階段：返回元素x所在集合的代表。

unionset(x,y)階段：若元素x和元素y所在的集合不相交，則合并x和y所在的集合。

3 DBWGIE-MR算法

3.1 算法思想

DBWGIE-MR（density-based clustering algorithm by using weighted grid and information entropy based on MapReduce）算法的思想是：（1）根據數據點空間分布狀況，提出ADG策略來自適應劃分網格。（2）對每個數據分區，提出NE策略構建其加權網格用于加強網格之間的關聯性，以此提高聚類效果；同時提出WGIE策略來計算網格密度以及密度聚類算法的ε鄰域和核心對象，使密度聚類算法更適用于加權網格；最后結合MapReduce計算模型，提出并行的局部簇聚類算法COMCORE-MR，解決并行密度聚類算法對局部簇的計算效率較低的問題，從而提升算法的總體并行化效率。（3）在局部簇生成后，基于并查集的合并方法，提出了基于并查集的局部簇合并算法MECORE，用于加快合并局部簇的收斂速度；接著結合MapReduce計算模型，提出了基于MapReduce的并行化合并局部簇算法MECORE-MR，實現并行化合并局部簇，從而進一步提升算法總體并行化效率，實現了并行化地合并局部簇，從而更快地得到聚類結果的全局簇，提升了基于密度的聚類算法對局部簇合并的效率。

3.2 數據劃分

目前基于網格劃分數據的并行化密度聚類算法中，對于網格的劃分往往是采用均勻劃分的方式，即在數據的某一維度上進行等分，這種劃分方式存在兩個缺陷：（1）網格邊長選取的不確定性，即劃分數據時網格的初始邊長難以確定，邊長大小的選取對于聚類效果的影響較大；（2）網格數據密度不一致性，即在數據網格化時未考慮大數據環境下數據的分布特性，導致劃分后的網格數據密度存在不均勻的情況。針對這些問題，本文提出了ADG策略用于將數據自適應地劃分為網格。ADG策略的描述如下：

先將d維數據空間等分為2d個初始網格單元，再根據網格中數據點之間分布狀況來計算網格邊長的劃分閾值φ。當所有網格滿足非空且當前邊長大于劃分閾值時，則停止網格劃分。網格邊長劃分閾值φ的取值需要根據當前最小網格中的點個數和數據點分布的緊密程度，當網格單元中的數據點個數過多或者分布過于稀疏，則需要進一步劃分網格，而數據點之間的最小平均距離可以體現當前網格中整體數據分布的狀況，故閾值φ的計算公式如下：

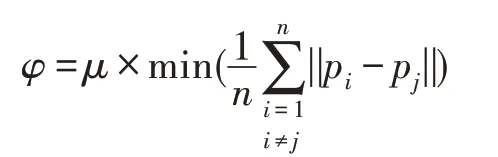
其中，pi和pj分別為d維空間中的任意兩個數據點，μ為當前最小網格單元中的點個數。

ADG策略首先將整體空間劃分為大小相同的數據網格，再對每一個網格做進一步細分，故其特點是將均勻網格劃分與自適應網格劃分相結合，從全局上數據網格的劃分是非均勻的，而從局部上數據網格呈現的是均勻劃分的狀態。此外，由于ADG策略綜合考慮了每個網格單元的數據點的數量及其分布特性，通過計算密度閾值，能對數據點較多的網格單元做進一步的細分，直到每個數據網格均滿足密度閾值才會停止劃分，因此最后得到的網格單元密度較為均勻，這樣保證了算法計算節點的負載平衡，也為局部聚類的算法穩定性提供了保障。

3.3 局部簇形成

目前基于網格劃分的并行化密度聚類算法中，局部簇的形成是通過在每個網格對象中并行執行聚類算法獲得的，這種方式存在兩個問題：一是在聚類過程中未能充分考慮到相鄰網格之間數據的關聯性，導數聚類效果不好；二是算法的計算復雜度較高，對局部簇的計算效率較低。針對這些問題，本文首先基于鄰居網格和網格邊界擴展原理，提出NE策略來構建每個數據分區的加權網格，加強網格之間的關聯性，以此來提高聚類效果；同時，提出WGIE策略來計算網格對象的密度值，并重定義ε鄰域和核心對象，使密度聚類算法更適用于加權網格；最后結合MapReduce計算模型，提出并行的局部簇聚類算法COMCORE-MR，解決并行密度聚類算法對局部簇的計算效率較低的問題，以此來提升算法的總體并行化效率。

3.3.1 加權網格構建

在對數據進行網格化處理后，為了能在聚類過程中考慮到相鄰網格之間數據的關聯性，進一步提升聚類效果，本文提出了NE策略來構建每個數據分區的加權網格，加強網格之間的關聯性，以此來提高聚類效果。NE策略的描述如下：

首先對加權網格的作用范圍進行設置。為更好地確定加權網格的作用范圍，基于網格對象的鄰居網格[28]，加權網格的作用范圍定義如下：

NE策略通過構建每個網格對象的加權網格，使得算法在對每個網格對象進行局部聚類的過程中，不再是單一地考慮每個網格對象內部的數據關系，而是能根據每個網格對象的加權網格，綜合考慮了相鄰網格簇之間的連通關系以及權重關系。這樣既避免了算法容易陷入局部最優，同時提高了聚類結果的精確度。

例1如圖2所示，在該數據網格中有16個網格單元，數據的維度為2。

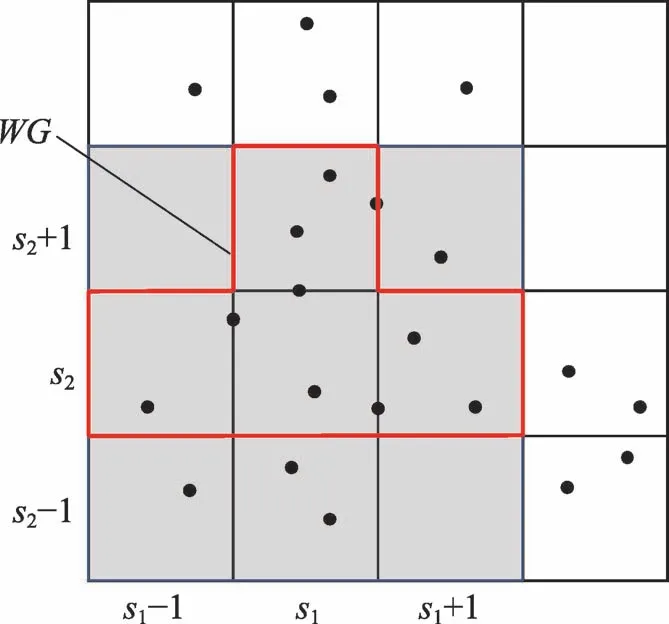
Fig.2 Construction of weighted grid圖2 加權網格的構建

3.3.2 網格密度的計算

目前基于網格劃分的并行化密度聚類算法中，網格密度的計算是使用網格中的數據點個數作為該網格對象的密度值，雖然這種密度表示方法在大多數基于密度的聚類問題中取得了較好效果，但在基于加權網格的密度聚類問題中，由于不同網格對象之間存在著關聯性，因此直接使用網格中的數據點個數來計算加權網格中的網格密度，有失合理性。在構建好網格對象的加權網格之后，為使密度聚類算法能更好地應用于加權網格，本文提出WGIE（加權網格信息熵）策略用于計算網格單元的密度，并重新定義密度聚類算法的ε鄰域和核心對象。WGIE策略定義如下：

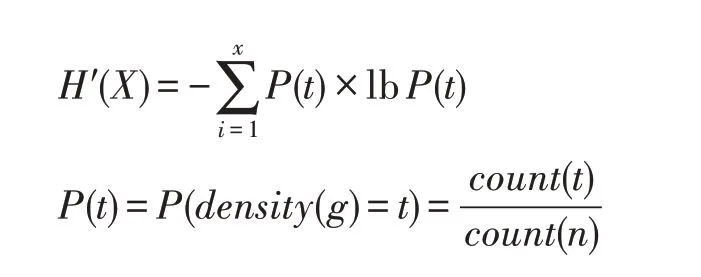
其中，t表示數據網格化后的某一非空網格單元的密度，即以該網格單元為中心構成的加權網格中的所有數據點個數；x表示該密度取值下的網格單元數量；P(t)是網格單元密度為t所出現的概率；count(t)表示網格單元中網格密度為t的網格單元個數；count(n)表示劃分后的非空網格單元總數。

證明（1）單調性：對于?t1,t2且t1-t2＞0，P(t1)-P(t2)＞0，則H′(P(t1))-H′(P(t2))＜0。

（2）非負性：因為0 ＜P(t)，lbP(t)＜0，所以0 ＜，即H′(X)＞0。

（3）累加性：對于?t1,t2∈t，H′(P(t))=H′(P(t1,t2))=H′(P(t1)×P(t2))=H′(P(t1))+H′(P(t2))。

因此公式滿足信息熵定義的基本條件，是系統穩定程度的度量公式。□

為使密度聚類算法更好地應用于加權網格，根據加權網格的作用范圍和加權網格信息熵策略來重定義ε鄰域和核心對象。核心對象與網格單元的密度值密切相關，采用加權網格與信息熵策略能有效刻畫加權網格中網格對象的密度值，當網格單元的密度H′(X)小于給定的密度閾值μ時，則說明以該網格單元為中心的加權網格中的數據是比較有序的，因此執行聚類算法的過程中以該網格單元作為中心效果會更好，該網格單元中成為核心對象的概率越大。ε鄰域和核心對象定義如下：

定義1（加權網格的ε鄰域）對于一個網格對象gi，以該網格對象為中心構建加權網格后，加權網格范圍內的所有網格對象為網格對象gi的ε鄰域。

定義2（加權網格的核心對象）對于一個網格對象gi，若其密度滿足H′(X)≤μ（即加權網格信息熵小于給定的閾值），則該網格對象為核心網格對象。包含在核心網格內的任一點均為核心對象。

3.3.3 局部聚類

在提出了網格對象的密度計算方法之后，為了能更快地進行局部聚類，進一步加快算法的總體并行化效率，本文提出基于MapReduce的并行化計算局部簇的COMCORE-MR算法。該算法主要分為兩個階段，并行計算網格密度階段和并行計算局部簇階段。

先在并行計算網格密度階段，需要輸入網格對象g以及網格中的點pi；接著，執行map函數計算出以網格對象g為中心的加權網格中點的數量Ci[g]，并輸出Key-value值＜g,Ci[g]＞。之后，執行reduce函數合并map函數的結果，并使用WGIE策略計算出每個網格對象的網格密度hi，最后輸出Key-value值＜(g,N(gi)),hi＞傳入下一個階段。如圖3（a）所示。

接著在并行計算局部簇階段，需要輸入數據集D中的點pi以及上個階段計算出的Key-value值＜(g,N(gi)),hi＞；之后，調用map函數對數據進行計算，如果輸入的數據為數據點pi，則map函數計算每個數據點所對應的網格對象g并輸出Key-value值＜g,pi＞，如果輸入的數據為Key-value值＜(g,N(gi)),hi＞，則map函數根據定義2計算當前網格對象g是否為核心網格，如果hi≤μ，則當前網格對象g為核心網格，輸出Key-value值＜g,N(gi)＞，如果hi＞μ，則不輸出任何結果；最后執行reduce函數，合并map函數的結果，輸出Key-value值＜(g,N(gi)),N(pi)＞。最終得到的結果便是核心簇的序列集合，即聚類結果的局部簇。如圖3（b）所示。

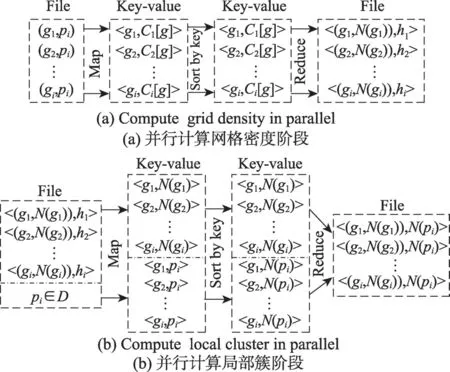
Fig.3 Process of COMCORE-MR algorithm圖3 COMCORE-MR算法的計算過程

3.4 局部簇的合并

目前基于網格劃分的密度聚類算法中，對局部簇的合并通常是采取增量的方式，并且沒采取并行化思想，導致算法在合并局部簇時計算復雜度較高，算法總體并行化效率較低。針對這些問題，本文首先提出了基于并查集的局部簇合并算法（MECORE），用于加快合并局部簇的收斂速度；接著結合MapReduce計算模型，提出了基于MapReduce的并行化合并局部簇算法（MECORE-MR），實現并行化合并局部簇，從而進一步提升算法總體并行化效率。

3.4.1 局部簇的合并

為進一步加快合并局部簇的收斂速度，本文提出了基于并查集的合并局部簇算法（MECORE），該算法首先基于并查集對兩個不相交集的合并方法，提出了基于并查集的合并不同網格對象的3個方法：Makeset、Find、Unionset。Makeset方法先將每個不同的網格對象單獨處理為一個樹葉節點；Find方法將處于同一局部簇中的網格對象節點相連接，返回一棵以根節點為代表的樹，簇的核心網格對象作為根節點，而局部簇中的其他網格對象作為葉節點，所有的葉節點都與根節點連接；Unionset方法是將兩個不同的局部簇進行合并，尋找共同的葉子節點，將其中一棵樹的根節點轉換為另一棵樹的葉子節點。接著使用這3個方法對局部簇進行合并。算法的總體步驟如下：

對于所有的局部簇對象，將這些局部簇對象所構成的表R作為合并局部簇算法的輸入，表的每一項都是核心網格對象g以及核心網格的鄰域N(g)。首先，算法初始化每一個非空網格對象g∈G，將其看作一個單獨的簇，每一個網格對象的狀態都被初始化為unvisited，并且在算法執行之后每個網格對象的狀態將變為unvisited、non-core和core這3個狀態之一。接著，在輸入局部簇所構成的表后，算法檢索每一個核心網格對象g的Key-value值＜g,N(gi)＞，將其狀態由unvisited更改為core，之后要對其鄰域內的網格對象N(g)的狀態進行設置，分為以下幾種情況：

如果在N(g) 中的一個網格對象gi的狀態為non-core，則表示當前的網格對象gi已經分配到了另一個簇中，因此網格對象gi的狀態保持不變。

如果在N(g)中的一個網格對象gi的狀態為core，則將以gi為核心的局部簇合并到g的局部簇中。

如果在N(g) 中的一個網格對象gi的狀態為unvisited，則將其加入到以g為核心的局部簇中，并將gi的狀態變更為non-core。

最后，在算法執行完之后，根據數據點和網格ID的相對應，便能得到聚類的全局簇，而被標記為unvisited的網格對象中的數據點便是離群點(outlier)。

算法具體實現如下：

3.4.2 局部簇的并行化合并

基于并查集的局部簇合并算法可以很好地對局部簇進行合并得到聚類的全局簇。為了進一步提高合并局部簇的效率，解決基于密度的并行化聚類算法中沒有并行化合并局部簇的問題，本文提出了基于MapReduce的并行化合并局部簇的MECORE-MR算法。MECORE-MR算法的步驟如下：

算法需要將網格對象集G、數據集D以及表R作為輸入，其中表R中的數據是COMCORE-MR算法計算出的局部簇數據。該算法首先隨機地將網格對象集合G劃分為數量相近的k個部分G1,G2,…,Gk，同時將表R也劃分為k個部分R1,R2,…,Rk，其中k的值對應了執行算法所需要的并行節點數；接著，執行map函數，如果map函數輸入的數據為數據點pi∈D，則map函數計算每個數據點所對應的網格對象g并輸出Key-value值＜g,pi＞；如果輸入的數據為表R中的局部簇數據，則檢索該局部簇的核心網格對象的Key-value值＜g,N(gi)＞,根據Key值g在G1,G2,…,Gk中進行索引，得到相應的k值，將此核心網格對象的Key-value值分配到相應的Rk中，并輸出Key-value值＜Mi,(g,N(gi))＞傳遞到reduce函數中去；最后執行reduce函數，對于每個Mi，并行化執行MECORE算法，將得到的k個合并結果最后執行一次局部簇合并算法，再與＜g,pi＞進行結合得到聚類全局簇。

在MECORE-MR算法中，通過并查集結構對局部簇進行合并的時間復雜度為O(i×n)，其中n為數據點個數，i為核心網格對象中點的極大值，因此其時間復雜度趨近于常量。考慮到大數據環境下，n的值較大，通過結合MapReduce可以進一步降低其時間復雜度，有效提升對局部簇的合并效率。

算法具體實現如下：

3.5 DBWGIE-MR算法的步驟

DBWGIE-MR算法具體實現步驟如下所示：

4 實驗結果以及分析

4.1 實驗環境

為驗證DBWGIE-MR算法的性能，本文設計了相關實驗。實驗的硬件設備為Master主機1臺和Slaver機3臺，共4個節點。每一臺硬件設備的處理器均為Intel?CoreTMi5-9400H CPU@2.9 GHz，內存16 GB。實驗的軟件編程環境均為python3.5.2；操作系統均為Ubuntu 16.04；MapReduce架構均為Apache Hadoop3.2版本。

4.2 數據來源

DBWGIE-MR算法實驗數據為4個人工合成的類簇，分別是Flame、Compound、Aggregation和D31。Flame[29]是一個包含凸數據集和凹數據集的密度簇，包含240個樣本點，如圖4（a）所示；Compound[30]是一個擁有6個不同形狀的復雜結構密度簇，共有399個樣本點，這些簇之間存在著相連、內嵌、包含和不同密度重疊的情況，如圖4（b）所示；Aggregation[31]擁有7個不同形狀的非高斯分布的密度簇，共有788個樣本點，如圖4（c）所示；D31[32]則擁有31個高斯密度簇，如圖4（d）所示。

4.3 評價指標

為驗證DBWGIE-MR算法對數據集的聚類精確度，采用F-measure對聚類算法的結果進行評價，Fmeasure是正確率(precision)和召回率(recall)的加權平均值，計算方法如下：

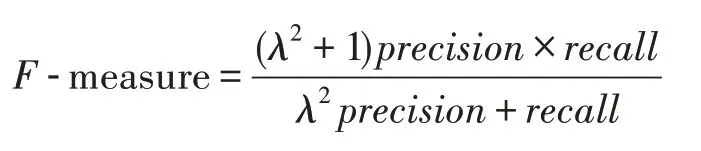
通常情況下，參數λ設置為1，F-measure綜合考慮了聚類結果的正確率（precision）和召回率（recall）的情況，能夠較為準確地評價聚類算法的結果，當Fmeasure的值較高時，說明聚類結果更為準確合理。

4.4 參數選取

DBWGIE-MR算法通過使用ADG策略，自適應劃分數據空間，并且使用NE策略和WGIE策略來計算網格對象的密度值，但對于密度閾值μ來說，仍需要指定具體的值。為了使DBWGIE-MR算法能獲得更加準確的聚類結果，需要對密度閾值μ的取值進行合理的設置，本文在基于Flame數據集下，保證其他參數不變，將密度閾值μ的取值設置為[1,12]，獨立運行10次，取10次的F-measure均值進行分析。從圖5中可以看出，密度閾值μ的值給定得太小或者太大都會影響聚類結果的準確度。實驗結果表明，在μ的值取5的時候，能得到較為準確的聚類結果。

4.5 NE策略和WGIE策略的有效性分析

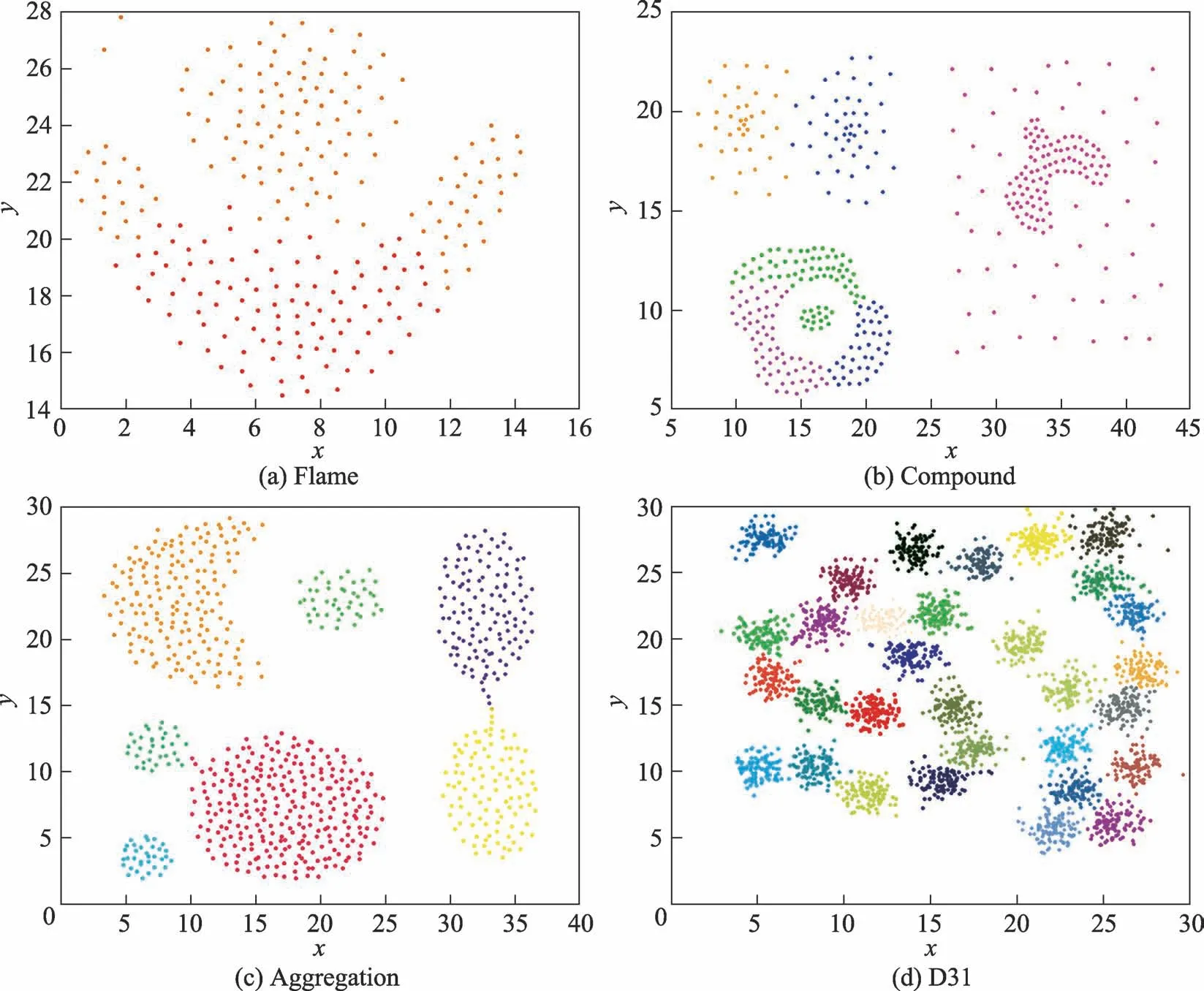
Fig.4 Dataset of experiment圖4 實驗數據集

Fig.5 Selection of density value圖5 密度閾值的選取

為驗證NE策略和WGIE策略進行局部聚類的有效性，實驗中利用本文算法DBWGIE-MR，分別采用不同的局部聚類方式，比較在不同聚類數目下的Fmeasure值的變化。將MR-DBSCAN[21]、H-DBSCAN[22]算法中的局部聚類方法與本文的基于NE策略和WGIE策略的局部聚類方式進行對比實驗，圖6為運行次數在[0,10]范圍內變化時，分別采用3種不同的局部聚類方式的聚類效果。

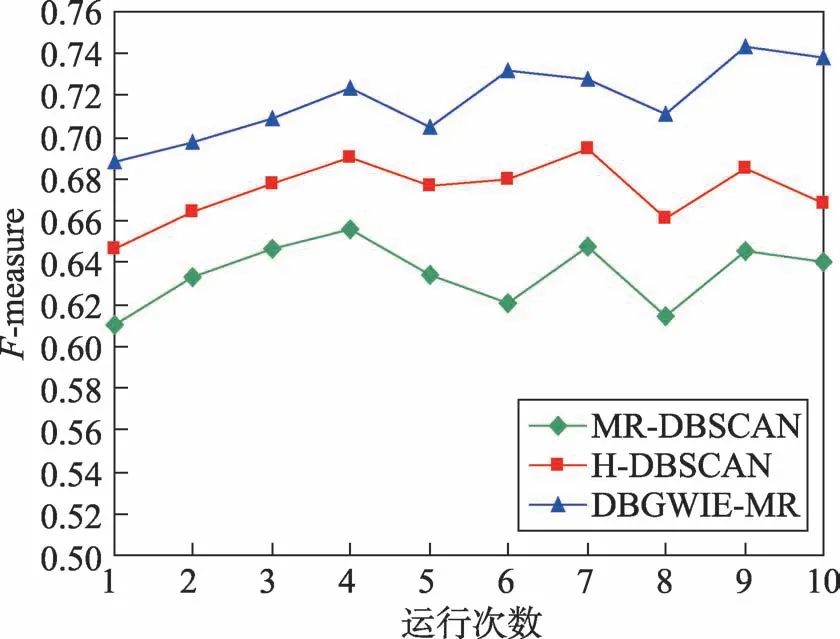
Fig.6 Comparison of results in different local cluster algorithms圖6 不同局部聚類方式下的聚類效果比較

從圖6中可以看出，本文通過NE策略和WGIE策略，以加權網格的方式進行局部聚類的效果明顯優于采用MR-DBSCAN和H-DBSCAN算法的局部聚類方式。當采用這3種不同的局部聚類方式的聚類效果相差最大時，DBWGIE-MR算法使用基于NE策略和WGIE策略的方式進行聚類時，F-measure要比采用MR-DBSCAN和H-DBSCAN算法的局部聚類方式分別高出17.8%和8.3%。由于MR-DBSCAN的局部聚類過程是在單一的網格單元中進行，使得聚類過程僅考慮到網格對象內部的數據關系，而孤立了不同網格中的數據關系，這種局部聚類方式考慮得不夠全面，比較單一，容易使算法陷入局部最優，因此其F-measure值相對較低。H-DBSCAN算法的局部聚類方式是建立在MR-DBSCAN基礎上，在單一的網格單元中進行局部聚類之后，再根據網格之間的共同邊界點，對網格邊界進行二次擴展，考慮了相鄰網格簇之間的連通關系，因此其F-measure值優于MR-DBSCAN。但是這種改進方式是在每個網格單元完成局部聚類之后再進行重聚類，其聚類效果有待進一步提升。而DBWGIE-MR算法采用NE策略和WGIE策略，構建了每個網格對象的加權網格，并以加權網格的聚類方式，在局部聚類的整個過程中綜合考慮了相鄰網格簇之間的連通關系以及權重關系，對網格簇之間的關系分析得較為全面，因此采用NE策略和WGIE策略進行聚類的效果較好。

4.6 聚類結果的比較分析

為驗證DBWGIE-MR算法聚類結果的精準度，本文在基于Flame、Compound、Aggregation和D31的數據集下進行實驗，根據聚類結果的最優值、精確度、方差和運行時間，分別與MR-DBSCAN[21]算法和H-DBSCAN[22]算法的性能進行綜合比較。聚類結果的最優值能夠反映算法尋優能力的強弱程度，值越小表示尋找局部簇的能力越強；精確度可直觀地反映算法聚類結果的好壞程度；運行算法20次得到聚類結果的方差能夠表示算法的穩定程度，值越小表示算法越穩定；運行時間表示得到聚類結果所花費的時間。實驗結果如表1所示。

從表1中可以看出，MR-DBSCAN算法的聚類效果較差，而H-DBSCAN算法的聚類效果比MRDBSCAN算法的聚類效果更好，尤其是在Flame數據集上精確度提升了0.046。因為其在數據網格化的基礎上加入了對網格邊界點的處理，在一定程度上克服了MR-DBSCAN算法沒有考慮網格之間關聯性的缺陷，具有一定的尋優能力。但由于采用的是均分網格的數據網格化方法，沒有考慮到數據點的分布狀況，因此H-DBSCAN算法的穩定性均不佳。而DBWGIE-MR算法在穩定性的表現上比MR-DBSCAN和H-DBSCAN算法更佳，說明DBWGIE-MR克服了以上算法的缺陷，采用ADG策略自適應地將數據劃分為密度較為均勻的網格單元，保證了數據網格化的合理性，對算法計算節點的負載平衡起到一定的幫助，算法聚類過程的波動性較低，因此算法穩定性更好，DBWGIE-MR算法的方差較低；與此同時，通過采用NE策略以及WGIE策略構建加權網格以及形成加權網格的局部聚類方式，使得局部聚類的過程中能綜合考慮到不同網格對象之間的關聯度，避免了算法陷入局部最優，使得DBWGIE-MR算法具有較強的尋優能力，因此DBWGIE-MR算法的最優值最小；此外，DBWGIE-MR算法的運行時間比起MRDBSCAN和H-DBSCAN算法，在Flame數據集上分別降低了0.47 s和0.89 s，原因是DBWGIE-MR算法采用了并行化合并局部簇算法MECORE-MR算法，加快了合并局部簇的收斂速度，因此DBWGIE-MR算法對聚類過程的執行速度得到提升。

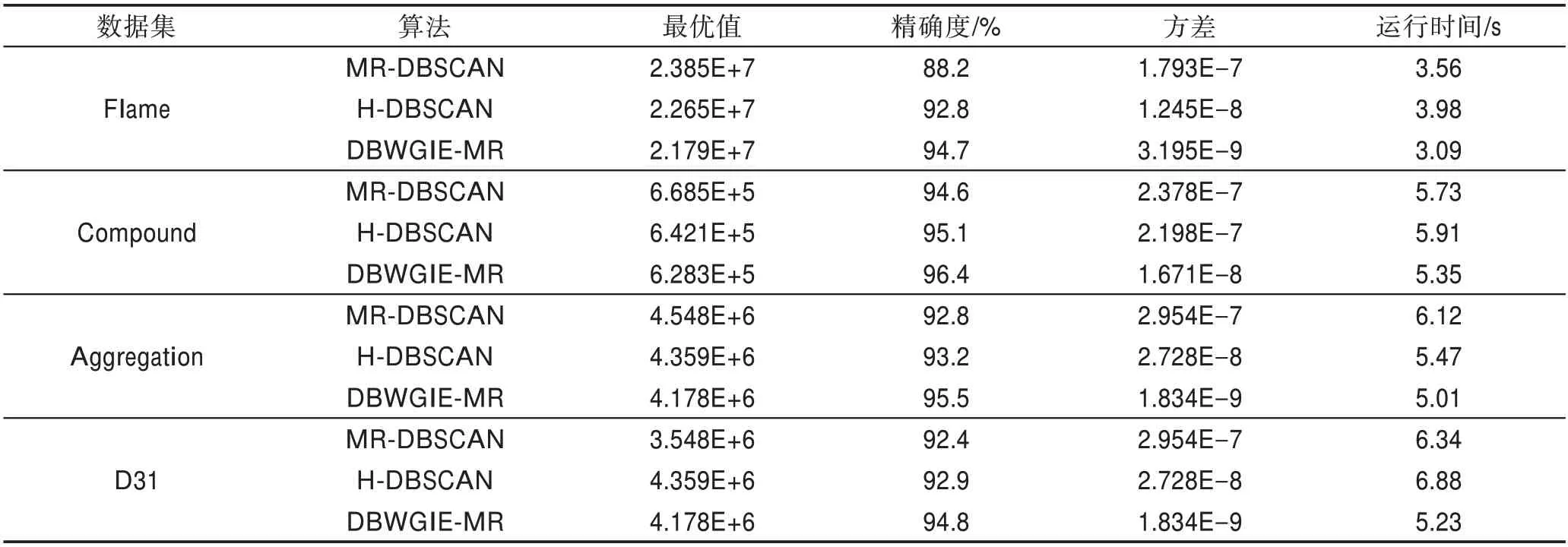
Table 1 Comparison of results in different clustering algorithms表1 各算法的聚類結果比較分析

4.7 算法性能的比較分析

為驗證DBWGIE-MR算法在大數據環境下的運行性能，實驗數據在基于D31數據集下進行實驗，首先將D31數據集中的點數量進行擴充，構造成行數為300萬行（0.6 GB）、500萬行（1 GB）、1 100萬行（2 GB）、1 600萬行（3 GB）的大數據集。同時，為驗證算法在Hadoop并行化框架下的計算能力，采用算法的加速比進行衡量。算法的加速比是指通過并行化計算使得算法的運行時間降低從而得到的性能提升，加速比通常被作為檢驗并行化算法性能的重要指標。在不同數據集規模下，DBWGIE-MR算法的實驗結果如圖7所示。

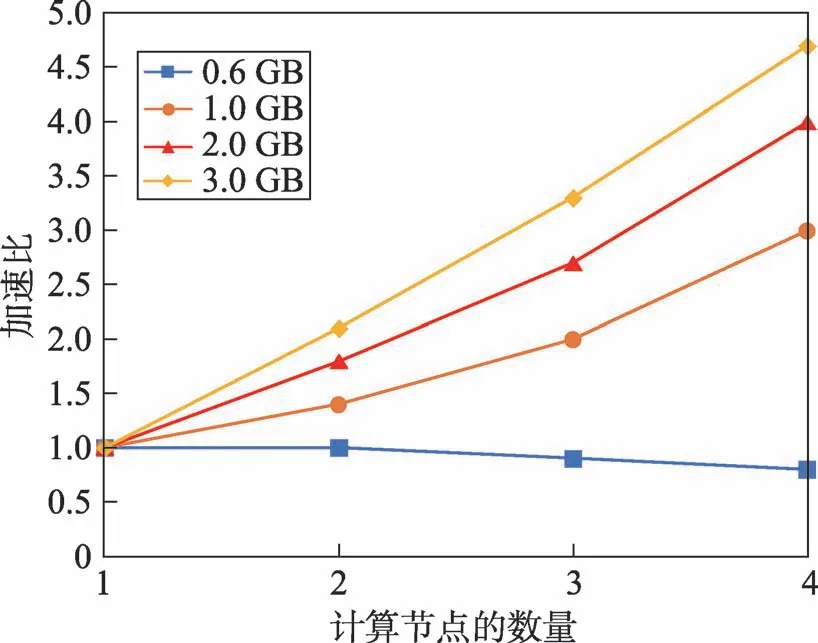
Fig.7 Acceleration rate of algorithm on different computing nodes圖7 算法在不同計算節點下的加速比

從圖7中可以看出，DBWGIE-MR算法在處理大數據集上具有很好的加速比。在一開始數據集較小時，如圖中的0.6 GB數據量所示，隨著計算節點數量的增加，加速比趨近于1.0，甚至在節點4時，出現了下降的趨勢，加速比降低了0.2，這是由于在數據集的規模較小時，數據量遠小于集群所處理的數據量，將數據分散到不同的計算節點中產生了不同的時間開銷，包括集群運行時間、任務調度時間、節點存儲時間等，這些開銷降低了算法的計算速度，因此在這種情況下的并行效果是較低的；而在數據規模達到3.0 GB時，算法在4個節點下計算的加速比為4.6，比在1個節點下計算提高了3.6，原因是隨著數據集規模的逐步增加，算法的能夠并行化計算局部簇和合并局部簇的優點逐漸被放大，使得算法在計算節點增加的同時，加速比呈線性的增長，算法的并行化效果得到很大的提升。這也表明DBWGIE-MR算法適用于處理較大規模的數據集，并且隨著計算節點的增長，并行化的效果更佳。

為進一步驗證DBWGIE-MR算法在大數據下的并行化性能，將DBWGIE-MR算法的運行時間分別與MR-DBSCAN[21]、IP-DBSCAN[24]算法進行比較，所有的算法都是基于擴充后的D31數據集以及相同的并行計算節點。實驗結果如圖8所示。

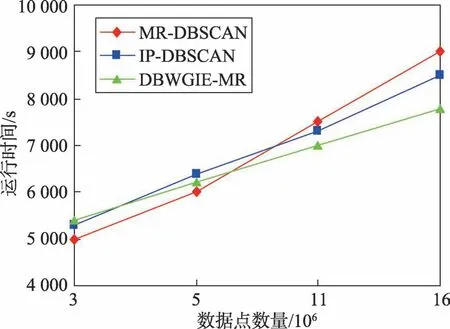
Fig.8 Running time of algorithm in different data sets圖8 算法在不同數據集規模下的運行時間

從圖8中可以看出，在數據集規模較小時，即數據點的數量在3×106左右時，MR-DBSCAN算法完成聚類所需的時間最少，運行時間比IP-DBSCAN算法和DBWGIE-MR算法分別減少102 s和95 s，DBWGIEMR算法執行時間則相對較長，原因是在數據集規模較小的階段，DBWGIE-MR算法需要采用ADG策略和WGIE策略自適應地劃分數據空間以及計算每個網格單元的密度，增加了算法處理數據集的時間。然而，隨著數據集的規模提升，數據集的規模為11×106時，可以明顯看到，IP-DBSCAN算法和DBWGIEMR算法的運行時間分別比MR-DBSCAN算法減少了160 s和400 s，原因在于在大規模數據集下，聚類過程中產生的局部簇的數量明顯增加，而相較于MR-DBSCAN算法，IP-DBSCAN算法采用了并查集對局部簇進行合并，加快了局部簇的收斂，因此在合并局部簇上所需的計算時間有所減少，DBWGIE-MR算法更是在并查集合并局部簇的基礎上，提出并行化合并局部簇，更進一步加快了對局部簇的合并計算，因此DBWGIE-MR算法的運行時間要少于IPDBSCAN算法；當數據規模為16×106時，DBWGIEMR算法的運行時間明顯要少于MR-DBSCAN和IPDBSCAN算法，分別降低了400 s和700 s，這也更加表明了在數據規模較大的情況下，DBWGIE-MR算法能更快地對數據進行處理得到結果，并行化效果更佳。

5 結束語

為解決大數據下基于密度的聚類算法中的數據網格化劃分不合理，提高聚類結果的精確度以及在大規模數據集下的并行化效率，本文提出了基于MapReduce和加權網格信息熵策略的DBWGIE-MR算法。該算法首先根據數據點空間分布狀況，提出ADG策略，自適應劃分網格單元；其次為了提高聚類效果，針對每個數據分區，提出NE策略構建其加權網格用于加強網格之間的關聯性；同時提出WGIE策略來計算網格密度以及密度聚類算法的ε鄰域和核心對象，使密度聚類算法更適用于加權網格；接著結合MapReduce計算模型，提出并行計算局部簇算法COMCORE-MR，從而提升算法的總體并行化效率；最后提出了基于并查集的局部簇合并算法MECORE，用于加快合并局部簇的收斂速度，并結合MapReduce計算模型，提出了并行合并局部簇算法MECORE-MR，實現了并行化地合并局部簇，從而更快地得到聚類結果的全局簇，提升了基于密度的聚類算法對局部簇合并的效率。與其他并行化密度聚類算法相比，該算法能根據數據之間的分布狀況來自適應確定網格劃分邊長，以及構建加權網格來加強網格單元之間的聯系，利用該算法的獨特優勢來實現聚類。實驗在四個標準數據集上進行對比分析，結果表明DBWGIE-MR算法在聚類精度、尋優能力和算法穩定性上都有顯著的提高。此外，在擴充后的大規模數據集的實驗中，也驗證了DBWGIE-MR算法具有較好的并行化效果。結果也表明，相比MR-DBSCAN算法和IP-DBSCAN算法，DBWGIE-MR算法在面對大規模的數據集下的并行化效率更強。雖然改進后算法的聚類精度有所提升，但仍存在提升空間，并且本文并未解決網格單元密度閾值的設置問題，算法并行化性能還有待進一步提高，以上這些將是下一步的研究工作。