基于改進人工勢場法的USV全局路徑規劃*
薛學華 馮 輝* 徐海祥 龔銘凡
(高性能船舶技術教育部重點實驗室1) 武漢 430063) (武漢理工大學交通學院2) 武漢 430063)
0 引 言
水面無人艇(USV)以其無人化水平高、機動性能良好,以及可自主執行任務等優點被廣泛應用于軍民領域.路徑規劃是無人艇自主航行模塊的核心內容,為滿足無人艇在復雜海洋環境下實現自主航行的需求,需要不斷提升無人艇的路徑規劃能力,確保所規劃出的路徑可靠高效.無人艇路徑規劃技術是指給定起始點、目標點,以及障礙物信息,在滿足一定的評價指標的情況下,在出發點到目標點之間通過使用某種路徑規劃方法規劃出一條最優的安全路徑.目前常用的路徑規劃方法有人工勢場法[1]、可視圖法[2]、蟻群算法[3]以及遺傳算法[4]等.人工勢場法是一種虛擬力場法,因其原理簡單,運算時間短,生成的路徑較為平滑被廣泛的應用在無人艇路徑規劃中[5].可視圖法是一種圖搜索算法,其優點是結構簡潔,規劃路徑短,缺點是在環境信息復雜的情況下,運算時間會大大增加[6].
傳統的人工勢場法雖然原理清晰簡單但是仍存在以下幾個不足之處:狹窄航道內抖振的問題、較為容易陷入局部極小值的問題及目標點不可到達的問題.針對以上缺點,許多學者提出不同的改進方法:劉義等[7]針對局部極小值的問題提出修改斥力勢場函數的方法,Saeid等[8]針對目標不能到達的現象提出一種沿墻運動的方法,潘洲等[9]通過設置動態虛假目標點來使機器人離開局部極小值點.
文中針對上述存在的三個不足之處進行詳細分析,分別提出三種改進方法:①通過添加艏向角限制,保證船舶狹窄航道內迅速從抖振狀態恢復至沿航道方向前進;②提出自適應參數調整回溯法,使得船舶在陷入局部極小值時能夠進行回溯并且迅速脫離局部極小值點;③設置人工勢場法—可視圖法切換策略,使算法能夠高效的解決傳統方法某些情況下無法到達目標點的問題.
1 人工勢場法基本原理
人工勢場法最早是由Khatib[10]提出并且將其運用在移動機器人的路徑規劃領域中,其主體思想是由目標點產生引力場,障礙物產生斥力場,機器人在引力及斥力一起作用下不斷向目標點前進.
總勢場由引力勢場和斥力勢場共同疊加組成:
U=Uatt+Urep
(1)
引力勢場函數為
Uatt(X)=0.5kρ2(X,Xg)
(2)
斥力勢場函數為
(3)
式中:X=(x,y)為機器人位置向量;k,m分別為引力參數與斥力參數;X,Xg,X0分別為機器人當前坐標、目標點坐標以及障礙物坐標;ρ(X,X0),ρ(X,Xg)分別為當前位置到障礙物與當前位置到目標點的距離;ρ0為障礙物影響范圍.
通過對勢場函數進行負梯度求解,可以分別求出引力與斥力的表達式.
(4)
Frep(X)=-Urep(X)=
(5)
在USV的路徑規劃過程中,可以通過將障礙物按照船舶尺寸進行膨脹,得到擴展障礙物范圍,然后把船舶視為質點的方法進行路徑規劃,船舶受力見圖1.
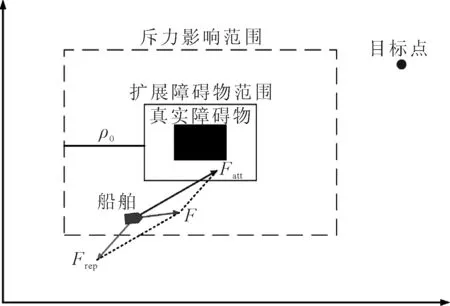
圖1 船舶受力示意圖
合力F將驅動船舶規避障礙物,向目標方向運動.該方法雖然原理簡單,但仍存在下列幾個缺陷.
1) 狹窄航道抖振現象 由于船舶的前進方向完全由引力與斥力的合力決定,當船舶航行至狹窄航道時,合力的方向有可能產生劇烈變化,導致船舶在狹窄航道內出現劇烈抖振的現象.
2) 局部極小值問題 當船舶航行至某一時刻時,若出現船舶的合力為零或者引力與斥力共線,船舶將停止或在局部范圍內徘徊.
3) 目標點不可達現象 由式(4)可知,當船舶逐步靠近目標點時,引力會逐漸變小;由式(5)可知,當船舶逐漸接近障礙物的時候,斥力將逐漸增大.因此,當目標點周圍存在障礙物時,隨著船舶接近目標點,將會出現船舶在目標點周圍的局部范圍內往復運動的狀況,從而導致規劃失敗.
2 改進人工勢場法
2.1 解決狹窄航道抖振問題
使用傳統人工勢場法進行路徑規劃時,在船舶運行至狹窄航道時,會出現不必要的往復抖振現象.主要原因為船舶在狹窄航道時,其主要受力來自目標點的引力以及來自岸壁兩邊的斥力,當船舶靠近一側岸壁時,近端岸壁將產生較大斥力將其向遠端岸壁排斥,由于航道狹窄,導致船舶在接下來的較小周期內運行到另一個岸壁附近,使得另一岸壁同樣產生較大斥力,如此往復,就會導致船舶出現抖振現場,船舶將耗費大量時間才能駛離狹窄航道甚至出現停滯不前的現象,見圖2.

圖2 人工勢場法狹窄航道抖振示意圖
針對傳統人工勢場法出現的抖振現象,分析其主要原因是船舶在接近一側岸壁時受到斥力作用,以較大角度向反方向運動,使得船舶主要是在垂直岸壁方向運動,而沿著岸壁方向的運動非常少.
為了限制船舶在狹窄航道中垂直岸壁方向的運動,同時使規劃出的路徑能滿足船舶行駛時的實際應用,本文將船舶最大艏向角限制加入到路徑規劃中,對規劃中船舶的方向變化加以限制,從而抑制船舶在接近岸壁一側的大角度反向運動,達到消除抖振的效果.艏向角限制示意圖見圖3,其中最大轉向角θ=60°,黑色路徑點為未添加艏向角時船舶可能出現的大角度反向運動,加粗路徑點為添加艏向角限制后,船舶通過設置最大轉向角約束避免大角度反向運動現象的產生.
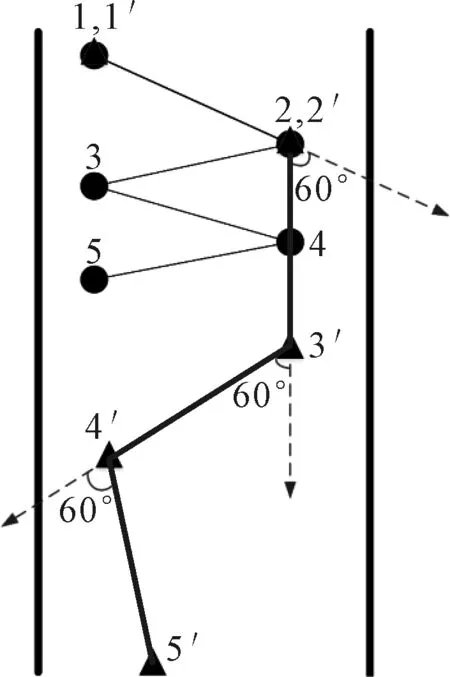
圖3 狹窄航道添加艏向角限制示意圖
2.2 解決局部極小值問題
局部極小值問題是指船舶在移動過程中的某個時刻,在當前位置下目船舶受到的引力與斥力大小相等,方向相反,導致當前位置點船舶合力為0,船舶不再移動或者在小范圍內往復抖動的現象.典型的局部極小值問題可以細分為兩種情況,見圖4.
1) 在船舶與目標點之間存在單一障礙物,且船舶、障礙物和目標點處于同一直線.此時,隨著船舶逐步向目標點運動,斥力逐漸增大,引力逐漸減小,最終運動到某個斥力與引力大小相近的位置,船舶在該處停止或者在該點處往復抖動導致船舶無法到達目標點.
2) 在復雜障礙物情況下,多個障礙物組成的復雜障礙物環境所產生的總斥力與目標點產生的引力合力為0,導致船舶無法到達目標點,其中最典型的復雜障礙物情況為C形障礙物.

圖4 局部極小值問題
對于傳統方法出現的局部極小點問題,將情況一與情況二進行分別處理.
針對情況一,其主要原因是船舶、障礙物和目標點三者共線,船舶受的合力平行于該直線,船舶只能沿著該直線運動,導致無法繞過障礙物,只能在障礙物前來回往復運動,該情況同上述狹窄航道抖振問題相似,通過加入艏向角限制,使船舶無法進行大角度折返運動,限制船舶下一點位移,使其離開局部受力平衡狀態,從而解決情況一的局部極小點問題.
針對情況二,提出自適應參數調整回溯法對傳統方法進行改進.主要步驟見圖5.
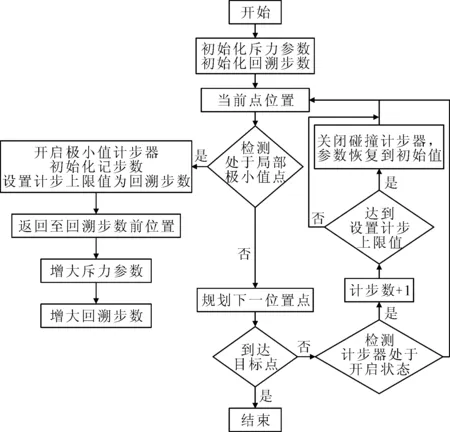
圖5 自適應參數調整回溯算法流程圖
其中,局部極小值狀態判別為
ρ(XJ,XJ-b) (6) 式中:ρ(XJ,XJ-b)為在第J個周期船舶的位置與在第J-b個周期船舶的位置之間的距離;k為極小值判斷系數;l為步長. 斥力參數更新公式為 m=tm (7) 式中:t為斥力更新參數. 回溯步長更新公式為 b=b+w (8) 式中:w為回溯步長更新參數. 算法演示見圖6. 圖6 自適應參數調整回溯算法示意圖 通過上述回溯算法,船舶能回溯到若干步長前的位置,在增大斥力參數的情況下,船舶有足夠大的力逃離極小值點.若船舶在連續幾個周期內,持續處于極小值狀態,斥力參數將持續變大,并且隨著回溯步數的增加,船舶能夠在較短周期內迅速擺脫碰撞狀態和逃離局部極小值點;通過設置相應計步器以及計步上限值,船舶能在激活回溯后的連續若干個周期處于正常狀態后將斥力參數恢復至初始狀態,保證算法在安全狀態下的以正常的參數運行. 當目標點周圍存在障礙物時,隨著船舶向目標點逐步接近,船舶受到的引力減小,斥力增加,將會出現船舶所受斥力大于其所受引力的現象,從而船舶無法到達目標點. 針對目標點不可達問題,本文采用切換可視圖法來進行改進.可視圖法(V-Graphicic),先構造可視圖G(V,E),點集V=V0∪{S,G},V0為各個障礙物的所有端點,S為出發點,G為目標點,E為可見邊的集合[11].要求V中任意兩點之間連線都不能同所有障礙物存在相交的現象.通過對邊賦權值,即可通過搜素算法找出一條從起點到終點的最優路徑.可視圖法優點是結構簡單,不足之處在于隨著環境的復雜度上升,其運算時間將會大大加長. 文中提出將人工勢場法與可視圖法進行結合,具體表示為將船舶的路徑規劃分為兩個階段,第一階段采用人工勢場法進行規劃,當運行至某個周期時,船舶行駛至包含目標點的障礙物的斥力影響范圍內,激活切換,將人工勢場法算法切換至可視圖法,完成剩余階段的路徑規劃.該切換策略將整體的環境信息進行劃分,為可視圖法提供了僅包含第二階段的小范圍的點集環境.通過設置該人工勢場法-可視圖法切換策略,不僅能夠融合人工勢場法的實時性好與可視圖法的結構簡單的優點,還能克服人工勢場法目標點不可達以及在復雜環境下可視圖法運算時間過長的缺點. 人工勢場法在繞開障礙物的時可能會出現過大幅度的避讓現象或者在復雜障礙物環境下會出現局部打轉等現象導致生成一些不必要的路徑點,使生成的路徑不是最優.由文獻[12]提出的改進方法,設置路徑點刪減算子,當第i個點pathpointi與第i+2個點pathpointi+2二者相連的線段不會與任意障礙物相交的情況下,刪除第i+1個點pathpointi+1,見圖7.通過增加路徑點刪減算子,可以去除人工勢場法運行過程中產生的多余路徑點,降低規劃出的路徑總長度. 圖7 路徑點刪減算子示意圖 傳統方法與改進方法在狹窄航道中的仿真對比結果見圖8,其中起始點坐標為(64,0),目標點坐標為(126,160),引力參數k=1,斥力參數m=100,障礙物擴展參數ρe=5,步長l=5,斥力影響范圍ρ0=50,最大轉向角θ=60°. 圖8 狹窄航道情況下仿真比較 由圖8可知,傳統方法在狹窄航道情況下會出現明顯的抖振現象.利用本文提出的增加艏向角限制的改進方法在狹窄航道情況下表現良好,船舶在進入狹窄航道后,不會出現大角度折回現象,從而使船舶能迅速沿岸壁方向穩定前行,有效抑制了抖振現象的產生. 針對情況一下的局部極小值問題分別對傳統方法以及改進方法進行仿真比較.結果見圖9,其中起始點坐標位置為(0,80),目標點坐標位置為(100,80),引力參數k=1,斥力參數m=200,障礙物擴展參數ρe=5,步長l=5,斥力影響范圍ρ0=30,最大轉向角θ=60°. 圖9 情況一仿真比較 由仿真結果可知,傳統方法在船舶運行到第七個步長時陷入局部最小點,無法繼續向目標點移動,最后導致路徑規劃不成功.增加了艏向角限制之后,當船舶運動至局部極小點位置時能以相應限制角度轉向,向目標點繼續運動,最終成功到達目標點. 針對情況二下的局部極小點問題分別對傳統方法以及方法進行仿真比較,仿真結果見圖10,其中起始點坐標位置為(0,300),目標點坐標位置為(300,0),引力參數k=1,斥力參數m=500,障礙物擴展參數ρe=5,步長l=5,斥力影響范圍ρ0=70,最大轉向角θ=60°,回溯步數b=10. 圖10 情況二仿真比較 由仿真結果可知,傳統方法在進入U形區域中陷入局部極小點.通過增加本文提出的自適應斥力參數回溯法,在經過5次回溯后,船舶能繞過U型障礙物,最終順利到達目標點. 針對目標點不可達問題分別對傳統方法以及改進方法進行仿真比較,仿真結果見圖11.其中起始點坐標為(0, 0),目標點坐標為(150,150),引力參數k=1,斥力參數m=200,障礙物擴展參數ρe=5,步長l=5,斥力影響范圍ρ0=30. 圖11 目標點不可達問題仿真比較 由圖11可知,在目標點周圍有障礙物存在的情況下,傳統方法規劃出的路徑無法到達目標點,通過采用人工勢場法-可視圖法結合算法,船舶運行至包含目標點的障礙物斥力范圍內時,切換成可視圖法,完成剩余階段的路徑規劃,順利到達目標點. 選取算法的初始參數為:起始點坐標位置為(0,1 000),目標點坐標位置為(850,100)引力系數k=1,斥力參數m=500,步長l=5,最大轉向角θ=60°,障礙物擴展參數ρe=5,斥力影響范圍ρ0=70,回溯步數b=5,極小值判定系數k=0.5,斥力系數更新參數t=5,回溯步數更新參數w=5,分別采用傳統方法、可視圖法以及改進方法進行仿真,見圖12和表1. 圖12 復雜地圖環境中的傳統方法、可視圖法和改進方法 表1 算法比較 由圖12和表1可知,傳統方法在復雜環境中陷入局部極小值導致無法完成剩余路徑規劃,改進方法與可視圖法都能規劃成功,在規劃的路徑長度相差不多的情況下,改進方法耗時比可視圖法縮減了10倍. 本文對傳統人工勢場法存在的狹窄航道抖振問題、局部極小值問題以及目標點不可達問題進行詳細分析,針對狹窄航道出現的大角度反向運動,提出設置艏向角限制,有效的抑制了抖振現場的產生;通過設置艏向角限制以及采用自適應參數調整回溯法分別解決了由斥力與引力共線以及由復雜障礙物產生的極小值問題,通過設置人工勢場法—可視圖法切換策略,在保證算法良好實時性的情況下解決了目標點不可達問題.最后對所提出的各改進方法在Matlab上仿真,結果證明了改進算法的可行性.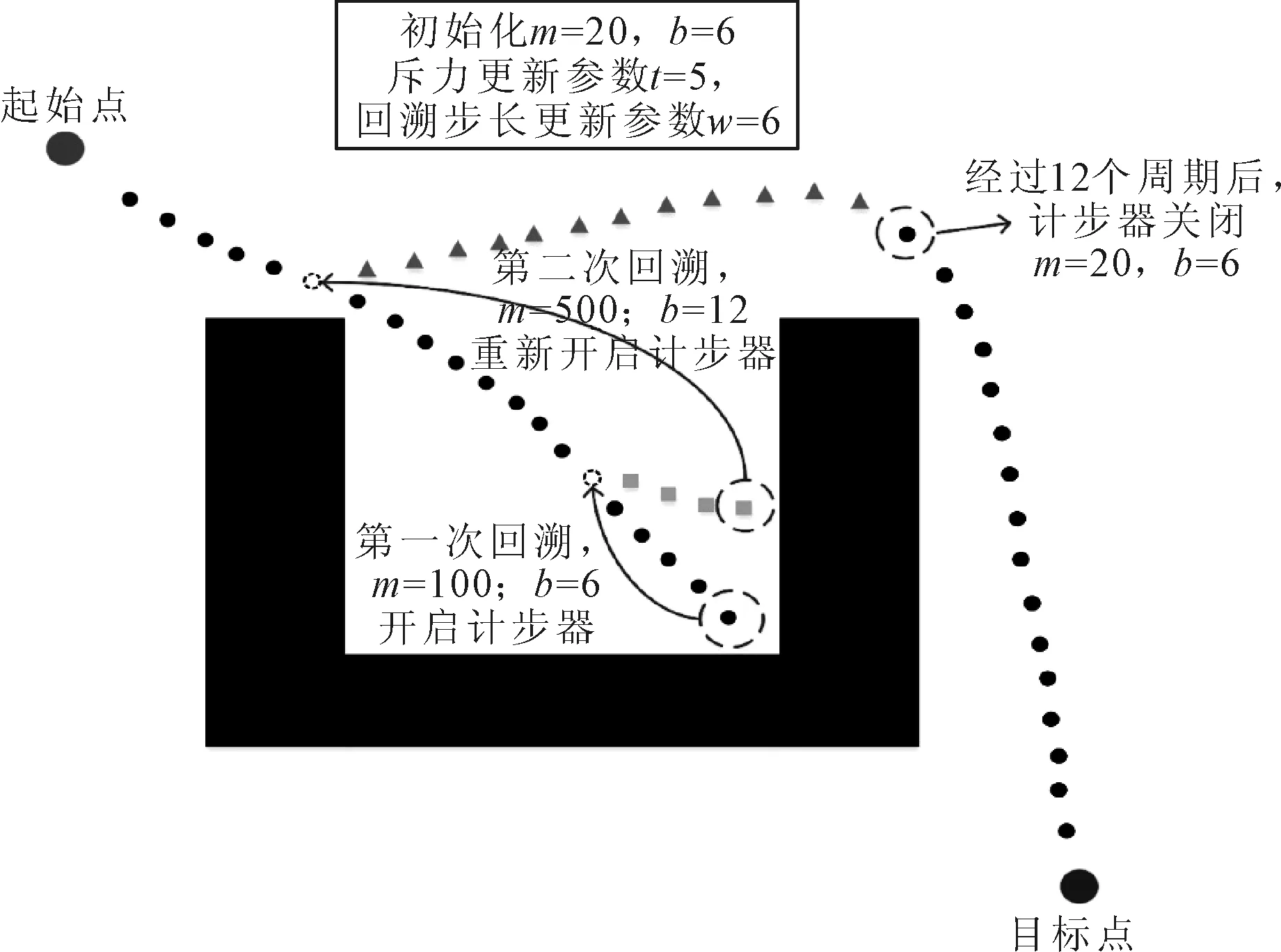
2.3 解決目標點不可達問題
2.4 路徑點刪減算子

3 仿真及結果分析
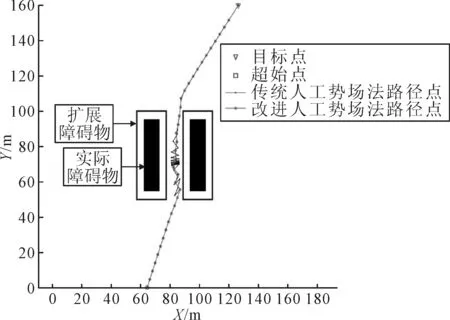
3.1 狹窄航道抖振現象仿真分析
3.2 局部極小值現象仿真分析


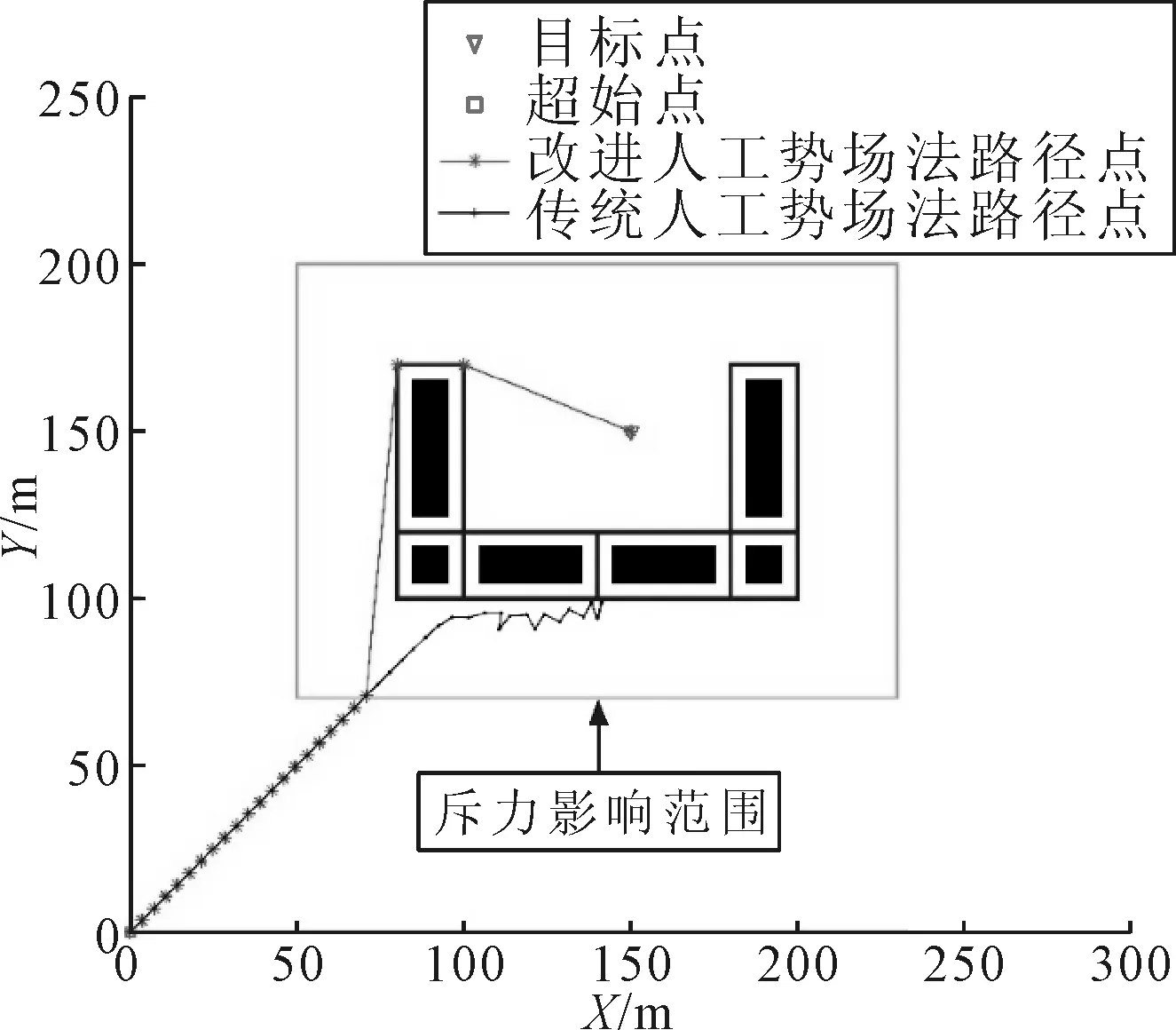
3.3 目標點不可達問題仿真分析
3.4 復雜地圖環境仿真分析


4 結 束 語

