基于IFOA-GRNN 的電力系統短期負荷預測

張兆旭，劉成忠

（1. 甘肅農業大學 機電工程學院，甘肅 蘭州 730070；2. 甘肅農業大學 信息科學技術學院，甘肅 蘭州 730070）

電力系統負荷預測是指考慮系統運行的某些特性、擴能決策、自然與社會影響等諸多因素，在滿足一定準確度的要求下，確定未來某一特定時刻的負荷數據。其核心是預測模型或技術問題。傳統模型一般是由數學表達式來構造，具有簡單、快速等優點，但也存在較多的局限性，如魯棒性較差、無自適應能力等。近年來，應用神經網絡進行負荷預測頗受研究人員關注，其不僅繼承了傳統模型的特點，還考慮了影響負荷的一些其他因素［1］。

1 廣義回歸神經網絡概述［2］

廣義回歸神經網絡（generalized regression neural network，GRNN）是以數理統計為基礎的一種徑向基函數神經網絡（RBFNN）。它不需要事先確定方程的形式，而是使用概率密度函數，所以具有很強的非線性映射能力。此外，即使只有少量樣本，網絡的輸出也能收斂到最優值，適合解決有關非線性問題。

GRNN 的最大特點是：當樣本確定后，其結構與權值就確定，對網絡的訓練實際上是尋找光滑參數（spread）的過程。如果光滑參數不合適，那么GRNN 就無法達到最佳的優化效果。為了讓預測結果最接近真實值，必須找到一個最佳光滑參數。

2 果蠅優化算法及其改進方法

2.1 果蠅優化算法的基本原理［3］

果蠅優化算法（fruit fly optimization algorithm，FOA）是以果蠅尋找食物的行為為基礎而衍生出的一種全局尋優的群體智能算法。果蠅的嗅覺和視覺器官十分強大，可以聞到40 km 以外的食物，然后通過靈敏的視覺發現食物與同伴的聚集位置，并飛往該方向。

依據以上介紹，可將FOA 歸納為7 個步驟：

（1）預先規定果蠅的群體規模P、總迭代數T，隨機給出果蠅的群體位置X、Y。

（2）給出果蠅個體通過嗅覺搜索食物的隨機方向和距離，R為搜索距離。

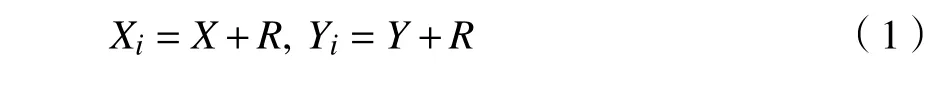
（3）由于食物位置無法事先知道，所以預估與原點的位移Di，再計算氣味濃度判定值Si，即Di的倒數。

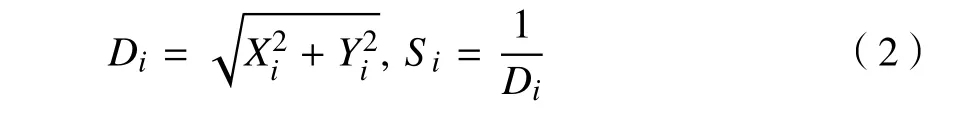
（4）將氣味濃度判定值Si轉換成氣味濃度判定函數（即適應度函數F），計算個體位置的氣味濃度SL, i。

（5）找出群體中氣味濃度最低的個體（求極小值），對應的最佳氣味濃度為BS，對應位置為BI。

（6）對最佳氣味濃度及其X、Y坐標（位置BI）進行保存，此時群體通過視覺飛往該位置。

（7）進入迭代優化過程，即重復步驟（2）～（5），同時判斷最佳氣味濃度是否比前一次迭代更優。若是則執行步驟（6），否則轉為步驟（2），直到滿足總迭代數時結束。

2.2 果蠅優化算法的改進方法

FOA 不僅簡單，較易理解，而且參數調整少，但和其他群體智能算法一樣，易陷入局部最優，導致收斂速度較慢，收斂精度和穩定性變低［4］。本文針對上述缺點，提出了一種改進果蠅優化算法（improvement of fruit fly optimization algorithm，IFOA），即：在FOA 從進入開始迭代到迭代至一半的過程中，將R增大，這樣既實現了種群多樣性，又保證了果蠅盡可能地跳出局部極值；在FOA 從開始迭代至一半到迭代結束的過程中，將R減小，以提高收斂精度和速度。通過以上兩個過程可提高算法的性能，利用式（5）改進步驟（2），即

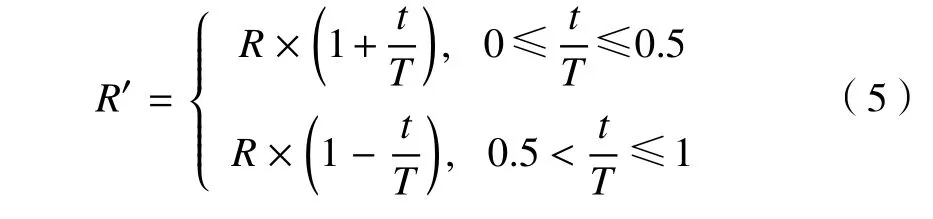
式中：R′改進后的搜索距離；t為當前迭代數。

3 改進果蠅優化算法優化廣義回歸神經網絡（IFOA-GRNN）的計算步驟

果蠅優化算法優化廣義回歸神經網絡（FOAGRNN）的思想，是通過FOA 確定GRNN 的光滑參數最優解，將其預測值與實際值的均方根誤差（RMSE）降到最低，記錄此時的氣味濃度，此值即為光滑參數最優解［5-6］。

本文使用2.2 中的改進方法對FOA 進行改進，從而優化GRNN 的光滑參數。其基本步驟為：

（1）給出初始群體規模P、總迭代數M和果蠅群體位置X、Y。

（2）給出果蠅個體通過嗅覺搜尋食物的隨機方向與距離Xi、Yi。

（3）計算個體與原點的位移Di，再計算氣味濃度判定值Si，即光滑參數。若光滑參數小于0.001，則令其值為1。

（4）將光滑參數代入GRNN 的網絡函數中進行訓練和仿真。將預測的RMSE 作為氣味濃度判定函數，找出個體的味道濃度S'L, i，如式（6）所示。

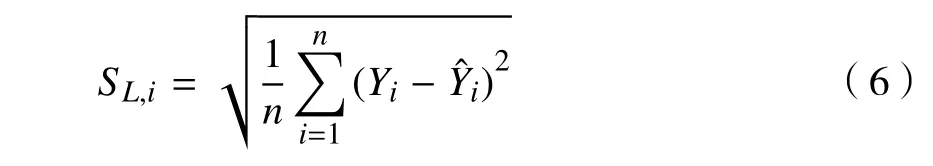
式中：Yi為第i個實際值；為第i個預測值；n為樣本個數。

（5）找出群體中氣味濃度最低的個體，即為RMSE 最小值。

（6）對最佳光滑參數與個體坐標進行保存，此時群體通過視覺飛往該位置。

（7）迭代優化，重復步驟（2）～（5），若RMSE 優于前一次迭代，則執行步驟（6）。

（8）判斷迭代數是否滿足，若滿足則得到最佳光滑參數，并代入GRNN 模型仿真。

4 電力系統短期負荷預測模型的建立

4.1 預測地區負荷的分析

圖1 為預測地區某晴天工作日和晴天休息日的24 h 負荷曲線。從圖中可知，工作日和休息日的負荷差距較大。一般情況下，工作日的負荷高于休息日的負荷。這是因為用于工業生產的負荷較多地出現在工作日，而并非休息日。

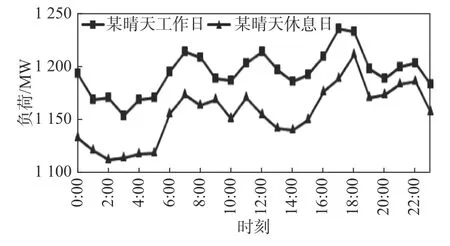
圖 1 某工作日和休息日的負荷曲線Fig. 1 Load curve for a working day and a rest day

圖2 為預測地區某晴天（平均溫度25.6 ℃）和雨天（平均溫度17.1 ℃）的24 h 負荷曲線。從圖中可以看出，晴天的負荷一般高于雨天。這是因為晴天的溫度較高，空調等耗電量較大的設備使用率較高。

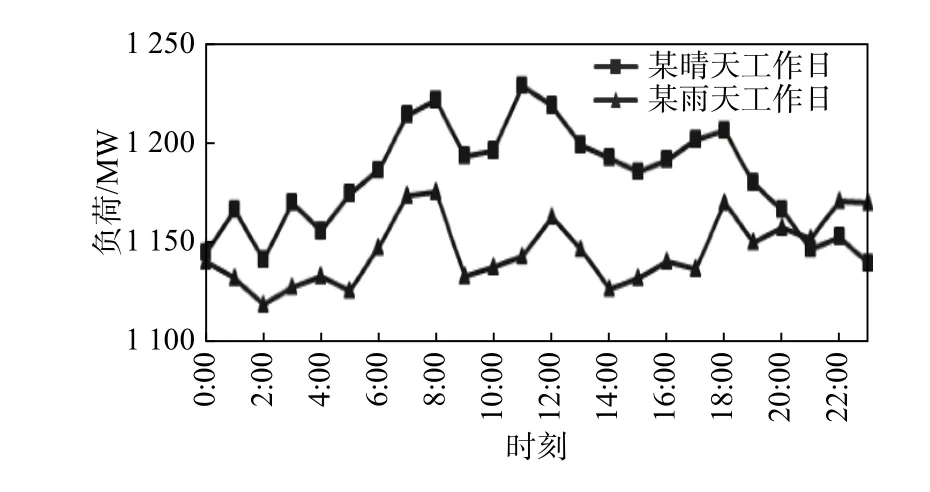
圖 2 某晴天和雨天的負荷曲線Fig. 2 Load curve of a sunny day and a rainy day

綜合分析預測地區的負荷數據發現，一天中負荷的變化具有規律性，峰值一般集中出現在6:00～8:00、10:00～12:00、16:00～18:00，而谷值一般出現在2:00～4:00、8:00～10:00、13:00～15:00、19:00～21:00。此外，無論是工作日或休息日，晴天或陰雨天，相鄰時刻的負荷一般差距不大。換句話說，電力負荷一般都是連續變化的，較少出現突變。

4.2 數據歸一化

（1）負荷和溫度數據

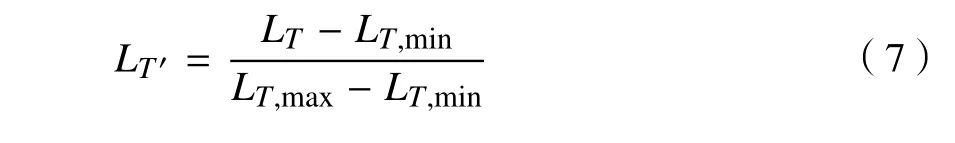
式中：LT'為歸一化后的值；LT為輸入值；LT,max為最大值；LT,min為最小值［7］。

在神經網絡的輸出中，利用式（8）進行反歸一化，換算回輸入值，即

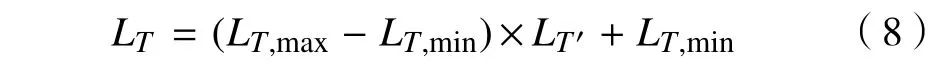
（2）氣象特征和日期類型

氣象特征和日期類型是非量值，無法直接作為神經網絡的輸入量，故對氣象特征進行量化處理。日期類型量化為：工作日取為1；休息日取為0。氣象特征歸一化值如表1 所示［8］。

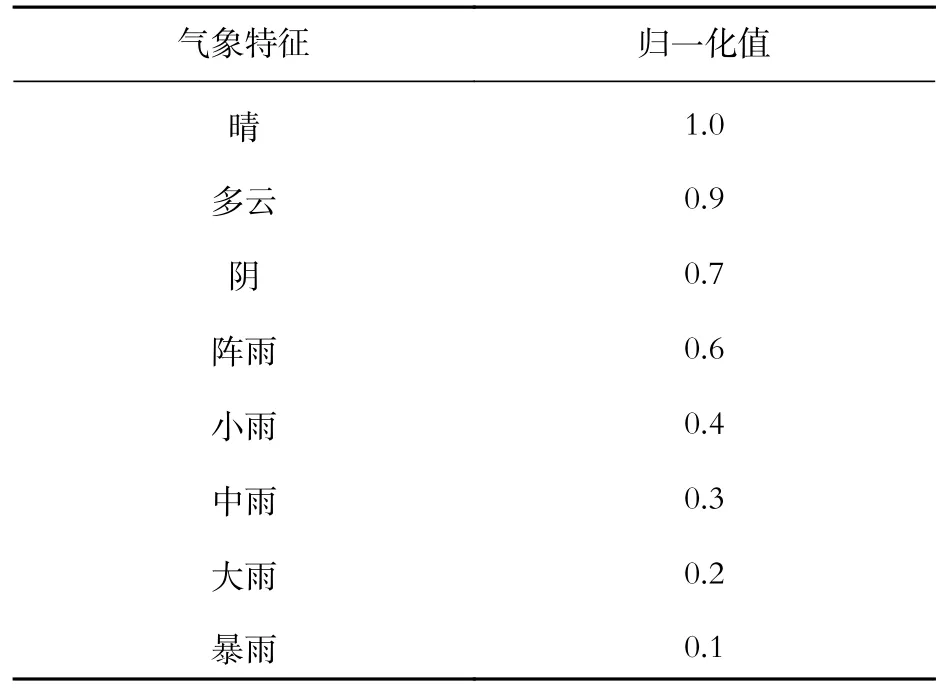
表 1 氣象特征歸一化值Tab. 1 Normalization of the meteorological features

4.3 建立預測模型

神經網絡預測模型有2 種構造方法，分別為：① 多輸入多輸出：以未來某天24 個時刻的負荷為輸出，一次性用一個神經網絡預測；② 多輸入單輸出：以未來某天某時刻的負荷為輸出，建立24 個神經網絡預測［9］。

本文采用第2 種方法，即利用多輸入單輸出模型進行GRNN 的建模和預測。設定樣本輸入變量為27 維，其構造方法如表2 所示；樣本輸出變量為1 維，即預測某一時刻負荷。

表 2 樣本輸入變量的建模Tab. 2 Modeling of the sample input variables

5 預測誤差計算及分析

本文選取甘肅省某地區某年7 月16 日～8月27 日的負荷數據和相關資料作為訓練樣本，分別通過誤差反向傳播神經網絡（BPNN）、FOAGRNN 以及IFOA-GRNN 預測8 月28 日全天24個整點時刻的負荷，然后和實際負荷值進行誤差比較。

在BPNN 中，隱含層節點數為53，隱含層節點轉移函數選tansig，輸出層節點轉移函數選logsig，訓練次數為1 000 次，學習速率為0.5，訓練目標為0.000 1［10］。在FOA-GRNN 和IFOAGRNN 中，最大迭代數為100，種群規模為20。

3 種方法的預測相對誤差如表3 所示，其負荷預測值與實測值如圖3 所示。

對短期負荷進行預測時要求相對誤差一般不超過3%［1］。由表3 中可知，BPNN 的預測相對誤差非常不穩定，雖然其平均相對誤差為2.16%，但有5 個時刻的預測相對誤差卻遠大于3%，且由圖3（a）中可看出，其預測值與實測值相差較大。

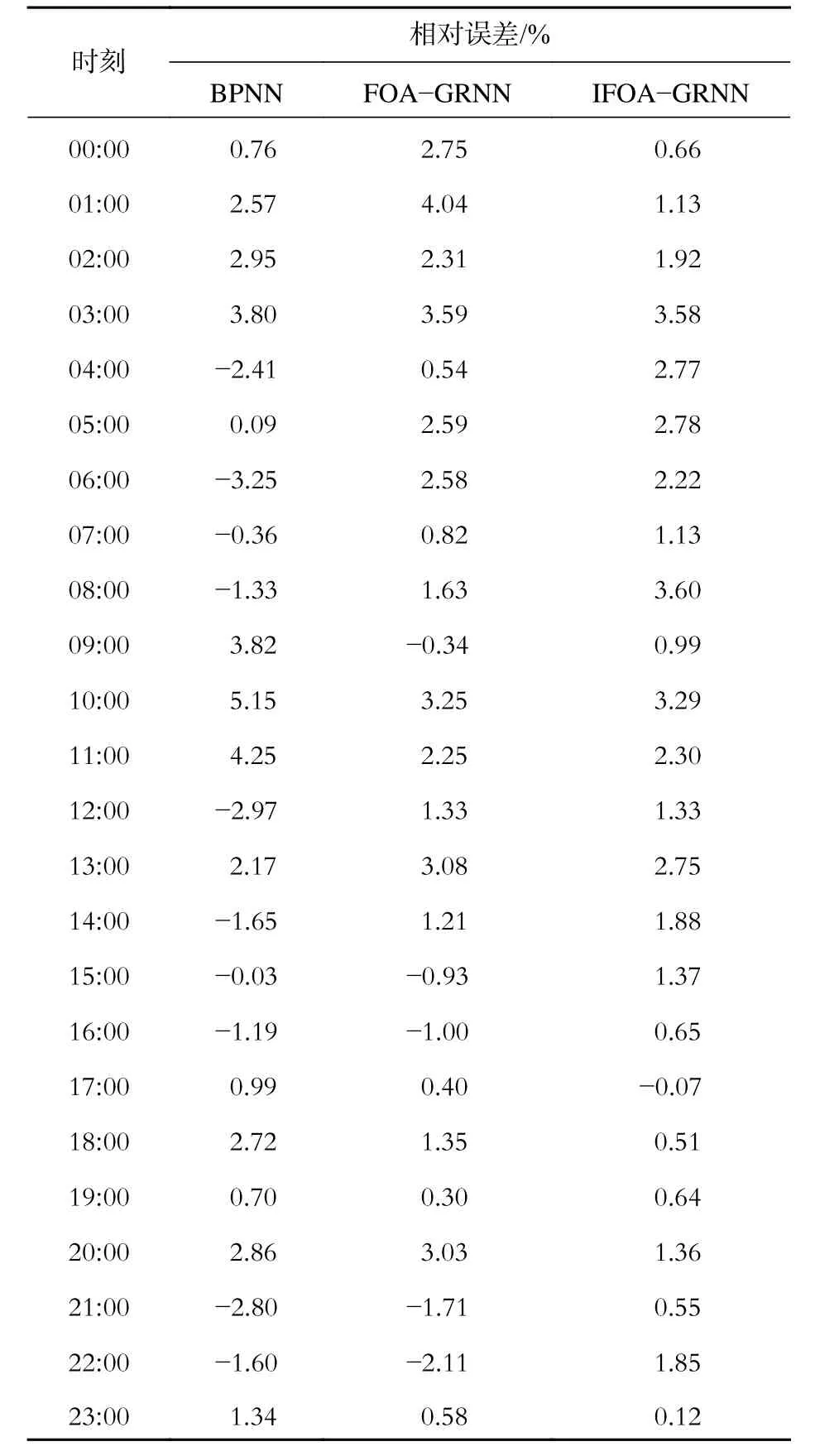
表 3 3 種方法的預測相對誤差Tab. 3 Relative prediction errors of the three methods

利用FOA-GRNN 和IFOA-GRNN 進行預測時，相對誤差超過3%的時刻分別有5 個和3個。由圖3（b）、（c）中可知，這兩種方法整體上都能反映負荷變化的趨勢，平均相對誤差分別為1.82%和1.64%。綜合考慮發現，IFOA-GRNN的預測性能優于FOA-GRNN 和BPNN。

6 結 論

由于電力系統負荷的預測對象是不定事件，因此，短期負荷預測必須結合預測地區的負荷特點，并考慮多方面的影響因素，選擇合理的預測模型和方法［1］。本文通過對FOA 進行改進，再利用其訓練GRNN 的負荷模型，進而用于甘肅省某地區的短期負荷預測。該模型預測值與實測值比較接近，誤差也較小，表明該方法是一種較為有效的預測短期負荷的方法，可滿足預測的精度要求。