變截面變曲率梁振型的有限元超收斂拼片恢復解和網格自適應分析

王永亮

(1.中國礦業大學(北京)力學與建筑工程學院，北京100083；2.中國礦業大學(北京)煤炭資源與安全開采國家重點實驗室，北京100083)

梁構件在實際工程中廣泛應用，如結構工程中的曲線梁橋[1]、航空航天工程中的機翼翼梁[2]、采礦工程中的礦柱Euler–Bernoulli梁模型[3]等。梁的自由振動是強迫振動研究的基礎，自振頻率可為避免結構共振提供依據[4]，利用振型疊加可分析地震載荷作用下結構的變形量[5]。此外，利用自振頻率和振型可以進行含損傷結構的損傷識別[6?7]，損傷個數、位置和程度的準確識別依賴于高精度的頻率和振型解答[8?9]。本文針對典型的平面變截面變曲率梁構件自由頻率和振型求解開展研究，該類曲梁的軸線在同一平面內、且曲梁的任意位置橫截面均關于上述平面對稱。這類曲梁在面內振動和面外振動相互解耦，需要分別求解[10]，如何精確、有效地求解變截面變曲率梁的連續階頻率和振型成為需求，也是本文的研究目標。

有限元法是求解曲梁自由振動頻率和振型近似解的重要方法，被應用于分析不同橫截面[11]、支撐類型[12]、曲線線型形式[13]等復雜梁構件的自由振動問題。以控制和提高有限元解的精度為目標，自適應有限元法被應用于Euler-Bernoulli梁構件[6]、梁系結構[14?15]的頻率和振型的求解，各類新型網格自適應算法[16? 17]為提供滿足預設誤差限的高精度解答提供了高性能計算方案。本文將建立變截面變曲率梁面內和面外自由振動振型的有限元超收斂拼片恢復解的計算方法，并基于振型超收斂解構建網格自適應分析策略，可獲得優化的網格和滿足預設誤差限的連續階頻率和振型。數值算例檢驗了本文方法分析不同曲線形態、多類邊界條件、變曲率、變化截面形式的曲梁面內和面外自由振動連續階頻率和振型的求解效力，表明本文方法分析結果的精確性和有效性。

1 曲梁面內和面外自由振動

考慮圖1所示的平面變截面變曲率梁，曲梁的中性軸坐標為s，坐標系為xy z，其中x、y為曲梁平面內坐標，x沿軸線切向，y沿軸線法向，z垂直于軸線所在平面。面內振動的位移為：沿x軸位移振幅u、沿y軸位移振幅v和繞z軸的轉角振幅ψz；面外振動的位移為：沿z軸位移振幅w、繞y軸的轉角振幅 ψy和繞x軸的扭轉角振幅φx。記曲梁曲率半徑為R(s)，截面剪切剛度修正系數為κ，截面面積為A(s)，對y軸慣性矩為Iy(s)，對z軸慣性矩為I z(s)，極慣性矩為Ip(s)，扭轉常數為J(s)，長度為l。記材料彈性模量為E，剪切模量為G，泊松比為ν，密度為 ρ。

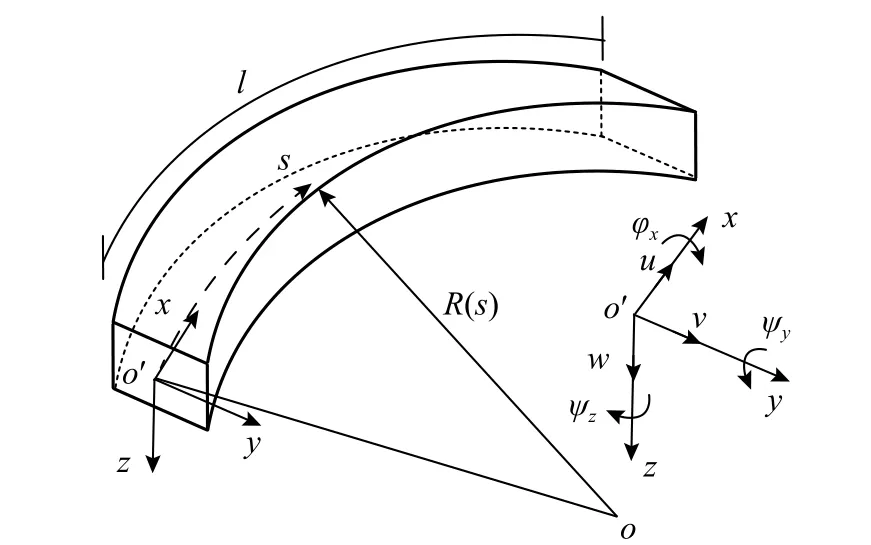
圖1 平面變截面變曲率梁坐標系和符號Fig.1 Coordinatesystemsand symbols of planar nonuniform and variablecurvature curved beam

本文研究的平面曲梁面內自由振動的微分控制方程[18]為：

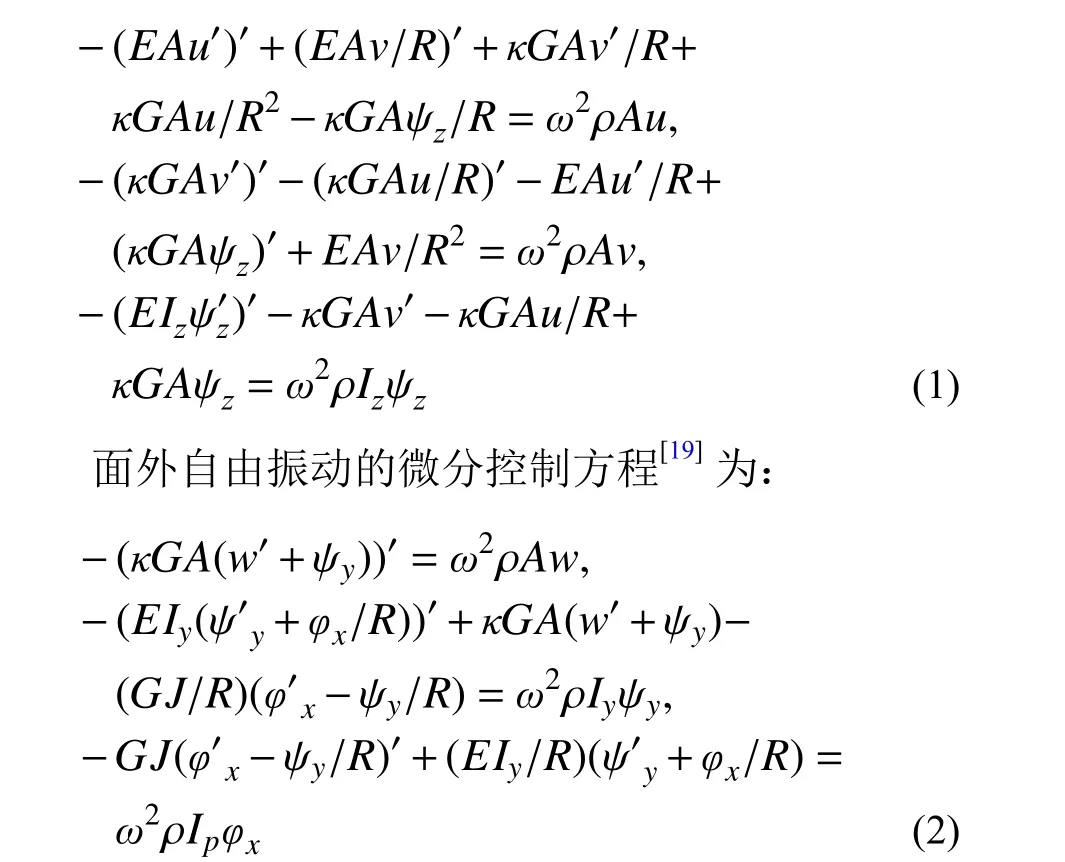
式中：()′=d()/ds；ω為自振頻率。

面內、面外自由振動控制方程式(1)、式(2)均可記為如下矩陣形式的特征值方程：

式中：u為對應的振型(位移)函數向量(面內、面外振動分別為{u,v,ψz}T、{w,ψy,φx}T)，ω、u分別對應于特征值、特征向量，本文亦將(ω,u)合稱為特征對；L、R是相應的微分算子矩陣。

2 振型有限元解

對于求解特征值方程式(3)，在給定有限元網格π下，常規有限元建立如下線性矩陣特征值方程：

式中：D為振型向量的有限元解；K和M是靜力剛度矩陣和一致質量矩陣。采用逆冪迭代法[20]求解，即得當前網格下有限元解(ωh,u h)。

3 振型超收斂拼片恢復解

位移型有限元法以節點位移為基本未知量，有限元位移解在單元內部具有hm+1階(m為當前形函數階次)的超收斂性，在單元節點上具有h2m階的超收斂性，這些節點成為位移超收斂點。超收斂點上解答的誤差比其他區域解答更小，具有更快的收斂速度[20]。利用相鄰單元拼片，并將這些單元節點位移值進行次高階形函數(高于當前形函數階次m，即≥m+1)插值，即可獲得單元域內位移場的超收斂解，形成有限元后處理超收斂拼片恢復方法[6,21?22]。在當前網格下，位移超收斂解比常規有限元解具有更高收斂階。本文對于曲梁的面內和面外自由振動問題，求得當前網格下振型(位移)的有限元解后，利用有限元后處理超收斂拼片恢復方法，將單元e的相鄰單元進行拼片，并進行高階形函數插值處理，可以得到振型的超收斂解：

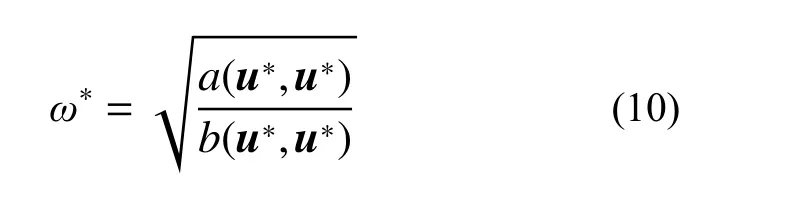
式中，a( )、b( )為應變能、動能內積。

運用Rayleigh 商計算得到的頻率超收斂解比振型超收斂解具有更高的收斂階[23]，因此，本文針對振型進行誤差估計和控制，即可獲得高精度的振型解，并確保頻率解的準確性。

4 誤差估計和網格細分加密

利用振型誤差估計，網格可以進行優化處理來降低和控制振型的誤差，達到預設的解答精度。本文方法采用式(14)對每個有限元單元e上的振型誤差進行判斷，如果誤差控制式(14)不滿足，則表明該單元上振型解答的誤差過大，需要通過進行網格優化處理，本文采用單元均勻細分加密的方式來增加模型自由度、降低單元上解答的誤差[6,24]。當前單元細分生成的新單元長度與目前誤差和單元階次相關，即利用當前誤差可以估計新單元長度：

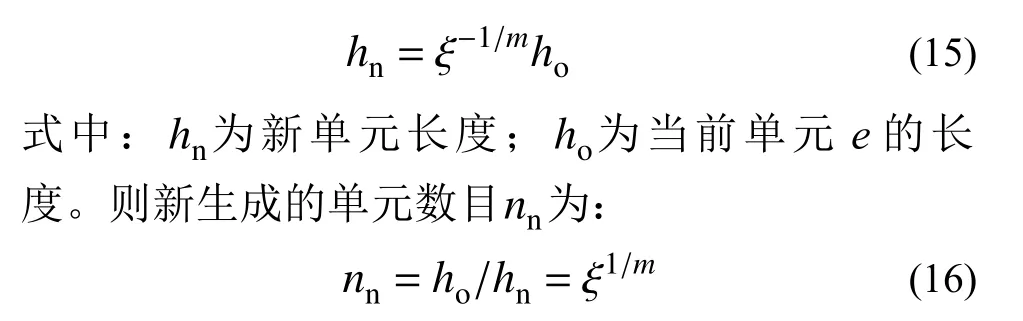
為適應問題的復雜性，往往在求解域上使用非均勻分布網格才能高效地獲得可靠解答。上述自適應分析過程將單元均勻細分加密，如果每次細分出過多單元，則容易造成的最終單元的冗余，增大計算規模。本文方法對每次單元細分加密數目進行控制，單元均勻細分的實際數目為：

5 自適應分析策略

對曲梁自由振動問題，利用上述基于振型超收斂拼片恢復解的有限元解誤差估計、網格細分加密方法，可以形成有效的網格自適應分析方法，最終可以得到優化的網格，并獲得該優化網格上滿足誤差限的各階高精度頻率和振型解答。對于振型，超收斂解u?較當前網格而下有限元解u h具有更高的收斂階，即u?比u h更接近精確解u，因此采用u?代u對u h進行誤差估計和控制，形成能量模形式的誤差估計；對于頻率，利用位移超收斂解計算Rayleigh 商[23]得到頻率的超收斂解。通過Rayleigh 商得出的頻率超收斂解比振型超收斂解具有更高的收斂階，本文通過估計和控制振型解答的誤差可保證頻率解答滿足誤差要求，如此可形成本文算法通過控制振型誤差的停機準則。基于有限元解的誤差估計進行網格細分加密，即可求得優化的網格和滿足誤差限的各階高精度頻率和振型解答，形成一套有限元自適應求解方案：

1)有限元解：對于曲梁振動問題，在當前網格π 上進行常規有限元計算，得到當前網格下特征對的有限元解(ωh,u h)；

2)振型超收斂解：利用有限元后處理超收斂拼片恢復方法，可得當前網格下振型的超收斂解u?；同時，可得超收斂解與有限元解之間的誤差估計值ξ；

3)網格細分加密：對于 ξ不滿足式誤差控制式(14)的單元，用網格細分加密方法將其細分，得到新的有限元網格，返回步驟1)；如果所有單元均滿足誤差限，則網格無需再細分，求解過程結束。

6 數值算例

本文方法已經編制Fortran 90程序，本節給出求解多種變截面變曲率梁面內和面外自由振動的數值算例，通過對比典型的拋物線曲梁、變截面變曲率梁、橢圓弧曲梁面內自由振動和拋物線曲梁、圓弧曲梁面外自由振動結果來驗證本文方法計算結果的精確性和適用性。本節所有算例均采用3次元，初始網格采用2 個單元，給定的初始誤差限為Tol=10?4，設定單元細分的極限數目為d=6。

例1.拋物線曲梁面內自由振動

考慮如圖2所示的拋物線曲梁，曲梁跨度L=5 m、高度h=4 m。

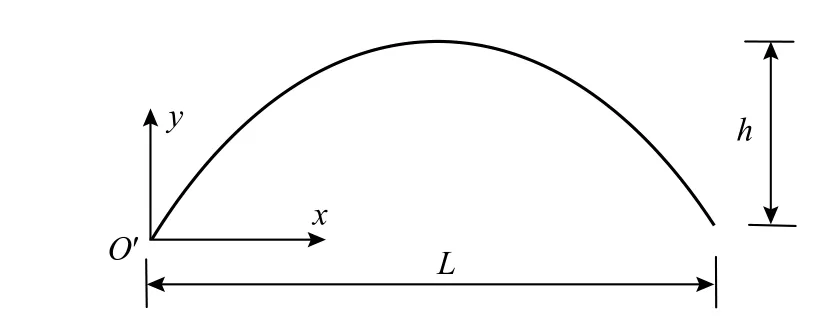
圖2 拋物線曲梁幾何模型Fig.2 Geometric model of parabolic curved beam

該曲線梁的拋物線方程為：

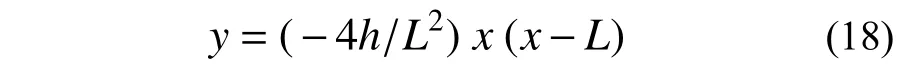
該曲線梁的基本參數如下：

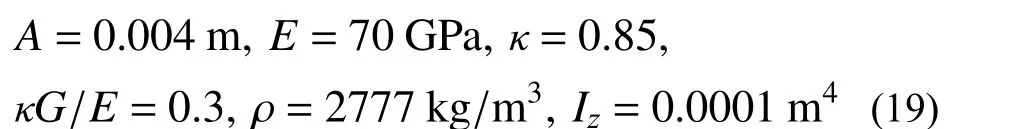
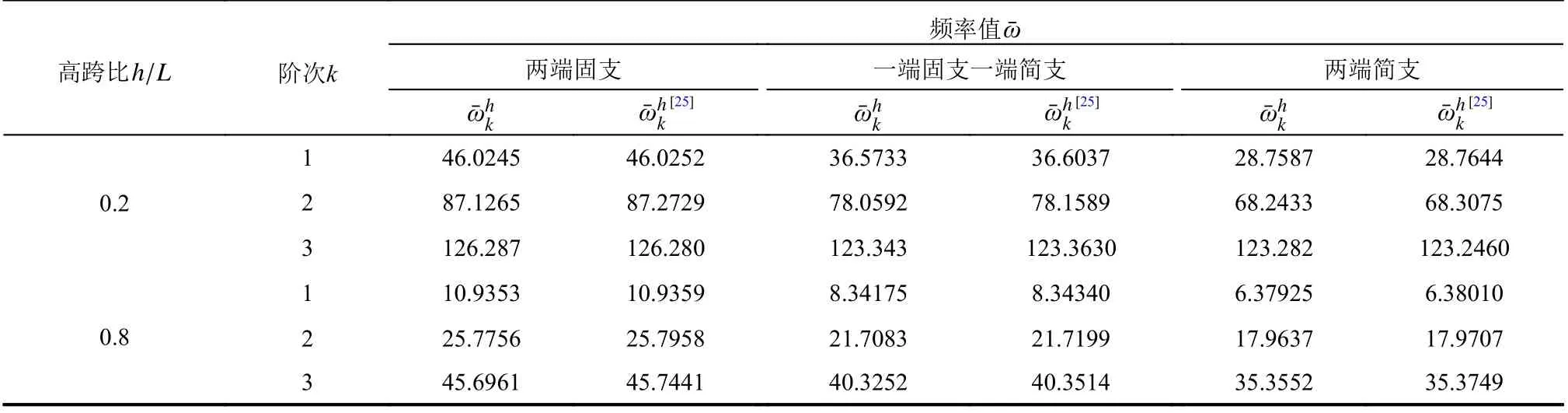
表1 拋物線曲梁面內自由振動無量綱頻率值Table 1 Non-dimensional frequencies of in-plane vibration of parabolic curved beam

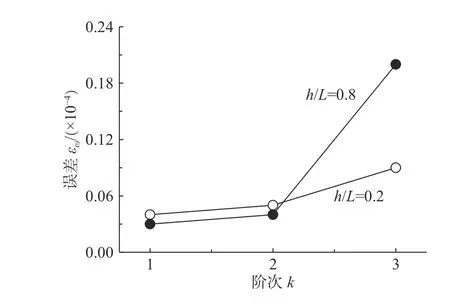
圖3 本文方法解答與密集網格高精度解的誤差Fig.3 Errorsof results of proposed method and highprecision solutionsunder dense mesh

圖4～圖6分別給出了本文方法求解兩端固支邊界、高跨比h/L=0.8情況下的前3階振型結果，并在橫坐標軸上標記出自適應網格的最終分布情況。為方便直觀顯示和對比分析，圖中振型結果均進行歸一化處理(令最大振型值為1)。可以看出，振型在兩固定端的位移均為0值；本文方法求解各階振型均劃分出非均勻網格，且在振型變化平緩區域使用稀疏網格、在振型變化劇烈處采用了相對細密的網格，避免了全域使用一致細密網格的冗余性。

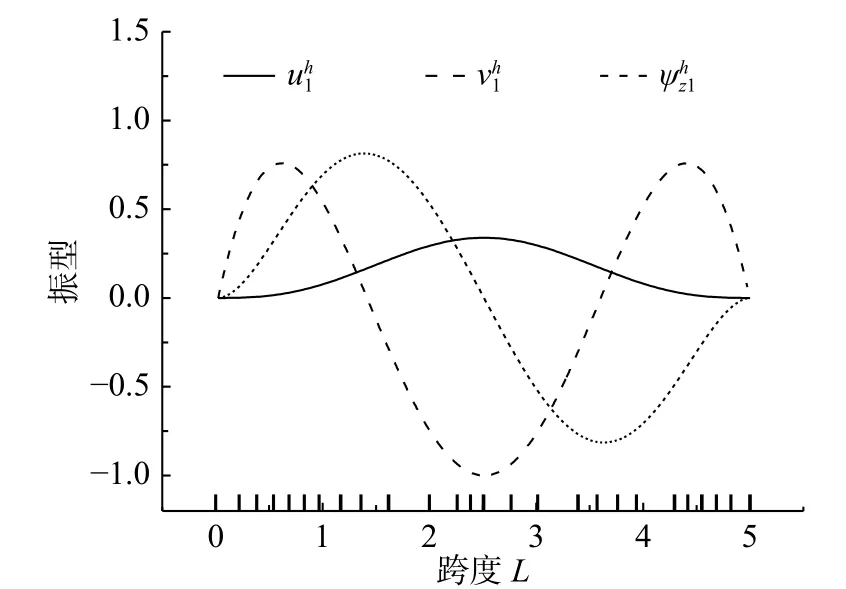
圖4 第1階振型(uh1,vh1,ψ hz1)Fig.4 First order vibration mode(uh1,vh1,ψ hz1)

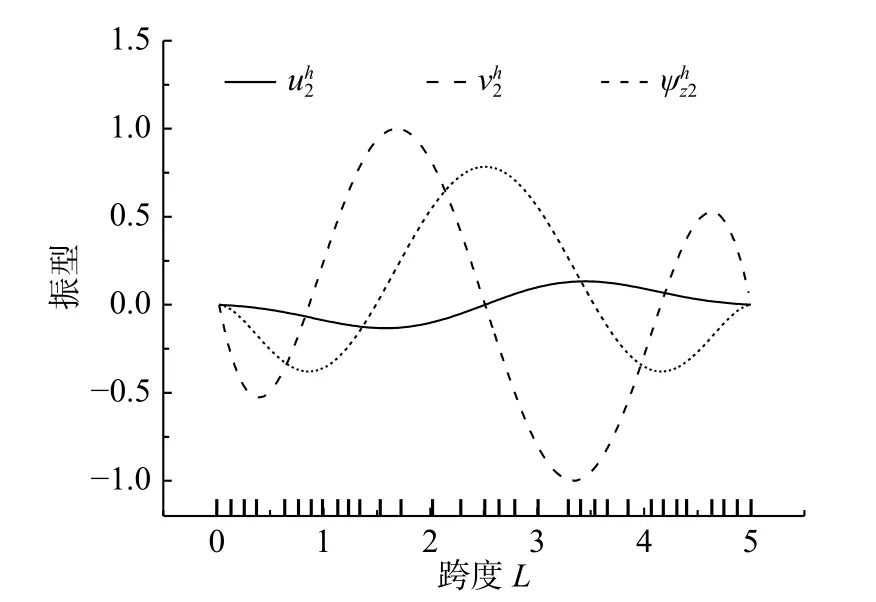
圖5 第2階振型(uh2,vh2,ψhz2)Fig.5 Second order vibration mode (uh2,vh2,ψ hz2)

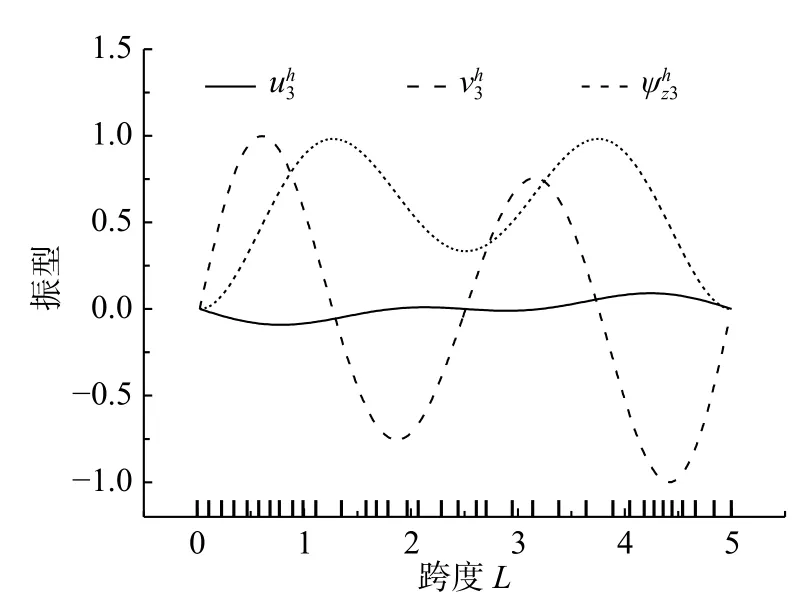
圖6 第3階振型Fig.6 Third order vibration mode (uh3,vh3,ψ hz3)

例2.變截面變曲率梁面內自由振動

考慮圖7所示的變截面變曲率梁，曲梁兩端為固支邊界條件、跨度為L。

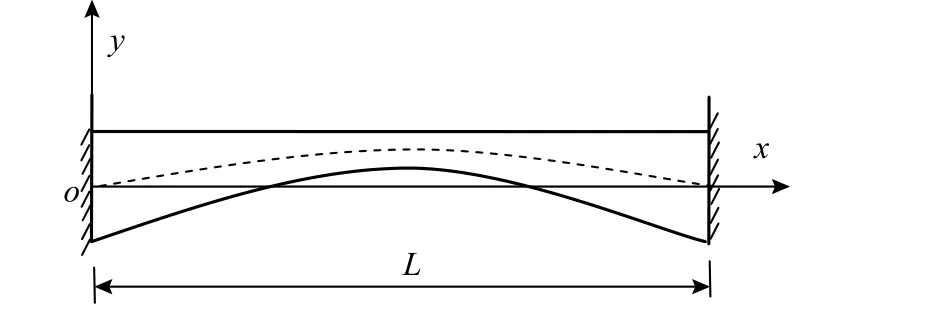
圖7 變截面變曲率梁幾何模型Fig.7 Geometric model of non-uniform and variable curvaturecurved beam

使用本文方法連續求解該曲梁面內自由振動的連續前4階特征對，計算頻率值列于表2。文獻[26]發展基于Wittrick-Williams算法的動力剛度法求解該問題，解答如表2所示，可以看出本文求解結果與該動力剛度法結果吻合較好，檢驗了本文方法對同時變化截面和曲率形式梁的面內自由振動求解的有效性。

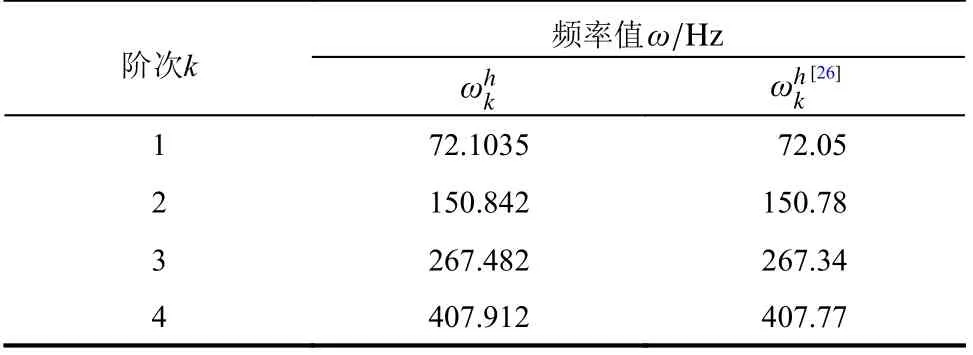
表2 變截面變曲率梁面內自由振動頻率值Table 2 Frequencies of in-plane vibration of non-uniform and variable curvature curved beam

例3.橢圓弧曲梁面內自由振動

例4.拋物線曲梁面外自由振動

考慮例1中圖2所示拋物線曲梁的面外自由振動，拋物線方程同式(18)，該曲線梁的基本參數為：

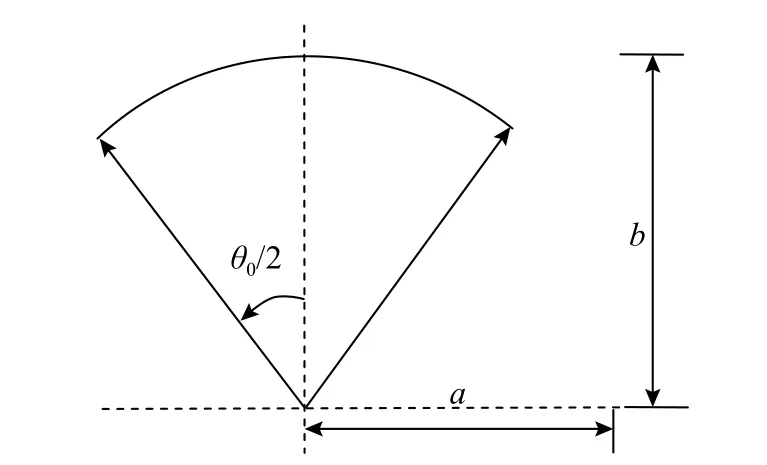
圖8 橢圓弧曲梁幾何模型Fig.8 Geometric model of of elliptic curved beam

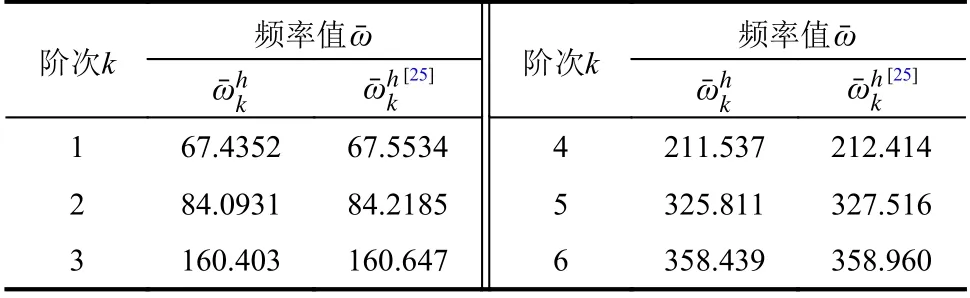
表3 橢圓弧曲梁面內自由振動無量綱頻率值Table 3 Non-dimensional frequenciesof in-plane vibration of elliptic curved beam

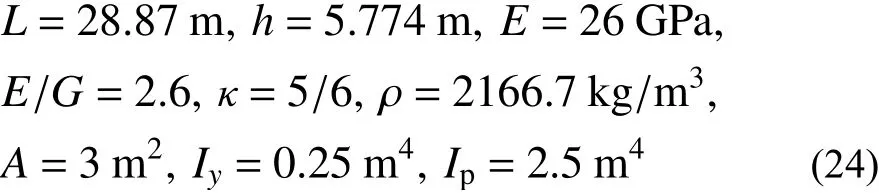
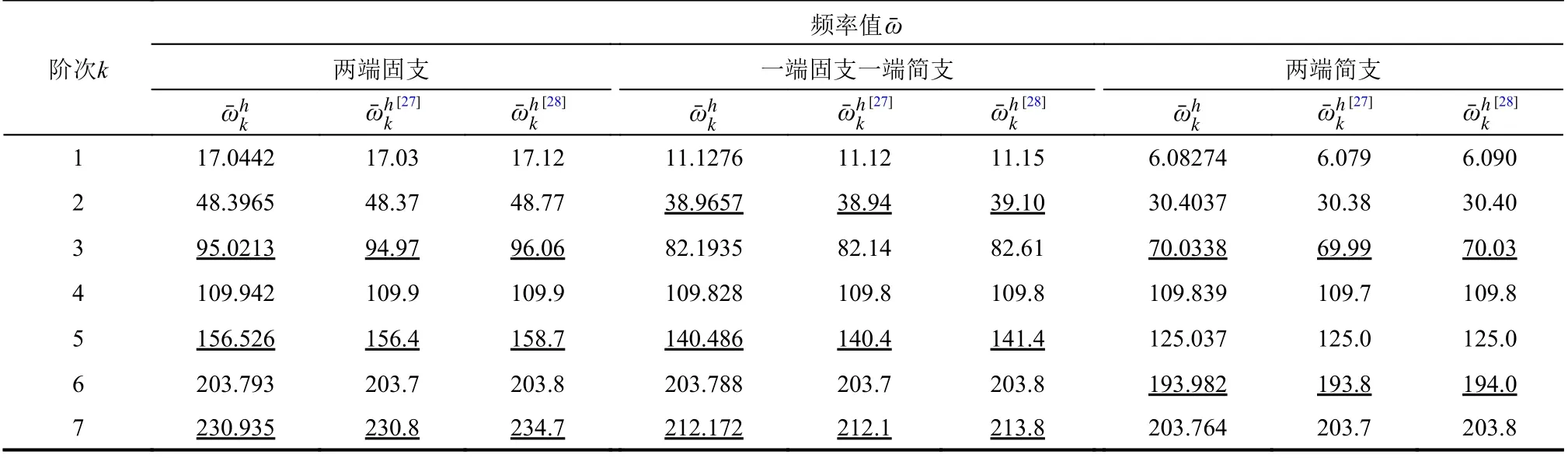
表4 拋物線曲梁面外自由振動無量綱頻率值Table 4 Non-dimensional frequencies of out-of-plane vibration of parabolic curved beam

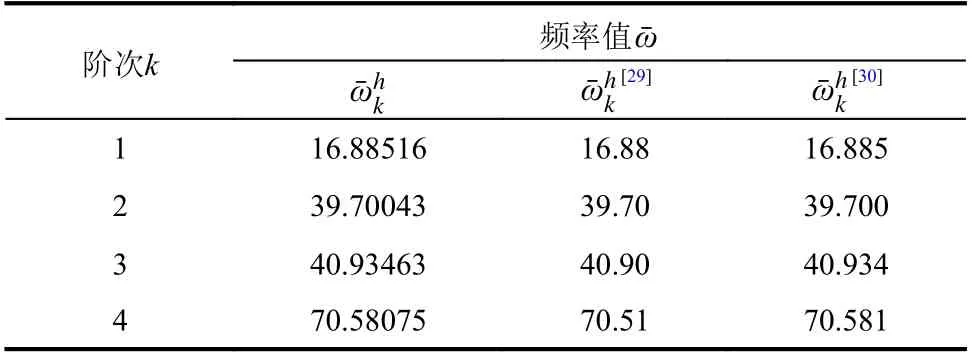
表5 圓弧曲梁面外自由振動無量綱頻率值Table5 Non-dimensional frequenciesof out-of-plane vibration of circular curved beam

例5.圓弧曲梁面外自由振動

考慮圖10所示兩端固支圓弧曲梁，圓弧角度為 θ0，梁橫截面為圓形。

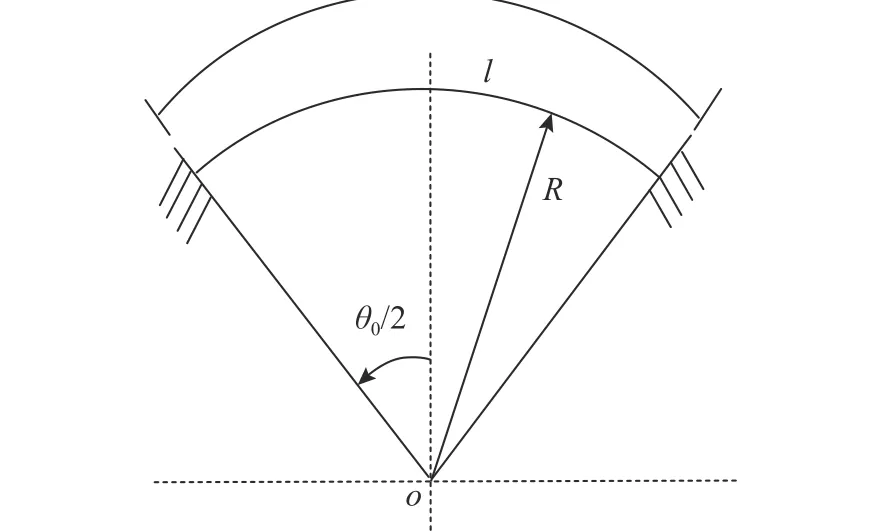
圖10 圓弧曲梁幾何模型Fig.10 Geometric model of circular curved beam

該曲線梁的基本參數為：

7 結論

本文研究工作的主要結論和計算方法潛力可總結如下：

(1)本文提出變截面變曲率梁面內和面外自由振動振型的有限元后處理超收斂拼片恢復方法，建立各階振型的超收斂解，基于振型超收斂解進行網格自適應加密，求解得到優化的網格與滿足用戶給定誤差限的頻率和振型。

(2)本文算法具有通用性，分析了不同曲線形態、多類邊界條件、變截面、變曲率形式的曲梁振動問題，可推廣到一般形式結構和固體變形場有限元解的超收斂計算及自適應分析。

(3)本文方法具有應用分析含裂紋損傷曲線形桿件振動和穩定等工程實際問題的潛力，獲得損傷缺陷下的高精度振型和失穩模態，為分析裂紋損傷對曲線形桿系結構的影響提供可靠解答。