基于剛柔耦合的航炮炮口振動研究
劉圣強,殷鵬賢,陳 雷,李 利
(鄭州機電工程研究所,河南 鄭州 450000)
0 引 言
射擊精度是考核航炮射擊性能的一項重要指標,除了內外彈道因素對航炮射擊精度有影響外,航炮炮口的振動也是重要的影響環節,有時可能是首要影響環節[1]。本文基于有限元理論對航炮身管和炮口夾箍等易變形的構件進行模態分析并得到身管和炮口夾箍的模態中性文件。在此基礎上,利用多體動力學理論在動力學仿真軟件ADAMS 中構建航炮的剛柔耦合動力學虛擬樣機模型,分析了不同射速下航炮連發射擊時炮口的動態響應[2]。
1 剛柔耦合模型的建立
在進行航炮炮口振動規律的研究時,把與炮口擾動關系緊密、易變形的身管、炮口夾箍作為柔性體,把其他變形量小、與炮口振動無關的構件處理成剛體,利用有限元理論在Ansys 中對其柔性體構件建立模態中性文件[3],利用多體動力學理論在動力學仿真軟件ADAMS 中建立剛柔耦合模型[4 –5],進行仿真計算,得到航炮自動機連續射擊時炮口的振動規律。
在ADAMS 中,分別以剛體質心的笛卡爾坐標、能夠反映剛體位移的廣義歐拉角以及歐拉角作為物體坐標系的廣義坐標:
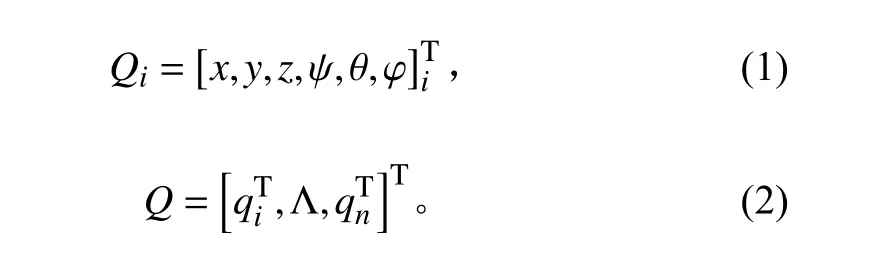
系統的動力學方程采用拉格朗日算法:
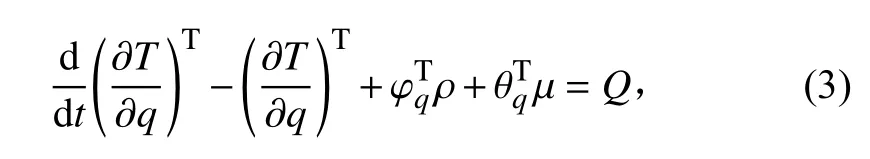
全約束方程為:

欠約束方程為:

式中:T,Q 分別為系統的動能和廣義力列陣;q,ρ,μ 分別為系統廣義坐標列陣,完全約束拉式列陣和不完全約束拉式列陣[6]。
約束多體動力學方程如下:
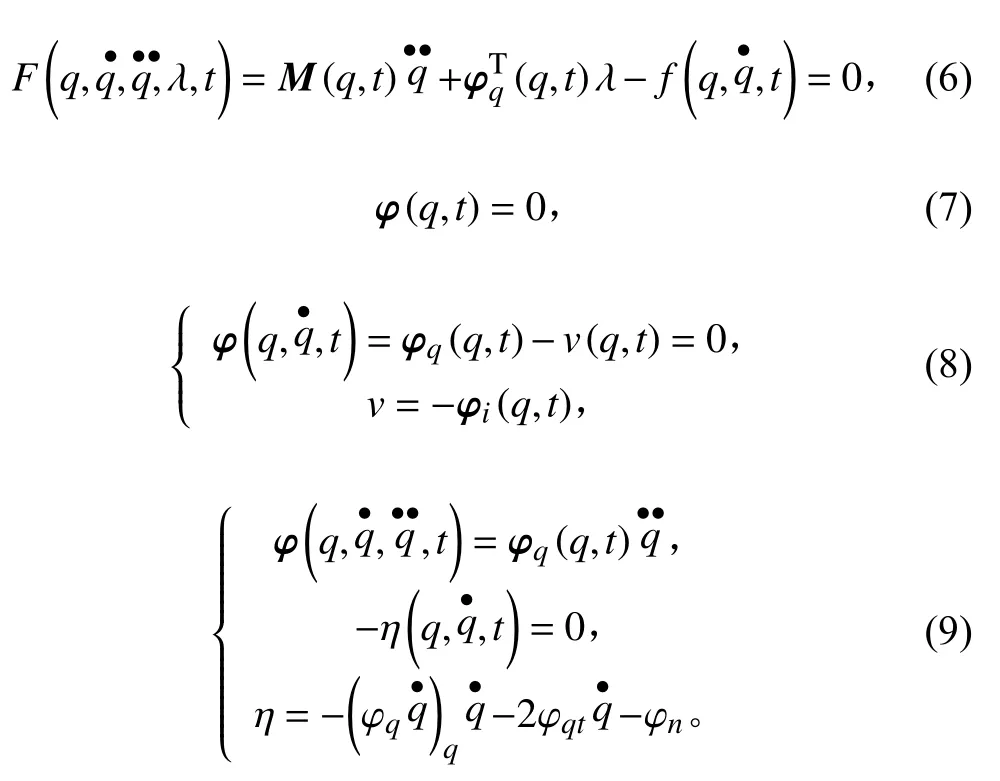
通過上述方程,分別給出了ADAMS 中的坐標定義、動力學方程以及多體動力學各參數之間的函數相關量,因此可利用ADAMS 軟件對模型的運動參數和力參數進行求解[8]。
ADAMS 建立剛柔耦合虛擬樣機模型的流程如圖1所示。
蚜蟲喜歡群居葉背、花梗或嫩莖上,吸食植物汁液,分泌蜜露。被害葉部變黃,葉面皺縮卷曲。嫩莖、花梗被害呈彎曲畸形,影響開花結果,植株生長受到抑制,甚至枯萎死亡。
航炮射擊過程中,身管和炮口夾箍的彈性變形對射擊精度的影響不容忽視,因此本文主要對身管和炮口夾箍這兩個構件建立柔性體,在剛柔耦合模型中采用模態法來描述柔性體的變形。
1.1 柔性體-身管的模態計算與剛性區域的建立
為了方便與其他的剛體或柔性體建立連接關系、載荷、接觸或者約束,在柔性體建模時需要建立可與外界進行信息交換的剛性節點[9]。
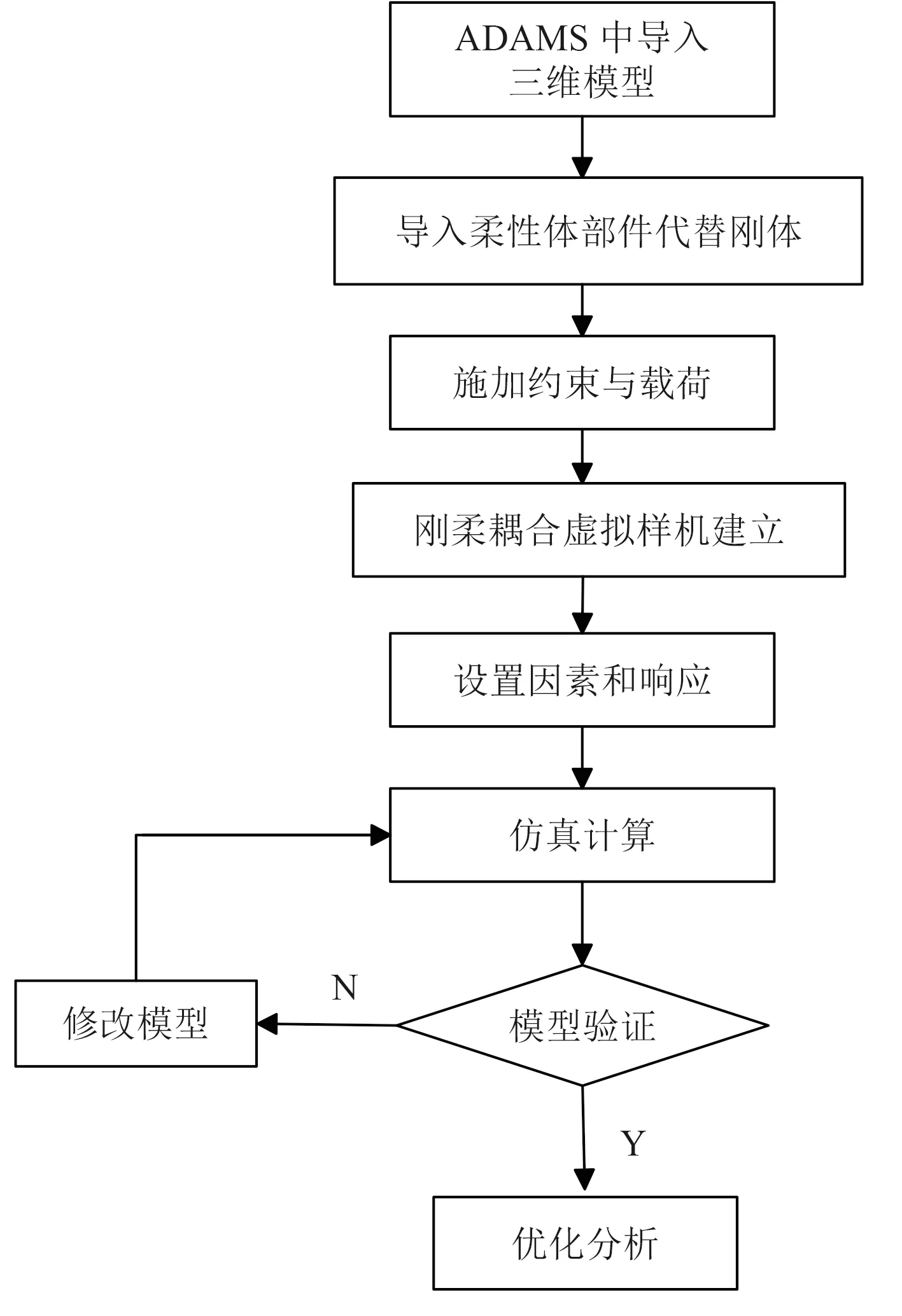
圖1 ADAMS 中剛柔耦合建模流程Fig.1 Modelling flow charts of rigid-flexible coupling in ADAMS
在Ansys 中計算得到的柔性體-身管的各階模態,身管、炮口夾箍的材料為鋼,其密度為7.85×103kg/m3,彈性模量為 E=210 GPa,泊松比為0.31。
在身管和炮口夾箍的有限元模型中,利用有限元理論計算得到身管和炮口夾箍各階模態的固有頻率。目的在于:一方面得到身管-炮口夾箍組件各階模態的固有頻率,與自動機的射頻進行比較,觀察在射擊過程中是否發生共振,來驗證身管結構設計的合理性;一方面得到身管-炮口夾箍組件各階模態的振型,為后續結構的改進提供理論依據[10]。
身管主要與炮口夾箍、炮尾、前后襯套連接,因此有4 個界面節點(即剛性節點)。柔性身管利用固定副實現剛性節點與剛性炮尾、剛性襯套以及柔性炮口夾箍的連接,保證了載荷(炮膛合力)均布分在身管后端面的每個節點上。其他柔性構件的連接也采用上述方式,由于建立剛性節點的方法相同。柔性體身管在Ansys 中的剛性區域建立如圖2 所示。
計算身管-炮口夾箍組件的模態時,根據航炮自動機的實際支撐方式對其添加約束,身管-炮口夾箍組件的約束方式為后端面固定,其約束方式如圖3 所示:
通過分析可以得出以下結論:
1)身管-炮口夾箍的第1 階和第3 階模態以彎曲振型為主,第2 階和第4 階模態以扭轉為主。
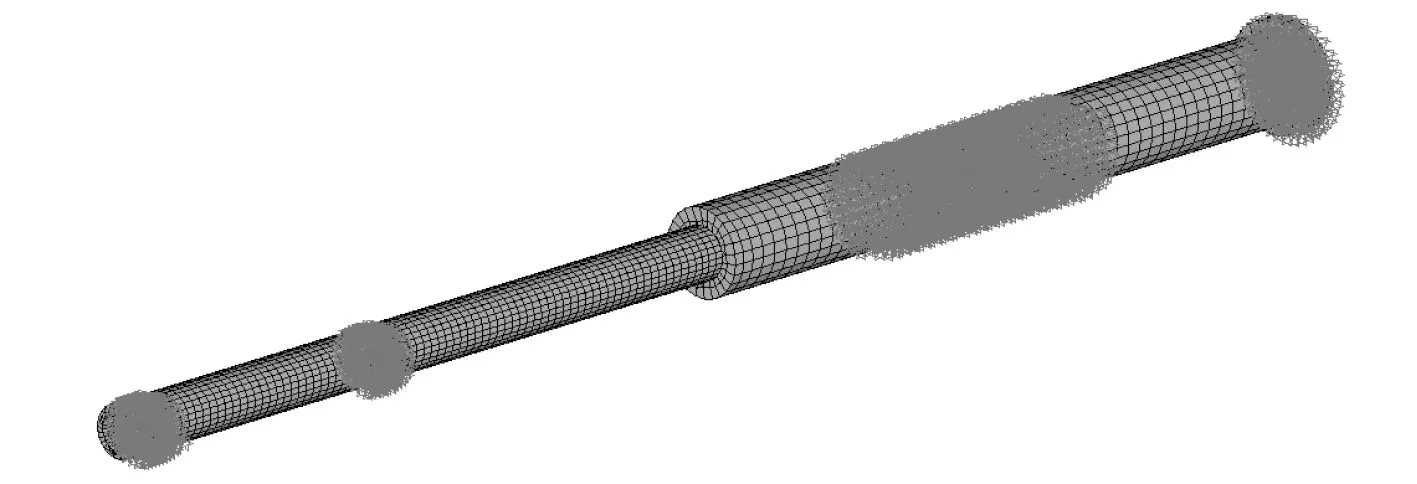
圖2 Ansys 下身管剛性區域Fig.2 Rigid region of gun tube in Ansys

圖3 身管-炮口夾箍組件的約束方式Fig.3 Restraint mode of gun tube-muzzle clamp
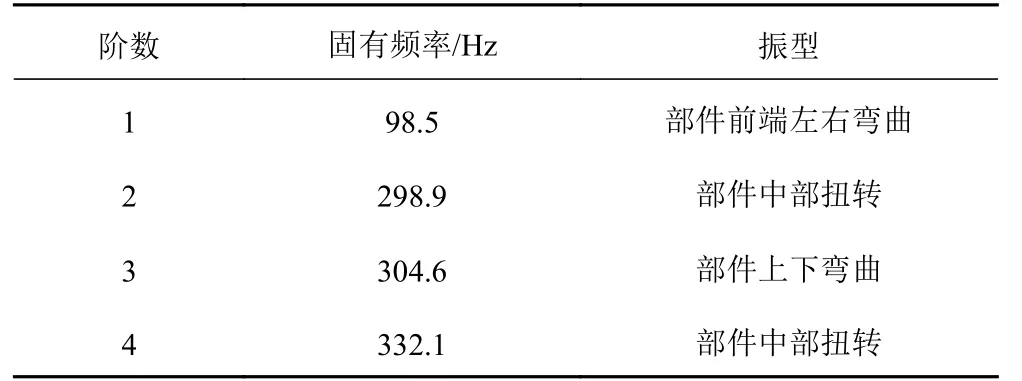
表1 身管-炮口夾箍1~4 階模態的頻率與振型Tab.1 4 extended modal frequency and shape of gun tube - muzzle clamp

圖4 身管-炮口夾箍前4 階振型Fig.4 4 extended modal shape of gun tube - muzzle clamp
2)航炮自動機的射速為3000 發/分,振動頻率為50 Hz,由表1 得到該身管-炮口夾箍組件的前4 階模態振動頻率范圍為98–333 Hz。因此在正常射擊工況下,該結構各階頻率遠離了載荷激勵頻率,其本體不會出現共振情況,其他頻率皆分布在高頻段,這說明了身管-炮口夾箍頻率結構設計的合理性。
1.2 炮口夾箍的模態計算與剛性區域建立
利用Ansys 計算得到炮口夾箍在約束狀態下前6 階模態的固有頻率,約束方式為一端固定,與身管接觸的孔為徑向方向位移約束,約束方式如圖5所示。
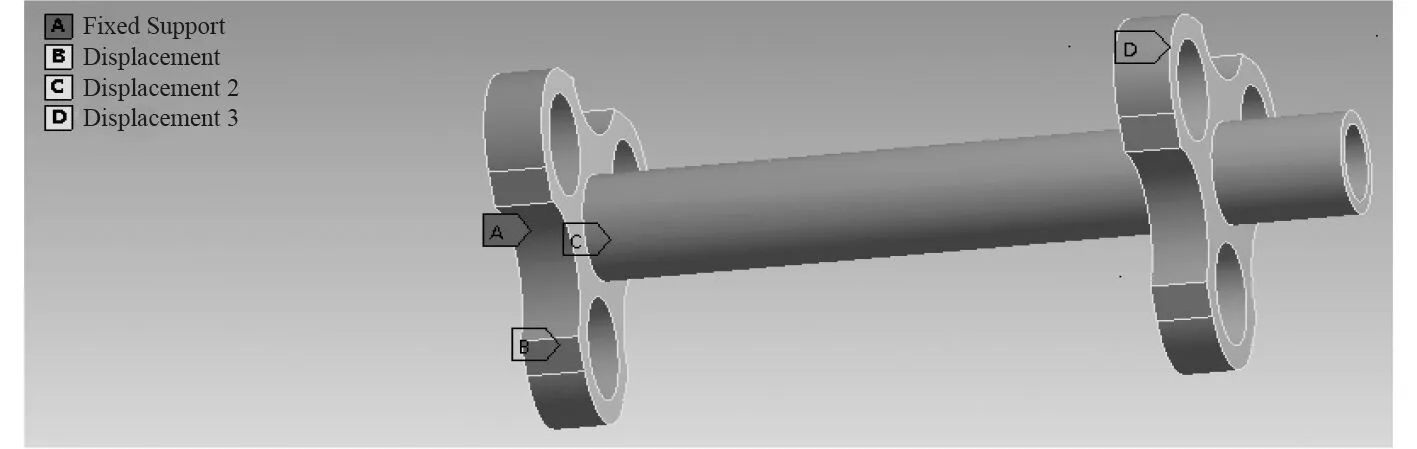
圖5 炮口夾箍組件的約束方式Fig.5 Restraint mode of muzzle clamp
炮口夾箍前6 階模態的固有頻率如表2 所示,振型圖如圖6 所示(頻率相同的振型已整合)。
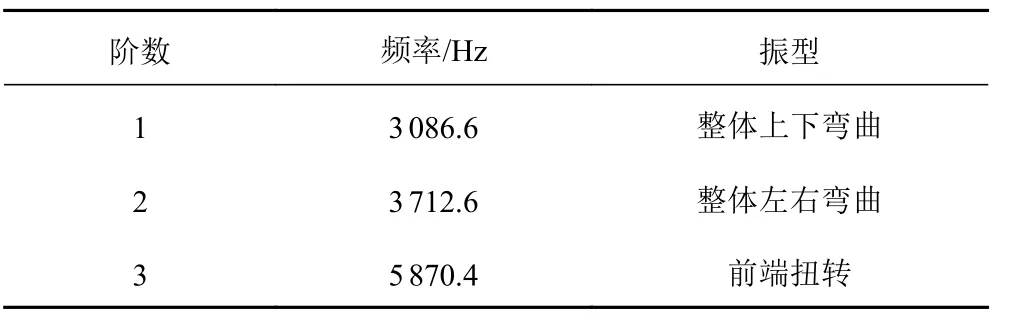
表2 炮口夾箍1~6 階頻率與振型Tab.2 6 extended modal frequency and shape of muzzle clamp
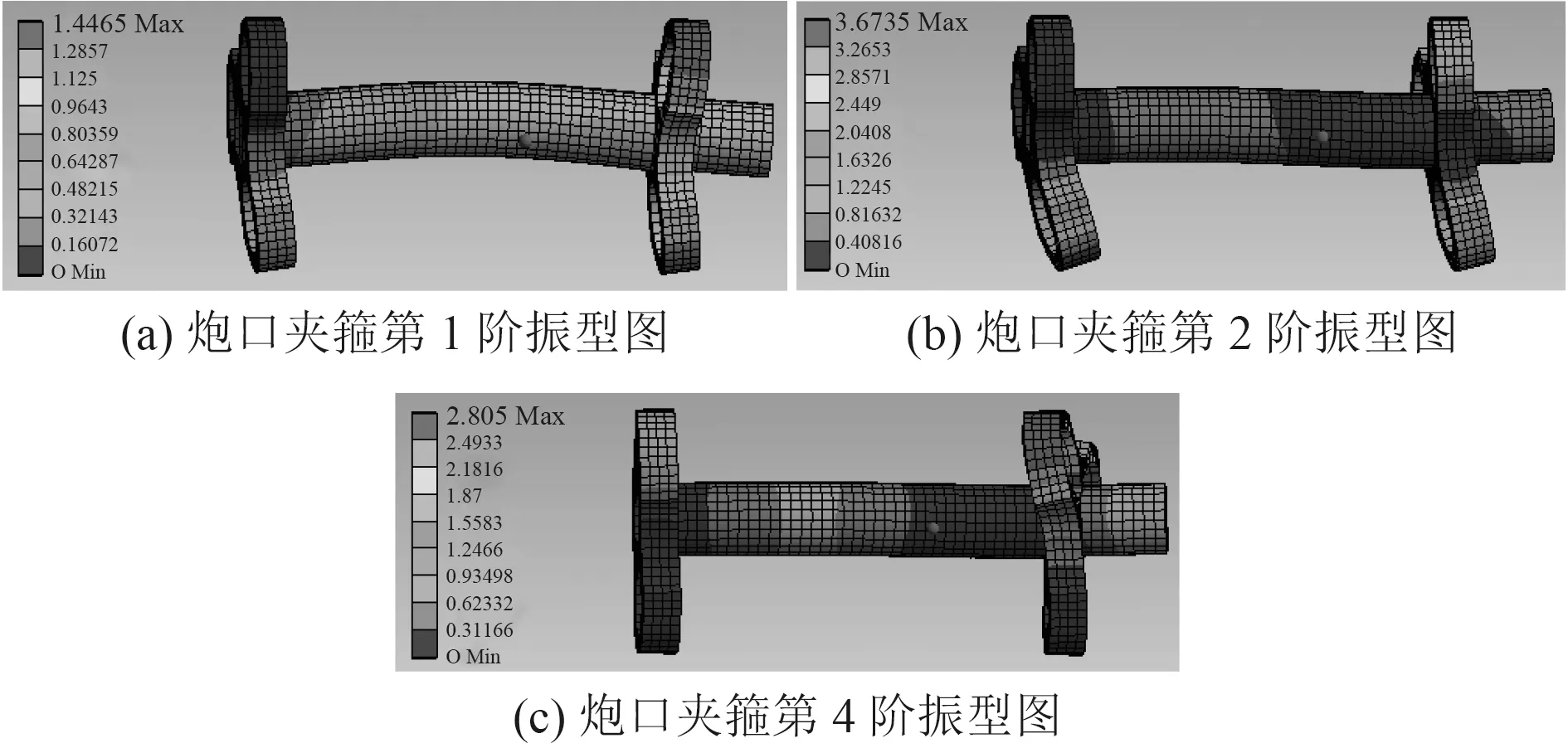
圖6 炮口夾箍各階振型Fig.6 Modal shapes of muzzle clamp
炮口夾箍有6 個界面節點(即剛性節點)分別與3 根身管相連。柔性體炮口夾箍在Ansys 中的剛性區域如圖7 所示。
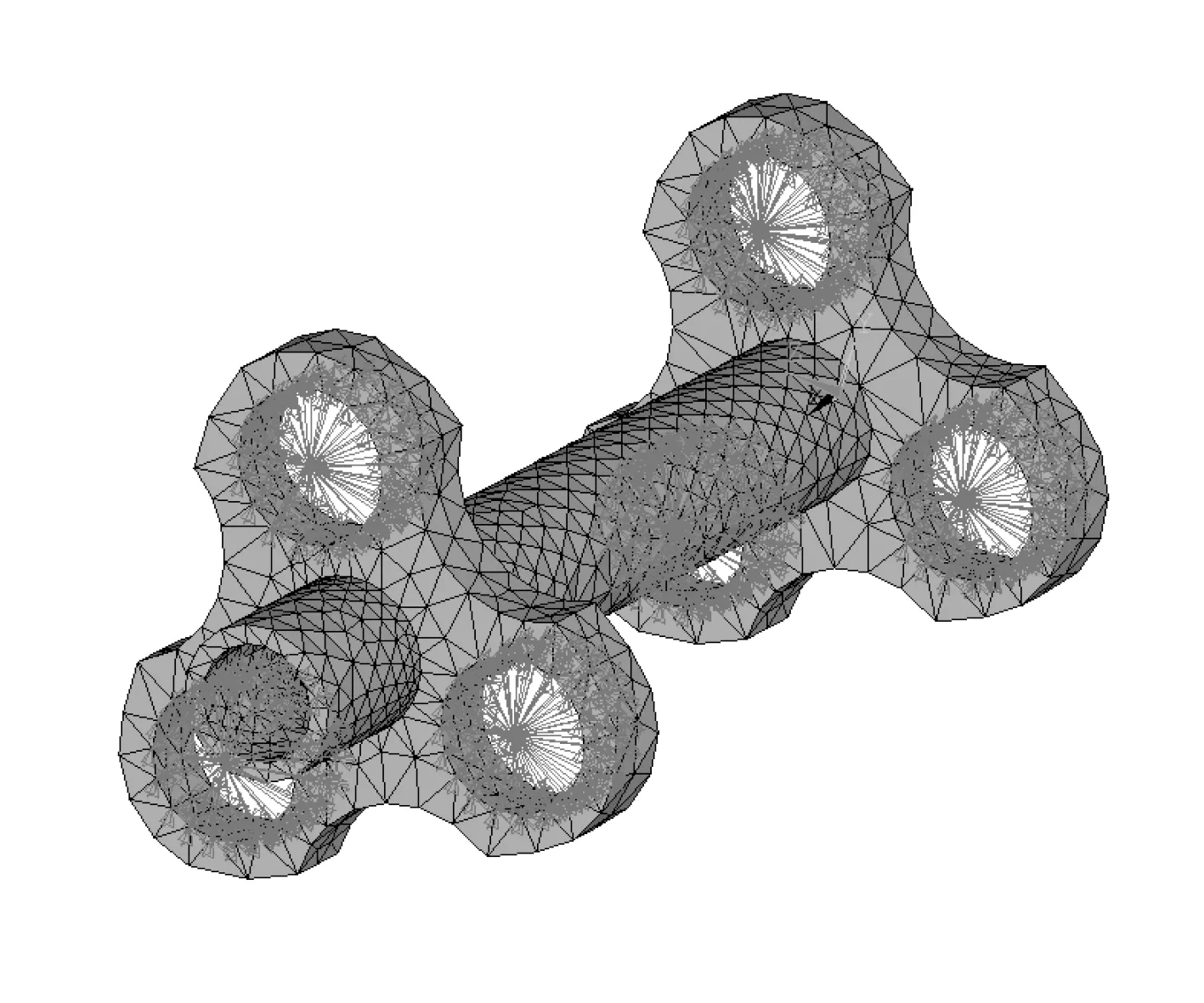
圖7 炮口夾箍剛性區域的建立Fig.7 Establishment of muzzle clamp rigid region
通過以上分析可以得出結論:炮口夾箍在約束狀態下的前3 階振動頻率遠遠大于載荷激勵頻率,說明了炮口夾箍結構設計的合理性。
2 航炮剛柔耦合虛擬樣機的建立
將建立好的柔性體(身管和炮口夾箍)導入動力學仿真軟件ADAMS 中,建立航炮虛擬樣機模型。剛體與柔體的約束一般都可以直接用ADAMS 中的常用約束副來完成,可以通過約束柔性體上的剛性節點和剛體上的marker 點實現的。剛體與柔體的接觸在ADAMS 中一般選擇flexible-solid 接觸來實現。
自動機剛柔耦合虛擬樣機中剛體和柔性體約束如表3所示,得到自動機剛柔耦合虛擬樣機模型如圖8 所示。

表3 剛體和柔性體約束列表Tab.3 Constraint list of rigid body and flexible body

圖8 自動機剛柔耦合虛擬樣機模型Fig.8 Virtual prototype model of rigid-flexible coupling of automaton
3 計算結果分析
根據建立的自動機剛柔耦合虛擬樣機,分析不同射速下炮口的橫向振動位移和縱向振動位移,得出炮口振動隨自動機射速的變化規律,為提高航炮的射擊精度提供理論支持。由于剛柔耦合模型約束關系復雜、計算量大,故選擇航炮理論射速周邊的射速進行計算。選擇航炮射速5000 發/分、6000 發/分、7000 發/分的計算結果進行討論。
自動機穩定射擊狀態下,炮口縱向振動位移最大值隨射速的提高明顯增加,從5000 發/分到6000 發/分,其縱向振動位移的最大值增加了約60%;從6000 發/分到7000 發/分,其縱向振動位移的最大值增加了約70%。自動機穩定射擊狀態下,炮口的橫向位移值同樣隨射速的提高出現明顯增加,從5000 發/分到6000 發/分,炮口橫向位移的最大值增加了約1.2 倍,但其位移值較小可以忽略;從6000 發/分到7000 發/分,其橫向位移的最大值增加了約3 倍,雖然橫向位移量較小以至于可以忽略,但隨著射速的繼續增加,其橫向位移最大值達到不可忽略的程度,將會對航炮的射擊精度造成影響。

圖9 不同射速下炮口橫向/縱向位移-時間曲線Fig.9 Transverse/longitudinal displacement-time curves of the muzzle at different firing rate
4 結 語
本文運用有限元理論對影響炮口振動的柔性體構件建立模態中性文件和其對應的剛性區域。在動力學仿真軟件中得到自動機剛柔耦合虛擬樣機模型并進行仿真計算,得到航炮在不同射速下炮口振動位移的變化規律,為航炮射擊精度的研究和飛機總體的設計提供理論依據。

