基于PFC2D的某礦區反傾巖質邊坡穩定性分析

何 倩，薛喜成

(1.徐州中國礦大巖土工程新技術發展有限公司，江蘇 徐州 221000；2.西安科技大學地質與環境學院，陜西 西安 710054)

0 引 言

目前，對于邊坡穩定性評價的方法主要有定性分析和定量評價[1]，定量評價多采用極限平衡法和數值分析法，極限平衡法通常不能真實地反映邊坡失穩時的應力場和位移場[2]，存在一定局限性，而數值分析法越來越受到國內外學者的重視，常見的數值模擬方法有有限差分法、有限單元法和離散單元法。顆粒流法(Particle Flow Code，PFC)是基于離散單元模型框架的一種定量評價方法，于1971年Cundall[3]首次提出，適用于研究非連續介質力學問題，可體現多相介質的不同物理關系，顆粒之間可彼此分離，能夠反映巖塊或土體之間的滑動、平移和分離等大位移。通過定義顆粒為有質量和表面的剛性體和顆粒之間的接觸模型，模擬顆粒的運動以及顆粒之間的相互作用，反映運動機理、過程和結果[4]。賀續文等[5]采用PFC建立含密集節理的巖體邊坡模型，研究了節理連通率對邊坡破壞形式的影響。Camones等[6]利用PFC研究裂隙巖體的機理以及裂紋擴展在巖質邊坡階梯狀滑移中的作用。張小勇等[7]采用PFC建立順層頁巖邊坡模型，分析其穩定狀態并對其失穩過程進行研究。楊天鴻等[8]研究了露天礦邊坡的動態穩定性評價分析預測方法。王培濤等[9]將強度折減法引入離散元法中研究邊坡穩定性，將顆粒間粘結強度及摩擦系數進行折減，對邊坡定性預測并監測其破壞失穩過程。Zheng等[10]利用UDEC模擬反傾層狀巖體邊坡的傾倒破壞，研究影響邊坡穩定的因素。張志飛等[11]基于PFC模擬反傾層狀巖質邊坡變形破壞過程，分析變形破壞機制的影響。本文采用離散元二維顆粒流程序(PFC2D)，研究某反傾巖質邊坡的穩定狀態，并預測其失穩過程，分析破壞過程，為后期邊坡加固處理以及礦區開采安全提供參考。

1 工程地質概況

礦區位于燕山山前平原與燕山山脈接壤的地帶，采礦方法為臺階式露天開采。由于石灰礦開采的影響，使地層長期緩慢移動，坡體周圍分布不同程度的地表裂縫，一些甚至出現了沿傾向的裂縫，使沿走向的裂縫連通起來，說明裂縫對地層穩定的影響在逐漸加劇，對礦區安全開采極為不利。礦區內出露地層主要為奧陶系、石炭系、二疊系巖層及第四系沖洪積、殘坡積物，礦區內發育一定規模的斷層，礦體賦存于奧陶系上馬家溝組中段地層中，邊坡上部巖性主要為淺灰～土黃色泥質灰巖，中下部為灰～淺灰褐色厚層狀白云質灰巖和豹皮狀灰巖。邊坡示意見圖1。由現場調查分析，該邊坡坡頂存在拉張裂縫，邊坡產狀SSE167°∠60°，坡面存在少量破碎巖體，易發生巖體滾落。

圖1 邊坡示意

2 邊坡模型的建立

2.1 單軸壓縮試驗標定

PFC中巖體的參數是細觀參數，這些參數與實際材料的物理力學參數沒有確切的對應關系，不能將試驗得到的宏觀力學參數直接應用于PFC的模擬之中。目前，在PFC中一般采用試錯法進行細觀參數的確定，其確立的過程需要根據巖石的彈性模量、抗壓強度、泊松比等宏觀參數進行不斷地調整，使細觀參數模擬的結果與巖石的宏觀參數相對應，此時得到的顆粒細觀參數就是邊坡的穩定性分析時所需要的細觀參數。

采用PFC內置的單軸壓縮模擬程序確定顆粒的細觀參數[4，12]，顆粒的半徑越小，越接近真實的情況。但受限于計算機的運行速度及內存容量等因素，可適當調整顆粒半徑[13]，單軸壓縮顆粒半徑與后續邊坡模型顆粒半徑一致。剛度模型采用線性剛度模型，滑動模型采用摩爾-庫倫模型，粘結模型采用平行粘結模型。通過巖體的物理力學參數標定，得到PFC模型細觀參數(見表1)。

表1 PFC模型細觀參數

通過單軸壓縮試驗得到邊坡巖體的應力應變關系見圖2。計算得到數值模擬單軸壓縮試驗下巖體的彈性模量和抗壓強度的模擬值，與宏觀力學試驗實測值對比見表3。從表3可知，模擬值與實測值的誤差百分比在2%左右[14]，符合數值模擬要求，可用于后續的邊坡穩定性分析之中。

圖2 應力-應變關系

表2 數值模擬值與宏觀力學實測值對比

2.2 邊坡數值模型建立

本文采用刪除法建立基于PFC2D軟件的邊坡模型[4，12]，具體步驟如下：①在AutoCAD中使用多線段命令繪制邊坡的幾何模型，邊坡模型寬330 m，高170 m，保存為DXF格式文件；②在PFC2D中通過Geometry import命令導入DXF文件并通過wall命令生成墻體，使用ball distribute命令在矩形范圍內生成一定半徑范圍的顆粒集合，刪除邊坡墻體外的多余顆粒；③對填充好的邊坡模型中的顆粒進行分組并進行初始化應力場，設置循環為最大不平衡力達最大接觸力的1.0×10-5時顆粒集合達到平衡狀態，消除懸浮顆粒；④設置邊坡模型的頂面為自由面，將底面及左右兩側采用fix命令進行剛性墻約束，生成邊坡模型。顆粒之間采用平行粘結接觸，粒徑范圍0.4～0.5 m之間，共生成顆粒49 432個。

在泥質灰巖層中布置4個測量圓，從坡腳至坡頂坐標分別為測量圓1(207，70)、測量圓2(235，100)、測量圓3(265，127.5)和測量圓4(294.2，149)，監測記錄這些位置在坡體滑動過程中的應力和孔隙率的變化狀態，并對圖中A～H顆粒X方向位移進行監測。監測點A、B在邊坡前緣，監測點C、D在邊坡中前部，監測點E、F在邊坡中后部，監測點G、H在邊坡后緣。建立的邊坡模型見圖3。深色顆粒為白云質灰巖層，淺色顆粒為泥質灰巖層。

圖3 邊坡離散元模型(單位：m)

3 巖質邊坡穩定性分析

3.1 邊坡運動特征

在模擬時，對邊坡施加重力作用，同時對模型中顆粒的位移和速度清零，以便于后續對邊坡位移和速度的記錄，循環至邊坡達到穩定狀態并記錄邊坡破壞過程中的應力、孔隙率以及裂紋數量的變化情況。邊坡隨時步進行的破壞過程見圖4。從圖4可知：

圖4 邊坡破壞過程模擬

(1)計算運行至3×103時步時，邊坡在重力作用下整體發生向下的位移變形，邊坡滑體中上部巖體的抗剪強度較弱，巖體較破碎，顆粒發生局部剪切破壞，位移明顯，坡腳處顆粒累積一定壓力后發生位移，并且邊坡出現明顯的滑動帶，顆粒最大位移0.1 m。

(2)運行至3×104時步時，坡腳處受到滑體中部以及坡后緣處不斷累積的重力擠壓作用產生應力集中，坡體顆粒沖破坡腳的鎖固作用，顆粒向前滑出，坡體中后部巖體受到拉張作用產生1條明顯的拉張裂紋，出現變形破壞的趨勢，顆粒最大位移達2.18 m。

(3)運行至1.5×105時步時，邊坡中后部及后緣處拉張裂紋逐漸增加并逐步擴展，巖體間產生大的縫隙并失去支撐，變形加劇，坡腳發生擠壓破壞，顆粒滑出邊坡坡面，并逐漸在坡腳處堆積，顆粒最大位移達12.63 m。

(4)運行至5×105時步時，邊坡滑體部分不斷下滑，坡腳處顆粒滑出后逐漸堆積，坡體中部剪切破壞與后緣拉張裂縫相互貫通，變形嚴重，原邊坡后緣處一處平臺小邊坡的顆粒全部向前滑動，導致裂紋擴展，巖體破碎，顆粒堆積，顆粒最大位移達55.12 m。

(5)運行至1×106時步時，顆粒最大滑動距離達71.79 m，邊坡滑體相互貫通，向下滑移，最終坡體整體破壞。

圖5 邊坡位移時程

A～H監測點顆粒位移曲線見圖5。從圖5可知，邊坡顆粒在重力作用下同時發生位移，上層的顆粒產生的位移最大，而下層顆粒的位移相對較小，是由于坡體前緣巖體滑動，坡中部發生剪切破壞，后緣巖體失去支撐向下滑動，邊坡上部顆粒所受應力大于下部顆粒，導致邊坡上層顆粒的位移變化顯著，而下層顆粒位移較小，即顆粒B位移最大，顆粒A位移最小。邊坡前緣的顆粒較后緣的顆粒產生的位移大，是由于邊坡下部顆粒粘結破壞而向下滑動，導致上部顆粒失去支撐產生向下的加速度和動能，推動邊坡前部顆粒繼續向前滑動，因此前緣顆粒的位移較大，后緣顆粒位移相對較小，即顆粒B位移最大，顆粒G位移最小。邊坡位移曲線總體變化趨勢大致相同，隨著時間的推進，位移不斷增加，位移曲線的斜率先迅速增加，然后逐漸變緩，表明顆粒的位移速度先增加，后在摩擦力的作用下位移速度逐漸減小，與邊坡破壞的規律相符。

邊坡速度矢量見圖6。從圖6可知，運行至5×103時步時，邊坡坡體產生明顯的滑動帶，滑體部分產生一定速度，其中靠近滑動面下部顆粒的速度相對較大，最大速度為1.01 m/s；運行至1×105時步時，由于坡腳處遭受上覆巖體的重力作用和擠壓作用，最大速度出現在邊坡坡腳處，為2.36 m/s，而滑體與滑床接觸位置的顆粒速度相對較小，由于中部巖體較破碎，導致滑體中部速度明顯增加，平均速度0.8～1.0 m/s；運行至2×105時步時，邊坡滑體部分速度較均勻，平均速度0.5～1.0 m/s，而坡腳處顆粒受到壓力擠出，顆粒速度最大，為5.58 m/s，在邊坡中后部以及后緣處由于產生了拉張裂縫使巖體失去一定支撐，導致巖體在重力作用下發生傾倒，顆粒產生一定大小的速度，平均速度1.5～2.0 m/s，方向偏向于坡面內；運行4×105時步及至6×105時步時，滑體顆粒最大速度均出現在坡腳，分別為3.02 m/s和2.94 m/s，顆粒速度呈現出逐漸減小的趨勢，是因為邊坡上部顆粒受到下部的阻礙，將動能傳遞至坡腳顆粒，坡腳顆粒被上覆顆粒推出，但在摩擦力的作用下動能逐漸降低，速度逐漸減小；繼續運行至1×106時步時，顆粒平均速度減小至0.2～0.6 m/s，后緣處有個別顆粒速度相對較大，為1.36 m/s，是因為邊坡變形破壞過程中可能存在不穩定巖塊崩落等現象，導致速度突變。

圖6 邊坡速度矢量

3.2 巖質邊坡破壞機理

邊坡的破壞過程中設立測量圓監測邊坡滑動破壞過程中的應力變化，應力變化見圖7。從圖7可知，邊坡底部顆粒由于受到重力作用和擠壓作用，顆粒向下滑動并在坡腳堆積。測量圓1中X和Y方向的應力顯著增加，其中Y方向的應力主要來源于上覆土壓力；測量圓2處于邊坡中前部，由于受到上覆巖土層重力作用向下擠壓以及測量圓內的巖土層持續向下滑動的作用，使得圓內的應力不斷波動，但總體仍呈現下降的趨勢；測量圓3處于邊坡的中后部，上覆巖土層逐漸滑出測量圓范圍，所受的豎向壓力和擠壓力逐漸減小，因此測量圓內X和Y方向應力逐漸減小，最終當巖土體全部滑出測量圓范圍后應力趨近于零；測量圓4處于邊坡后緣頂部，邊坡頂部顆粒產生拉張裂縫并持續向下滑動，因此測量圓內顆粒應力明顯減小，最終趨于零。

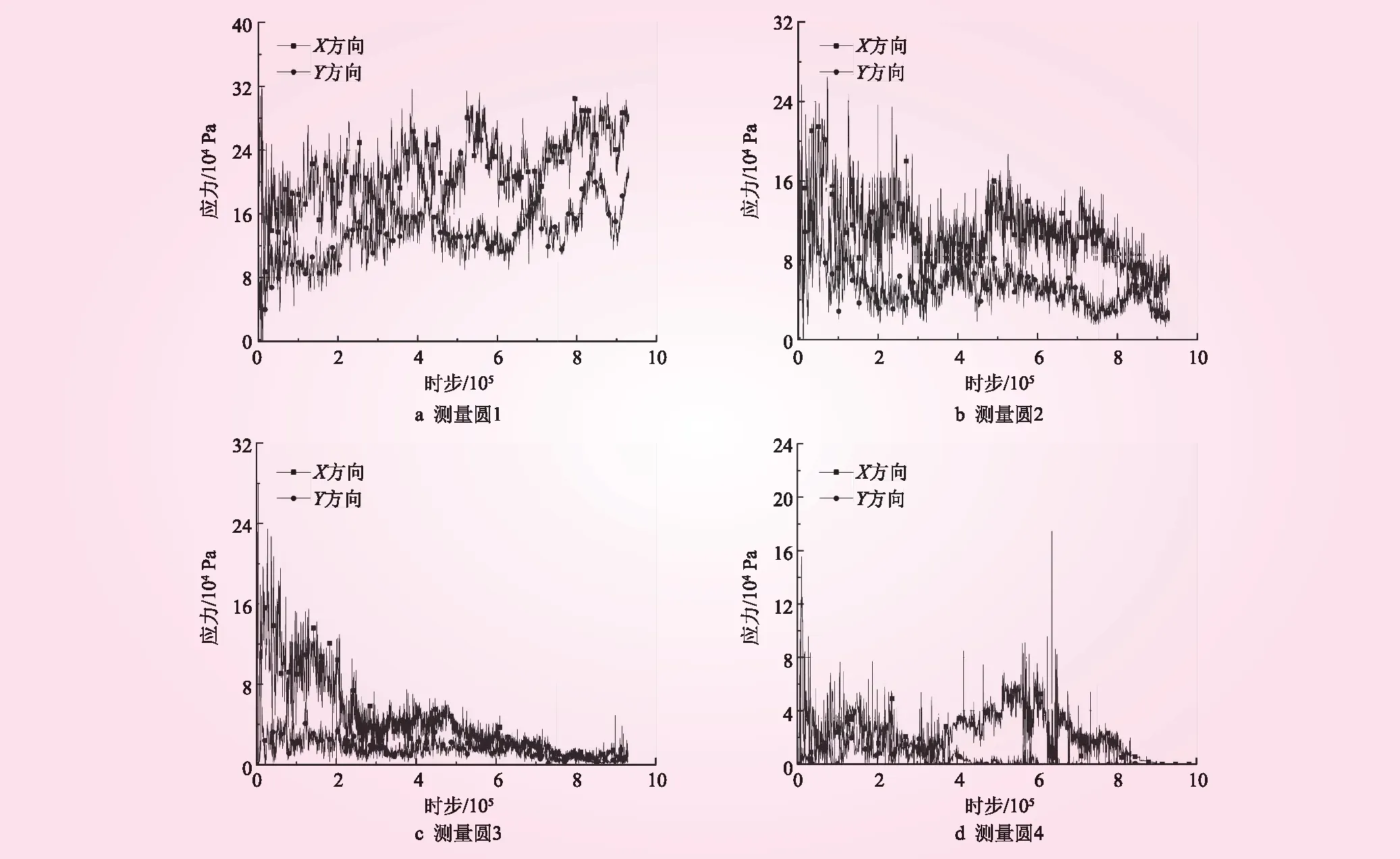
圖7 測量圓應力變化

不同位置巖體孔隙率隨時間變化見圖8。邊坡前緣測量圓1和邊坡中前部測量圓2中顆粒受到重力作用向下滑出，因此孔隙率在前期減小，但上覆巖體在失去下部支撐后迅速跟進，使得顆粒壓密，孔隙率反彈；邊坡中后部測量圓3處巖體剪切破壞，顆粒逐漸減少，孔隙率增大；坡頂處測量圓4中顆粒向下滑動直至全部滑出，孔隙率增大。

圖8 不同位置巖體孔隙率變化

在PFC軟件中，若顆粒間實際拉力或切向力大于相應的粘結強度，則顆粒間的粘結就會破壞，而發生破壞的粘結強度就是顆粒間產生的裂紋[4]。邊坡破壞過程中產生的裂紋數量隨時間變化見圖9。從圖9可知，裂紋數量隨時步先急劇增加后逐步減緩，邊坡坡腳首先產生大量細小裂紋，坡腳粘結破壞，邊坡中后部及坡頂處顆粒失去下部支撐向下滑動，導致坡體產生幾處貫通的拉張裂縫，隨后裂紋在邊坡滑體中逐步擴展，導致邊坡粘結大量破壞并最終失穩。最大裂紋數達3 723個，并且裂紋數量還在緩慢發展。

圖9 裂紋數量隨時間變化

4 結 語

本文采用離散元二維顆粒流程序(PFC2D)，對某礦區中的反傾巖質邊坡的穩定性進行研究，得出以下結論：

(1)對比邊坡巖土體標定的細觀力學參數與實測宏觀力學參數值，PFC建模所標定的細觀力學參數符合邊坡后續的穩定性分析的要求。

(2)該方法能夠在邊坡失穩破壞過程中直觀地反映邊坡顆粒運動過程以及運動過程中所搜索出的滑動面。

(3)邊坡中部破碎巖層首先發生剪切破壞，坡腳處顆粒因重力及上覆顆粒擠壓的作用，顆粒向外滑出，導致坡頂失去底部巖體的支撐產生拉張裂縫，顆粒向下滑動，最終邊坡整體失穩破壞為傾倒失穩破壞。

(4)礦區在開采時應保證一定坡度比例進行開挖，邊坡適當設置防護網，攔截崩落碎石，并結合實際情況，設置監測設施，保證礦區安全開采。