一種2R1T類(lèi)球面并聯(lián)機(jī)構(gòu)的瞬時(shí)速度分析

張國(guó)英, 劉冠峰, 管貽生

(1.廣東工業(yè)大學(xué) 機(jī)電工程學(xué)院, 廣州 510006； 2.廣東技術(shù)師范大學(xué) 機(jī)電學(xué)院, 廣州 510665)

兩轉(zhuǎn)一移(2R1T)并聯(lián)機(jī)構(gòu)因其自由度少、結(jié)構(gòu)簡(jiǎn)單、制造成本低、適用于多種場(chǎng)合等優(yōu)勢(shì)，已引起國(guó)內(nèi)外學(xué)者的廣泛關(guān)注. 自Hunt[1]于1983年提出一種構(gòu)型為3-RPS并聯(lián)機(jī)構(gòu)以來(lái)，2R1T并聯(lián)機(jī)構(gòu)的構(gòu)型綜合近年來(lái)在國(guó)內(nèi)也掀起一股研究熱潮[2-9]. 這類(lèi)機(jī)構(gòu)目前已成功應(yīng)用于五軸混聯(lián)機(jī)床的轉(zhuǎn)動(dòng)中心[10]、姿態(tài)調(diào)整裝置[11]以及坐標(biāo)測(cè)量機(jī)[12]等.

速度分析是并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)性能分析和動(dòng)力學(xué)分析的基礎(chǔ)，屬于微分運(yùn)動(dòng)的范疇，常用的分析方法有閉環(huán)矢量法、旋量法、影響系數(shù)法[13-14]和網(wǎng)絡(luò)分析法[15]等. 前三種方法實(shí)質(zhì)是求解速度映射即雅克比矩陣，一般通過(guò)對(duì)位置約束方程求導(dǎo)來(lái)獲得速度映射關(guān)系，但在位置約束方程本身就很復(fù)雜的情況下，對(duì)其進(jìn)行一階求導(dǎo)就更加困難. 網(wǎng)絡(luò)分析法以圖論為基礎(chǔ)，適合多環(huán)強(qiáng)耦合并聯(lián)機(jī)構(gòu)的速度和力分析，對(duì)于少自由度并聯(lián)機(jī)構(gòu)的速度分析通用性不強(qiáng).

為避開(kāi)雅克比矩陣和位置導(dǎo)數(shù)的求解，本文在文獻(xiàn)[9]的基礎(chǔ)上，利用Riemann對(duì)稱(chēng)空間理論對(duì)一種自由度類(lèi)球面并聯(lián)機(jī)構(gòu)進(jìn)行了瞬時(shí)速度分析. 從機(jī)構(gòu)子鏈旋量系的對(duì)稱(chēng)性出發(fā)，建立各子鏈關(guān)節(jié)運(yùn)動(dòng)的約束，從而簡(jiǎn)化機(jī)構(gòu)動(dòng)平臺(tái)瞬時(shí)速度的計(jì)算. 根據(jù)計(jì)算和仿真的對(duì)比結(jié)果來(lái)看，角速度誤差控制在-0.004～0.006 rad/s以?xún)?nèi)，線(xiàn)速度誤差控制在-0.01～0.015 mm/s以?xún)?nèi). 采用對(duì)稱(chēng)空間理論方法計(jì)算瞬時(shí)速度用時(shí)5.187 s.

1 機(jī)構(gòu)描述及其坐標(biāo)系建立

機(jī)構(gòu)由等半徑的動(dòng)平臺(tái)和基座以及3個(gè)相同的支鏈組成. 在初始位形下，機(jī)構(gòu)的幾何簡(jiǎn)圖如圖1所示. 3個(gè)支鏈呈120°均勻分布于基座和動(dòng)平臺(tái)之間. 與基座相連的轉(zhuǎn)動(dòng)副記為Bi(i=1,2,3)，它們的軸線(xiàn)相交于基座中心OB，與動(dòng)平臺(tái)相連的轉(zhuǎn)動(dòng)副記為Di(i=1,2,3)，它們的軸線(xiàn)相交于動(dòng)平臺(tái)中心OD；每條支鏈上的球副記為Si(i=1,2,3)，其空間布置為SiOB⊥OBBi,SiOD⊥ODDi,‖SiOD‖=‖SiOB‖. 任意位形下，動(dòng)平臺(tái)和基座關(guān)于3個(gè)球副所組成的平面S1S2S3對(duì)稱(chēng)，動(dòng)平臺(tái)可以繞對(duì)稱(chēng)面內(nèi)的任意直線(xiàn)發(fā)生連續(xù)轉(zhuǎn)動(dòng)，也可以沿兩平臺(tái)中心連線(xiàn)方向進(jìn)行連續(xù)平移.ODS1S2S3OB為一個(gè)六面體，平面S1S2S3將此六面體分為上下對(duì)稱(chēng)的兩部分，OB和OD始終關(guān)于S1,S2,S3組成的平面對(duì)稱(chēng).

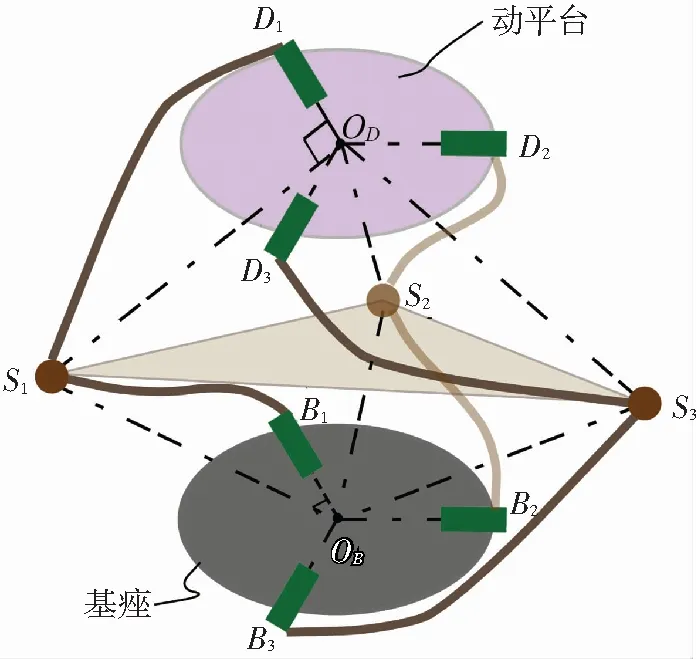
圖1 并聯(lián)機(jī)構(gòu)的幾何簡(jiǎn)圖

建立基坐標(biāo)系OBxyz(記為{FW})和動(dòng)坐標(biāo)系ODuvw(記為{FT})，如圖2所示. 初始位形下，基座與動(dòng)平臺(tái)平行，各轉(zhuǎn)動(dòng)副軸線(xiàn)也相互平行.OBOD⊥S1S2S3交S1S2S3于點(diǎn)M，‖OBM‖=‖ODM‖,‖OBSi‖=‖ODSi‖=l.

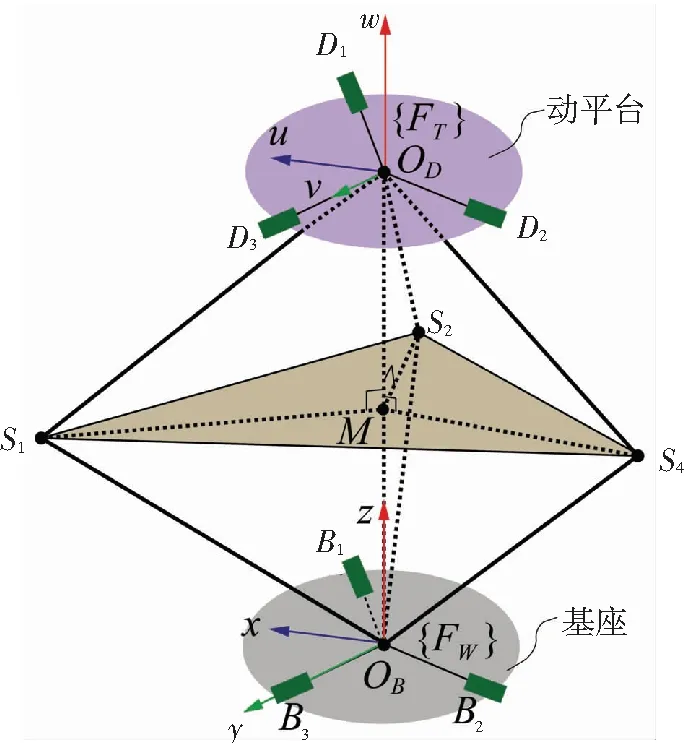
圖2 機(jī)構(gòu)坐標(biāo)系

2 位置正解

在基坐標(biāo)系{FW}中，S1,S2,S3的位置由驅(qū)動(dòng)副Bi的轉(zhuǎn)角αia(i=1,2,3)和l決定，可寫(xiě)為

Si=Ri[-lcαia,0,lsαia]T,

(1)

其中

對(duì)稱(chēng)平面方程ax+by+cz+d=0由各球副的位置坐標(biāo)確定，滿(mǎn)足下式:

(2)

根據(jù)點(diǎn)關(guān)于平面對(duì)稱(chēng)點(diǎn)的求解原理，容易得到動(dòng)平臺(tái)中心OD在{FW}下的位置坐標(biāo)：

(3)

其中，A=a2+b2+c2. 展開(kāi)式(3)即可求得機(jī)構(gòu)的位置正解為

(4)

其中

si表示sinαia，ci表示cosαia，s12表示sin(α1a+α2a)，s13表示sin(α1a+α3a).

3 瞬時(shí)速度分析

3.1 Riemann對(duì)稱(chēng)空間理論

定義1[16]設(shè)p是Riemann流形M中的一點(diǎn)，如果存在M的一個(gè)變換σp：M→M滿(mǎn)足下面3個(gè)條件：

1)σp是對(duì)合的，即σp2=id(id表示恒等變換)但σp≠id；

2)σp是保長(zhǎng)變換(即等距變換)；

3)p是σp的孤立不動(dòng)點(diǎn)，即有p的鄰域U，使得?q∈U,σp(q)=pq-1p.

則稱(chēng)M對(duì)于p成中心對(duì)稱(chēng)，σp叫作關(guān)于p的中心對(duì)稱(chēng).

定義2如果一個(gè)Riemann流形M對(duì)于M中任意一點(diǎn)p，q都成中心對(duì)稱(chēng)，則稱(chēng)M為Riemann對(duì)稱(chēng)空間(簡(jiǎn)稱(chēng)對(duì)稱(chēng)空間).

Riemann對(duì)稱(chēng)空間的2個(gè)典型例子就是歐幾里德空間和球體[17]. 在機(jī)構(gòu)學(xué)中存在一種符合Riemann對(duì)稱(chēng)的并聯(lián)機(jī)構(gòu)，它是一類(lèi)具有對(duì)稱(chēng)幾何結(jié)構(gòu)支鏈的并聯(lián)機(jī)構(gòu). 每條支鏈可分為相連的兩個(gè)子支鏈(C+,C-)，如圖3所示. 它們的運(yùn)動(dòng)副的空間分布滿(mǎn)足一種特殊的對(duì)稱(chēng)，即可以通過(guò)符號(hào)相反的一對(duì)運(yùn)動(dòng){φ,-φ}使得兩個(gè)子鏈重合為一個(gè)子鏈.

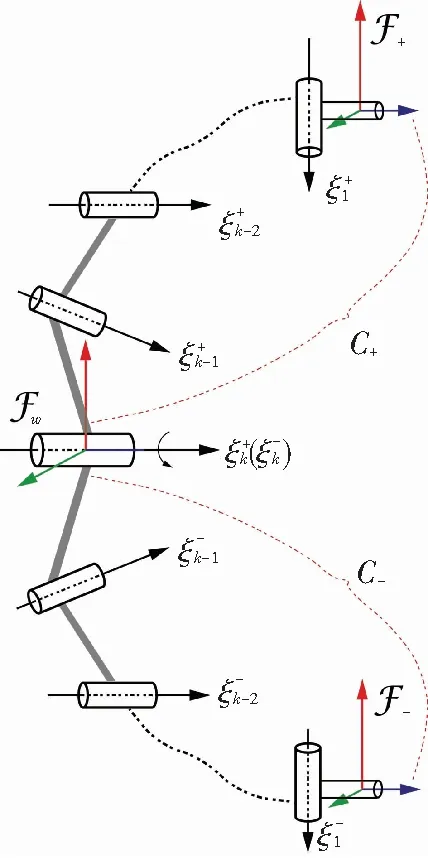
圖3 對(duì)稱(chēng)并聯(lián)機(jī)構(gòu)的子支鏈圖

如果重合子鏈的旋量系為ξk,…,ξ1，則原有支鏈的2個(gè)子支鏈的旋量系為

容易得到子鏈{C++C-}的運(yùn)動(dòng)學(xué)正解為

f(α)=eξ1(α1+φ1)…eξk(αk+φk)eξk(αk+φk)…eξ1(α1+φ1)

如果在剛體運(yùn)動(dòng)群SE(3)上定義一個(gè)反射映射：σp(q)=pq-1p，則上述子鏈的正向運(yùn)動(dòng)學(xué)可以寫(xiě)為

f(α)=σeξ1(α1+φ1)(σeξ2(α2+φ2))(…σeξk(αk+φk)(e)…).

考慮與f像空間對(duì)應(yīng)的SE(3)的子流形Q. 由于f是多個(gè)反射的組合，Q必須是SE(3)的對(duì)稱(chēng)子空間.

定理1如果TeQ=ξk,…,ξ1?SE(3)，則f的像空間包含Q的關(guān)于e的一個(gè)鄰域.

定理2如果并聯(lián)機(jī)構(gòu)的所有支鏈的約束空間的和正好是TeQ的正交補(bǔ)，則并聯(lián)機(jī)構(gòu)的任務(wù)空間包含Q的關(guān)于e的一個(gè)鄰域. 并且每條子鏈的C+，C-轉(zhuǎn)過(guò)的角度正好相反.

本機(jī)構(gòu)任意時(shí)刻的運(yùn)動(dòng)都可以想象為在一個(gè)球體(或橢球體)內(nèi)進(jìn)行. 動(dòng)平臺(tái)與基座始終對(duì)稱(chēng)，對(duì)稱(chēng)面為過(guò)S1,S2,S3的圓面(或橢圓面)，如圖4(a)所示. 由于球副S可以等效3個(gè)轉(zhuǎn)動(dòng)副R串聯(lián)，各等效轉(zhuǎn)動(dòng)副的交點(diǎn)為球副的中心，故將本機(jī)構(gòu)中各支鏈的球副Si(i=1,2,3)局部等效為3個(gè)軸線(xiàn)相交于球副中心的轉(zhuǎn)動(dòng)副R2-,R2+,R3+(R3-)，如圖4(b)所示，R2-的軸線(xiàn)沿SiOB方向，R2+的軸線(xiàn)沿SiOD方向，R3-(R3+)的軸線(xiàn)位于對(duì)稱(chēng)面S1S2S3內(nèi)且與連接兩平臺(tái)的轉(zhuǎn)動(dòng)副軸線(xiàn)同向. 這樣，機(jī)構(gòu)的每條支鏈上下兩部分可以相互折疊后重合，成為在對(duì)稱(chēng)平面里的同一個(gè)RRR結(jié)構(gòu).

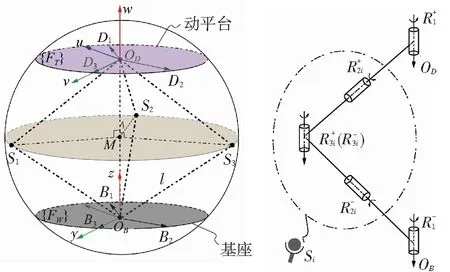
(a) (b)

至此可以得出結(jié)論：本機(jī)構(gòu)是一個(gè)具有Riemann對(duì)稱(chēng)空間性質(zhì)的機(jī)構(gòu)，其每條支鏈經(jīng)過(guò)等效處理后，支鏈的上下2條子鏈也是對(duì)稱(chēng)的，因此，上子鏈與動(dòng)平臺(tái)的夾角和下子鏈與基座的夾角相互為負(fù). 即轉(zhuǎn)動(dòng)副Bi,Di的轉(zhuǎn)角關(guān)系為：αip=-αia(i=1,2,3)，其中αia為平面OBBiSi與基座的夾角，αip為平面ODDiSi與動(dòng)平臺(tái)的夾角. 以B3,D3的轉(zhuǎn)角關(guān)系α3p=-α3a為例，如圖5所示.

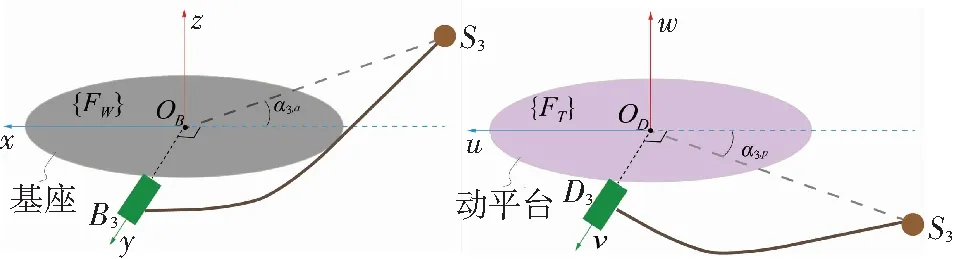
圖5 轉(zhuǎn)動(dòng)副B3, D3的轉(zhuǎn)角

3.2 等效瞬時(shí)速度空間

構(gòu)造運(yùn)動(dòng)旋量ξi(i=1,2,3)與每個(gè)關(guān)節(jié)對(duì)應(yīng)，它表示第i個(gè)關(guān)節(jié)的旋量運(yùn)動(dòng)，此時(shí)除第i個(gè)關(guān)節(jié)外其他所有關(guān)節(jié)均固定于αja=0的位置. 在研究轉(zhuǎn)動(dòng)關(guān)節(jié)時(shí)，其運(yùn)動(dòng)旋量ξi可表示為

(5)

其中，wi∈R3表示旋轉(zhuǎn)軸線(xiàn)上單位矢量，qi∈R3表示軸線(xiàn)上任一點(diǎn). 對(duì)移動(dòng)關(guān)節(jié)有

(6)

下面分別以機(jī)構(gòu)的3種特殊運(yùn)動(dòng)為例，推導(dǎo)其運(yùn)動(dòng)旋量表達(dá)式.

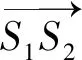
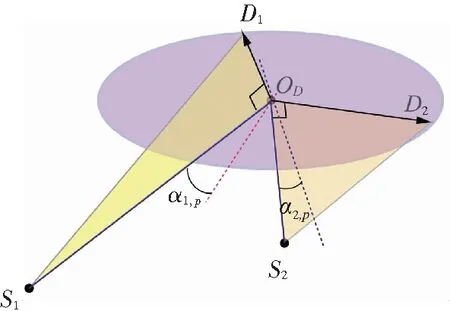
圖6 第一種運(yùn)動(dòng)：固定S1, S2，讓S3自由運(yùn)動(dòng)

Fig.6 Motion pattern Ⅰ: fixS1,S2and freeS3

該運(yùn)動(dòng)情形下的運(yùn)動(dòng)旋量為

(7)

(8)

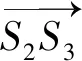
(9)

運(yùn)動(dòng)旋量系{ξ1,ξ2,ξ3}等效為繞對(duì)稱(chēng)面S1S2S3內(nèi)任意一條直線(xiàn)的轉(zhuǎn)動(dòng)(2個(gè)旋轉(zhuǎn)自由度)，以及沿對(duì)稱(chēng)面法線(xiàn)方向的平移(1個(gè)平移自由度)，其維數(shù)等于機(jī)構(gòu)的自由度數(shù)，很好地解釋了類(lèi)球面并聯(lián)機(jī)構(gòu)2R1T的自由度性質(zhì)，物理意義明確.

由于動(dòng)平臺(tái)的運(yùn)動(dòng)是由3個(gè)驅(qū)動(dòng)關(guān)節(jié)共同作用引起，其運(yùn)動(dòng)可以由旋距為零的速度旋量來(lái)描述:

(10)

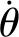
(11)

式中，ξ1,ξ2,ξ3分別為驅(qū)動(dòng)關(guān)節(jié)B1,B2,B3在基坐標(biāo)系下的等效運(yùn)動(dòng)旋量，ξ的集合就構(gòu)成了機(jī)構(gòu)末端在基坐標(biāo)系下的速度空間.

4 計(jì)算與仿真

選取機(jī)構(gòu)主要參數(shù)為：l=100 mm. 不失一般性，令驅(qū)動(dòng)關(guān)節(jié)的角位移分別為

(12)

根據(jù)式(1)～(11)對(duì)動(dòng)平臺(tái)的瞬時(shí)速度(包括角速度和線(xiàn)速度)進(jìn)行ADAMS仿真并與Mathematica計(jì)算結(jié)果進(jìn)行對(duì)比，結(jié)果如圖7所示. 由圖7可知，仿真結(jié)果與理論計(jì)算幾乎完全吻合，說(shuō)明采用對(duì)稱(chēng)空間理論分析機(jī)構(gòu)的瞬時(shí)速度是正確、可行的.

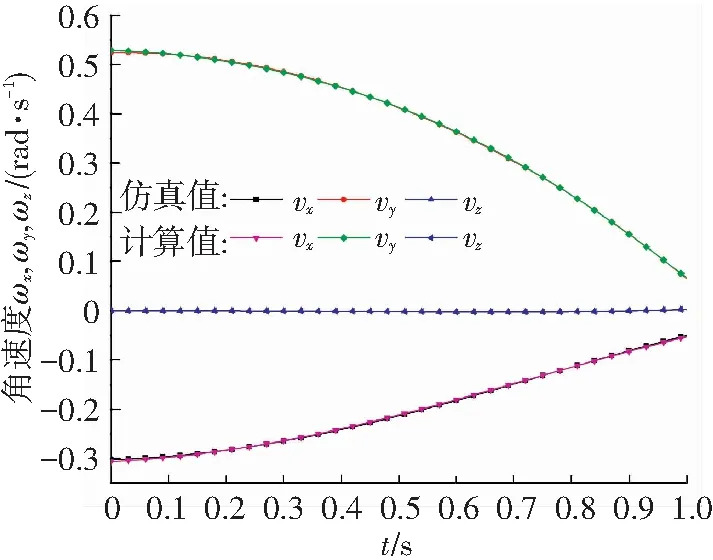
(a)角速度的仿真值與計(jì)算值對(duì)比

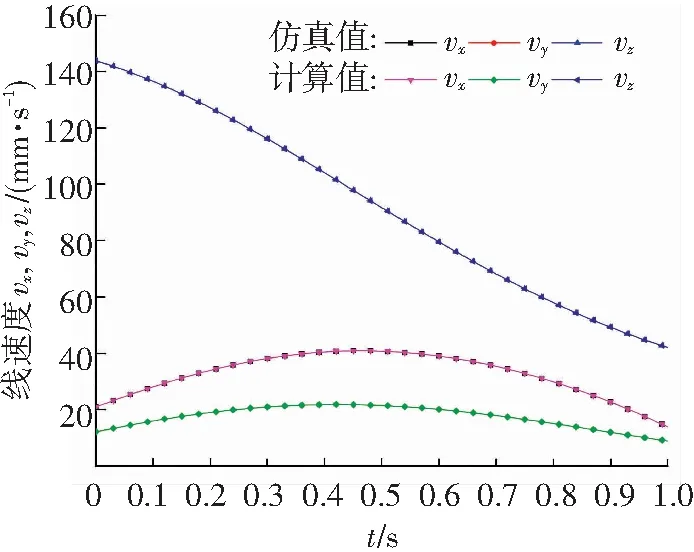
(b)線(xiàn)速度的仿真值與計(jì)算值對(duì)比

Fig.7 Instantaneous velocity computed and simulated by symmetric space theory

5 結(jié) 論

對(duì)一種對(duì)稱(chēng)結(jié)構(gòu)的3自由度類(lèi)球面并聯(lián)機(jī)構(gòu)進(jìn)行了位置分析. 由于位置解析式較為復(fù)雜，若通過(guò)對(duì)其進(jìn)行一階求導(dǎo)或推導(dǎo)其雅克比矩陣的方式來(lái)獲得機(jī)構(gòu)的瞬時(shí)速度將是十分困難的事情. 為簡(jiǎn)化計(jì)算，利用對(duì)稱(chēng)空間理論，從機(jī)構(gòu)子鏈旋量系的對(duì)稱(chēng)性出發(fā)，建立各子鏈關(guān)節(jié)運(yùn)動(dòng)的約束. 由于機(jī)構(gòu)有三個(gè)驅(qū)動(dòng)關(guān)節(jié)，每次鎖定2個(gè)驅(qū)動(dòng)關(guān)節(jié)，只讓1個(gè)關(guān)節(jié)運(yùn)動(dòng)，這樣就可以得到3種特殊的運(yùn)動(dòng)及其運(yùn)動(dòng)旋量，這些運(yùn)動(dòng)旋量和對(duì)應(yīng)的驅(qū)動(dòng)關(guān)節(jié)速度的線(xiàn)性組合構(gòu)成了機(jī)構(gòu)的瞬時(shí)速度空間. 這個(gè)空間的基正好解釋了機(jī)構(gòu)的自由度性質(zhì)為兩旋轉(zhuǎn)一平移，物理意義明確，計(jì)算方法簡(jiǎn)單.