基于稀疏堆疊自編碼器和Circle Loss 的電機故障診斷

王玉龍，于凱，王哲，范尊正，陸慧

（安徽華電宿州發電有限公司，安徽 宿州 234000）

電機在工業生產中起著重要作用，然而，由于其常運行于復雜環境中，極易發生故障，嚴重影響企業的生產。電機故障診斷不僅能提高電機的安全性，同時，也能降低維護成本，對提高企業的整體經濟效益具有重大意義。

傳統的電機故障診斷方法，如K 最近鄰算法、支持向量機（SVM）和人工神經網絡（ANN），其主要步驟為故障特征提取和故障分類，但這些方法高度依賴專家知識，診斷準確性不高。另外，不同工況下電機故障特征也不同，上述方法在恒定轉速下效果良好，但對于可變轉速情況效率則大大降低。

目前，深度學習由于其強大的特征提取能力，能進行無監督的特征學習和分層特征提取，已成為解決計算機視覺和自然語言處理問題的有力工具，其不僅提高了各領域的分類問題的性能，而且還降低了特征提取和選擇過程的復雜性。

本文利用深度學習的數據驅動思想，提出了一種轉速波動下快速高效的電機故障診斷方法。首先，計算輸入轉速加速度信號的頻率特征分布。在此基礎上，將復包絡譜作為稀疏堆疊自編碼器（SSAE）的輸入，并在SSAE 輸出端通過Circle Loss 進行故障分類。為驗證所提診斷方法的泛化能力，設計了最佳的網絡結構，同時，對來自四個不同轉速下故障數據進行了測試。結果表明，所提方法診斷準確性高，復雜度低，對轉速恒定和波動均具有很好的適應性，能夠對轉速波動電機進行有效故障診斷。

1 復包絡譜計算

復包絡譜由實信號經過希爾伯特變換生成，對于時域信號x(t) ，對其進行希爾伯特變換得到解析信號a(t) ，其形式為。

2 稀疏堆疊自編碼器（SSAE）

堆疊自編碼器是由多個自編碼器堆疊而成，其將輸入x(t) 映射到隱空間表示，即：

其中，f1,W,b為編碼器的激活函數、權重和偏置。

解碼器通過從低維空間中重建輸入，即：

式中，f2,W,′b′為解碼器的激活函數、權重和偏置。

但堆疊自編碼器泛化差，不適合轉速波動故障，故本文通過加入稀疏約束，形成SSAE，降低訓過擬合問題，并提高SAE 網絡的泛化性能，網絡的稀疏性通過在SAE 損失函數中引入正則項控制，即：

式中，稀疏正則項由KL 散度定義。

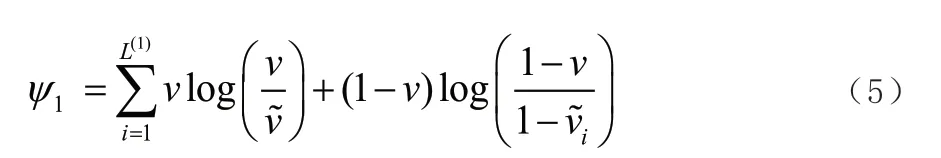
式中，為第i層經過激活函數后的輸出。

3 Circle 損失

深度特征學習通常最大化類內相似度sp和最小化類間相似度sn，但sp和sn上的梯度的值總是一樣的，這降低了特征空間的可分性。故本文把所有的sp和sn兩兩相減得到以下的Circle 損失函數。

定義sp的最優值為Op，sn的最優值為nO，且np O

個相似性得分與最優值偏離較遠，Circle Loss 將分配較大的權重，從而對它進行強烈的優化更新。為此，本文權重調整方式如下。

4 SSAE 網絡訓練流程

綜上所述，SSAE 訓練步驟如下：

（1）采用Xavier 方法初始化網絡權重和偏置；

（2）輸入樣本x，并計算相應的激活值；

（3）計算網絡每層輸出和前饋量；

（4）計算Circle Loss；

（5）通過Circle Loss 反向傳播更新權重；

（6）更新Circle Loss 數的梯度；

（7）重復以上步驟直至網絡收斂。

5 仿真驗證

本節使用宿州電廠電機的故障數據測試所提方法的有效性。分別在電機的外部，內部和轉軸設置不同故障，收集對應的轉速加速度，采樣率為12kHz，故障直徑為0.1778mm，裂紋深度為0.27cm。

設置1722、1748、1772 三種轉速，形成四個數據集，分別包括正常、內圈、外圈和轉軸等468 個故障樣本。使用來自一個轉速數據訓練網絡，其他轉速數據進行驗證。

5.1 SSAE 的網絡結構設計

5.1.1 權重稀疏占比

研究發現，稀疏性保持在0.15 ～0.2 時，重構誤差幾乎不變。因此，本文的稀疏率值為0.15。

5.1.2 隱藏層數

研究對比可知，當SSAE 使用4 個隱藏層時，重構誤差最小。此外，隨著隱藏層數量的增加，重建誤差并無明顯下降。

綜上，本文的網絡結構如表1 所示。

表1 故障診斷網絡結構

5.2 仿真結果

為進一步地說明所提方法故障診斷效果，本文對比振動頻譜成像（VSI）、BP 網絡以及本文方法的診斷精度，其結果如表2 所示。

表2 不同故障診斷方法精度

VSI 方法基于振動頻譜成像和人工神經網絡的軸承故障診斷，首先，對振動信號進行快速傅立葉變換，將頻譜進行疊加創建灰度圖像，經過8×4 大小的濾波器后，利用閾值法轉換為二進制圖像，ANN 的輸入即為該二進制圖像。

從表2 可以看出，本文方法的平均故障分類精度均在90%以上。而VSI 和BP 兩種方法盡管在恒定速度情況具有較好的診斷性能，但在當速度波動后診斷性能明顯下降。可見，本文方法能有效提取故障的復包絡譜和故障特征頻率特征，從而提高了故障診斷精度。

6 結語

本文提出了一種轉速波動下快速高效的電機故障診斷方法。首先，計算得到輸入轉速加速度信號的復包絡，并將其作為SSAE 的輸入，并通過Circle Loss 函數進行故障分類。為驗證所提方法的泛化能力，本文進行了一系列的對比試驗，設計了最佳的網絡結構，同時，對來四個不同轉速下故障數據進行了測試。結果表明，本文所提方法復雜度降低，泛化能力好，對轉速恒定和波動均具有很好的適應性。