一種太赫茲測云雷達高精度譜矩估計方法

張榮政, 肖 建, 沈艷秋, 王海濤, 趙 前

(上海無線電設備研究所,上海201109)

0 引言

云作為地球輻射收支系統的重要調節器,在大氣能量循環、水循環以及地氣系統中扮演著非常重要的角色。太赫茲雷達相比于毫米波雷達對非降水云的觀測具有更高的靈敏度,可用于獲取云內部信息。太赫茲主動云探測技術既能有效彌補當前云遙感手段中冰云探測能力的不足,又有助于提升云相關參量數據反演的精度,對促進天氣預報和氣候預測的研究具有重要意義[1]。

為準確反演云參數,需要精確提取云回波的譜矩信息,即完成對氣象粒子的雷達反射率因子、平均多普勒速度和速度譜寬的估計。目前,國內外新一代脈沖多普勒全相參體制的天氣雷達,常用的譜矩估計方法有基于功率譜密度函數的估計法[2](簡稱傳統譜處理法)以及基于自相關函數的脈沖對處理(Pulse Pair Processing,PPP)法[3-4](簡稱脈沖對處理法),其中傳統譜處理法較為靈活且應用范圍較廣。由于氣象回波信噪比通常很低,需要通過信號積累以及噪聲抑制等手段才能獲得較好的譜矩估計結果。

當前傳統譜處理法在高信噪比條件下的應用效果良好,但是該方法在回波信噪比低且相位噪聲差的太赫茲測云雷達系統中表現稍差,速度和速度譜寬估計精度不高。脈沖對處理法對穩定干擾的抑制效果較差,在早期天氣雷達中應用較為廣泛,本文不再進一步討論。本文利用信號頻域處理的靈活性以及自相關處理對隨機信號良好的抑制特性,提出了一種基于頻域處理的自相關譜矩估計法來提取速度和速度譜寬參數。并通過實驗仿真,驗證該方法在太赫茲測云雷達系統中應用的有效性。

1 譜參數估計方法

基于頻域處理的太赫茲測云雷達自相關譜矩估計法主要包括回波信號相干積累、頻譜處理(如加窗、取模平方等)、譜平均以及速度和速度譜寬估計等步驟,最終獲得云回波的速度和速度譜寬參數。

1.1 相干積累

相干積累主要用于提升氣象雷達的回波信噪比。氣象雷達接收的回波信號中,氣象目標回波信號常常淹沒在噪聲中,單個回波脈沖的信噪比很低。為了提高信噪比,有效提取氣象信息,需要對回波信號進行相干積累。基于回波信號相干的特性,將多個相鄰脈沖的回波信號進行平均和去直流操作,該過程實質是時域平均濾波,且操作簡單。假設太赫茲測云雷達接收到的回波信號x(n)包括氣象目標回波信號s(n)和干擾c(n),可以表示為

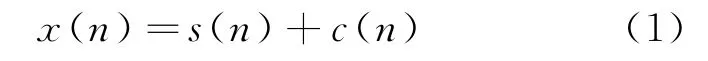
設x(n)的脈沖重復頻率為fp,將回波信號x(n)積累M次得到的信號可表示為

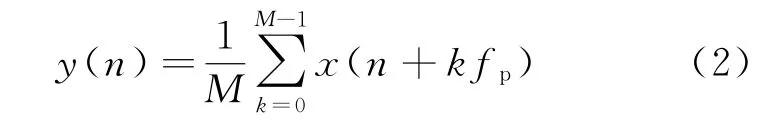
雷達回波中的噪聲和氣象目標回波信號相互獨立,相干積累后的信號可以認為是氣象目標信號和噪聲的各自平均之和,則

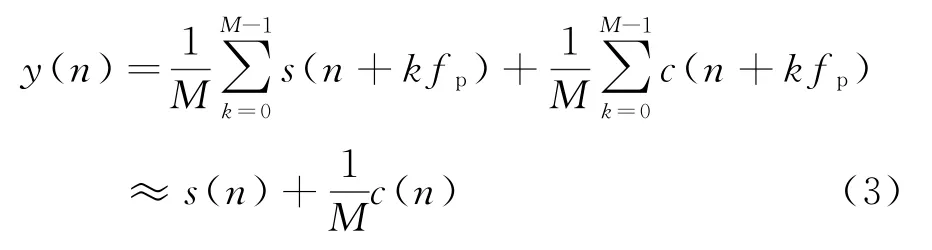
M次相干積累理論上可使回波信噪比提高M倍。實際應用中,由于回波信號相干時間的限制以及速度測量范圍的要求,相干積累的次數通常受限。因此,時域相干積累的次數需要根據實際情況確定。

1.2 頻譜處理

觀測和理論研究表明,大部分氣象回波信號在同一距離門內的功率譜服從高斯分布[5]。考慮到在頻域內處理穩定的雜波和直流信號具有較大的優勢,且當前硬件水平完全滿足傅里葉變換的運算要求,故對相干積累后的回波信號進行加窗、取模平方、雜波抑制和去直流等處理。得到某一距離門內回波信號的功率譜密度函數S(fi),可表示為

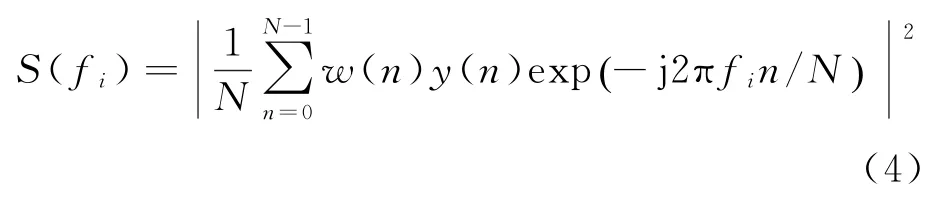
式中:fi為信號頻率;N為總采樣點數;w(n)表示窗函數。S(fi)具有能量密度的意義,反映了信號能量的分布情況。

1.3 譜平均

由于氣象目標存在較強的起伏現象,氣象雷達接收到的信號經過相干積累和單次頻域處理后得到的功率譜具有較強的脈動性。為了減小其脈動,一般采用譜平均的方法來使功率譜變得平穩。所謂譜平均就是將多次譜分析得到的功率譜疊加后求平均值。將功率譜密度S(fi)進行K次平均,平均功率譜可表示為

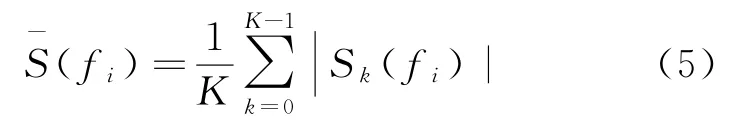
除了減小功率譜的脈動外,譜平均也能夠提高回波信噪比。譜平均處理過程實際是對回波非相參積累處理的過程,進行K次功率譜平均后,回波信噪比理論上可以提升倍。直觀上來看,只要進行足夠次數的譜平均,就可以獲得較高的信噪比。但在實際應用中,譜平均次數受到各種條件的限制,其中最主要的限制包括兩個方面:一是進行譜平均的前提是氣象回波信號多普勒譜的特征保持不變,但實際情況下氣象目標特征的保持時間是有限的,因此譜平均的次數不能是無限的;二是雷達輸出的數據要保持一定的時間分辨率,所以譜平均的時間或次數也會限定在一定范圍內。

1.4 速度和速度譜寬估計

氣象回波信號經過前面步驟處理,可獲得相對穩定的多普勒功率譜密度函數。考慮到氣象回波信號是廣義平穩的確定性信號,符合維納-辛欽定理,因此,對式(5)獲得的平均功率譜進行逆傅里葉變換處理,即可獲得不同時間延遲的自相關函數值。基于自相關函數可估計出云目標的平均速度及速度譜寬,表達式為

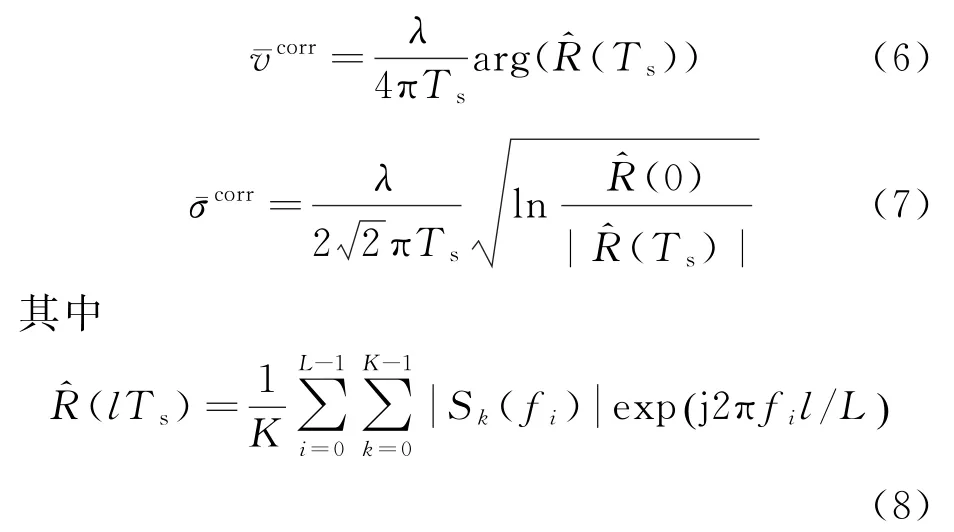
式中:Ts表示發射信號的脈沖重復周期;arg(·)是相位求取函數分別表示回波信號的0階自相關及延遲Ts后的自相關;L表示總采樣點數;l表示脈沖序列間延遲,其中l取0和1時,分別對應。

總之,從回波功率譜函數很容易獲得自相關函數值,且計算量較小。本文提出的方法與傳統譜處理法在運算量上相當。另外,由于譜域平均對雜波和噪聲脈動抑制以及自相關處理對隨機信號的抑制作用,使得該方法相比于傳統譜處理法所估計的速度和速度譜寬參數精度更高。

2 算法仿真

觀測和理論研究表明,大部分氣象回波的功率譜近似服從高斯分布,回波數據模擬分析功率譜可采用高斯分布表征。利用MATLAB軟件對本文提出的基于頻域處理的自相關譜矩估計法進行仿真,同時與天氣雷達廣泛應用的傳統譜處理法的仿真結果進行對比。

太赫茲測云雷達采用線性調頻脈沖壓縮體制,工作頻率為220GHz。具體的仿真參數:波長1.4mm,帶寬12MHz,脈沖重復周期200μs,脈沖寬度2μs,傅里葉變換點數64,譜平均次數8,平均速度0.5m/s,速度譜寬0.2m/s。在信噪比為10dB的情況下,仿真的云回波經過本文方法處理后的功率譜如圖1所示。

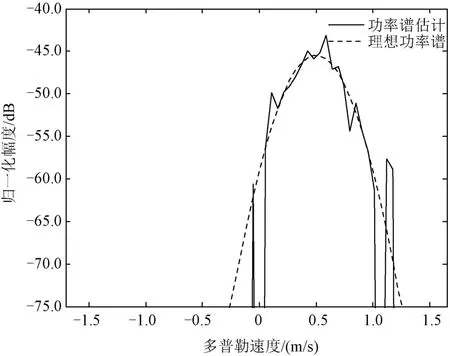
圖1 模擬云回波多普勒功率譜

因氣象回波信號有脈間起伏并存在噪聲,利用本文方法得到的功率譜形狀略有參差,但是基本滿足高斯分布的譜型,且均值和方差也與理想分布一致,增加譜平均次數可令譜線更接近高斯分布。兩種譜矩估計方法計算結果如表1所示。可見,估計結果與仿真輸入參數基本一致。

表1 信噪比10dB時的譜估計結果

為驗證本文方法的可靠性,設置多普勒速度為0.5 m/s,速度譜寬為0.2 m/s,信噪比在(-15～+20)dB之間變化,信噪比變化步進為5dB,對應于每個信噪比均做100次蒙特卡羅仿真實驗。圖2為兩種方法的平均速度和速度譜寬估計蒙特卡羅實驗結果。

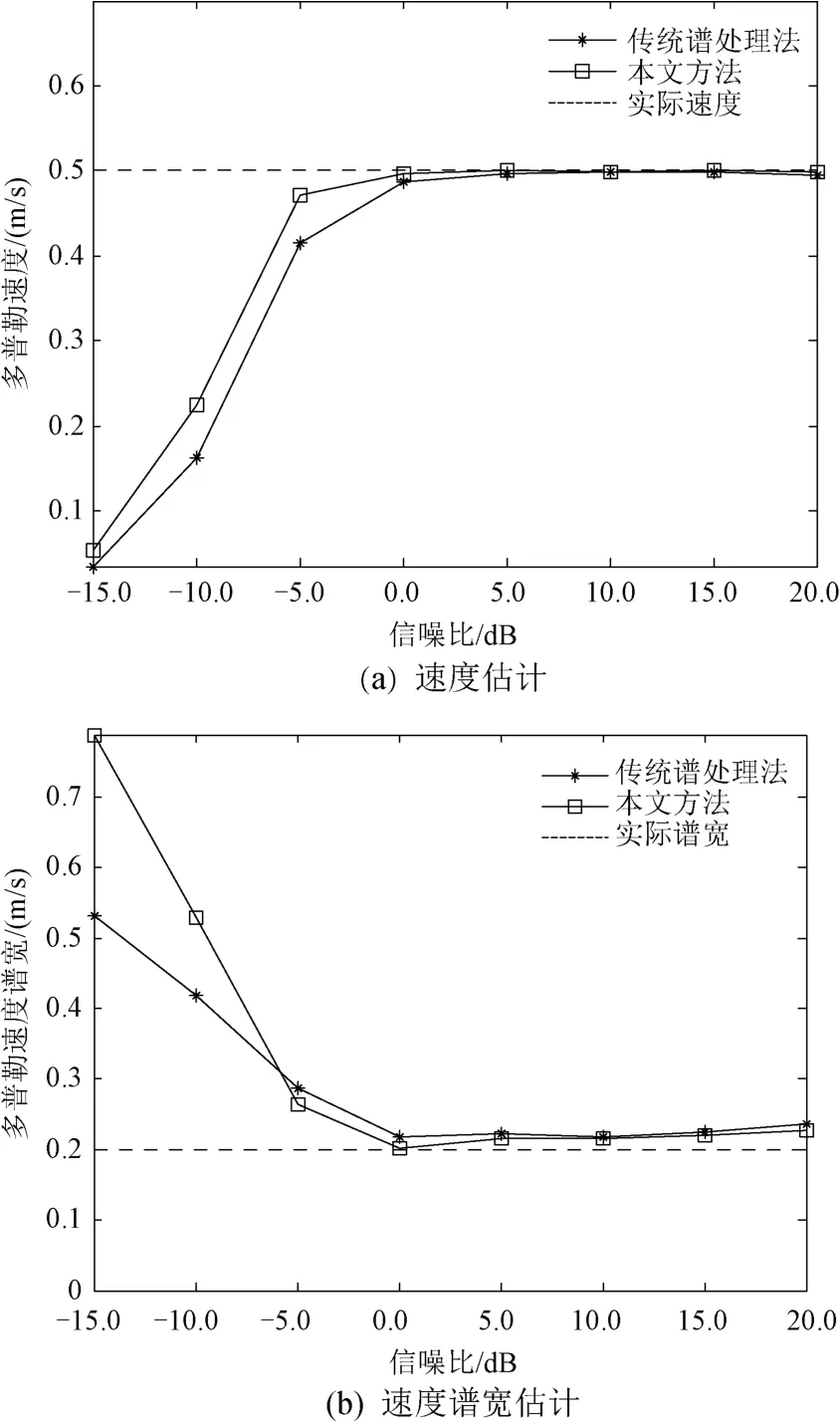
圖2 平均速度和速度譜寬的蒙特卡羅仿真結果

從圖2(a)可以看出:在信噪比大于5dB的高信噪比的條件下,傳統譜處理法和本文所提的方法均能精確估計平均速度;當信噪比為(-5～+5)dB時,本文所提的方法平均速度估計結果精度仍較高,而傳統譜處理法估計得到的平均速度隨信噪比的降低,與真實值的偏差逐漸增大;信噪比小于-5dB時,兩種方法估計性能均惡化嚴重。由圖2(b)可以看出:兩種方法的速度譜寬估計結果都略微大于真實值,但是誤差在信噪比大于5dB時都能保持穩定,滿足估計的要求;隨著信噪比下降,當信噪比小于-5dB時,估計值逐漸偏離真實值。

根據圖2的仿真結果,可以發現無論是平均速度估計還是速度譜寬估計,利用本文所提的方法性能均優于傳統譜處理法,且兩種方法的運算量相當。因此,在設計太赫茲測云雷達系統時,可優先選取本文所提的方法。

3 結論

針對現有云目標速度和譜寬參數估計方法對噪聲抑制效果差,而造成估計精度降低問題,本文在頻域處理的基礎上,結合自相關譜矩估計,提出了基于頻域處理的自相關譜矩估計法。利用MATLAB軟件仿真了整個處理流程,并選取傳統譜處理法作為比較對象,以驗證本文所提的方法的有效性。結果表明,基于頻域處理的自相關譜矩估計法的速度和速度譜寬估計精度均優于傳統譜處理法,可用于太赫茲測云雷達中。