淺析復(fù)核基樁基礎(chǔ)沉降計(jì)算分析研究

姚學(xué)朝 江蘇省有色金屬華東地質(zhì)勘查局

一、引言

樁基礎(chǔ)作為一種歷史悠久的基礎(chǔ)形式，應(yīng)用非常廣泛。樁基設(shè)計(jì)理論，主要是考慮承載力是否滿足要求，也即設(shè)計(jì)時(shí)樁承擔(dān)絕大部分荷載，如果按照傳統(tǒng)的樁基理論來(lái)設(shè)計(jì)，必然會(huì)造成用樁總數(shù)過(guò)多、工程造價(jià)過(guò)高，差異沉降滿足設(shè)計(jì)要求而總沉降卻遠(yuǎn)低于允許沉降量。

因此復(fù)合樁基差異沉降控制優(yōu)化設(shè)計(jì)方法出現(xiàn)了，它能利用樁間土承載能力，在滿足整體承載力的要求下，可以降低和控制建筑物的沉降。復(fù)合基樁由單樁及其對(duì)應(yīng)面積的承臺(tái)底地基土共同組成，傳力路徑為上部荷載-承臺(tái)-樁-樁間土，一方面發(fā)揮樁基的優(yōu)勢(shì)，減少建筑物沉降；另一方面讓樁土協(xié)同作用，滿足承載力要求，此項(xiàng)設(shè)計(jì)理念，經(jīng)濟(jì)上合理，技術(shù)上先進(jìn)。

二、復(fù)合樁基差異沉降計(jì)算模型

（一）土體的本構(gòu)模型

土體采用摩爾～庫(kù)侖理想彈塑性模型，是較為理想的本構(gòu)模型。摩爾～庫(kù)侖強(qiáng)度理論對(duì)土的破壞形式做了理想化假定，一般為剪切強(qiáng)度，它與土的粘聚力和法向應(yīng)力有關(guān)，某點(diǎn)在任一平面上剪應(yīng)力達(dá)到此值時(shí)，該點(diǎn)處于極限平衡狀態(tài)，土就發(fā)生破壞。

摩爾～庫(kù)侖模型計(jì)算參數(shù)共7 個(gè)，其中土容重γ、滲透系數(shù)k、凝聚力c、內(nèi)摩擦角φ 可根據(jù)現(xiàn)場(chǎng)實(shí)測(cè)資料來(lái)確定它們的值。

楊氏模量E：Plaxis 計(jì)算程序使用變形模量E，也可根據(jù)壓縮模量Es計(jì)算E 進(jìn)行使用：

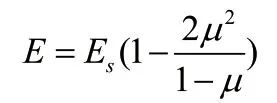
泊松比μ：一般在0.3～0.4 之間，飽和黏土在不排水條件下可能接近0.5。

庫(kù)侖剪切破壞準(zhǔn)則：

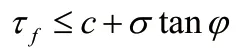
式中，

c 為黏聚強(qiáng)度

φ 為內(nèi)摩擦角

τf為破裂面上的剪應(yīng)力，也是土的抗剪強(qiáng)度

σ 為破裂面上的法向總應(yīng)力。

（二）樁和承臺(tái)的本構(gòu)模型

由于相對(duì)土層來(lái)說(shuō)，樁和承臺(tái)的剛度大，在正常受力條件下，它們一般處于彈性狀態(tài)，故假定它為線彈性，線彈性理論模型，在混凝土受力的應(yīng)力和變形關(guān)系中，屬于簡(jiǎn)單本構(gòu)模型，服從廣義胡克定律，兩個(gè)彈性系數(shù)為E 和μ。表達(dá)式形式如下：

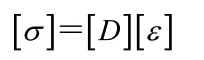
式中，[D]為應(yīng)力應(yīng)變關(guān)系矩陣，表達(dá)式為：

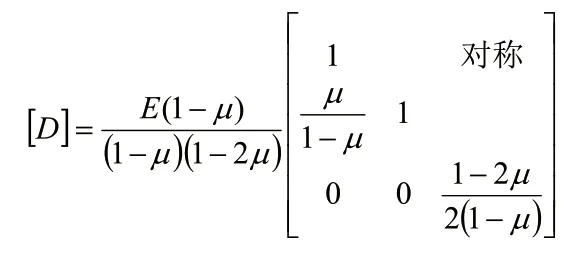
式中，E、μ 分別為彈性系數(shù)。

三、復(fù)合樁基差異沉降計(jì)算思路

根據(jù)多年的研究和經(jīng)驗(yàn)，可以按照以下思路進(jìn)行計(jì)算：①上部結(jié)構(gòu)對(duì)提高建筑物抗彎剛度非常重要，在降低不均勻沉降方面發(fā)揮有限。上部結(jié)構(gòu)中，其剛度矩陣元素存在特有性質(zhì)，因此可以將上部結(jié)構(gòu)的剛度貢獻(xiàn)簡(jiǎn)化到筏板上進(jìn)行考慮。②在保證樁土共同作用的基礎(chǔ)上實(shí)現(xiàn)變剛度的調(diào)平設(shè)計(jì)，因此建筑物的沉降將會(huì)大于按常規(guī)樁基設(shè)計(jì)時(shí)的沉降，土體已經(jīng)工作于非線性狀態(tài)。③由于只進(jìn)行平面分析，將筏板和樁的支承剛度進(jìn)行換算，使板帶的剛度等于筏板的剛度。這樣沿板帶方向計(jì)算出的建筑物不均勻沉降基本反映了建筑物沿該方向的實(shí)際變形特性。

四、實(shí)例計(jì)算

（一）材料參數(shù)

樁型采用預(yù)制樁，砼強(qiáng)度為C30，樁長(zhǎng)30m，樁徑為Φ500。計(jì)算模型的地下水位取為0m，采用二維軸對(duì)稱模型來(lái)分析，樁與承臺(tái)簡(jiǎn)化為線彈性模型，土層簡(jiǎn)化為摩爾－庫(kù)侖模型，粘聚力為1kpa，內(nèi)摩擦角為30 度，泊松比為0.35，荷載按照150kN考慮。

（二）布樁方式

模型1 的布樁方式為：樁數(shù)為7 根，均勻布樁，樁間距3.0m；模型2 的布樁方式為：樁數(shù)為7 根，中間樁距2.5m，邊樁樁距3.0m；模型3 的布樁方式為：樁數(shù)為5根，均勻布樁，樁間距2.5m。

（三）土層指標(biāo)

擬試驗(yàn)場(chǎng)地土層共分為7 層：

②-1 層含水量為39.7%，重度為18.2 kN/m3，孔隙比為1.089，塑性指數(shù)為18.6，液性指數(shù)為0.79，壓縮系數(shù)為0.569 Mpa-1，壓縮模量為3.68Mpa，粘聚力為18kpa，內(nèi)摩擦角為14.3 度。

②-2 層含水量為41.4%，重度為17.7 kN/m3，孔隙比為1.172，塑性指數(shù)為15.9，液性指數(shù)為1.27，壓縮系數(shù)為0.737Mpa-1，壓縮模量為2.99Mpa，粘聚力為16.2kpa，內(nèi)摩擦角為16.6 度。

②-3 層 含 水 量 為25.2%， 重 度 為19.5kN/m3，孔隙比為0.742，塑性指數(shù)為9.27，液性指數(shù)為1.01，壓縮系數(shù)為0.192Mpa-1，壓縮模量為10.36Mpa，粘聚力為13.3kpa，內(nèi)摩擦角為30.0 度。

②-4 層含水量為35.4%，重度為18.0 kN/m3，孔隙比為1.041，塑性指數(shù)為13.9，液性指數(shù)為1.16，壓縮系數(shù)為0.578Mpa-1，壓縮模量為3.56Mpa，粘聚力為15.1kpa，內(nèi)摩擦角為20.9 度。

③-1 層含水量為24.0%，重度為19.4 kN/m3，孔隙比為0.726，壓縮系數(shù)為0.135 Mpa-1，壓縮模量為13.44Mpa，粘聚力為11.9kpa，內(nèi)摩擦角為33.4 度。

③-2 層含水量為23.7%，重度為19.6 kN/m3，孔隙比為0.698，壓縮系數(shù)為0.128 Mpa-1，壓縮模量為14.07Mpa，粘聚力為9.04kpa，內(nèi)摩擦角為33.6 度。

（四）計(jì)算結(jié)果分析

本算例針對(duì)變樁距模型進(jìn)行了對(duì)比分析，模型1 計(jì)算總沉降為94.630mm，差異沉降為6.316mm；模型2 計(jì)算總沉降為91.410mm，差異沉降為13.452mm；模型3 計(jì)算總沉降為113.100mm，差異沉降為13.022mm；

五、結(jié)論與建議

建筑物的平均沉降約為90mm，與計(jì)算結(jié)果比較吻合，按照變剛度調(diào)平的理論方法可以進(jìn)一步的調(diào)平，樁數(shù)尚可進(jìn)一步減少，但是為了滿足建筑物的建筑與構(gòu)造布置，在局部區(qū)域樁數(shù)不能減少。當(dāng)然上述區(qū)域可以通過(guò)縮短樁長(zhǎng)的方法來(lái)減少樁基的卸荷量，從而達(dá)到真正的零差異沉降。