電動汽車動力屏蔽線的表面轉移阻抗仿真與分析

趙鶴鳴，賈 晉，吳小珊，龍 云，安素芹

（1.重慶理工大學車輛工程學院，重慶 400054；2.重慶大學汽車工程學院，重慶 401331；3.重慶清研理工電子技術有限公司，重慶 401329）

屏蔽效能差的動力屏蔽線纜通常會導致電動汽車整車電磁場發射水平超標，無法通過GB/T 18387標準測試（0.15～30 MHz）。目前我國還沒有制定出關于測試電動汽車動力線纜屏蔽效能的標準。如何有效地評估與測試動力線纜的屏蔽效能是線纜供應商以及整車廠關注的工程難題，可以通過仿真途徑進行研究。現在電動汽車上的高壓動力線纜通常采用的是雙層屏蔽，所謂雙層屏蔽是指內屏蔽層采用鍍錫銅絲編織層，外屏蔽層采用鋁塑復合帶（鋁箔）包裹。國外的學者Vance、Tyni、Demoulin等根據電磁場理論，對單層編織線纜模型進行了轉移阻抗值的公式推導，可以有效地仿真對應參數的單層編織線纜的轉移阻抗值。然而這些經典的解析式并未考慮到雙層屏蔽對結果的影響，基于此，本研究通過設置合理的參數提出優化模型。

1 表面轉移阻抗

表面轉移阻抗［2］是表征動力線纜屏蔽性能的特征參數，轉移阻抗越低證明線纜的屏蔽性能越好，其電磁抗擾能力越強。其定義為單位長度的線纜中有電流流過屏蔽層時在芯線和屏蔽層間形成的感應電壓（如圖1所示），即編織層上軸向電壓變化率與軸向電流之比，其計算公式可以表達為

式中：I0表示編織層外表面流過的電流；表示芯線與屏蔽層所組成的均勻傳輸線單位長度上的電壓有效值；z表示線纜軸向方向；圖1中的l表示線纜長度。

2 轉移阻抗解析式

通常電動汽車上采用的高壓動力線纜屬于編織型屏蔽線纜（如圖2所示），因此可以通過線纜編織層的結構參數和電磁場理論來建立轉移阻抗的解析式模型。本節中主要介紹適用于單層屏蔽的Vance、Tyni、Demoulin 3種編織型屏蔽線纜解析式模型，并通過對比得出Demoulin模型計算精度更高，故選用該單層屏蔽模型。接著，進行轉移阻抗特性曲線分析，根據頻率范圍把轉移阻抗曲線劃分4個區域，提出每個區域的主要影響成分。在此基礎上，發現雙層屏蔽線纜中鋁箔對直流電阻和小孔電感項的影響，最終提出了雙層屏蔽線纜的優化模型。

解析法可以有效分析屏蔽線纜參數化對轉移阻抗的影響。關于解析式模型的輸入參數，可以通過7個參數來描述線纜編織層的結構特性：編織層內直徑D0；每根編織線的直徑d；編織層上一圈包含的編織束股數C；每股編織束中的導線根數N；編織角度α；編織層的電導率σ；編織層的磁導率μ。獲得這些參數后就可以對屏蔽線纜的轉移阻抗值進行仿真，編織層的結構參數如圖3所示。

2.1 經典單層屏蔽模型

2.1.1 Vance模型

Vance深入研究了輻射到線纜編織層上時的低頻特性，其編織層轉移阻抗的解析模型（式（2））包含2部分，一部分（Zd）表示通過金屬編織層的電磁波的擴散，另一部分（jωLh1）表示通過編織層的磁場的泄漏。

式中：Zd表示散射阻抗；Lh1表示小孔電感，其中散射阻抗受金屬編織層的直流電阻和電磁波通過圓柱形編織層壁的擴散共同影響。Vance E F等［3］提出了目前應用最廣的散射阻抗Zd表達式：

式中：R0表示單位長度的直流電阻；δ表示集膚深度；m表示菱形孔的極化率；DM=D0+2d表示編織層外直徑。

2.1.2 Tyni模型

Vance模型只提出了散射阻抗和小孔電感，沒有考慮編織電感，所以僅適合于計算編織層投影覆蓋率低的線纜。Tyni改進了Vance小孔電感的表達式（見式（8）），并引入了編織電感部分Lb1（見式（11）），使其在計算高和低投影覆蓋率電纜轉移阻抗時的精度優于Vance耦合理論。編織電感是由于編織層的編織結構導致內部編織層和外部編織層之間的磁通鏈引起的［4］。在α＞45°時為正；在α＜45°時為負，取負號是因為此時編織帶上電流產生的磁場與原磁場方向相反；若α=45°，則由于編織層的編織特性引起的電感為零。當α＜45°，可以使用以下簡化模型：

式中：b表示相鄰編織束之間的距離；h表示2個相交叉編織束之間的距離

2.1.3 Demoulin模型

Demoulin在現有研究的基礎上提出式（12）的解析模型，進一步考慮了額外波動效應［5］。額外波動效應是在高頻情況下，編織網內、外層編織束間的磁場引起的渦旋電流效應，從而產生額外的衰減，導致在高頻范圍內的轉移阻抗值有所減小，該分量可以通過屏蔽層上的切向電場引起的渦流來描述，成正比。

式中：

2.1.4 單層屏蔽模型的對比驗證

文獻［6-7］中給出的3組線纜樣品參數，如表1所示，其中3組線纜的編織層內直徑D0均為2.95 mm，編織線的直徑d均為0.15 mm。

表1 編織線纜樣品參數

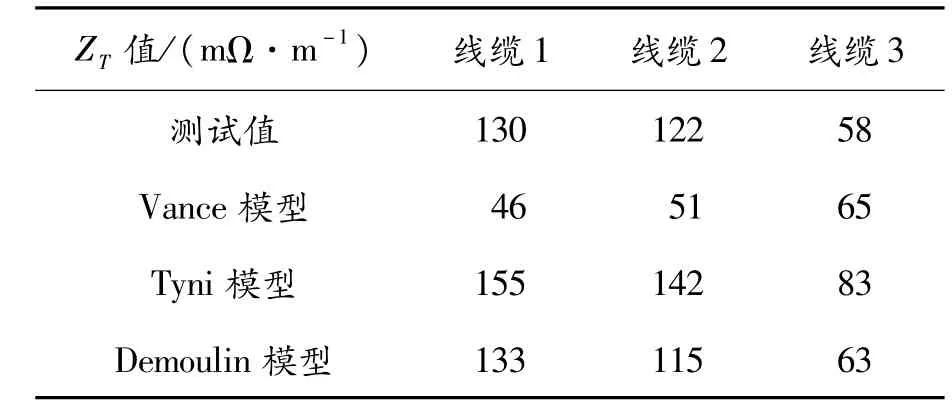
表2 在10 MHz時ZT的測量值與各模型計算值

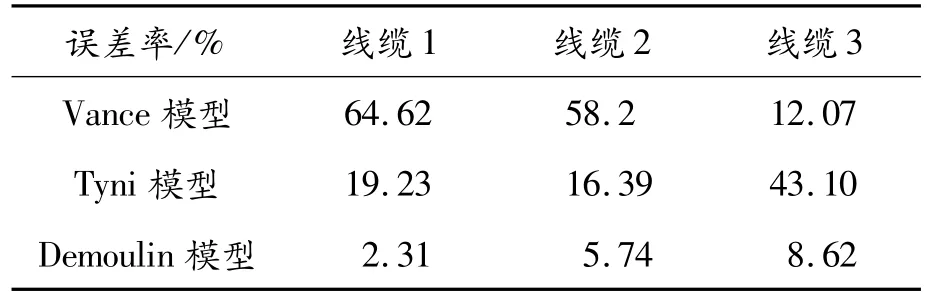
表3 在10 MHz時各模型的計算誤差率

將上述線纜結構參數作為輸入條件，使用各模型進行仿真計算并與測試值做比較。通過表2可知：在10 MHz時，3種單層屏蔽模型中Demoulin模型的ZT計算值更加接近實際測試值［8-10］。從表3可知：Demoulin模型的計算誤差率是最低的，擬合效果較好。線纜1的誤差率為2.31%，線纜2的誤差率為5.74%，線纜3的誤差率為8.62%。所以最終選擇Demoulin模型進行雙層屏蔽優化模型的分析。

2.2 轉移阻抗特征曲線分析

對于動力屏蔽線纜，可以通過RLC電參數來搭建等效電路，如圖4所示，其中電感參數L主要由芯線導體的電感Lc、屏蔽層的電感Ls和兩者之間的互感Mcs組成，除此之外，編織層上還要考慮小孔電感和編織電感Lh&b的影響。電阻參數R主要由內部導體的電阻Rc和屏蔽層的電阻Rs組成，電阻受集膚效應影響隨頻率變化，集膚效應會影響線纜的屏蔽效能和諧振頻率處的阻抗值。電容參數C由芯線和屏蔽層之間的電容Ccs組成。對于轉移阻抗值主要是由感性耦合對其產生影響，所以要關注這些電參數對動力線纜轉移阻抗的影響［11］。

對屏蔽線纜轉移阻抗模型ZT曲線的構成進行分析，如圖5所示。圖中的虛線為影響轉移阻抗值的幾項關鍵分量，分別有Zd、jωL和k，圖中實線為包含各個分量的轉移阻抗曲線。

在區域1（灰色）內，小于150 kHz低頻情況下，編織屏蔽層中的電流密度均勻分布，轉移阻抗值與屏蔽層的直流電阻值R大致相同。在區域2（綠色）內，轉移阻抗主要由散射阻抗Zd決定。這是因為隨著頻率的增加，屏蔽層中的電流密度變得不均勻，由于集膚效應，集膚深度按頻率的平方根減小，ZT值減小。在區域3（黃色）內1 MHz附近，轉移阻抗值由散射阻抗 Zd、小孔電感 jωLh、編織電感 jωLb和額外波動衰減共同決定，產生明顯的拐點現象，這是因為隨著頻率的進一步增加，編織層上的菱形孔導致的磁場泄漏程度加強，小孔電感成分增加。而編織層中兩兩相交的編織束編進、編出會引起磁通量的切割，也產生感應電動勢，形成編織電感，從而轉移阻抗值增加。在高頻情況下，編織網內、外層編織束間的磁場會引起渦流效應，又會產生額外的衰減。在區域4（紅色）內大于2 MHz，主要由小孔電感和編織電感決定，隨著頻率的不斷增加轉移阻抗值不斷變大［12］。

2.3 雙層屏蔽優化模型

在區域1（灰色）小于150 kHz的情況下，轉移阻抗主要由直流電阻決定。而目前電動汽車上的高壓動力線纜通常采用雙層屏蔽，屏蔽層除了內層的鍍錫銅絲編織網，外層還包裹了一層鋁塑復合帶（鋁箔），所以對于被測動力線纜還需考慮在低頻時鋁箔的直流電阻對轉移阻抗值的影響。

由于雙層屏蔽線纜在屏蔽層外側附加了一層鋁箔，與單層屏蔽相比，內側的菱形孔被鋁箔遮蓋，可以有效地避免磁場通過小孔發生泄漏，此時小孔電感效應大大降低，可以忽略不計（圖6）。故會對圖5中區域4（紅色）的高頻部分的小孔電感項產生影響，轉移阻抗值理論上會減小。

綜上分析，針對雙層屏蔽動力線纜提出線纜解析式的優化模型，該優化模型是在Demoulin線纜模型的基礎上，附加鋁箔的直流電阻和消除小孔電感項2個方面因素對轉移阻抗值的影響。

式中RAl表示鋁箔每米的直流電阻值。

對于鋁箔附加的直流電阻值可以通過Q3D軟件建立鋁箔層模型進行數值分析計算提取電阻值。如圖7所示，假設該鋁箔模型為理想狀態具有均勻的厚度，厚度設為0.1 mm，可以任取其中一截進行計算，為了減小計算量長度設為100 mm，通過計算得到被測線纜中的鋁箔的直流電阻0.005Ω/m。

圖8 為輸入相同線纜結構參數的單層屏蔽模型與雙層屏蔽優化模型的仿真結果。從圖中可以看出：優化模型的低頻直流電阻部分的轉移阻抗值有所增大，而高頻電感部分的轉移阻抗值大大降低。說明包裹鋁箔的雙層屏蔽線纜可以有效地提高高頻段的線纜屏蔽效能［13-14］，電動汽車上的高壓動力線纜采用雙層屏蔽其抗外部電磁干擾能力更優。

3 三同軸法測試與對比驗證

3.1 三同軸法測試

三同軸法是把被測線纜放置于同軸的無鐵磁性的良導體管中進行測量的方法，即線纜芯線內導體、線纜屏蔽層和同軸的良導體管三者構成的測試裝置。三同軸法可以將復雜的電磁耦合機理用直接測量的電路參數來表征（將影響屏蔽效能的電磁場用表面電流和表面電荷等效代替），適合非對稱線纜以及不同尺寸和結構復雜連接器測試，測試結果可重復性好。主要有2種路徑連接方式：①由近端芯線注入信號，遠端測試管處接收耦合信號，A、B方法采用該方式；② 由遠端測試管注入信號，芯線處接收耦合信號，C方法采用該方式［15］。

考慮測試穩定性和易操作性，本次測試采用三同軸B方法，參考測試標準：IEC62153-4-3-2013［16］。具體測試用設備見圖9，測試流程見圖10。圖11為三同軸B方法測試原理示意圖。

三同軸B方法轉移阻抗值計算公式為

式中：ameas=20log10（S21）表示測量的衰減損耗；acal表示校準時測量的復合損耗；Z0表示信號發生器和接收機的阻抗，通常為50Ω；Lc表示被測線纜耦合長度；R1表示終端阻抗。

本研究選用的測試樣品為電動汽車雙層屏蔽動力線纜，基本結構參數如下：編織層內直徑D0為10.3 mm，編織線的直徑d為0.15 mm、編織束股數C為24、每股編織束中的導線根數N為8。

3.2 對比驗證

測試中線纜樣品的耦合長度為0.5 m，采用三同軸B方法時其測試截止頻率為50 MHz（最大可測到50 MHz）。如圖12所示，圖中樣品線纜的測試值在50 MHz時產生諧振點，轉移阻抗曲線趨勢發生變化。通過對比雙層屏蔽優化模型的仿真值和樣品線纜實際測試值可知：該仿真有很好的擬合效果。

通過表4數據可以看出：在去除小孔電感和考慮加入鋁箔直流電阻后，優化模型在各頻點的仿真計算值與實際測試值很接近。

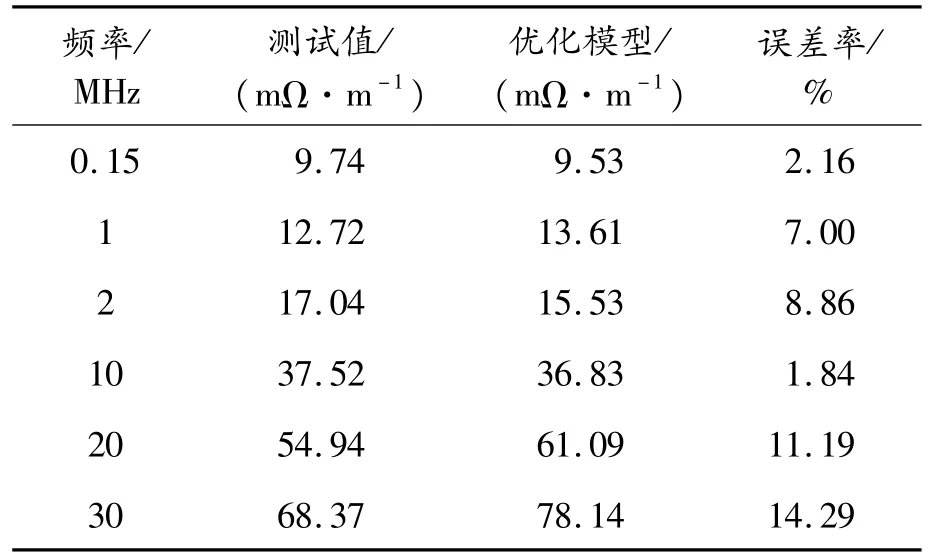
表4 優化模型與樣品測試值

在150 kHz和10 MHz頻點時，誤差率分別為2.16%和1.84%，低于3%；在1 MHz和2 MHz頻點時，誤差率分別為7.00%和8.86%，低于9%；在20 MHz和30 MHz時，誤差率分別為11.19%和14.29%，低于15%（參考大眾標準要求，主要考慮屏蔽線纜在2 MHz和30 MHz時的轉移阻抗值），由此驗證了該雙層屏蔽優化模型的正確性。

4 結論

1）詳細論述了3種經典的編織型單層屏蔽線纜的表面轉移阻抗解析式，對比分析后可知Demoulin模型有更高的計算精度。

2）附加鋁箔的雙層屏蔽線纜與單層屏蔽線纜相比，直流電阻和小孔電感項均有變化。

3）基于Demoulin模型進一步提出了雙層屏蔽動力線纜的優化模型。

4）采用三同軸B方法對樣品線纜進行表面轉移阻抗的測試，經過仿真值與測試值的對比，其有很好的擬合效果，驗證了該雙層屏蔽優化模型的正確性。該研究可為電動汽車動力屏蔽線纜計算表面轉移阻抗的仿真模型改進提供參考。