沖擊載荷下點蝕損傷對30Cr MnSiNi2A鋼應力集中影響的數值模擬研究

陳躍良，張柱柱，張 勇，卞貴學，黃海亮，李軍亮，張楊廣，吳省均

（1.海軍航空大學，山東 青島 266041；2.海軍航空大學航空保障專業兵訓練基地，山東青島 266041）

航母艦載機在起降過程中，由于彈射攔阻等沖擊載荷的作用，使艦載機機體尤其是發動機、起落架、攔阻鉤等部位經受了嚴重的沖擊載荷。同時，艦載機在海洋環境下服役，由于航母的運動、復雜海況等引起的海水浪花飛濺，使甲板上空始終處于潮濕狀態，艦載機不僅受到海上空氣、海水及持續的干/濕交替循環的侵蝕，還會受到艦艇燃燒廢氣、艦載機發動機廢氣等的腐蝕，特別是廢氣與海洋鹽霧組合成pH值達到2.4～4.0范圍的高酸性潮濕液膜，使其受到的環境腐蝕問題尤其嚴峻［1］。沖擊載荷易使結構在腐蝕缺陷處產生損傷，腐蝕也會使損傷發生進一步的擴展。在沖擊載荷與環境腐蝕共同作用下，結構的壽命銳減，給艦載機帶來嚴重安全隱患。沖擊載荷不同于一般的應力載荷加載，其對材料結構造成的損傷機理也不相同，因此有必要對材料在沖擊載荷與環境腐蝕共同作用下的動態力學響應進行研究。

目前國內外學者對腐蝕和應力的共同作用進行了廣泛研究，但主要集中在應力腐蝕［2-4］和疲勞腐蝕［5-7］方面。對于金屬材料的應力腐蝕，不少學者將腐蝕坑等效為規則形狀的缺陷并進行了數值模擬研究。郁大照等［8］研究了腐蝕和多處損傷（multiple site damage，MSD）對飛機結構的影響，建立了含MSD寬板結構的裂紋擴展和剩余強度預測模型。秦廣沖等［9］研究了腐蝕坑對鋼材應力集中和疲勞損傷的影響。梁瑞等［10］對蝕坑對圓棒的應力集中影響進行了研究，并擬合得到了應力集中系數與腐蝕坑深徑比的計算公式。張強等［11］利用有限元軟件建立了圓環鏈腐蝕模型，對溫度與腐蝕面積對圓環鏈的沖擊特性進行了分析研究，得到了不同沖擊特性與溫度及腐蝕面積的關系函數。Patrick等［12］通過數值計算方法研究了微觀結構對腐蝕坑周圍應力分布的影響。Ji等［13］對埋管中腐蝕坑導致的應力集中進行了分析，采用有限元分析方法計算了獨立橢圓形腐蝕坑的應力集中因子，并建立了埋管橢圓形腐蝕統計預測模型。Muhammet等［14］系統研究了球形壓力容器內壓下半橢圓腐蝕坑和半橢圓基坑底部成核的次生坑的應力集中，認為應力集中（stress concentration factor，SCF）發生在半橢圓形凹坑的底部，并隨著凹坑深度的增加而增加，但隨著凹坑寬度的增加而減小，坑深寬比是影響應力的主要參數，基坑底部的次生坑凹坑會加劇應力分布和SCF。

目前對于金屬材料在沖擊和腐蝕共同作用下的力學性能研究主要集中在沖擊載荷對材料耐蝕性的影響，對于腐蝕材料的動態力學響應研究還較少。Liu等［15-17］對經激光沖擊強化（laser shock processing，LSP）的鋼材料耐蝕性變化進行了研究，發現LSP可以提高材料的耐蝕性，產生晶粒細化及高強度的壓縮殘余應力并提高顯微硬度。李光雷等［18］采用分離式霍普金森壓桿（split hopkinson pressure bar，SHPB）試驗裝置對化學腐蝕后的灰巖進行了測試，研究了不同腐蝕條件下灰巖沖擊動力學性能的下降規律。Ghanadzadeh等［19］利用不同的爆炸載荷，通過測量試件的腐蝕速率，研究了沖擊載荷對低碳鋼腐蝕性能的影響，認為沖擊載荷對試件的腐蝕速率產生了影響，沖擊載荷產生的塑性變形和高密度缺陷增加了金屬試件的內能，使局部腐蝕顯著增加。

30CrMnSiNi2A高強度鋼是某型飛機受沖擊載荷結構的材料之一。本文中采用數值模擬方法建立30CrMnSiNi2A試件的SHPB試驗模型，并將材料的腐蝕等效為試件表面的腐蝕坑，對試件在沖擊載荷與腐蝕共同作用下的動力學響應進行了分析研究。

1 有限元分析方法

1.1 SHPB有限元模型

霍普金森壓桿（SHPB）是常用于測量材料在高速沖擊載荷下材料的動態力學性能的試驗裝置，主要由入射桿、透射桿、氣炮裝置、動態分析儀和數據處理系統組成，如圖1所示。本文的數值模擬計算采用ABAQUS有限元軟件進行。在ABAQUS中建立SHPB模型（見圖2），入射桿、透射桿長度為1 000 mm，子彈長度為200 mm，直徑均為14.5 mm。壓桿和子彈的彈性模量為210 GPa，密度為 7 850 kg/m3，泊松比為 0.3。為便于試件表面腐蝕坑的分布以及有限元網格的劃分，試件采用正方體的結構形式，長、寬、高均為6 mm。試件材料為30CrMnSiNi2A鋼，密度為7 720 kg/m3，彈性模量為210 GPa，泊松比0.3。試件材料塑性采用具有應變率效應的粘彈性本構Johnson-Cook模型進行描述。Johnson-Cook本構模型具有參數少、利于擬合的優點，被廣泛應用于材料的沖擊性能表征中，其模型表達式見式（1）。

式中：A為材料的初始屈服應力；B為應變硬化模量；C為應變率強化參數；n為硬化指數；m為軟化指數；Tr為參考溫度；Tm為熔化溫度。模型中所有參數可通過SHPB試驗擬合獲得。本文中30CrMnSiNi2A鋼材料試件的Johnson-Cook本構參數參考文獻［20］中的數據，忽略了溫度的影響，具體參數見表1。

表1 30CrMnSiNi2A鋼J-C本構模型參數

通過在ABAQUS有限元軟件中建立的SHPB模型，首先對無腐蝕的光滑試件進行了有限元計算，子彈入射速度設置為30 m/s，獲得了試件的應力應變曲線，此時對應的應變率為2 000 s-1。并與作為輸入參數的Johnson-Cook本構模型對比，結果如圖3所示。圖3中可見數值模擬得到的試件應力應變曲線與J-C本構模型具有較好的一致性，表明建立的SHPB模型數值計算結果可信。

1.2 腐蝕坑模型

在宏觀力學分析中，蝕坑的形狀通常被假設為是規則的，如盒形、圓柱形、圓錐形、碟形或半球形。蝕坑位置通常被假設為是均勻的分布在材料的表面，即在某一時刻，蝕坑的密度是恒定的。蝕坑大小通常由蝕坑的深度表示，可假設為服從固定的分布，如正態分布、指數分布或廣義極值分布等。Ernst等［21-22］在對腐蝕坑的生長形狀進行研究時發現在鹽溶液中，蝕坑呈半球形生長，但在后期變為半橢球形，蝕坑的深度與寬度之比與時間和溫度相關。因此，本文在數值模擬計算中將腐蝕坑等效為半球形或半橢球形。

對于有限元分析，模型的幾何形狀、接觸設置、網格類型及密度都對計算結果有著顯著的影響。在本文的分析中，忽略了SHPB試件與壓桿之間的端面摩擦，又將試件簡化為正方體，便于采用六面體網格對試件進行劃分，六面體網格的計算速度和精度都明顯高于四面體網格。因此，只對腐蝕坑附近的網格尺寸進行網格敏感度分析。

試件暫定的網格劃分如圖4（a）所示。對于腐蝕坑及其附近的區域，由于其應力分布復雜，網格密度可能對計算結果產生較大的影響。而試件其余部分應力分布相對均勻，網格密度的影響很小，為提高計算效率，網格劃分的可以稀疏一些。對側面中心點位置，直徑為0.5 mm的球形腐蝕坑采用了2種不同密度的網格，網格尺寸分別為0.04 mm和0.02 mm，應力讀取點均為積分點位置。計算得腐蝕坑最大應力值分別為2 178 MPa和2 185 MPa，基于2種網格尺寸的計算結果相差小于1%。

2 沖擊載荷對腐蝕坑應力應變分布的影響

首先對單個腐蝕坑存在時，沖擊載荷對試件應力及應變分布的影響進行了計算分析。圖5為試件側面中心點位置，直徑為0.5 mm的半球形腐蝕坑的應力和等效應變分布云圖。

腐蝕坑應力集中和應變集中發生于蝕坑底部及腐蝕坑周圍與軸向應力呈45°的方向上，應力集中最大值和最大應變位于腐蝕坑的底部。而在腐蝕坑沿沖擊載荷加載的方向上（y軸方向），應力分布則發生了分散，其應變也趨近于0。對于單個腐蝕坑存在時，沖擊載荷將會使試件在腐蝕坑底部及與沖擊載荷相交45°方向的位置成為可能的損傷源。

腐蝕坑底部中心處的應變時程曲線與無腐蝕光滑試件相同點處的曲線如圖6所示。

從子彈撞擊入射桿開始，到試件被加載完畢、試件進入卸載階段是在280μs以內完成，之后試件將不再受力，因此本文中選取280μs以內的時間段進行分析。當t=190μs時，應力波沿著入射桿傳播到達試件端面，試件開始受壓變形。應變隨時間線性增大，t=270μs時到達最大值，無腐蝕試件應變最大值為0.122 8，最大應力值為1 913 MPa；腐蝕試件最大應變值為0.300 5，最大應力值為2 178 MPa。此時，腐蝕坑導致的應力集中系數為1.139，而應變集中系數達到了2.447，應變集中系數顯著大于應力集中系數。這是因為此時的試件已經進入了塑性變形階段，相對于彈性階段，應力集中系數得到了緩和，此時的應力集中系數并不能很好地表現材料的受力危險程度。因此采用應變集中系數K來表征腐蝕坑對應力集中的影響。

式中：K為應變集中系數；εmax為腐蝕坑附近的最大應變值；εa為無腐蝕坑時該位置的平均應變。

2.1 腐蝕坑位置對試件應力集中的影響分析

為研究在沖擊作用下，腐蝕坑在試件不同位置處所受的載荷影響，分別在試件的端面和側面取編號為A～H的8個不同位置的點（圖7），并在所取點處建立直徑為0.5 mm的半球體腐蝕坑模型。每次數值計算所設置的載荷條件均相同，8個不同位置處腐蝕坑的應力云圖如圖8所示。

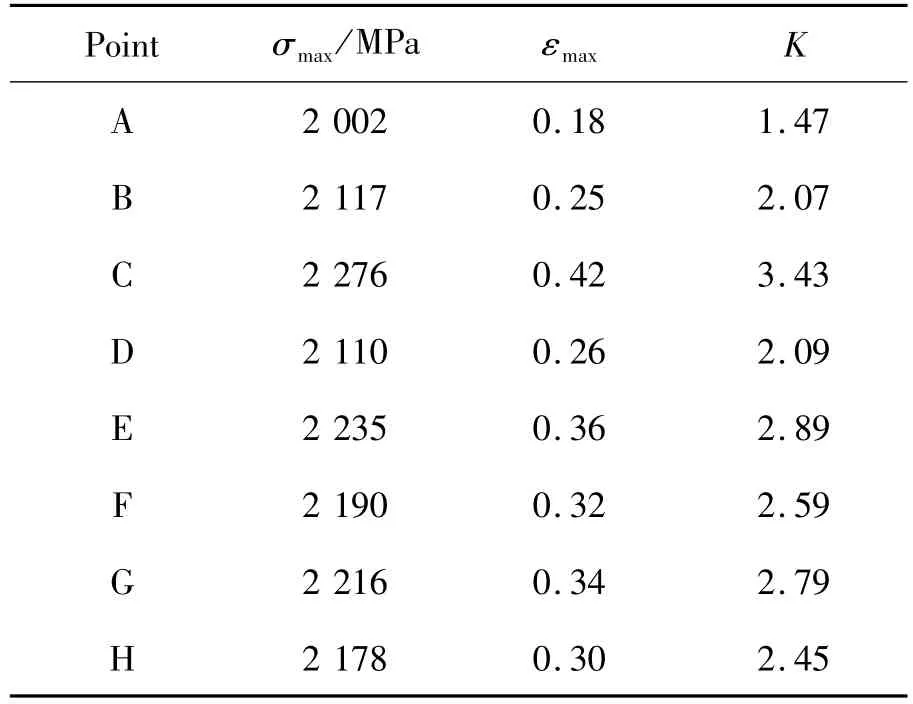
表2 不同位置腐蝕坑的最大應力和應變值

由圖8可見：腐蝕坑周圍及內部形成了明顯的應力集中，對于試件與透射桿的接觸端面，腐蝕坑最大應力集中發生于蝕坑邊緣，蝕坑底部應力分散。而試件側面的腐蝕坑應力集中發生于蝕坑底部及腐蝕坑周圍與軸向載荷呈45°的方向上，應力集中最大點位于腐蝕坑的底部，并且在腐蝕坑邊緣y軸方向上出現了應力分散。由表2可見，試件最大應變集中發生在試件頂點C處，達到了3.427，是最小處A點的2.328倍。且試件側面腐蝕坑的應力集中顯著大于端面的腐蝕坑，因此對于沖擊載荷，試件側面的腐蝕坑要比端面處的更加危險。對于試件與透射桿接觸端面，沿著端面中心點至邊緣方向的A、D、E點和A、B、C點，最大應力值均依次由小至大。腐蝕坑在端面上的應力集中呈現由中心向邊緣輻射狀的增大。對于試件側面，沿著側面中心點至邊緣方向的H、F、E點和H、G、C點，應力最大值也依次由小至大，腐蝕坑在側面的應力集中也呈現由中心向邊緣輻射狀的增大。

2.2 腐蝕坑深度對試件應力集中的影響分析

由上一節的計算可知腐蝕導致的試件側面損傷比端面損傷對材料沖擊性能影響更大。因此，為研究腐蝕坑深度對試件應力集中的影響，選取側面中心位置H點處對直徑分別為0.1、0.2、0.3、0.4、0.5 mm的半球體腐蝕坑進行了數值計算。t=270μs時刻的應變分布云圖所圖9所示。

由圖9和表3可見：對于試件側面中心點處，隨著腐蝕坑深度的增大，應變集中系數從1.930增長到2.447，應力集中影響的范圍也隨蝕坑直徑的增大而增大。試件表面腐蝕坑的直徑越大，沖擊載荷對試件的影響越大。

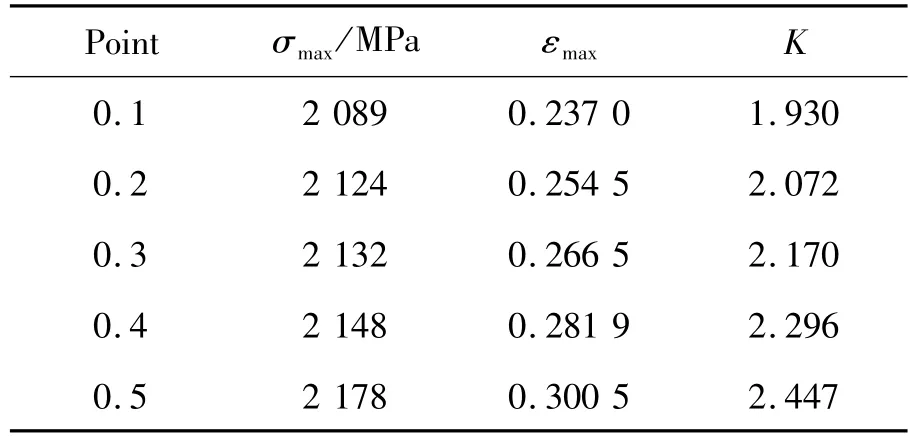
表3 不同腐蝕坑深度試件的最大應力和應變值

2.3 腐蝕坑長寬深尺寸對試件應力集中的影響

在前面的計算分析中，是將點蝕坑理想為半球形，而真實的點蝕坑有時更接近于半橢球形。因此，對半橢球形蝕坑也進行了計算，并且分析了半橢球形腐蝕坑長寬深尺寸對試件應力集中的影響。半橢球形的三維尺寸分別定義為長l、寬w、深r。長度為沿載荷加載方向（y軸方向）的腐蝕坑尺寸，寬度為垂直于載荷加載方向的尺寸。

在側面中心點H點處，每次控制長、寬、深中的其中一個參數，對3種半橢球形腐蝕坑進行了計算，蝕坑具體尺寸參數見表4。計算得應力分布云圖如圖10所示。

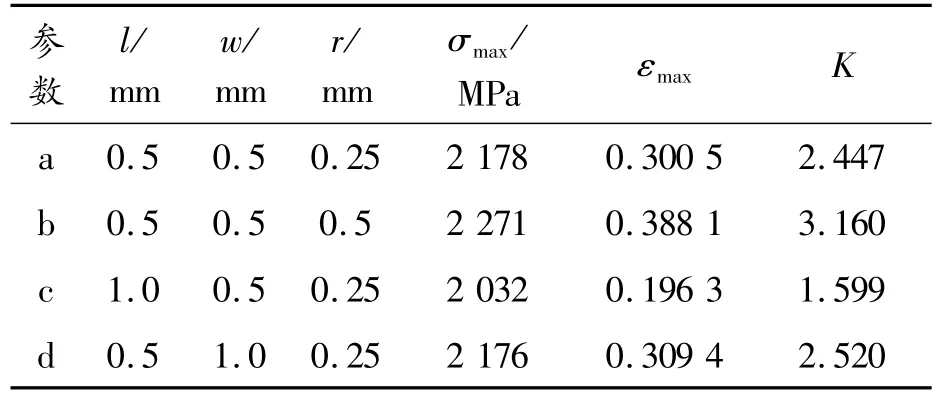
表4 不同尺寸半橢球形腐蝕坑最大應力應變值

由表4及圖10可見：蝕坑深度和長度顯著影響試件的應力集中，而蝕坑寬度的影響則很小。由圖10（a）和（b）可見：當蝕坑深度由0.25 mm增加到0.5 mm時，應變集中由2.447增加到3.160，蝕坑底部形成的應力集中隨深度增加而增加，蝕坑也越容易發展成初始裂紋。而蝕坑長度的增加卻使蝕坑的應力得到了分散，如圖10（a）、（c），長度由0.5 mm增加到1 mm，應變集中系數由2.447下降到1.599。圖10（a）、（d）可見蝕坑寬度的變化對應力和應變分布都沒有顯著影響，蝕坑寬度由0.5 mm變化到1 mm，應變集中系數由2.447變化到2.520，沒有顯著變化。這是因為寬度方向剛好與試件沖擊載荷加載方向垂直，軸向的加載對長度產生了顯著影響，而對寬度并沒有明顯影響。這也表明，對于沖擊載荷，試件軸向的結構形式對結構強度起到決定性的作用。

2.4 多腐蝕坑分布對試件應力應變分布的影響

在試件側面的縱向和橫向方向均勻分布了9個半球形腐蝕坑，腐蝕坑直徑均為0.5 mm。應變分布及各點處應變集中系數的數值計算結果如圖11所示。

由圖11可見：試件側面邊緣中心點處的應變集中系數最大，為2.548。側面應變集中呈現由中心成輻射型向四周逐漸增大，邊緣處的腐蝕坑易形成損傷源頭。從十字分布中可見軸向的腐蝕坑之間的相互影響顯著大于橫向腐蝕坑之間的影響，因此對軸向上2點蝕坑距離對應力分布的影響進行進一步分析。

2.5 相鄰腐蝕坑間距對應力應變狀態的影響

對軸向上相鄰腐蝕坑不同間距對應力分布的影響進行了計算分析。腐蝕坑沿軸向中心線對稱分布，間距分別為0.1～0.5、1 mm。由圖12、13和表5可見，應變集中最大值均在腐蝕坑底部，上、下兩腐蝕坑應變集中系數相差不大。隨著蝕坑間距的增加，兩腐蝕坑的應變集中系數隨之增大，當間距達到0.4 mm時，蝕坑應變集中達到最大值2.491。隨著間距的繼續增大，蝕坑應變集中有所回落。兩腐蝕坑同時存在時，相對于單個腐蝕坑存在的情況，應變集中被分散。

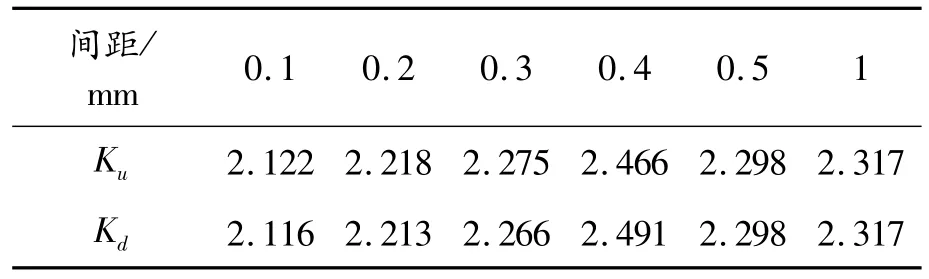
表5 不同間距相鄰腐蝕坑的應變集中系數

3 腐蝕坑對應力三軸度的影響

圖14為側面H點處不同直徑半球形蝕坑中心點O點、橫向右側和軸向頂部邊緣點R點、T點的應力三軸度曲線。對于無腐蝕試件，在試件受沖擊載荷壓縮過程中，應力三軸度始終為-1/3，表明無腐蝕的試件始終處于單軸壓縮的應力狀態下。而有腐蝕坑試件應力三軸度隨時間線性減小，試件在腐蝕坑底部處的塑性累積應變增幅變大也將使腐蝕坑處發生損傷失效的危險程度遠大于無腐蝕時的情況。蝕坑中心O點處及橫向邊緣R點的應力三軸度均趨近于-2/3位置，表明此處位置的應變類型為壓縮應變。而軸向邊緣T點的應力三軸度均趨近于0.4位置，表明此處位置的應變類型為拉伸應變。對于不同深度的球形腐蝕坑，其深度變化對蝕坑附近位置的應力狀態分布并沒有顯著的影響。

半橢球形腐蝕坑底部中心點O點、右側邊緣R點和頂部邊緣T點的應力三軸度時程曲線如圖15所示。圖中可見腐蝕坑底部O點和R點承受了壓縮應力，而T點承受拉伸應力。腐蝕坑長寬深尺寸對O點和T點的應力狀態更加敏感。腐蝕坑深度越深、軸向方向的長度越小、橫向方向的寬度越大，其底部O點處應力狀態更偏向于的壓縮應力狀態；腐蝕坑深度越深、軸向方向的長度越大、橫向方向的寬度越大，其右側邊緣R點處應力狀態更偏向于的壓縮應力狀態；腐蝕坑深度越深、軸向方向的長度越小、橫向方向的寬度越小，其右側邊緣R點處應力狀態更偏向于的拉伸應力狀態。

4 隨機點蝕損傷對應力應變狀態的影響

腐蝕坑深度取決于腐蝕速率和腐蝕時間，蔣超等［23］對高強鋼材料進行了鹽霧試驗，并對不同腐蝕時間的鋼材料點蝕坑進行了統計，擬合出了點蝕深度服從正態分布模型的分布參數。根據蔣超等［23-24］的研究，腐蝕坑深度分布服從正態分布，概率分布函數表達式為

式中：μ為平均數；δ為標準差。

隨機點蝕分布參數參考文獻［23］中的數據，取其中2組分布參數作為點蝕坑隨機分布的模型，A組：μ=83.402，δ=15.429；B組：μ=202.604，δ=38.327。點蝕概率分布如圖16所示。點蝕腐蝕坑位置分布參考文獻［24］中數據，腐蝕坑密度取1 pit/mm2。

由于材料表面蝕坑數量較多，蝕坑的深度和位置均服從概率分布，難以在ABAQUS軟件直接建立隨機分布點蝕模型。因此通過Python程序來編制蝕坑的隨機分布模型，并導入ABAQUS有限元分析軟件中。采用2組隨機分布參數分別對試件的側面和端面進行了計算，其應變分布云圖如圖17所示。

由圖17可見：2組分布下側面最大應變集中系數為4.959和3.785，端面最大應變集中系數為4.542和3.083，側面的應變集中大于端面。對于側面隨機分布的點蝕坑，點蝕坑底部及蝕坑45°方向的應力和塑性應變均顯著大于試件的平均塑性應變。點蝕的存在改變了試件表面的應力狀態，蝕坑底部容易形成損傷的初始點。在點蝕坑的軸向方向上，塑性應變趨近于0，說明點蝕坑不僅會使應力集中，也會使應力分散。在點蝕坑的45°方向上，塑性應變也大于試件的平均應變，表明在沖擊載荷作用下，蝕坑45°方向也有剪切斷裂的危險。對于端面處的隨機分布點蝕，應力集中發生與點蝕坑邊緣，對應的塑性累積應變也在此處發生累積。蝕坑底部的應力和累積應變小于試件的平均應力應變，損傷易于在端面點蝕的邊緣處發生。隨著腐蝕的加重，蝕坑深度變深，蝕坑導致的應力集中和塑性應變也逐漸增大，材料損傷的風險也將隨之增大。

5 結論

1）端面腐蝕坑最大應力集中發生于蝕坑邊緣，蝕坑底部應力分散。側面的腐蝕坑應力集中發生于蝕坑底部及腐蝕坑周圍與軸向載荷呈45°的方向上，應力集中最大點位于腐蝕坑的底部，并且在腐蝕坑邊緣y軸方向上出現了應力分散。試件最大應變集中發生在試件頂點C處，達到了3.427，是最小處A點的2.328倍。腐蝕坑在試件側面及端面上的應力集中呈現由中心向邊緣輻射狀的增大。

2）隨著腐蝕坑深度的增大，應變集中系數從1.930增長到了2.447，應力集中影響的范圍也隨蝕坑直徑的增大而增大。蝕坑深度和長度顯著影響試件的應力集中，而蝕坑寬度的影響則很小。

3）隨著蝕坑間距的增加，兩腐蝕坑的應變集中系數隨之增大，當間距達到0.4 mm時，蝕坑應變集中達到最大值2.491。隨著間距的繼續增大，蝕坑應變集中有所回落。兩腐蝕坑同時存在時，相對于單個腐蝕坑存在的情況，應變集中被分散。

4）對于隨機分布的點蝕坑，試件側面的應變集中大于端面。因此對于沖擊載荷，SHPB試件側面發生的腐蝕要比端面處的更加危險，腐蝕導致的試件側面損傷比端面損傷對材料沖擊性能的影響更大。

本文中分析了腐蝕條件下動態壓縮載荷作用下的結構響應，然而相對于壓縮載荷，腐蝕狀態下的拉伸載荷工況會更加危險，尤其是腐蝕導致的微觀缺陷會成為拉伸斷裂時的裂紋源。但是拉伸時材料的力學行為和壓縮時并不完全一致，損傷機理也不盡相同，仍需在后續的工作中深入研究。