機器人用精密減速器空載摩擦轉矩分析與測量
徐 航,何元春,吳耀庭,施 軍,謝桂平,趙新宇
(1.中原工學院 a機電學院;b計算機學院,鄭州 450007;2.寧波夏廈齒輪有限公司,浙江寧波 315202)
精密減速器具有傳動精度高、效率高、傳動比大、剛度大、體積小等優點,被廣泛應用于工業機器人等領域[1-2]。工業機器人應用減速器主要有RV減速器、諧波減速器和行星減速器。精密減速器的性能對工業機器人的性能有直接影響。工業機器人的主要技術參數包括幾何參數、運動學特性、負載特性、精度特性和重復性等。其中,幾何參數如工作空間等特征是通過機器人的關節參數來表征的;加速、位置穩定時間等運動學特性則取決于精密減速器的背隙、扭轉剛度和轉矩密度;負載特性由精密減速器的扭轉剛度、力矩負載和轉矩密度決定;精度、重復性與精密減速器的精度、可重復性直接相關[3]。
精密減速器的非線性摩擦特性是造成工業機器人遲滯特性的重要原因。國標GB/T 35089—2018將空載摩擦轉矩作為精密減速器的重要性能指標,通常需在出廠前進行測量評定,它是指在空載穩定轉速下精密減速器的摩擦轉矩[4]。目前,工業領域通常在空載狀態下從輸入端啟動精密減速器,在不同轉速下采集輸入轉矩及轉速,繪制轉矩 轉速曲線,獲得精密減速器的空載摩擦轉矩特性,見式(1)。
式中:T為空載摩擦轉矩;ω為轉速;c為常數。
部分學者從測量和控制的角度出發,研究了精密減速器的摩擦特性。呂明帥[5]分析了RV減速器的摩擦特性,建立了靜摩擦力+Coulomb+Strick+Stribeck摩擦模型;黑沫[6]分別基于 Stribeck靜態摩擦模型和LuGre動態摩擦模型,研究了諧波減速器的摩擦特性;Prasanna等[7]基于LuGre動態摩擦模型研究了諧波減速器的摩擦特性及控制策略。大量實踐表明:從低速到高速的整個過程,精密減速器的空載摩擦轉矩與轉速并不是線性關系,而是呈現出典型的Stribeck效應。因此有必要對精密減速器的空載摩擦轉矩進行深入分析和測量。
本文中對精密減速器的空載摩擦特性與模型進行分析,介紹了空載摩擦轉矩的測量原理,并進行從低速到高速的測量實驗,為精密減速器的空載摩擦轉矩性能測量與評價提供參考依據。
1 精密減速器的空載摩擦性能分析與建模
1.1 精密減速器的空載摩擦性能分析
采用油脂潤滑的精密減速器,其摩擦特性呈現出典型的Stribeck效應,即摩擦轉矩在低速階段隨轉速的增加而減小,當大于一定的轉速時,摩擦轉矩隨轉速的增加而增加[8-9],如圖 1[10]所示。
根據Stribeck摩擦理論,為了描述精密減速器在低速階段的Stribeck現象,將精密減速器的摩擦特性分為以下4個階段:
1)靜摩擦階段:在驅動力矩未達到最大靜摩擦力矩之前,精密減速器尚未轉動,摩擦轉矩主要由彈性變形所產生。
2)邊界潤滑階段:精密減速器嚙合副之間的潤滑膜尚未建立,仍為固體到固體接觸。
3)流體潤滑階段:接觸表面間形成液體薄膜,但接觸面未被潤滑劑完全分開,仍有區域為固體接觸[2,11-12]。
4)全流體潤滑階段:物體間的液體薄膜完全形成,沒有固體接觸的區域,摩擦轉矩主要取決于速度和潤滑劑的黏性系數,摩擦轉矩隨轉速的增加而增加[2,11-12]。
1.2空載摩擦轉矩 轉速曲線模型
目前,國內外的學者通常采用Tustin模型、Gaussian模型、Lorentzian模型來描述 Stribeck效應[10,13],如式(2)~(4)所示。
Tustin模型:
其中:Tf(ω)為摩擦轉矩;Tc為庫倫摩擦轉矩;Ts為靜摩擦轉矩;ωs為Stribeck轉速;B為黏滯摩擦因數;sign(ω)為符號函數。
以上3個模型均為靜摩擦模型,其中Stribeck轉速ωs可用于描述Stribeck曲線的形狀。基于空載摩擦轉矩的實際測量數據,采用合理的數據擬合方法可以獲得精密減速器精確的空載摩擦轉矩—轉速曲線。
當需要對精密減速器的摩擦特性進行精確控制時,由于 Tustin模型、Gaussian模型、Lorentzian模型均為非線性模型,存在參數識別困難等問題,因此工業領域通常基于雙直線模型進行控制,即將低速階段、高速階段的摩擦轉矩 轉速曲線分別做線性化處理,如圖2所示。其中T1、T2的表達式見式(5)。
2 測量原理
在精密減速器綜合性能測量儀上測量精密減速器的空載摩擦轉矩時,其測量原理如圖3所示。精密減速器的輸入端由伺服電機驅動,并控制其工作在速度模式下,保證測量時轉速穩定、輸出端空載。
在精密減速器運轉平穩時,其空載摩擦轉矩等價于精密減速器的輸入轉矩,如式(6)。精密減速器輸入端的轉矩通過輸入端扭轉傳感器測量獲得。
其中:Tf為精密減速器的空載摩擦轉矩;Tin為輸入端轉矩。
由于精密減速器不同嚙合位置處的受力不同,導致精密減速器不同嚙合位置的摩擦轉矩不同,在輸出端一轉范圍內,摩擦轉矩呈周期性變化。對精密減速器輸出端一轉范圍的扭矩信號進行均值濾波處理,即取扭矩的均值作為該轉速下的摩擦轉矩[14],獲得摩擦轉矩與轉速的一一對應關系,見式(7)。
3 實驗分析
基于精密減速器綜合性能測量儀(圖 4)[2,15],對某型號的RV減速器進行空載摩擦轉矩測量實驗。被測RV減速器的傳動比為121,額定扭矩為784 N·m,額定轉速為15 r/min。
3.1 空載摩擦轉矩測量
在設定工況(設定轉速、空載)下,由于不同嚙合位置處精密減速器的受力不同,導致在輸出端一轉范圍內摩擦轉矩呈周期性變化。例如在輸出端轉速為2.094 ras/s時,測得輸入端轉矩如圖5所示,表現出摩擦轉矩隨嚙合位置的變化而變化。根據式(7),由計算可得該測量轉速下的RV減速器的空載摩擦轉矩為0.208 8 N·m。
3.2空載摩擦轉矩—轉速曲線
為了準確獲得精密減速器的Stribeck摩擦效應,分別進行低速到高速的摩擦轉矩測量實驗。在低速階段,測量間隔設置較小,高速階段測量間隔可適當增大。測量獲得的RV減速器的摩擦轉矩—轉速如圖6所示。
基于Tustin模型,采用最小二乘法進行曲線擬合,獲得所測RV減速器的空載摩擦轉矩—轉速曲線如圖7所示。擬合獲得模型的各項參數如表1、2所示。
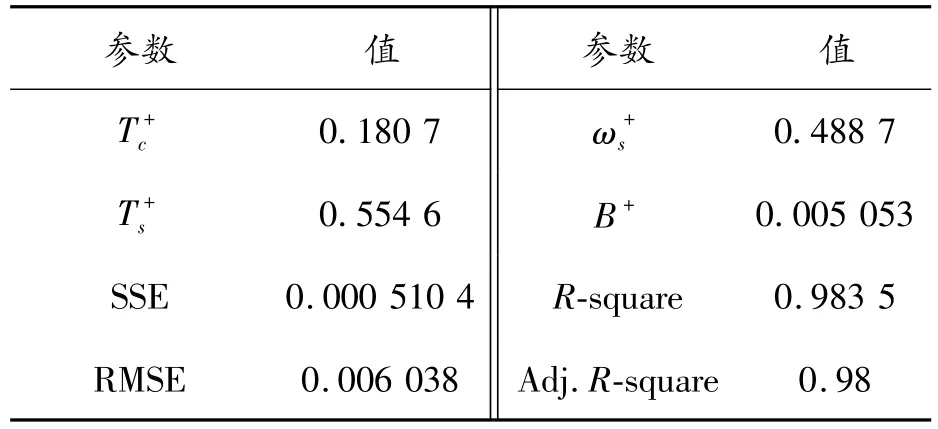
表1 RV減速器的正向擬合參數(Tustin模型)
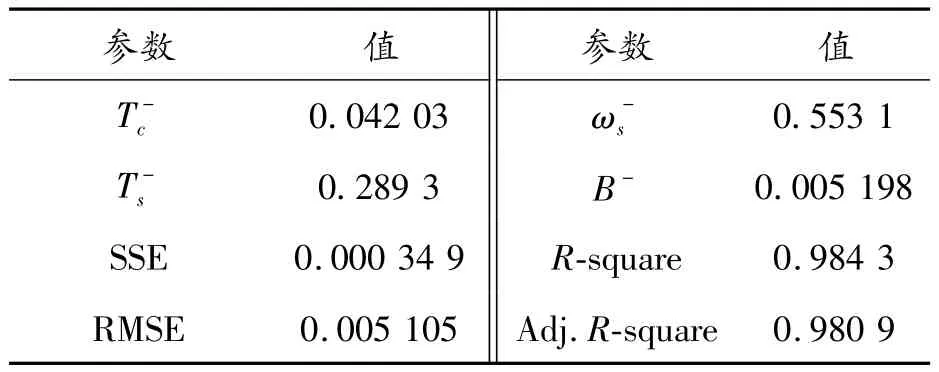
表2 RV減速器的反向擬合參數(Tustin模型)
基于Gaussian模型,采用最小二乘法進行曲線擬合,獲得所測RV 減速器的空載摩擦轉矩—轉速曲線如圖8所示,擬合獲得模型的各項參數如表3、4所示。
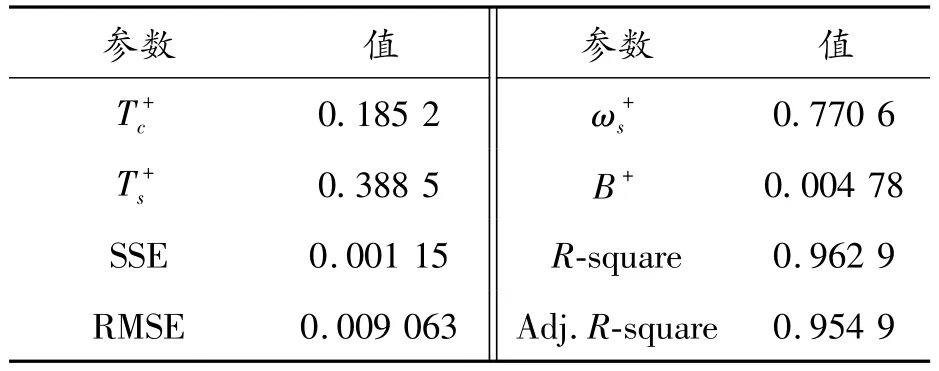
表3 RV減速器的正向擬合參數(Gaussian模型)
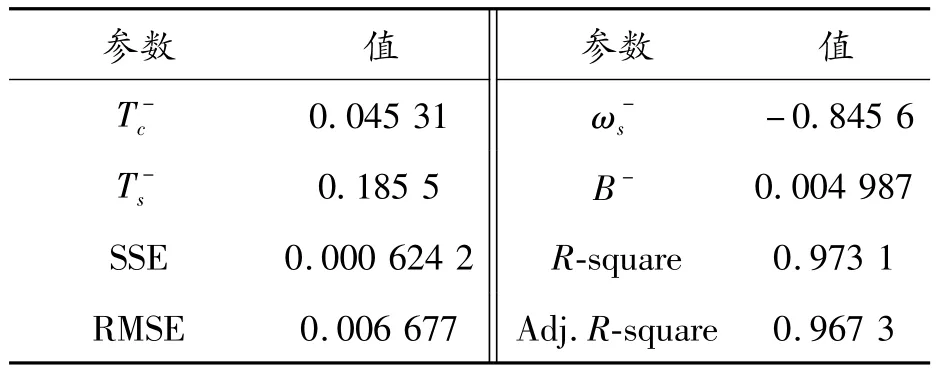
表4 RV減速器的反向擬合參數(Gaussian模型)
基于Lorentzian模型,采用最小二乘法進行曲線擬合,獲得所測RV 減速器的空載摩擦轉矩—轉速曲線如圖9所示。擬合獲得模型的各項參數如表5、6所示。
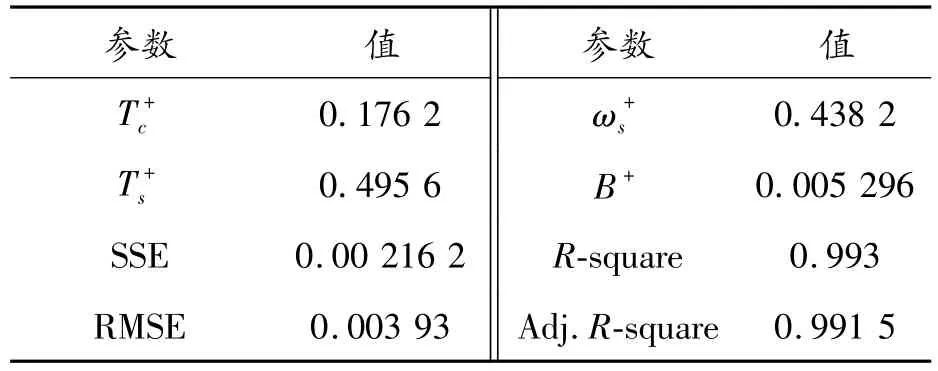
表5 RV減速器的正向擬合參數(Lorentzian模型)
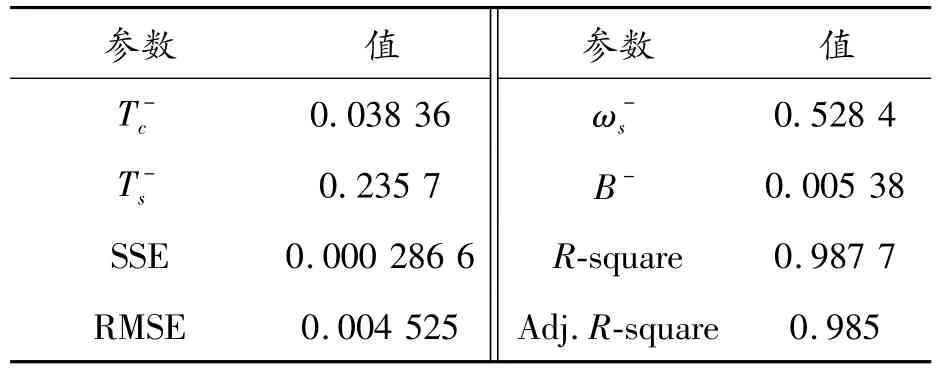
表6 RV減速器的反向擬合參數(Lorentzian模型)
3.3 擬合效果對比
對比Tustin模型、Gaussian模型和Lorentzian模型的擬合結果,可以看出3個模型的校正決定系數(Adj.R-Square)均接近1,均達到理想的擬合效果。
3個模型中,Lorentzian模型正反向的擬合參數 SSE、RMSE均最小,R-square、Adjusted R-square均最大,說明Lorentzian模型的擬合效果最佳,更適合精密減速器空載摩擦性能分析。
4 結論
1)精密減速器的空載摩擦轉矩與轉速呈現出典型的Stribeck效應,在低速階段摩擦轉矩隨轉速的增加而減小;在高速階段,摩擦轉矩隨轉速的增加而增加。
2)Lorentzian模型可以精確描述精密減速器的Stribeck效應,具有理想的擬合效果。

