基于貪婪法的配電網負荷預測設計及其案例分析

韓一鳴， 馬艷霞， 張坤， 胡志冰

(國網寧夏電力有限公司 經濟技術研究院， 寧夏 銀川 750002)

0 引言

為更好地應對當前復雜變化的經濟發展狀況，各電力企業應積極研究國家政策方向與整體電力市場環境的特點，從而對電力負荷的變化趨勢實現精確預測的過程[1-3]。目前已有多種方法可以用于負荷預測，但在使用這些預測方法的時候還有許多缺陷需要解決[4-7]。例如，選擇網格法進行負荷預測時需包含大量數據，可以利用歸一化的參數預測來獲得初始加速值，不過該方法所能達到的預測精度較低，需采取優化措施。針對以上問題，本文選擇貪婪法預測得到配電網的網格負荷加速情況，之后開發得到了經過優化的軟件，實現了預測速度的準確性的全面提升，同時也能夠彌補之前由于初加速而引起的預測誤差[8-11]。

采用貪婪算法對問題進行分析的方式是選擇現有條件下的最優決策[12]。因此，即使貪婪法并未對所有的情況都考慮在內，其目標并是追尋整體最優解[13-15]，而實際上有很多問題都可以通過貪婪法進行求解獲得整體最優解。貪婪法作為一種數據分析方法，已經被廣泛應用于分析許多實際問題。考慮到現階段國內外的經濟形勢呈現明顯的波動性，由此引起電網負荷的大幅改變，同時越來越多的分布式電源也會引起電網負荷的較大變化，對于這種情況將難以通過網格法求解得到全局最優解，同時還會占用大量時間與資源，無法達到實時預測負荷與動態調整的效果[16]。根據以上分析，本文利用貪婪法的局部最優分析方式優化了網格的負荷預測過程。

1 模型建立

1.1 流程設計

貪婪算法的一個關鍵特征是采用無后效性的選擇策略，表現為之前狀態只取決于現有狀態，而不會影響到后續過程[17-18]。因此對實際負荷進行預測的過程中，關于水平年負荷的預測先把輸入的各個數據通過最優量度標準完成排序，之后根據實際排列的順序輸入相應的參數并完成檢測過程。

貪婪算法的具體流程，如圖1所示。

圖1 貪婪算法流程

包括以下各步驟。

第一，選擇最優化貪婪度標準。

第二，驗證在上述標準下此問題可以滿足貪婪選擇性與最優子結構的條件。

第三，按照貪婪度量標準實施數據排序，確定貪婪選擇算法，求解得到可行解的子集。

第四，根據貪婪序列以及目標函數計算得到最優解。

采用貪婪算法進行計算的流程如下。

Greedy(N) /*N為候選集合*/

{

S={}; /*初始解集是空集 */

while(notsolution(S)) /*集合S不屬于問題的解*/

{

x=select(N); /*對候選集合N進行貪婪選擇*/

iffeasible(S,x) /*判斷含有x的集合S是否擁有可行解*/S=S+{x};

N=N-{x}

}

returnS;

}

1) 建立候選集合N。以該集合作為可行解，并從中選出最優解。

2) 創建解集合S。每次進行貪婪選擇后都會引起解集合S的擴展，由此獲得一個符合度量標準的完整解。

3) 建立解決函數。

4) 建立選擇函數。確定貪婪度量的評價標準，分析得到構成問題解的最佳候選對象。

5) 建立可行函數。程序包含以下運行步驟：最初解集合S保持空的狀態，根據貪婪度量標準確定選擇函數select。

1.2 負荷預測實現

貪婪算法的處理方式是先尋找各階段最優結果，通過短期處理獲得全局最優解。考慮到各階段只涉及部分信息，單獨通過計算機進行處理的貪婪算法有可能會產生最差結果。由此得到經過修改的最優解。

按照以下流程編寫貪婪選擇程序。

(1) 將原始數據P導入系統中，之后將其分配給任務表[M，N]。

(2) 根據貪婪度量標準select進行任務序列排序，并構建任務候選集合C。

(3) 確定目標函數R，對候選集合N實施貪婪選擇，其中，i=1。

(4) 從候選集N內選出具有最高優先級的任務Tk，同時移除k列，構建解集合S,j=i+1。如果j<=N,則跳轉至第4步；反之，跳轉至第5步。

(5) 當集合S不屬于問題的解時，TR=Tmax，再判斷將TR加入集合S內是否符合可行性條件。

(6) 將解集合S輸出。

2 結果分析

選擇某市3片區中的5個街區作為分析對象，先將原始數據導入系統中，再按照下述步驟進行處理。

進行貪婪選擇的具體過程，如表1所示。

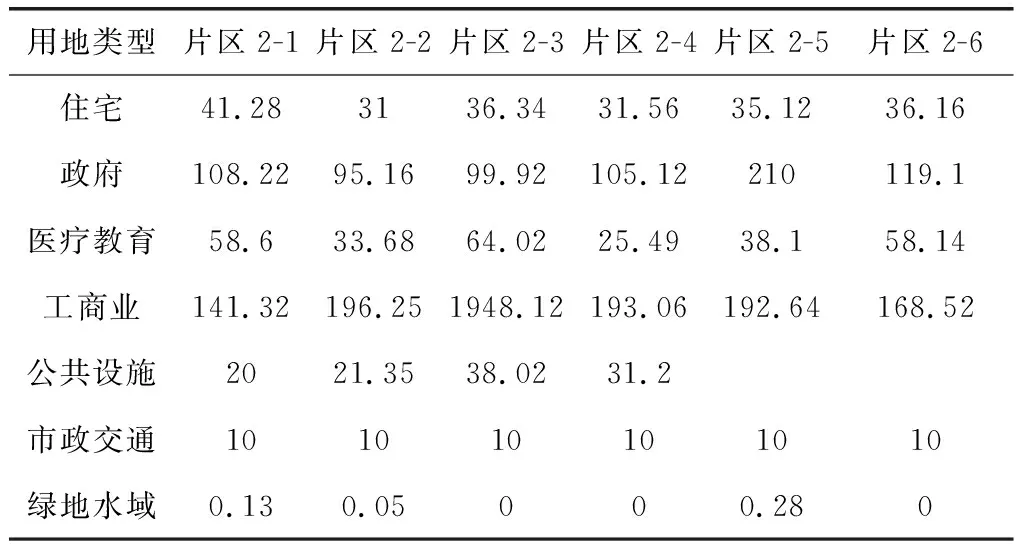
表1 貪婪選擇過程

1) 先找到具有相同數值的負荷密度數據。再將這些數據都標記成綠色，使其成為常數，確保其被排除在未來決策之外，以此作為最優負荷密度。

2) 對剩余數據按照顯著性高低順序進行排列，具有一致顯著性的數據可選擇任意方式進行排列。

3) 從隊列第一個數據開始，直至最后完成全部數值的檢查或直到最后一個無紅色標記的數值。以最后一個或多個未標記紅色的結果作為最優選擇。

本文對改進算法優越性進行了驗證，依次選擇單一網格法與利用貪婪算法進行改進后的網格法來預測各片區的負荷情況，同時計算得到二個算法的誤差比例。對1片區與2片區進行分析可以得到，如圖2所示。

其中，黑色實線是以單一網格法對負荷進行預測得到的誤差比例，藍色虛線代表通過貪婪算法改進后得到的網格法負荷預測差異性，最后將上述預測結果通過不同的圖形進行表示。

對4個片區采用兩種不同算法進行分析得到的誤差比例可以發現，對7類負荷密度利用貪婪算法改進后實現了誤差的明顯下降。誤差校正的結果顯示，住宅具備為99%，政府為34%，工商業為98%，教育醫療為78%，公共設施為100%。之后對上述各片區用地誤差實施橫向對比后發現誤差發生降低。

圖2 片區誤差比例

為更加深入采用分析貪婪算法改善網格法誤差的效果，依次從住宅、教育醫療、政府、工商業不同用地種類方面對比了各片區誤差。對典型區各類用地負荷進行預測的誤差情況，如圖3所示。

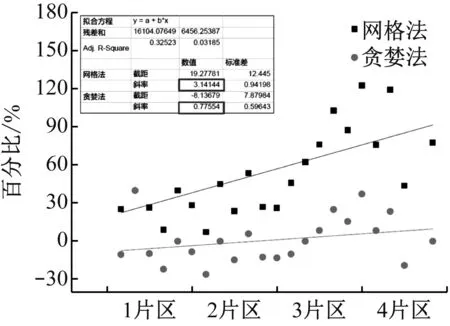
圖3 住宅負荷預測誤差結果

當擬合曲線與百分比等于0的水平線接近時，說明預測誤差很低。經測試發現采用貪婪法進行擬合可以得到更接近0的斜率。

以貪婪法改進得到的負荷預測結果除了具備更低的誤差以外，并可以有效壓縮數據的處理量。并且隨著負荷預測范圍的增大，還可以獲得更優的效果。通過綜合運用網格法與貪婪算法，可同時實現提升負荷預測速率與減少數據處理量的效果。

3 總結

對7類負荷密度利用貪婪算法改進后實現了誤差的明顯下降。誤差校正的結果顯示，住宅具備為99%，政府為34%，工商業為98%，教育醫療為78%，公共設施為100%。各片區用地誤差實施橫向對比后發現誤差發生降低。

當擬合曲線與百分比等于0的水平線接近時，說明預測誤差很低。經測試發現采用貪婪法進行擬合可以得到更接近0的斜率。并且隨著負荷預測范圍的增大，還可以獲得更優的效果。通過綜合運用網格法與貪婪算法，可同時實現提升負荷預測速率與減少數據處理量的效果。