橫風(fēng)作用下橋上車輛側(cè)傾行車安全性分析

陳 寧，李永樂，王修勇，張 淇

（1. 湖南科技大學(xué) 土木工程學(xué)院，湖南 湘潭 411201；2. 西南交通大學(xué) 橋梁工程系，四川 成都 610031）

0 引言

強風(fēng)是威脅橋上車輛行車安全性的主要因素之一，強風(fēng)不但會加劇橋梁系統(tǒng)的振動，持續(xù)不斷的振動易引起橋梁結(jié)構(gòu)疲勞和耐久性的下降，影響駕駛舒適性，而且還會進一步加劇惡化車-橋系統(tǒng)的氣動狀態(tài)，從而對通行車輛的橫向穩(wěn)定性造成嚴重影響，在風(fēng)力過大時甚至?xí)l(fā)行駛車輛發(fā)生側(cè)傾、側(cè)滑等重大交通事故，近年來，過橋車輛被大風(fēng)掀翻而引發(fā)的嚴重交通事故在國內(nèi)外的新聞報道中屢見不鮮[1-2]。

隨著“一帶一路”戰(zhàn)略的實施，交通建設(shè)向縱深推進，穿越沿海地區(qū)和艱險山區(qū)的大跨度橋梁建設(shè)得到了穩(wěn)定快速發(fā)展，這些區(qū)域風(fēng)力強勁，大風(fēng)頻率高，在如此復(fù)雜多樣的氣象環(huán)境下，存在著極大的安全隱患，對車輛的行車安全性提出了嚴峻的挑戰(zhàn)。為減少強風(fēng)環(huán)境下橋上車輛行車事故，開展大風(fēng)環(huán)境中橋上通行車輛的行車安全性評估是十分必要的，不但能有效預(yù)測事故的發(fā)生，還能為橋梁的運營和管理提供科學(xué)依據(jù)和技術(shù)支撐。

近年來，橋上車輛在側(cè)風(fēng)下的行車安全性問題日益引發(fā)國內(nèi)外學(xué)者的重視。W.H. Guo &Y.L. Xu[3]在橋面與車輪接觸點引入一個獨立的側(cè)向自由度，以便于考慮車輛相對于橋面的橫向滑移，分析了大型貨車沿大跨度斜拉橋行駛時的臨界風(fēng)速。韓萬水等[4-5]建立了考慮駕駛員行為和微觀交通流影響的風(fēng)-汽車-橋耦合振動分析模型，分析了不同類型車輛的行車安全臨界風(fēng)速限值及車-橋系統(tǒng)的動力響應(yīng)問題。李永樂等[6]針對獨塔斜拉橋，開展了廂式貨車在“干”、“濕”、“雪”、“冰”等路況條件下通過橋梁時的行車安全研究。韓艷等[7]擬合了一套考慮橋梁對車輛影響的氣動參數(shù)，并分析了這種相互影響的氣動特性對橋梁和車輛動力響應(yīng)的影響。針對車輛行駛至橋塔局部區(qū)域時，可能存在因橋面局部風(fēng)場繞流導(dǎo)致車輛氣動突變的現(xiàn)象，Rocchi 等[8]測試了大型拖掛車在通過橋塔局部區(qū)域時的平均氣動力系數(shù)，采用多體動力學(xué)模型分析了大型拖掛車的行車安全性問題。Wang 等[9]考慮橋塔局部區(qū)域?qū)囕v氣動特性的影響，分析了車輛通過橋塔時的行車安全性。Chen 等[10]采用風(fēng)洞試驗方法測試了風(fēng)屏障對車輛氣動力特性的影響，在風(fēng)-汽車-橋耦合振動的基礎(chǔ)上提出采用側(cè)傾安全因子法來評價車輛的側(cè)傾行車安全性。鑒于耦合振動的分析方法較為復(fù)雜，龐加斌等[11]通過觀察橋位風(fēng)速，采用靜力平衡的簡化方法對車輛的行車臨界風(fēng)速進行探討，Batista 等[12]針對側(cè)傾、側(cè)滑和側(cè)偏安全事故，建立了兩軸車輛靜平衡臨界風(fēng)速計算方法。熊龍[13]等采用Gumbel 極值Ⅰ型分布曲線擬合的方法確定基本風(fēng)速，并利用節(jié)段模型及全橋氣彈模型，對其顫振穩(wěn)定性進行詳細研究。許福友、周晶[14]采用風(fēng)洞試驗、數(shù)值模擬、現(xiàn)場實測3 種方法研究山區(qū)風(fēng)場特性的研究進展進行了梳理和總結(jié)，總結(jié)了山區(qū)橋址處設(shè)計風(fēng)速的幾種取值方法，為今后山區(qū)橋址抗風(fēng)設(shè)計提供參考。王玉晶等[15]采用節(jié)段風(fēng)洞模型試驗，綜合分析了不同行車工況、不同線路構(gòu)造形式及設(shè)置單、雙側(cè)風(fēng)屏障后車輛和橋梁的氣動特性。陳寧等[16]通過基于車輛氣動力和力矩等效的方法，采用等效風(fēng)速和比例系數(shù)來考慮橋面氣動繞流對車輛氣動力特性的影響。殷新鋒等[17]基于風(fēng)-車-橋耦合系統(tǒng)振動理論，分析路面等級、車速和風(fēng)速對車輛行駛安全性的影響。上述研究在車輛側(cè)傾行車安全性評估中，一方面在風(fēng)-車-橋耦合振動研究的基礎(chǔ)上，建立基于車輪接觸力的評估方法，在側(cè)傾事故分析中一般認為，車輛一側(cè)車輪脫離地面時即發(fā)生側(cè)傾事故，然而實際情況中，即使所有車輪離地車輛也不一定發(fā)生側(cè)傾事故；另一方面直接根據(jù)車輛靜力平衡條件，分析車輛的側(cè)傾事故，這種方法無法考慮車體振動對側(cè)傾行車安全性的影響。

針對上述問題，本研究中以大型集裝箱車和廂式貨車為例，推導(dǎo)了考慮鞍座約束影響的四軸拖掛車和兩軸車動力學(xué)分析模型，考慮車-橋系統(tǒng)之間相互影響的氣動力學(xué)特性，在風(fēng)-汽車-橋耦合振動研究的基礎(chǔ)上，提出在評估車輛側(cè)傾動力學(xué)穩(wěn)定平衡時應(yīng)考慮車體振動的影響，以提高車輛側(cè)傾安全性評估的準確性，分析了風(fēng)速、車速及路況條件等因素對車-橋系統(tǒng)動力響應(yīng)及車輛側(cè)傾行車臨界風(fēng)速的影響。

1 風(fēng)- 汽車- 橋系統(tǒng)分析模型

1.1 車輛動力方程

車輛動力學(xué)分析模型中，通常將具有固定幾何形狀的車體和車輪簡化為剛體，車輛懸架系統(tǒng)及車輪的剛度和阻尼簡化為彈簧和阻尼器模型。因此，車輛振動系統(tǒng)可看作由若干具有質(zhì)量的剛體，通過彈簧元件和阻尼器構(gòu)成的離散振動系統(tǒng)。車體一般考慮豎向ZV、橫向YV、側(cè)傾ΦV、橫擺φV和俯仰θV自由度，車輪僅考慮豎向ZS和橫向YS自由度。從氣動穩(wěn)定性的角度而言，空載大型集裝箱車和廂式貨車較容易受側(cè)風(fēng)的影響而發(fā)生行車安全事故。大型集裝箱車一般由牽引車和半掛車形成復(fù)雜的拖掛車列系統(tǒng)，以四軸拖掛車為例，車列由1 個牽引車體、1 個拖掛車體以及8 個車輪共10 個剛體構(gòu)成，牽引車體和拖掛車體之間通過鞍座鉸接為一個整體。四軸拖掛車輛動力學(xué)模型如圖1 所示，整車動力自由度可表示為：

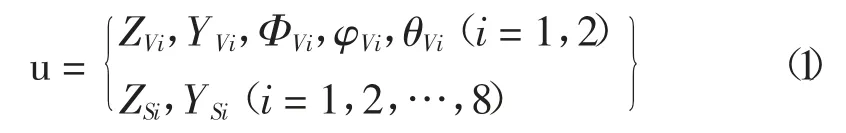
由于鞍座的約束作用，牽引車和半掛車在鞍座位置的豎向位移和橫向位移存在如下關(guān)系：

考慮自由度之間的耦合關(guān)系后，車輛共有24 個獨立的自由度，具體表示如下：

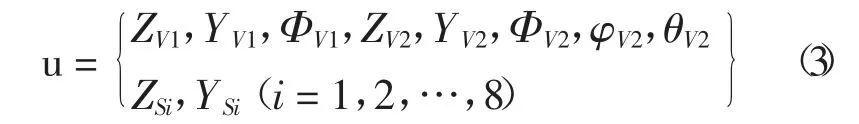
同理，兩軸廂式貨車一般由1 個車體和4個車輪共5 個剛體構(gòu)成，廂式貨車動力學(xué)模型如圖2 所示，整車模型共計13 個自由度，具體為：

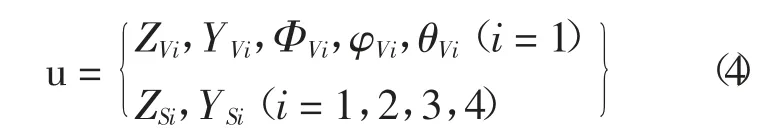
采用虛功原理建立四軸拖掛車和兩軸車動力學(xué)平衡方程，依據(jù)自由度編號順序，車輛動力學(xué)方程統(tǒng)一表達為：

式中，MV、CV、KV分別為車輛系統(tǒng)的質(zhì)量矩陣、阻尼矩陣和剛度矩陣；uV表示車輛的系統(tǒng)位移向量；f 表示作用于車輛上的荷載向量。

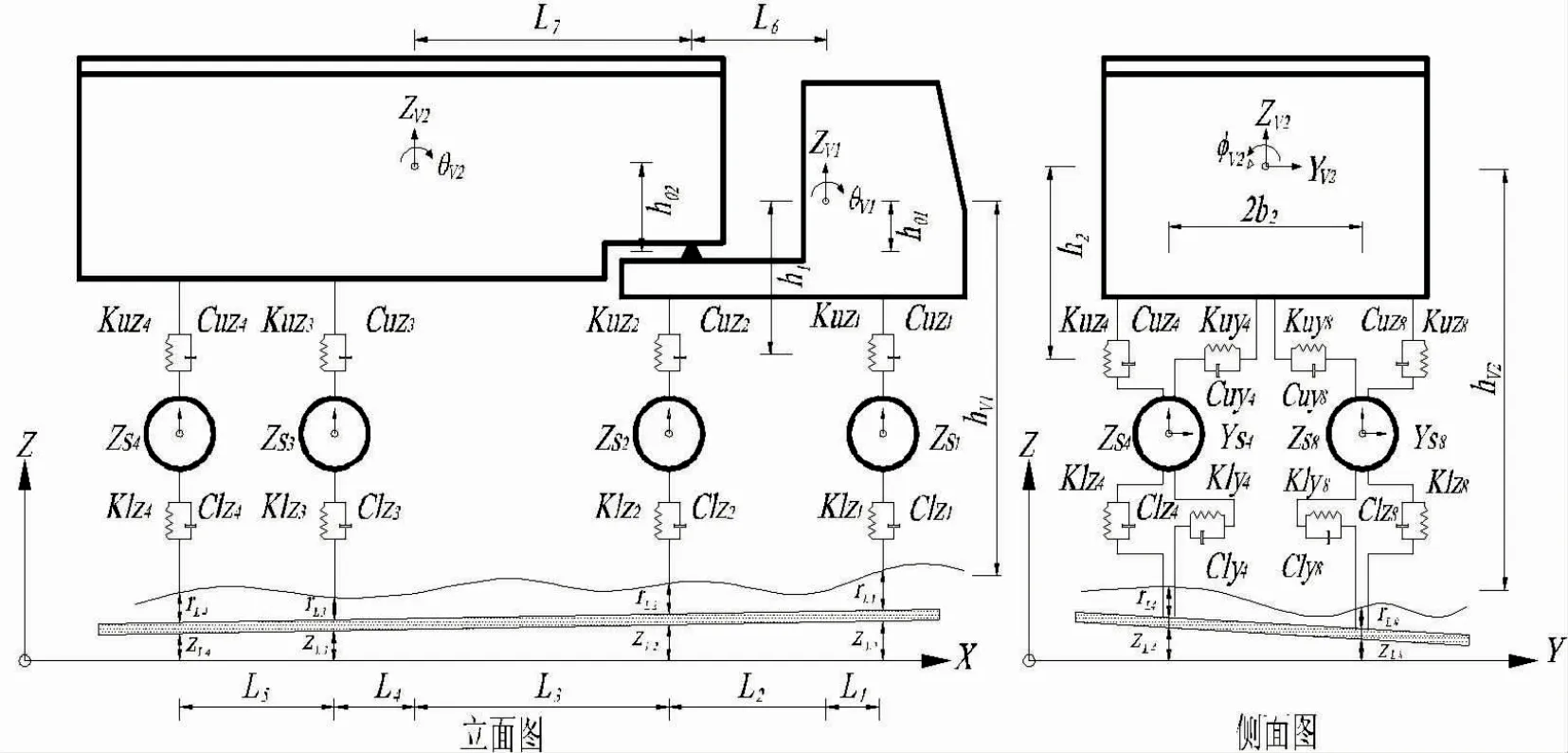
圖1 集裝箱車動力學(xué)模型Fig. 1 Dynamic model of the container truck

圖2 廂式貨車動力學(xué)模型Fig. 2 Dynamic model of the van

1.2 系統(tǒng)耦合振動方程的建立

橫向風(fēng)、汽車和橋梁三者之間的相互作用、協(xié)同工作的統(tǒng)一系統(tǒng)稱為風(fēng)-汽車-橋梁耦合振動系統(tǒng)。將橫向風(fēng)離散為空間相關(guān)的平穩(wěn)隨機過程，車輛采用質(zhì)量-彈簧-阻尼器模型，橋梁采用有限元模型模擬，風(fēng)-汽車-橋系統(tǒng)的動力學(xué)方程表示為：

式中，下標b、v 代表橋梁和車輛；fbv、fvb表示車橋系統(tǒng)間的相互作用力；fbg、fvg表示橋梁和車輛的自重；fstb、fbub表示作用于橋梁上的靜風(fēng)力和抖振力；fstv、fbuv表示作用于車輛上的靜風(fēng)力和抖振力。

路面不平度是車-橋系統(tǒng)間的重要激勵源，通常認為路面不平度是關(guān)于距離的一維平穩(wěn)隨機過程，采用功率譜密度函數(shù)描述其統(tǒng)計特性，ISO 規(guī)范[18]根據(jù)不平度系數(shù)G0表達不同等級路面之間的差異，針對“非常好”、“好”和“一般”三種等級路面，相應(yīng)不平度系數(shù)G0分別取值為 5×10-6m3、20×10-6m3和 80×10-6m3。

主梁斷面為線狀結(jié)構(gòu)，靜風(fēng)力采用定常氣動三分力表達式，抖振力采用Scanlan 建議的準定常氣動力表達式，并引入氣動導(dǎo)納函數(shù)進行修正。橋上行駛的汽車同時受到主梁繞流場和自身鈍體繞流的影響，三維氣動效應(yīng)顯著，若不計縱向氣動力的作用，作用于車輛的靜風(fēng)力采用定常氣動五分力表達式；作用于車輛的抖振力，考慮移動車輛的運動特性及水平脈動風(fēng)、豎向脈動風(fēng)對車輛抖振力表達式的影響，采用能較真實反映車輛三維氣動作用的精細化抖振力表達式[10]。由式（6a）和（6b）表達的系統(tǒng)振動方程，采用分離迭代求解具有明顯的優(yōu)勢，分離迭代法對于每一積分步，分別獨立的采用Newmark-β 數(shù)值積分法求解式（6a）和（6b），再根據(jù)兩個子系統(tǒng)間的耦合關(guān)系進行平衡迭代，在車輪和橋面接觸位置通過迭代來滿足幾何相容和力學(xué)平衡關(guān)系[19]。

根據(jù)以上理論，編制風(fēng)-汽車-橋分析系統(tǒng)（簡稱WVBANSYS V1.0，登記號2019SR0562448）程序，實現(xiàn)風(fēng)-汽車-橋系統(tǒng)的動力仿真分析。

2 風(fēng)致車輛事故評價標準

一般而言，風(fēng)致車輛事故包括駕駛失控導(dǎo)致的側(cè)偏、側(cè)滑和側(cè)向失穩(wěn)導(dǎo)致的側(cè)傾等問題[12]。側(cè)傾主要是由于車輛整體在側(cè)傾自由度上失去平衡，迎風(fēng)側(cè)車輪與地面的接觸力為零而導(dǎo)致側(cè)向傾覆。

根據(jù)平時的駕駛經(jīng)驗可知，在路況較差的道路行駛，車輛也可能在顛簸時出現(xiàn)瞬時脫離地面，豎向接觸力為零的情況，但車輛并沒有失去穩(wěn)定而發(fā)生安全事故。對于停靠在路邊的車輛而言，車輛的側(cè)傾臨界條件可以根據(jù)車輛的受力平衡條件確定。車輛側(cè)傾穩(wěn)定的條件為：

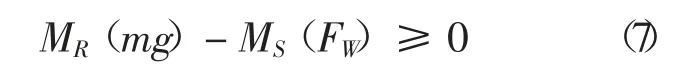
式中，MR（mg）、MS（FW）分別表示車輛自重和風(fēng)荷載對迎風(fēng)側(cè)車輪與地面接觸點的力矩。

橋上車輛在側(cè)風(fēng)環(huán)境下行駛時會同時受到側(cè)風(fēng)和橋梁振動雙重激勵的影響，車體將呈現(xiàn)出復(fù)雜的振動狀態(tài)，與靜穩(wěn)定平衡狀態(tài)相比，車輛的動力穩(wěn)定平衡方程中應(yīng)當(dāng)考慮車體瞬時慣性力的影響。車輛側(cè)傾臨界平衡受力狀態(tài)如圖3 所示，車輛側(cè)傾穩(wěn)定平衡條件為：

式中，F(xiàn)S、FL和Mx表示車輛所受的側(cè)向氣動力，氣動升力和側(cè)傾力矩；和表示t 時刻車體的豎向、橫向和側(cè)傾加速度；Mv和Ix表示車體質(zhì)量和繞側(cè)傾軸的慣性矩。上述方程可改寫為與靜力穩(wěn)定平衡時相同的表達式：

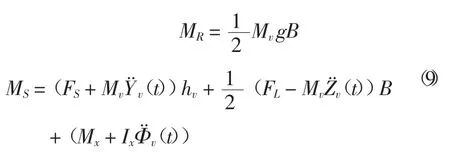
式中，MR表示表示抗傾覆力矩，MS表示傾覆力矩。通過風(fēng)-汽車-橋耦合振動分析獲得車體振動響應(yīng)時程，進而得到傾覆力矩時程曲線，當(dāng)傾覆力矩大于抗傾覆力矩時，車輛可能發(fā)生側(cè)傾安全事故。

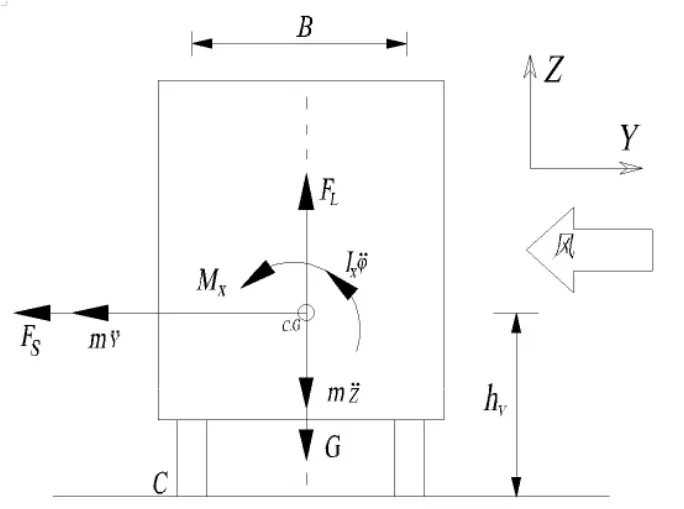
圖3 車輛動平衡極限狀態(tài)Fig.3 The dynamic equilibrium state of vehicles

3 實例分析

3.1 工程概況及分析參數(shù)

某大跨度聯(lián)跨跨海長橋全長1270 m，共由7 座連續(xù)梁橋構(gòu)成，第1、2 聯(lián)為3×45m 預(yù)應(yīng)力混凝土連續(xù)箱梁，第3-7 聯(lián)為4×50m 預(yù)應(yīng)力混凝土連續(xù)箱梁。其中，第4 座主橋的結(jié)構(gòu)形式及主梁、橋墩斷面布置如圖4 所示。橋面距海平面51.0m，A 類地表，粗糙度系數(shù)取0.12，結(jié)構(gòu)阻尼比為2.0%。

圖4 第四座橋梁總體布置圖（單位：mm）Fig. 4 The overall sketch of the firth bridge（Units: mm）

圖5 風(fēng)洞試驗中的集裝箱車和橋梁Fig. 5 The schematic of the container truck and bridge in the wind tunnel

大型集裝箱和廂式貨車側(cè)面積較大，對側(cè)風(fēng)作用較為敏感，此外空載車輛車體輕，側(cè)風(fēng)穩(wěn)定性差，更容易發(fā)生風(fēng)致行車事故。本研究主要考察空載大型集裝箱和廂式貨車的側(cè)風(fēng)行車安全性，分析車輛數(shù)目設(shè)為10 輛，車輛間距為20m，初始時刻首車位于距離橋頭50m 的路面上，路面采用ISO[18]規(guī)定“好”的道路等級。為了獲得車輛和橋梁相互影響的氣動力學(xué)特性，開展了1:20 大縮尺比節(jié)段模型風(fēng)洞試驗，試驗中來流風(fēng)速設(shè)為10m/s，風(fēng)洞中來流湍流強度≤1.5%，模型高度阻塞比為4.3%，風(fēng)洞試驗中的集裝箱車和橋梁模型如圖5 所示，試驗車輛置于第1 行車道位置，微型測力天平安裝于車廂內(nèi)車體重心位置，采樣頻率設(shè)定為142Hz，采樣時間120s，通過風(fēng)洞試驗獲得90°風(fēng)偏角時車輛的氣動力系數(shù)如表1 所示。因模型比尺較大，橋梁模型重量超過了測力天平量程，針對主梁箱型梁斷面形式，兼顧計算精度與計算效率，根據(jù)SST k-ω 湍流模型，建立二維CFD分析模型，計算得到橋梁的氣動力系數(shù)如表1所示。考慮到合成風(fēng)速的影響，橋上車輛的氣動力系數(shù)隨風(fēng)偏角變化規(guī)律可采用Baker 的統(tǒng)一氣動力表達式[10]，擬合得到的車輛五分力氣動系數(shù)如圖6 所示。

表1 車輛和橋梁的氣動力系數(shù)（攻角0°）

圖6 車輛氣動力系數(shù)Fig.6 The aerodynamic coefficients of container truck and van

3.2 橋梁和車輛的動力響應(yīng)

側(cè)風(fēng)環(huán)境下車-橋系統(tǒng)的動力響應(yīng)特性會隨著風(fēng)速、車速、路況等動力參數(shù)的變化而發(fā)生變化，本節(jié)考察不同風(fēng)速、車速對橋梁和大型集裝箱車動力響應(yīng)的影響。圖7 所示為第四座橋第二跨跨中節(jié)點的動力響應(yīng)時程，可知，風(fēng)速和車速對主梁豎向動力響應(yīng)的影響較為有限，這可能與混凝土橋梁豎向剛度較大有關(guān)。

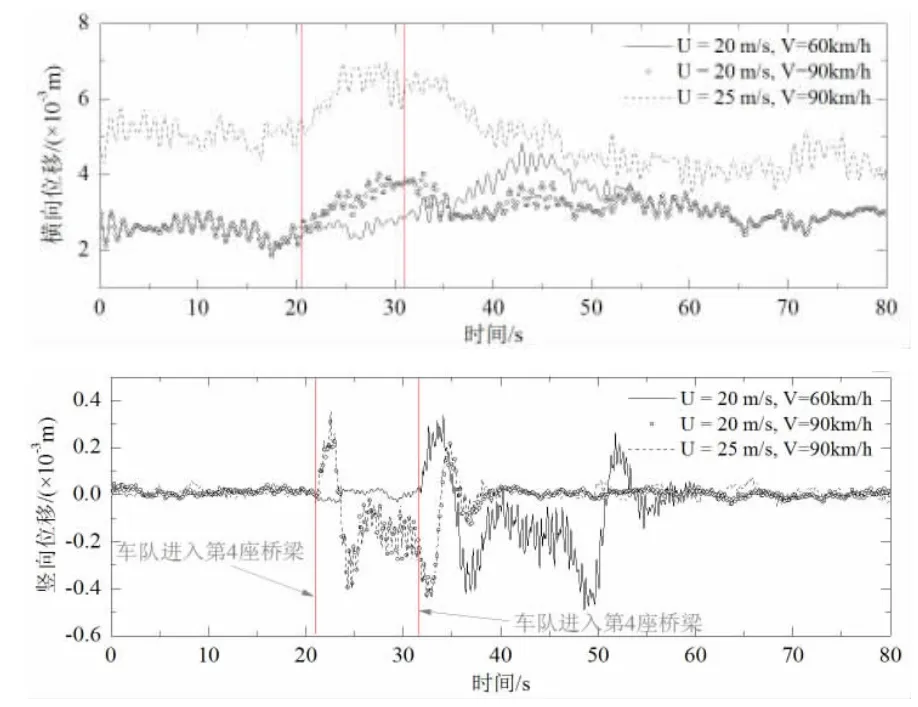
圖7 第四座第二跨跨中節(jié)點動力響應(yīng)Fig. 7 The dynamic response of the second mid-span for the forth bridge

主梁橫向動力響應(yīng)隨著風(fēng)速和車速的增加而逐漸增大，其中風(fēng)速的影響更為顯著。車隊中第五輛車（中間車） 車體振動加速度響應(yīng)如圖8 所示，車體的振動加速度響應(yīng)總體上隨風(fēng)速和車速的增大而增大，其中，車速是影響車體豎向振動響應(yīng)主要因素，而車體橫向振動響應(yīng)同時受風(fēng)速和車速的影響。車輛傾覆力矩時程曲線如圖9 所示，因受車體振動的影響，車輛傾覆力矩隨著風(fēng)速和車速的變化呈現(xiàn)出一定的隨機振動特性，風(fēng)速為25m/s 時，車輛的傾覆力矩在多個時刻超出了抗傾覆力矩值，表明車輛將發(fā)生側(cè)傾安全事故；在20m/s 風(fēng)速情況下，車輛傾覆力矩較小，不會發(fā)生側(cè)傾安全事故。

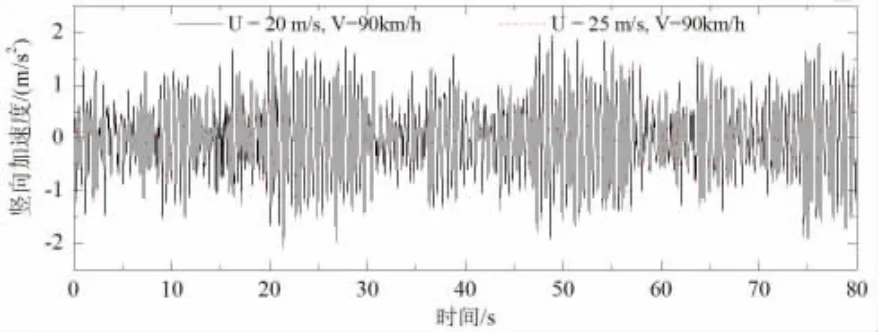
圖8 大型集裝箱車輛的加速度響應(yīng)Fig.8 The acceleration responses of the container truck

圖9 大型集裝箱車輛的傾覆力矩時程Fig.9 The overturning moment time-history of the container truck

3.3 風(fēng)速的影響

側(cè)風(fēng)是影響橋上行駛車輛行車安全性的主要因素之一。不同風(fēng)速情況下車輛以90km/h 勻速通過橋梁時，車隊中第五輛車車體振動加速度響應(yīng)如表2 所示，可知車體的橫向和側(cè)傾角加速度均隨著風(fēng)速的增大而逐漸增大，但車體的豎向加速度響應(yīng)幾乎不受風(fēng)速的影響。考慮車體振動加速度響應(yīng)對車輛側(cè)傾穩(wěn)定的影響，車輛傾覆力矩隨風(fēng)速的變化情況如圖10 所示。總體而言，傾覆力矩隨著風(fēng)速的增大而迅速增大，一方面，同一級風(fēng)速情況下傾覆力矩最大值與最小值差值區(qū)間較大，表明車輛傾覆力矩強烈的受車體隨機振動響應(yīng)的影響；另一方面，考慮車體振動時的傾覆力矩均值幾乎與不考慮車體振動時的傾覆力矩曲線重合，可知車輛的側(cè)傾行車安全性評估主要受最大傾覆力矩控制，不考慮車體振動影響可能極大的高估車輛的側(cè)傾穩(wěn)定性。對車隊中的第5 輛集裝箱車和廂式貨車而言，當(dāng)風(fēng)速分別大于25m/s 和32.5m/s時，車體傾覆力矩最大值大于抗傾覆力矩，車輛將發(fā)生側(cè)傾安全事故。

圖10 車輛傾覆力矩隨風(fēng)速變化Fig.10 Overturning moment varying with wind velocity

表2 車體振動響應(yīng)隨風(fēng)速變化

3.4 車速的影響

為進一步考察車速對橋上車輛行車安全性的影響，在20m/s 風(fēng)速情況下，車輛以不同車速勻速通過橋梁時，車體振動加速度響應(yīng)如表3 所示。由表可知，車體的豎向、橫向及側(cè)傾角加速度響應(yīng)均隨著車速的增大而逐漸增大。車輛傾覆力矩隨車速的變化情況如圖11 所示，車輛傾覆力矩均值和最大值隨著車速的增大而逐漸增大，因受最大加速度響應(yīng)的影響，側(cè)傾力矩最大值隨車速的變化較為顯著，考慮到車輛動力響應(yīng)的隨機性，大型集裝箱車側(cè)傾力矩最小值呈現(xiàn)出隨車速先增大后減小的變化趨勢。在當(dāng)前車速范圍內(nèi)，傾覆力矩最大值均小于抗傾覆力矩，表明車輛不會發(fā)生側(cè)傾安全事故。

圖11 車輛傾覆力矩隨車速變化Fig.11 Overturning moment varying with vehicle speed

3.5 路況的影響

路面不平度是車-橋系統(tǒng)的自激勵源之一，對橋上行駛車輛和橋梁的動力響應(yīng)具有重要的影響。分析了在橋面等級為“非常好”、“好”和“一般”以及路面等級為“好”四種路況條件下行駛時車輛的側(cè)傾行車安全問題。車輛以90km/h 車速在不同路況條件行駛時，最大傾覆力矩隨風(fēng)速的變化情況如圖12 所示，在同一風(fēng)速情況下，車輛的傾覆力矩基本上隨著路況的變差而逐漸增大，橋面路況的惡化會對車輛的行車安全性產(chǎn)生不利影響；同一路況情況下，地面行駛車輛的最大傾覆力矩因不受橋梁振動的影響略小于橋上行駛車輛的最大傾覆力矩。就集裝箱車而言，在路況“一般”且風(fēng)速U ＞15m/s 時，車輛將發(fā)生側(cè)傾事故，相比之下路況“非常好”時，僅當(dāng)風(fēng)速U ＞25m/s 時才可能發(fā)生側(cè)傾事故。針對廂式貨車，在路況“一般”情況下，風(fēng)速U ＞25m/s，車輛將發(fā)生側(cè)傾事故。圖13 所示為風(fēng)速20m/s 時車輛最大傾覆力矩值隨車速的變化規(guī)律。同一車速情況下路況越差，車輛的傾覆力矩越大。在路況“一般”且車速V ＞80km/h 時，集裝箱車的傾覆力矩大于抗傾覆力矩，車輛將發(fā)生側(cè)傾事故；相比而言，在當(dāng)前路況和車速范圍內(nèi)，廂式貨車不會發(fā)生側(cè)傾事故。

為了獲得不同路況情況下車輛以不同車速行駛時的側(cè)傾臨界風(fēng)速，將風(fēng)速由15m/s 至35m/s 按 2.5m/s 增量變化，車速由60km/h 至90km/h 按10km/h 增速變化，開展風(fēng)-車-橋耦合振動分析，根據(jù)最大傾覆力矩隨風(fēng)速和車速的變化情況，獲得車輛側(cè)傾臨界風(fēng)速如表4 所示。由表可知，考慮車體振動響應(yīng)影響時車輛的側(cè)傾臨界風(fēng)速隨著路況的惡化及車速的增大而逐漸降低。在車速為90km/h 且路況為“好”時，集裝箱車的側(cè)傾臨界風(fēng)速為20m/s，廂式貨車的側(cè)傾臨界風(fēng)速為27.5m/s。相比之下，采用側(cè)傾安全因子法和靜平衡估算法，集裝箱車的側(cè)傾臨界風(fēng)速分別為32.5m/s 和37m/s，廂式貨車的側(cè)傾臨界風(fēng)速分別為大于35m/s 和39.5m/s。因此，考慮車體振動影響時側(cè)傾臨界風(fēng)速遠遠低于上述兩種方法獲得的臨界風(fēng)速，表明基于輪胎接觸力的側(cè)傾安全因子法和不考慮車體振動的靜平衡估算法均會高估車輛的側(cè)傾臨界風(fēng)速，考慮車體振動影響的動力穩(wěn)定平衡方法能較為合理的評估車輛的側(cè)傾行車安全性。

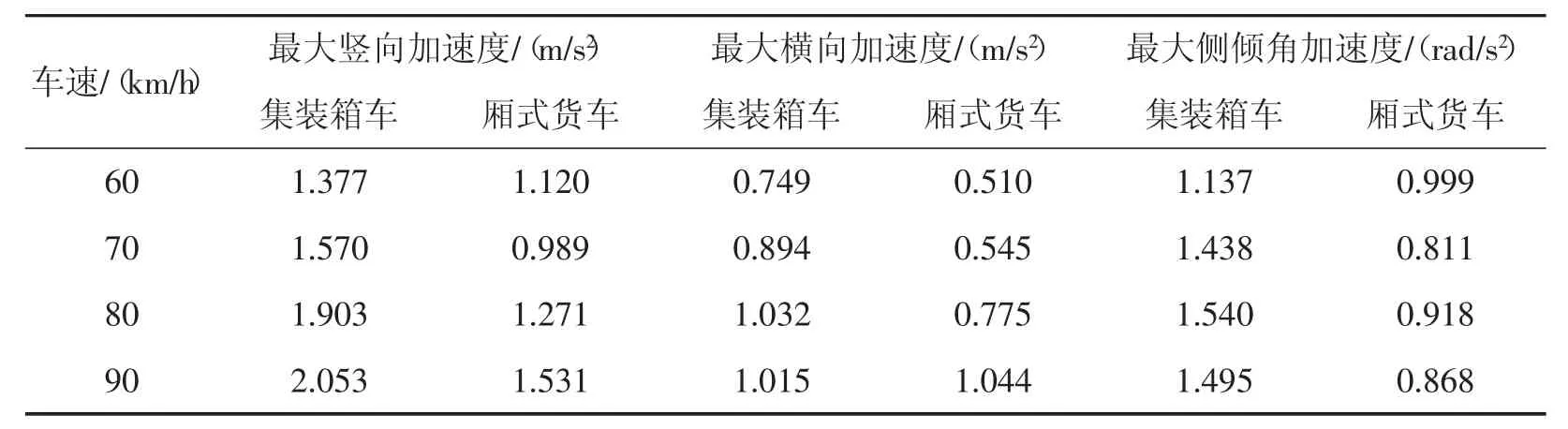
表3 車體振動響應(yīng)隨車速變化

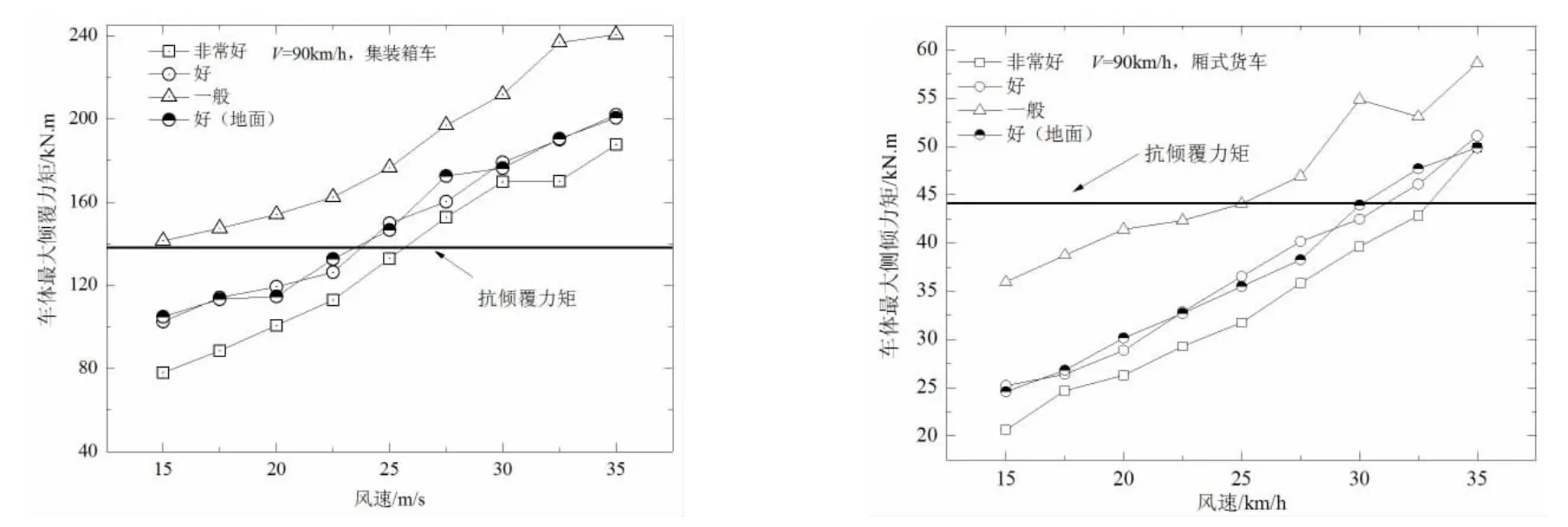
圖12 不同路況下車輛側(cè)傾力矩隨風(fēng)速變化Fig. 12 Overturning moment varying with wind velocity under different road conditions

圖13 不同路況下車輛側(cè)傾力矩隨車速變化Fig. 13 Overturning moment varying with vehicle speed under different road conditions

表4 車輛行車臨界風(fēng)速

4 結(jié)論

本文以大型集裝箱車和廂式貨車的側(cè)傾行車安全為研究對象，推導(dǎo)了相應(yīng)車輛的動力分析方程，在風(fēng)-汽車-橋耦合振動分析的基礎(chǔ)上，提出采用考慮車體瞬時慣性力影響的動力穩(wěn)定平衡方法作為車輛側(cè)傾事故的評判準則，分析了風(fēng)速、車速及路況條件對車輛動力響應(yīng)及行車安全性的影響，可得如下結(jié)論：

（1） 風(fēng)速和車速對主梁豎向動力響應(yīng)的影響較為有限，這可能與混凝土橋梁豎向剛度較大有關(guān)，隨著風(fēng)速和車速的增加，主梁橫向動力響應(yīng)呈現(xiàn)出增大的變化趨勢，其中風(fēng)速的影響更為明顯。車體的振動加速度響應(yīng)隨風(fēng)速和車速的增大而增大，因受車體振動的影響，車輛傾覆力矩隨著風(fēng)速和車速的變化呈現(xiàn)出一定的隨機振動特性，當(dāng)車輛的傾覆力矩大于抗傾覆力矩值，車輛將發(fā)生側(cè)傾安全事故。

（2） 車體的橫向和側(cè)傾角加速度響應(yīng)均隨風(fēng)速和車速的增大而逐漸增大，但車體的豎向加速度主要受車速的影響，風(fēng)速對車體的豎向加速度響應(yīng)的影響可以忽略。總體而言，車體傾覆力矩均值隨著風(fēng)速和車速的增大而逐漸增大，傾覆力矩最大值變化顯著，考慮到車輛動力響應(yīng)的隨機性，在相同風(fēng)速及車速情況下，車體傾覆力矩最大值與最小值差值區(qū)間較大，而傾覆力矩均值幾乎與不考慮車體振動時的傾覆力矩曲線重合，車輛的側(cè)傾行車安全性評估主要受最大傾覆力矩控制。

（3） 在給定風(fēng)速或車速情況下，車輛的傾覆力矩基本上隨著路況的變差而逐漸增大，表明橋面路況的惡化會對車輛的行車安全產(chǎn)生不利影響；采用動力穩(wěn)定平衡方法獲得的車輛側(cè)傾臨界風(fēng)速遠低于側(cè)傾安全因子法和靜平衡估算法獲得的側(cè)傾臨界風(fēng)速，考慮車體振動影響的動力穩(wěn)定平衡方法能較為合理的評估車輛的側(cè)傾行車安全性。在車速為90km/h 且路況為“好”時，集裝箱車的側(cè)傾臨界風(fēng)速為20m/s，廂式貨車的側(cè)傾臨界風(fēng)速為27.5m/s。