一道高考題的解法探究
例題 (2016年全國Ш卷)定義“規范01數列”{an}如下:{an}共有2m項,其中m項為0,m項為1,且對任意k≤2m,a1,a2,…,an中O的個數不少于1的個數。若m=4,則不同的“規范01數列”共有(
)。
A.18個
B.16個
C.14個
D.12個
答案:C
探究一、用分步計數原理
解:由題意,{an}中共有8項,4項為O,4項為1,且第一項為O,第八項為1,且要符合對任意k≤2m,a1,a2,…,ak中0的個數不少于1的個數。如圖l所示,此時可按項數從小到大分步作答,但關鍵是只要前面出現3個O,即結束討論,分步如下。
(1)當第二項、第三項均為O時,共C41種情況;當第三項為1,第四項為0時,共C13種情況;當第四項為1時,第五項只能為O,共C12種情況。如圖2。
(2)當第二項為1時,第三項只能為O,當第四項為O時,共C13種情況;當第四項為1時,第五項只能為0時,共q種情況。如圖3。
綜上,共有C14+C12+C12+C13+C12=14(種)。
探究二、用分類計數原理
解:由題意,{an}中共有8項,4項為0,4項為1,且第一項為O,第八項為1,且要符合對任意k≤2m,a1,a2,…,ak中O的個數不少于l的個數,分為以下幾種情況:
(1)前4項均為0,后4項均為1——共1種情況;
(2)前4項3個0,1個1,后4項1個O,3個1——共C23C13種情況;
(3)前4項2個O,2個1,后4項2個O,2個1——共2×2種情況。
所以,共有1+9+4=14(種)情況。
探究三、構造路徑問題,通過標數法解題
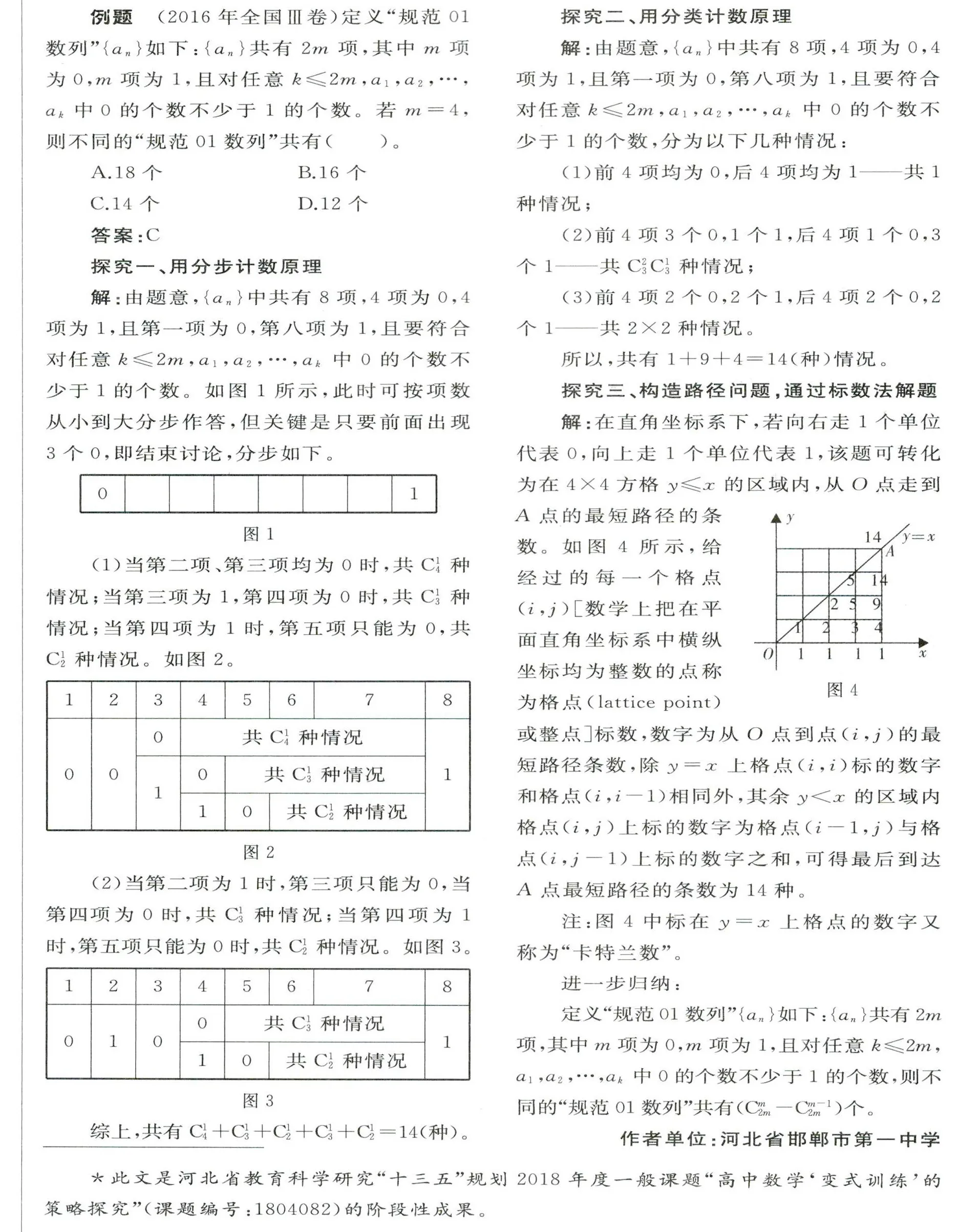
解:在直角坐標系下,若向右走1個單位代表o,向上走1個單位代表1,該題可轉化為在4×4方格y≤x的區域內,從o點走到A點的最短路徑的條數。如圖4所示,給經過的每一個格點(i,j)[數學上把在平面直角坐標系中橫縱坐標均為整數的點稱為格點(lattice point)或整點]標數,數字為從O點到點(i,j)的最短路徑條數,除y=x上格點(i,i)標的數字和格點(i,j-1)相同外,其余y
注:圖4中標在y=x上格點的數字又稱為“卡特蘭數”。
進一步歸納:
定義“規范01數列”{an}如下:{an}共有2m項,其中m項為0,m項為1,且對任意k≤2m,a1a2,…,ak中0的個數不少于1的個數,則不同的“規范Ol數列”共有個。
作者單位:河北省邯鄲市第一中學
此文是河北省教育科學研究“十三五”規劃2018年度一般課題“高中數學‘變式訓練’的策略探究”(課題編號:1804082)的階段性成果。

