房價數據的模型選擇研究
——以池州市為例

文/李濤（池州學院 大數據與人工智能學院）

住房問題一直是民生問題，合理的房產價格是經濟健康發展、人民幸福生活的一個重要指標。目前我國很多城市都出現城市房價過高、上漲過快等問題，而部分投機者也通過各種融資渠道買入房屋囤積，期望獲得高額利潤，進一步加劇了房屋價格虛高的現狀。雖然國家出臺了一系列遏制房價上漲的調控政策，但是對于具體城市而言，仍需要通過分析找出影響房價的主要原因[1-3]。本文以池州市為例，調查近些年池州房價變化情況，并根據調查的數據預測下一階段池州市房價的走勢，并結合國家和各地方政府的一系列調控房價的政策出臺時間與房價的變化情況，分析相關政策對調控房價所起的作用，對于合理判斷池州市房地產價格現狀、幫助相關部門制定調控措施、促進房地產市場健康穩健發展具有一定的現實意義。

一、商品房房價與時間的非線性模型分析

圖1 池州市商品房指數曲線圖

通過綜合國家統計局及池州市年鑒2008～2020 年的房地產相關數據，最后篩選出可能影響未來房地產價格走勢的變量，本文取定七個因素：x1：人均生產總值；x2：人均可支配收入；x3：商品零售價格指數；x4：常住人口；x5：住房竣工面積；x6：住宅投資總額；x7：居民居住消費價格指數；ym:池州市商品房房產均價[4]。R 語言程序為：X=read.csv(E:\2.csv) attach(X) plot(t,y)，初步認為ym與t 成指數關系，利用R 語言進行擬合檢驗。

對方程進行檢驗，殘差的標準差為5.122e-14，而相關系數2R1，P 值小于0.05，效果明顯，故拒絕原假設，即認為ym與t 之間存在指數關系。

對系數進行顯著性檢驗，由結果可知，a1的均方誤差為6.538e-12，b 的均方誤差為2.994e-15，而a1和b的P值均小于0.05，拒絕原假設，即認為ym與t 之間存在指數關系。

二、影響房價的多因素的多元線性回歸模型分析

建立這7 個變量關于ym的多元線性回歸模型如下所示：

式中：

β0、β1、β2、β3、β4、β5、β6、β7為未知參數，ε為隨機誤差，且認為ε服從N(0,σ2)的分布。對于式中未知參數的估計采用最小二乘法，求相關系數R2，并做顯著性檢驗，通過二者表明模型建立的是正確的[5]。為了確定商品房銷售價格與各變量之間的關系，分別作出ym與xi 的散點圖，得到散點圖如圖2 所示。

圖2 變量散點圖

利用程序cor（X）得到相關矩陣并整理得到表1：

表1 矩陣數值表

分別對ym與xi 的相關性進行檢驗，檢驗的程序為attach(X)

下列對象被屏蔽了fromX(position3):

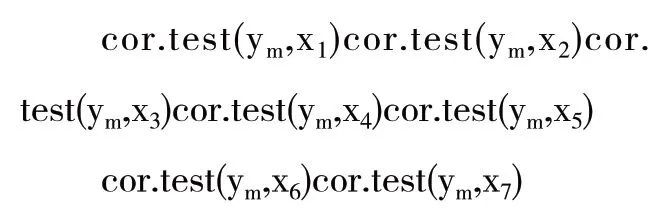
得到七個結果,綜合以上的結果可知，在0.05 的條件下，x5和x7的與ym的相關性較差，其他五個變量與ym的相關性較好，故進行多元線性回歸時，可考慮將x5和x7兩個因素排除在外。

首先對七個變量建立多元回歸方程的R 語言程序為：

得到結果如表2 所示。

表2 多元回歸方程計算結果

對方程進行檢驗，殘差的標準差為420,效果明顯，故拒絕原假設，即認為ym與各個變量之間存在線性關系。

根據P 值，選擇剔除一個變量，對回歸模型進行優化，故剔除x5，則：

Reg2=lm(ym～x1+x2+x3+x4+x5+x6+x7) summary(reg2),summary(reg2)，得到結果圖，對系數進行顯著性檢驗，由結果可知，剔除x5后，1 變的效果顯著，要保留，分析原因可能是因為x5數據偏差太大，對回歸方程造成影響偏差過大。但是變量的P值均大于0.05，故不能拒絕原假設，認為這些影響效果不明顯，可以認為這些系數為零。

對方程進行檢驗，殘差的標準差為378.7,效果明顯，且效果要好于上一次回歸的結果。故拒絕原假設，即認為ym與剔除x5后的變量之間存在線性關系。根據P 值的大小，選擇剔除變量x4，繼續對回歸模型進行優化的R 語言程序：reg3=lm(ym～x1+x2+x3+x6+x7)，summary(reg3)，得到結果圖，繼續剔除x7，Reg4=lm(ym～x1+x2+x3+x6)，summary(reg4)，對結果整理如表3所示。

表3 變量剔除多元回歸方程計算結果

對系數進行顯著性檢驗，由結果可知，β0、β1、β2、β3、β6在α=0.05條件下，均拒絕原假設，認為具有很好的效果。對方程進行檢驗，殘差的標準差為372.4，而相關系數R=0.9998，P 值小于0.05，效果明顯，故拒絕原假設，即認為ym與各個變量之間存在多元線性回歸關系。

最終分析得到回歸模型為：

三、房價預測及模型的對比評價

（一）時間指數預測模型預測房價

本文共得到兩個預測模型及其預測值，ym關于t 的指數方程：

ym=（3.220924e143）*exp(0.1681*t)，對ym進行預測的R語言程序為：

三年的預測值為：2021 年平均房價為8782.34 元；2022 年平均房價為9198.75 元；2023 年平均房價為9562.11 元。

（二）多元線性回歸預測房價

ym關于影響因素的多元線性回歸模型。在國家不出臺政策的條件下，假設7 個自變量按照符合實際的增長率增長，依次求出未來三年的各項數據，如表4 所示。

表4 池州市2021—2023年變量預測指標 單位：萬元

帶入回歸方程，則可得出多元線性方程預測的三年房價的值為：2021 年平均房價為8832.13 元；2022 年平均房價為9408.35 元；2023 年平均房價為9712.31 元。

（三）預測模型的對比評價

通過收集實際數據與兩個預測模型進行對比，可對預測的結果進行評價，得到結果如表5 所示。

表5 兩個模型預測房價與實際房價的對比 單位：元

可知，指數模型和多因素線性回歸模型均得到較好的預測值，預測偏差均非常小。根據房價時間模型，房價將隨著時間呈指數增長之勢，因此必須出臺相關政策，有效抑制房價增長。根據多元線性模型，房價與各個自變量的正負相關性就是各個變量前系數的正負。要抑制房價的上長，可以通過使系數為正的自變量增長率減少、系數為負的自變量增長率增加來達到目的。比如可以通過中央人民銀行對于貸款利率的增加，減少投資者的過度投機行為，使土地拍賣價格降低，直接降低房屋成本，同時貸款利率的增加減少了房地產商的貸款，使房地產商資金面收緊，迫使其降價賣出現有房屋，以達到回籠資金償還原來貸款的目的。