基于非線性動態逆的無人機直接升力控制

魏治強，王新華，王凱

(南京航空航天大學，江蘇 南京 211100)

0 引言

無人機直接升力控制(DLC)是通過一些操縱面直接產生升力或者側力，從而改變無人機的軌跡[1]。相比常規無人機升力必須通過機身的旋轉得到，DLC大大提高了無人機的靈活性，對于精確飛行控制以及提高機動性具有重要的意義。

針對無人機直接升力控制系統，龔華軍等[2]利用后緣襟翼偏轉所產生的直接升力抵消迎角擾動產生的氣動效果，使無人機達到中性穩定狀態，有效地加速了無人機的姿態控制。美國的MAGIC CARPET項目[3]使用直接升力控制設計了飛行軌跡角速率控制模態以及軌跡增量控制模態，提高了著艦的安全性和成功率。王亞龍等[4]針對菱形布局無人機設計了自抗擾無人機直接升力控制，解決了著陸時姿態以及軌跡控制的問題。SHAPIRO E Y Sobel[5]根據MIMO的線性小擾動無人機模型，采用特征結構配置的方法設計了直接升力以及直接側力多模態控制律。MERAT R[6]針對空客A380飛機設計了經典直接升力控制律，得出DLC能在高湍流環境下提高乘坐舒適性、提高自動著陸性能的結論。這些直接升力控制策略均采用經典的控制理論，動態解耦效果不強。

因此，本文設計了基于非線性動態逆的直接升力控制方法，在垂直機身平移模態下有效地將下沉率和俯仰角的控制動態解耦，并且擁有良好的航跡傾斜角跟蹤效果。在直接升力模態下能夠保持無人機的迎角恒定，顯著提高了航跡傾斜角控制環的帶寬。引入PID控制器和1階參考模型，魯棒性強，控制結構簡單，易于工程實現。

1 鴨式布局無人機運動模型分析

某鴨式布局無人機氣動布局如圖1所示。Og代表無人機質心位置，Oa代表無人機氣動中心，其具有水平鴨翼，雙垂尾布局。襟翼產生俯仰力矩的力臂較短，對無人機姿態的影響較小，擬用作直接升力操縱面。

該飛機對象特性的建模可以用包含12個1階非線性微分方程的方程組來描述[7]：

(1)

其中：x=[Vx,Vy,Vz,ωx,ωy,ωz,?,γ,ψ,xg,hg,zg]T，矩陣內各變量分別表示無人機三軸機體速度、三軸歐拉角速率、三軸歐拉角以及北向位置、高度和東向位置；u=[δa,δe,δT,δr,δf]T，矩陣內各變量分別表示副翼、鴨翼、油門、方向舵和襟翼出舵量；t代表時間。

采用鴨翼和襟翼用作無人機的直接升力控制面時，襟翼作為直接升力主要操縱面，鴨翼則用于平衡襟翼產生的俯仰力矩。接下來驗證該無人機使用直接升力控制方法的可行性。

(2)

在襟翼出舵角限幅為30°的情況下，此時鴨翼出舵角約為13.6°，無人機質量m=18 kg，那么直接升力控制舵面為無人機能提供最大的直接升力在±0.3 g左右，所帶來的升力控制量相當于迎角增加3.7°的升力增加量。因此襟翼和鴨翼能為無人機提供足夠的升力增量用于直接升力控制模態的設計[8]。

2 控制律設計

非線性動態逆控制系統的輸入為[9]：

(3)

2.1 航跡傾斜角動態逆控制

航跡傾斜角動態逆控制結構圖如圖2所示，其輔助輸入：

(4)

參考模型選用1階慣性系統，1/Tγ表示閉環系統期望的帶寬性能，本文設置為3 rad/s。從圖2中可以看到從參考模型1階時間導數到線性PID控制器的前饋通道，它可以消除跟蹤期望指令γc時出現的時間延遲。內環動態逆控制律由于建模誤差以及舵面操縱力矩的影響，只是近似的動態逆系統，因此線性控制器設計為PID控制器。積分環節引入對誤差的積分，消除了系統的穩態誤差。系統的輸出采用δe/δf，相比于單鴨翼輸出而言，襟翼沒有非最小相位瞬態，可以大大提升無人機的靈活性，因此提升了γ通道的帶寬。

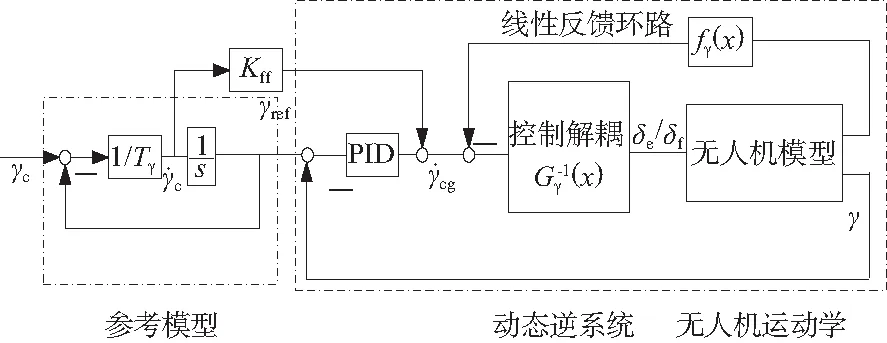
圖2 航跡傾斜角動態逆控制系統

無人機的航跡傾斜角角速率

(5)

(6)

式中：L表示升力；T表示推力；θT表示發動機的安裝角；S表示機翼有效面積。

由于直接升力控制模態和垂直平移控制模態下，鴨翼和襟翼的俯仰力矩應該相互平衡，則

(7)

聯立式(4)-式(7)可得航跡傾斜角動態逆控制律：

(8)

2.2 姿態環動態逆控制系統

根據系統的動力學方程：

(9)

式中c1、c2、…、c9可從文獻[10]中得到。

無人機的滾轉俯仰力矩方程：

(10)

聯立式(9)-式(10)可得內環動態逆控制律為：

(11)

姿態環的控制結構如圖3所示。

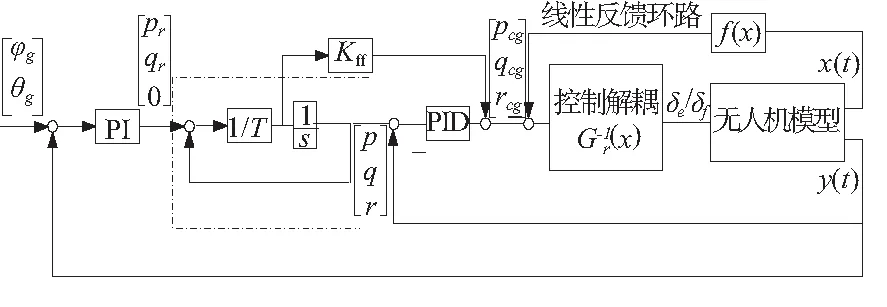
圖3 姿態環的控制結構

姿態環控制結構采用內環+外環的控制結構，內環采用航跡傾斜角動態逆相似的架構，引入前饋以及參考模型。前饋的引入提高角速率環的動態響應，而外環角度環采用經典PI控制。內回路期望航向角速率設置為0，是為了提高無人機的航向阻尼特性，改善無人機的荷蘭滾模態。

外環控制律設計為：

(12)

3 直接升力控制模態的實現

本文主要研究的是直接升力控制中的直接升力模態以及垂直機身平移模態。直接升力模態，即是在迎角保持不變(α=0)的基礎上，控制無人機的法向加速度，從而直接控制無人機的航跡傾斜角。由于Δα=0，那么在滾轉角很小的基礎上，Δθ=Δγ。垂直平移模態，即是在不改變機身俯仰角(Δθ=0)的基礎上，控制無人機在垂直方向上上下平移，Δα=-Δγ。

3.1 直接升力模態的實現

直接升力模態下控制無人機法向加速度并且保持無人機的迎角不變，航跡傾斜角動態逆控制信號到襟翼，與此同時還需要同時偏轉鴨翼，以保持俯仰力矩平衡，其示意圖如圖4所示。

圖4 直接升力模態傳動比示意圖

(13)

其中MδF和Mδe是氣動系數的導數，與無人機的(V、α)相關。為保證控制精度，僅靠開環補償是不夠的，必須加上使迎角Δα=0的閉環修正。本文選擇油門控制迎角恒定，其控制結構如圖5所示。

圖5 迎角恒定控制器

(14)

非線性動態逆直接升力模態的實現，需要斷開姿態環俯仰角的控制，使用航跡傾斜角動態逆控制系統+迎角恒定控制系統。

3.2 垂直機身平移模態的實現

垂直平移模態要求保持俯仰姿態不變的情況下，控制無人機的垂向速度。因此偏轉襟翼時，需要偏轉鴨翼以平衡俯仰力矩，其傳動比與直接升力模態相同。由于Δα=-Δγ，因此需要引入kΔα·Δα信號到襟翼輸出中，用作Δα的偏置補償，并且由于Δα改變，無人機靜穩定力矩改變，因此必須引入姿態保持系統，以平衡無人機靜穩定力矩。其傳動比結構圖如圖6所示。

圖6 垂直平移模態傳動比結構圖

由圖6可以得到：

(15)

非線性動態逆直接升力控制系統需要斷開迎角保持回路，使用航跡傾斜角動態逆控制器(加入Δα反饋偏置)+俯仰角保持系統。

4 仿真驗證

仿真分為兩部分：1)對姿態控制閉環回路進行仿真驗證，然后在保持滾轉角在配平狀態的基礎上，驗證航跡傾斜角動態逆控制器的控制性能。2)驗證本文設計的直接升力控制模態以及垂直平移模態控制器的控制性能。仿真的初始條件為H=100 m，V=30 m/s，無人機配平輸入為utrim=[0,-0.007 7,0,0,0.34,0]，配平狀態量xtrim=[29.93,0,0.628,0,0,0,0,0.021 1,0]，控制參數整定如表1所示。

表1 控制參數整定

4.1 姿態環和航跡傾斜角控制系統仿真

姿態環期望指令選取φg=θg=5°，仿真時長15 s，仿真結果如圖7所示。

圖7 姿態環動態逆控制系統響應曲線

從圖7中可以看出姿態外環的上升時間為1.8 s，調節時間為2.4 s左右，并且穩態誤差幾乎忽略不計，內環角速率誤差在2.5 s左右穩定，動態響應滿足要求。

斷開俯仰角控制器，設置期望滾轉角φg=0，期望航跡傾斜角γg=5°，航跡傾斜角動態逆控制仿真結果如圖8所示。

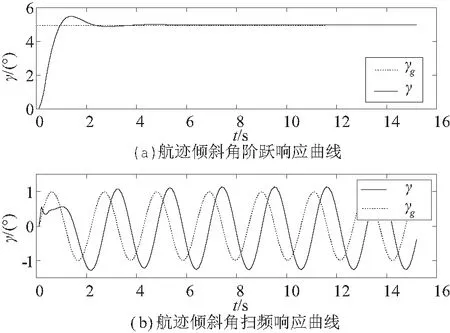
圖8 航跡傾斜角動態逆控制系統響應曲線

從圖8(a)可以看出，航跡傾斜角的上升時間為0.7 s，調節時間為1.8 s，穩態誤差為0，動態響應良好。接著用頻率3 rad/s、幅值為1的掃頻信號對閉環系統進行測試，仿真結果如圖8(b)所示。閉環響應沒有幅值衰減，但有一定的相位滯后，相位滯后約為90°，因此航跡傾斜角的帶寬約為3 rad/s，相比于常規航跡傾斜角閉環系統而言，其帶寬提高了約8倍。

4.2 直接升力和垂直機身平移模態仿真

斷開俯仰角控制器，設置期望滾轉角φg=0，期望航跡傾斜角γg=5°，加入油門迎角保持系統，測試直接升力控制模態，其仿真結果如圖9所示。

圖9 直接升力模態仿真

根據仿真結果可以看出，圖9(a)航跡傾斜角動態響應和圖8(a)基本一致，動態響應良好。圖9(b)反應了直接升力模態中θ、α、γ的變化，迎角α在2 s左右穩定在無人機的配平迎角1.2°，并且保持不變，此時Δθ=Δγ，符合直接升力模態的特征。

斷開油門迎角保持系統，設置期望滾轉角φg=0°，期望航跡傾斜角γg=2.4°，加入俯仰角控制器，設置期望俯仰角為配平俯仰角1.2°，測試垂直機身平移控制模態，其仿真結果如圖10所示。

圖10 垂直機身平移模態仿真

圖10(a)是航跡傾斜角響應曲線，垂直平移模態下，其動態響應由于迎角的減小而比直接升力模態慢，上升時間和調節時間約為4 s，沒有超調以及穩態誤差。由圖10(b)可以看出，在1.5 s以后，俯仰角進入穩態，穩定在配平俯仰角1.2°，Δα=-Δγ，在4 s以前建立法向加速度，當建立一定的迎角變化后，無人機升力減小，法向加速度趨向于0。飛機在姿態不變條件下以一定的航跡傾斜角飛行，符合機身垂直平移模態的特征。

5 結語

本文研究了一種基于非線性動態逆的直接升力控制方法，將其應用于鴨式布局無人機飛行控制系統的設計。在動態逆控制系統中加入期望指令模型，用于給出期望指令的動態過程，閉環系統的動態過程符合一般飛行品質的要求，加入參考模型到線性PID控制器的一階時間導數前饋，消除了跟蹤參考信號的時間延遲。根據姿態角和航跡傾斜角動態逆控制系統設計了直接升力模態以及垂直平移模態控制律，其動態響應良好，相比于經典連續閉環高度控制系統而言，帶寬更高，航跡跟蹤更加精確。