螺栓預緊力對振動試驗夾具動態特性的影響

王旭陽，張 磊，許紅衛，宋少偉，張允濤

(西安航天動力研究所 液體火箭發動機技術重點實驗室，陜西 西安 710100)

0 引言

振動試驗是產品性能檢驗的最常見手段，夾具作為產品與振動臺的連接件，主要用來模擬產品真實安裝環境和傳遞振動載荷，是試驗的重要組成部分[1]。夾具的模態分布情況與其傳力特性密切相關，采用數值方法開展夾具動力學分析時，螺栓連接的力學模型對其結果影響甚大。

目前最常見的處理方法是將螺栓作為剛性連接構件，在夾具底板上的螺栓孔處設置固定約束條件[2-3]，該力學模型與實際中的彈性連接方式存在較大差異，影響著夾具的傳力特性。

在螺栓結合面剛度研究方面，N L Pedersen將螺栓聯接等效成具有一定厚度的圓管，推導出結合面剛度計算公式[4]。Lehnhoff等認為螺栓結合面的壓應力呈圓錐形均勻分布，得到了同材料、同厚度連接件的剛度計算模型[5]。Wileman將有限元分析與理論計算相結合，給出了更加簡化的結合面剛度經驗公式[6]。上述文獻的推導過程中只是針對被連接件剛度進行計算，得到的結合面剛度與螺栓預緊力無關。吉村允孝法在考慮結合面特征因素的影響，推導出不同預緊力作用下，螺栓結合部剛度等效計算公式，具有廣泛的適用性[7]。

基于螺栓結合面剛度研究現狀以及振動臺結構特性，本文研究了4種不同的螺栓連接簡化模型，結合模態試驗開展對比分析，確定合適的等效動力學模型。并采用數值計算、試驗驗證與理論分析相結合的方法開展螺栓預緊力對夾具模態的影響規律分析工作，為試驗時夾具的連接螺栓扭矩確定提供參考。

1 有限元模型及模態試驗

1.1 有限元模型

夾具結構實物圖和有限元模型分別如圖1和圖2所示，試驗時，通過螺栓將夾具底面與振動臺滑臺連接。設定夾具與滑臺螺栓連接的4種簡化模型如下：

Case 1：模型中不考慮滑臺結構，在夾具底板上的螺栓孔處設定固定約束條件，為目前最常見的處理方法；

Case 2：假定滑臺為剛性結構，在螺栓預緊力作用下，夾具與滑臺的接觸面為剛性面，在數值模型中對夾具底面設置固定約束條件；

Case 3：假定滑臺為彈性結構，夾具與滑臺接觸面緊密貼合，運動具有一致性，在此采用Tie命令進行綁定，在滑臺模型上設置對應的邊界約束條件；

Case 4：將吉村允孝法運用到螺栓結合部剛度等效模型中，如圖3所示，采用一組彈簧單元來模擬螺栓連接方式，其中，一組彈簧單元包含一個法向彈簧與2個切向彈簧，彈簧兩端分別連接在夾具與滑臺螺栓孔處，并在滑臺模型上設置與Case 3工況相同的邊界約束條件。

圖1 夾具實物圖Fig.1 Fixture photo

圖2 夾具和振動臺有限元模型Fig.2 Finite element models of fixture and vibration table

圖3 彈簧單元設置示意圖Fig.3 Schematic diagram of spring units

夾具與滑臺結構材料分別為2A12和鎂鋁合金，材料性能參數如表1所示。

表1 夾具與滑臺結構材料參數Tab.1 Material parameters of fixture and vibration

1.2 螺栓結合面剛度等效模型

在研究螺栓結合部剛度問題中，國內外學者總結出了一些特定條件下結合部剛度的計算公式和經驗數據[8-10]，其中，吉村允孝研究表明，當結合面平均接觸壓力相同時，其單位面積的動態特性具有相似性[7]。可通過對結合面參數求積分獲得其等效剛度和阻尼，在此，假設作用于oxy平面的微元dxdy壓力為p，則有

(1)

式中：kz為法向剛度；kx、ky為切向剛度；k1(p)和k2(p)分別為單位面積的法向和切向剛度值。對上述公式求積分，可得任意面積的結合面剛度值

(2)

螺栓連接時，結合面接觸壓強近似呈軸對稱環形分布，上述公式等效為

(3)

如圖4所示，在螺栓預緊力作用下，結合面處的接觸壓強分布函數可用下式表述[11-12]

p(r)=aFexp(-(r-b)2/c2)

(4)

其中

F=T/kd

式中：r為接觸壓強分布半徑；T為螺栓扭矩；k為扭矩系數，通常取0.2；d為螺栓公稱直徑；a，b，c為擬合參數，與預緊力F數值無關[13]。

研究表明[14]，如圖4所示結合部剛度與接觸壓強密切相關，存在以下關系

k1(p)=αpβ(r)

(5)

式中α和β為與結合面特性相關的常數。

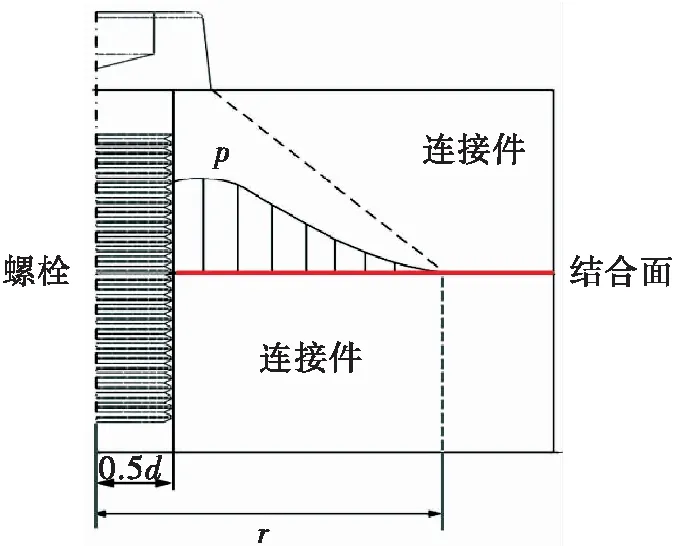
圖4 結合面接觸壓強分布情況Fig.4 Distribution of contact pressure on the bolted joint interface

結合式(3)～式(5)，可得結合面法向剛度

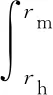
(6)

式中：rh、rm分別為結合面接觸壓強最小、最大半徑；α1和β1為與結合面法向特性相關的常數。

同理，根據吉村允孝法，結合面切向剛度

(7)

1.3 夾具模態試驗

為檢驗4種不同螺栓連接簡化模型的有效性，開展對應的夾具模態試驗。夾具通過M12螺栓與滑臺連接，螺栓擰緊力矩均為72 N·m。其中，試驗模型由27個點組成，每個點均采用三向傳感器測試。為保證試驗結果的完整性，根據結構特點，激勵點取11號、17號及19號點，激勵方向包括水平和垂直方向，脈沖激勵由試驗力錘敲擊產生，分析范圍為：0～2 048 Hz，頻率分辨率為1 Hz，通過對試驗數據處理分析，得到夾具的各階模態頻率如表2所示，振型如圖5所示。

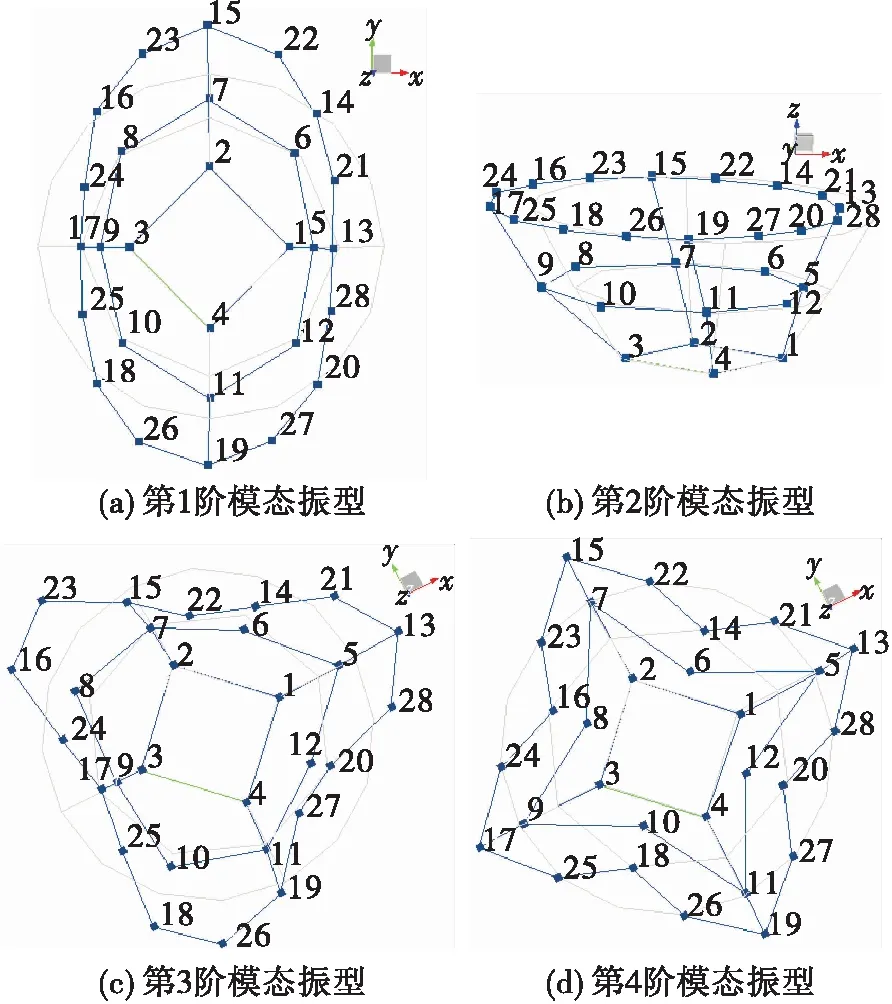
圖5 夾具前4階模態振型Fig.5 The first four modal shapes of fixture

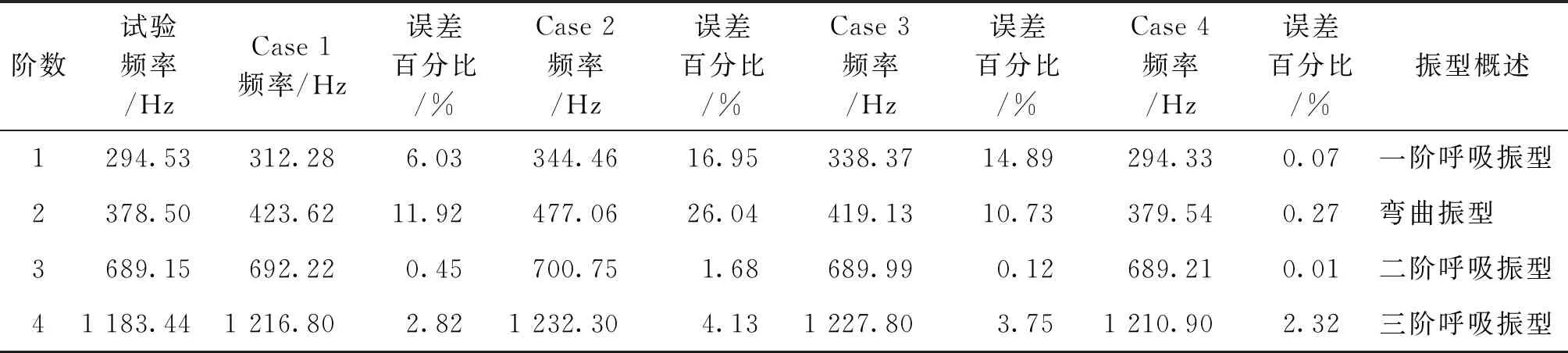
表2 數值計算模態與試驗模態結果對比Tab.2 Comparison of modal calculation and modal test results

1.4 對比分析

基于1.2節的螺栓結合面剛度等效模型，結合試驗時M12螺栓的結構特性，參考王磊等[13]給出的擬合參數取值范圍，取a=1.26、b=9.6、c=13.2、rh=6.4 mm、rm=40 mm。螺栓扭矩T=72 N·m，參考張學良等[15]給出的接觸結合面特征系數，取α1=20 644、β1=1.7、α2=561 280、β2=0.31。將上述參數代入式(6)～式(7)中可得螺栓結合面法向和切向剛度分別為Kz=1.011 2×1010N/m，Kx=Ky=4.7827×109N/m。從數值計算結果可知，4種螺栓連接簡化模型的前4階模態振型具有一致性，圖6顯示了Case 4模型中夾具前4階模態振型圖，各階模態振型均與試驗結果吻合較好。

表2總結了4種簡化模型與試驗模型的前4階固有頻率數值，其中Case 2和Case 3模型中前2階固有頻率數值誤差均大于10%，在Case 2模型中第2階固有頻率處達到峰值26.04%。與前兩者模型相比，Case1模型中第1階、第2階固有頻率數值誤差有所降低，分別為6.03%、11.92%。在Case 4模型中，各階固有頻率數值誤差均大幅度降低，前3階固有頻率數值誤差均小于1%，第4階處誤差僅為2.32%。上述結果說明，將螺栓連接方式轉化為彈簧單元的方法具有較高的動力學特征等效精度，因此在后續的數值計算中均采用該種邊界等效方法。

圖6 Case 4模型中夾具前4階模態振型圖Fig.6 The first four modal shapes of fixture in the Case 4 model

2 不同螺栓預緊力作用下夾具模態分析

2.1 數值計算結果

針對Case 4模型，采用數值計算與試驗驗證相結合的方法開展不同螺栓預緊力狀態下的夾具模態分析工作，其預緊力設置為10、15、20、25、30、35、40、45 kN共8種工況。不同預緊力下螺栓結合面的法向、切向剛度分別按照式(6)～式(7)計算。如圖7所示，當預緊力小于20 kN時，結合面切向剛度大于法向剛度。隨著預緊力的增大，法向剛度值遞增速率顯著增大，與切向剛度的差值呈快速遞增現象[16-17]。

從試驗情況和數值計算結果可知，不同螺栓預緊力作用下，夾具的前4階模態振型均與1.4節中Case 4模型振型相同。圖8展示了2種研究方法中不同預緊力作用下夾具的模態頻率變化情況，從圖8中可知，數值計算結果與試驗結果吻合度較高，近一步驗證了上述螺栓結合面等效模型的有效性。

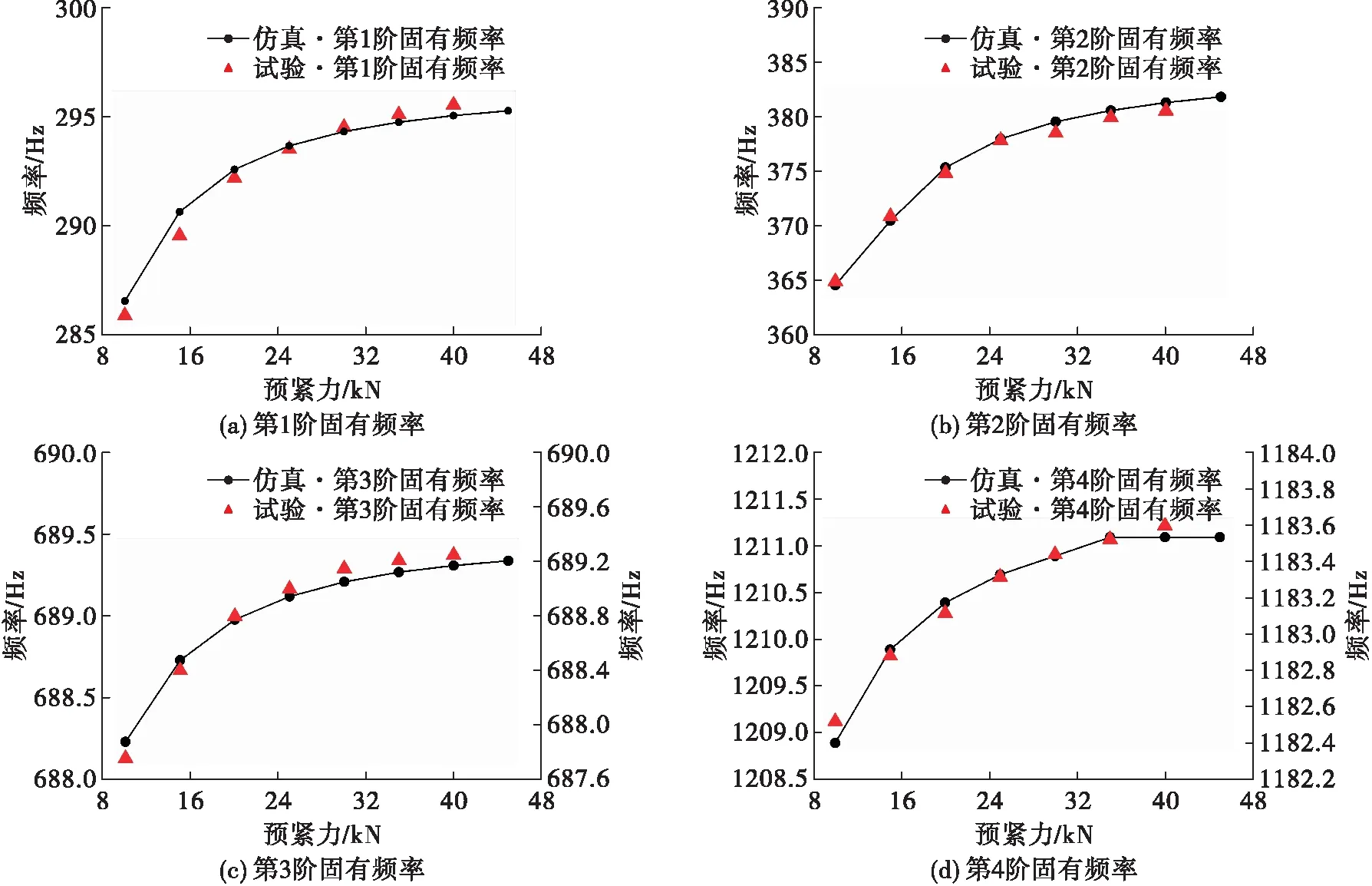
圖8 不同預緊力作用下夾具前4階固有頻率Fig.8 The first four modal frequencies of fixture under different bolt pre-tightening forces

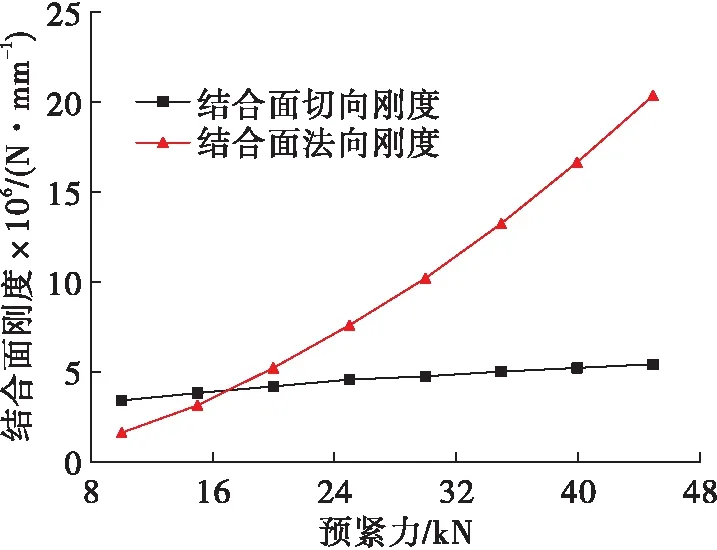
圖7 不同預緊力作用下結合面剛度Fig.7 Stiffness of bolted joint interface under different bolt pre-tightening forces

當螺栓預緊力呈線性增加時，夾具前4階固有頻率數值均呈對數函數趨勢增長，當預緊力大于30 kN時，其遞增趨勢逐漸趨于平緩。螺栓預緊力從10 kN增大至45 kN時，夾具前4階固有頻率數值增幅分別為8.74、17.22、1.11、2.2 Hz，說明預緊力對夾具前2階固有頻率數值有顯著影響。當螺栓預緊力大于35 kN時，夾具第4階固有頻率數值趨于定值1 211.1 Hz，可以預判隨著螺栓預緊力的再增大，夾具各階固有頻率數值均逐漸趨于定值，此時所對應的螺栓預緊力即為飽和預緊力，當螺栓預緊力大于此值時，其模態振型和固有頻率不發生改變，但可能會由于過大的扭矩造成螺栓鎖死，亦對滑臺鋼絲螺套造成損傷。因此，試驗時螺栓的最大預緊力值推薦取飽和預緊力值。

2.2 振動力學模型

試驗過程中，振動能量從振動滑臺傳遞到夾具上，簡化的振動試驗系統力學模型如圖9所示[18-20]，將螺栓連接方式等效為一組三向彈簧單元。

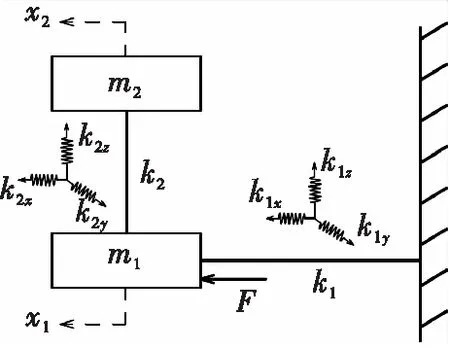
圖9 振動試驗力學模型Fig.9 Mechanical model of vibration test

在振動試驗時，滑臺受到水平(x)向推力F作用，不考慮結構在切向(y)和垂向(z)的運動，根據牛頓第二定律建立振動試驗系統水平(x)向數學模型[21]

(8)

式中：m1為滑臺質量；m2為夾具質量；k1x為滑臺與端部牛頭的連接螺栓水平向剛度；k2x為夾具與滑臺的連接螺栓水平向剛度。

設上式齊次方程(自由振動方程)有如下形式的簡諧解

(9)

式中w為圓頻率。

將式(9)代入公式(8)中的齊次方程中，可得力學模型存在意義的解為

(10)

求解可得

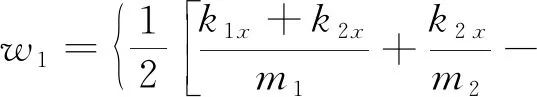
(11)

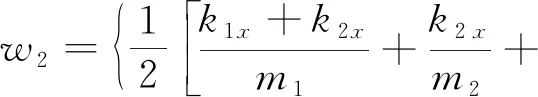
(12)

式中w1和w2分別為力學模型的1階、2階圓頻率，其與外載荷F無關，僅取決于模型體系的質量分布和剛度分布，是體系固有性質。可根據f=w/2π求得模型體系的1階、2階固有頻率。

根據滑臺和夾具結構特性可知，m1=153 kg，m2=46 kg，當螺栓預緊力在10～45 kN之間變化時，可根據式(7)計算得到單個螺栓結合面切向剛度值Kx，夾具底面17個固定螺栓存在并聯關系，則k2x=17Kx。由滑臺結構特征級正弦掃描試驗可知其第1階固有頻率為850 Hz，則k1x=m1(2πf1)2。將相關參數代入上述公式中，所得模型體系第1階固有頻率隨預緊力變化情況如圖10所示。不同預緊力作用下，力學模型體系的固有頻率變化趨勢與2.1節數值計算結果相似，從理論方面驗證了本文數值計算結果的可靠性。

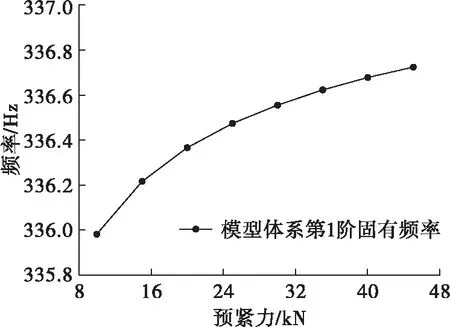
圖10 力學模型體系第1階固有頻率Fig.10 The first modal frequency of mechanical model system

3 結論

本文首先設置了4種不同的螺栓連接方式數值計算模型，結合模態試驗，確定出合適的等效動力學簡化模型，并采用數值計算、試驗驗證與理論分析相結合的方法開展螺栓預緊力對夾具模態的影響分析，所得結論如下：

1)4種簡化模型的各階模態振型均與試驗結果保持一致，其中，彈簧單元簡化模型的前3階頻率誤差均小于1%。

2)螺栓預緊力在10～45 kN遞增時，夾具各階模態振型不發生改變，固有頻率數值呈對數函數趨勢增長，存在飽和預緊力現象。

3)簡化振動試驗系統力學模型中第1階整體模態頻率隨著預緊力的變化趨勢與數值計算結果具有一致性。