向量在二面角等相關問題中的應用

潘朝毅，馬玉雯

（成都師范學院 數學學院，成都 611130）

同濟版高等數學教材[1]將兩平面的夾角θ 定義為兩平面的法線向量n1與n2所夾的銳角（或直角），. 但在立體幾何中的二面角φ 要么與θ 相等，要么為θ 的補角，因此需要先行觀察去判斷該二面角是鈍角還是銳角，才能在前面求出θ 的基礎上確定φ 值. 在很多二面角相關問題中，僅靠觀察是無法確定到底是鈍角還是銳角，這種觀察的方法嚴格講也是不嚴謹的. 而要不加入人工觀察，則需進一步限定所討論的二面角內的兩個平面法向量n1與n2的方向為“一進一出”，這時就唯一確定了

利用確定向量積方向的右手法則，選取兩個平面法向量n1與n2的方向為“一進一出”很容易. 本文將利用空間向量的線性運算及混合積、向量積的運算規律及性質，給出其在二面角相關問題的若干應用.

1 已知兩平面π1 與π2 所構成的二面角內有點M0，求該二面角的角度φ

設平面πi方程為Aix + Biy + Ciz + Di= 0，則法向量ni={ Ai,Bi,Ci}，同時記Mi( xi,yi,zi)為平面πi中的任一點，i = 1,2. 將M0( x0,y0,z0)坐標代入πi方程左端得

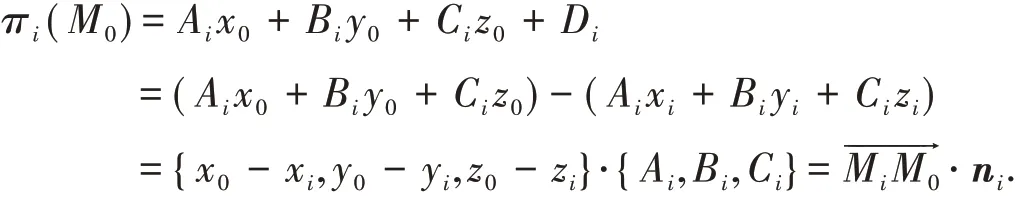
由于M0( x0,y0,z0) 是二面角內的點，故πi( M0) ≠0，而平面πi的法向量ni方向對此二面角當πi( M0) ＞0 時為“進入”，當πi( M0) ＜0 時為“出離”. 故此得到結論：

將M0( x0,y0,z0) 坐標分別代入兩平面方程左端計算，若兩值異號，則二面角的角度

解析幾何教材[2]中規定平面π 的法式方程為xcosα + ycosβ + zcosγ - p = 0 時，特別要求p 非負，本質上就是確保n0={ cosα,cosβ,cosγ } 為從原點指向平面π 的單位法向量，此即通過πi( M0) ＜0 來保證ni={ Ai,Bi,Ci}是從點M0( x0,y0,z0)指向平面πi的法向量的特例.

2 用向量工具證明三面角余弦定理

三面角余弦定理在求解某些二面角問題時有獨特優勢[3]. 利用向量的混合積運算性質和雙重向量積公式，可以很簡潔地證明該定理.

引理1a ?( b × c )= ( a × b )?c

引理2( a × b )× c = ( a ?c ) b - ( b ?c ) a

定理1（三面角余弦定理）四面體（三棱錐）O - ABC 中，記∠AOC = α,∠BOC = β,∠AOB = γ,二面角A - OC - B = φ，則

證明：記的單位向量為a,b,c，則∠( a,c )= α，∠( b,c )= β，∠( a,b )= γ. 注意到若取平面AOC 的法向量為a × c，平面BOC 的法向量為b × c，這兩個方向對于二面角A - OC - B 一定為“一進一出”，由于

故cosγ = cosαcosβ + sinαsinβcosφ.

3 空間已知兩點M1 與M2 所在平面發生折疊后，求兩點的距離

設空間某平面π 上兩點M1( x1,y1,z1) 與M2( x2,y2,z2) 在π 上一條直線L 的兩側，沿直線，這里( x0,y0,z0) 是直線L 上一點M0的坐標，{ cosα,cosβ,cosγ )是直線L 的單位方向向量v0的坐標，為點M1,M2折疊后的新位置. 下面我們利用向量工具推導出計算折疊后兩點間距離d()的公式.

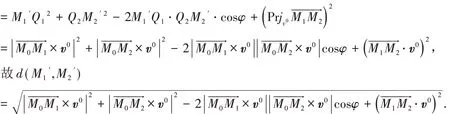
如果考慮點M1與M2及直線L 在平面直角坐標系xoy 的特殊情形，即已知坐標M1( x1,y1)與M2( x2,y2)及直線方程Ax + By + C = 0，那么直線的單位方向向量，若記f ( Mi)= Axi+ Byi+ C，i = 1,2. 注意到M1與M2在直線L 兩側，所以f ( M1) f ( M2) ＜0，因此

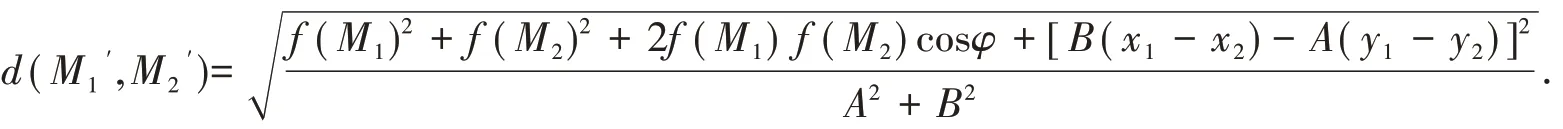
上式與文獻[4]導出的結果一致，對比可知用向量工具推導更為直接，應用范圍也更廣.

4 對角線向量定理與對棱角公式的統一證明

二面角問題的一個常見背景就是空間四面體. 四面體的六條邊中任意兩條之間的夾角余弦可通過計算對應兩向量的數量積求出，而任意兩邊對應向量的數量積均可由另外四邊的平方和與差表出，這就是在文獻[5]中被稱作的對角線向量定理與對棱角公式.

定理2 在四邊形ABCD 中，兩條對角線向量的數量積

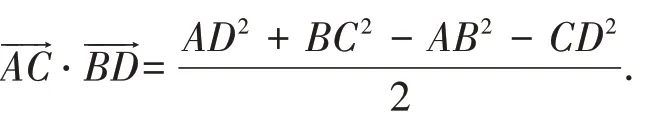
定理3 在四邊形ABCD 中，兩條對邊（棱）向量的數量積

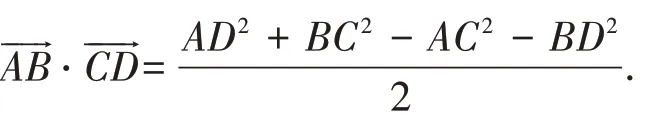
文獻[5]對這兩個定理在平面四邊形的情形分別給出了證明，同時指出在空間四面體（三棱錐）中結果也成立. 該文獻通過運用這兩個定理演示求解了多例立體幾何問題. 對于復雜的立體圖形包括動態翻折問題，將向量運算直接化為簡單的線段長度計算，要求的幾何量非常明確，極少依賴作輔助線，直觀明了，利用兩定理作出的解答都比較理想.

這里，我們指出這兩個定理的外在形式其實是統一的，即

按照上式表征的規則，這兩個定理非常容易記憶和使用. 無需圖示，下面僅運用向量的線性運算給出上面它們的統一證明，同時也說明：無論是空間四面體還是平面四邊形，公式都是一樣成立的.

證明：記A,B,C,D 為空間四面體（或平面四邊形）的四個無序頂點，O 為空間（或平面）內任一點. 則

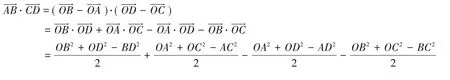
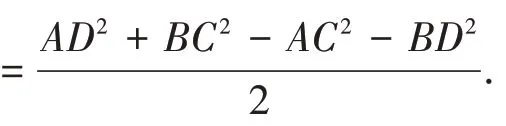
綜上，通過本文給出的向量在與二面角等相關問題中的應用，可以說明運用好向量的線性運算法則，在數量積運算性質的基礎上增加向量積這一工具，對求解包含二面角問題在內的空間解析幾何問題與立體幾何問題是有益的.