一種基于AP 的三支聚類改進算法

孫 暖，曹小平，劉 軍

（重慶科創職業學院 人工智能學院，重慶 永川 402160）

0 概述

聚類分析是數據挖掘的重要手段之一，聚類分析是把相似性大的對象歸為一類，同一類之間的相似度比較大，不同類之間的相似度越小越好，也就是說差異性越大越好，聚類技術現在已經廣泛應用于生物學、心理學、醫學地質學等各種領域。

Affinity Propagation 聚類算法又叫近鄰傳播算法，簡稱AP[1]，基本思想是基于因子圖的信念傳播和最大化算法。它根據N 個數據點之間的相似度進行聚類，這些相似度可以是對稱的（即兩個數據點互相之間的相似度一樣，如歐氏距離），也可以是不對稱的（即兩個數據點互相之間的相似度不等）。AP 算法不需要事先指定聚類數目，而是將所有的數據點都作為潛在的聚類中心，稱之為exemplar。但是AP 聚類對非團狀數據集的聚類效果并不好，因此許多專家學者對AP 算法進行了改進。如Li, Peixin，Gu, Wei 等將AP算法應用于光伏電站群建模[2]，提出了一種動態親和力傳播（DAP）聚類算法。然后，根據該算法的動態特性，對光伏集群中的光伏電站進行分組。最后，通過對同一組光伏電站的參數匯總和網絡簡化等效，得到光伏集群的動態等效模型。Liu, Zhihan[3]等將AP 算法應用于共享單車服務方面，提出了一種通過聚類確定倉庫位置的優化方法，利用AP 聚類算法的出租車OD 點，通過分析AP 聚類算法，對基于管理區域分割進行了分層優化，考慮出租車OD 點的稀疏相似度矩陣，對AP 聚類的輸入參數進行了調整。Guojun Gan[4]等在AP聚類算法中引入屬性權重，提出了一種子空間聚類算法，屬性權重的相對大小可用于標識嵌入集群的子空間。針對AP 聚類算法對流形數據集的聚類效果并不理想，本文提出利用類之間的緊致度來進行類的合并，對緊致度大于閾值的相鄰類采取合并措施，文本引入新的相似度矩，陣實驗表明合并后類的數量減少，聚類結果更加合理。

1 AP 聚類概述

相似度矩陣是AP 算法的基礎，相似度矩陣可以是對稱的，也可以是不對稱的，能否得到合適的相似度矩陣決定了聚類效果的優劣。本文利用無向加權圖，構造相似度矩陣Sij，將每個樣本看作無向圖的每個頂點來構建無向加權圖，構造公式如下：

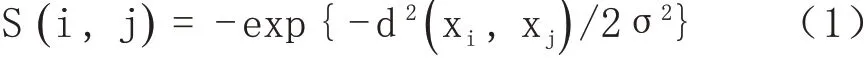
dij表示xi和xj的歐氏距離，σ 是平衡因子，

在相似度矩陣中，S (i , j )表示樣本j 多大程度上適合作為樣本i 所屬類的中心，對角線上的元素S ( )k , k 稱為偏向參數，S ( k , k )的值越大，則k 作為類代表點的可能性就越大。通常設定所有的偏向參數為p，聚類的數量受p 影響，若p 值為相似度中的最小值，則得到的聚類數最小，若p 為相似度的最大值則聚類數最多，得到的類數越多，通常取相似度均值作為p 值，計算公式為[5]：

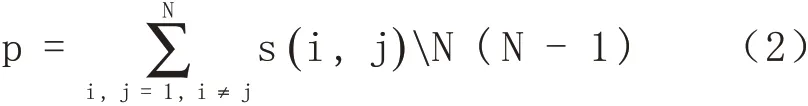
AP 算法中引入兩個信息參數，吸引度信息r (i , j )和歸屬度信息a ( i , j )，對任意樣本i，在其他樣本中選擇對其吸引度和歸屬度最大的樣本作為其類代表點，AP 算法的核心就是這兩個值的交替更新，為避免發生震蕩我們引入阻尼系數λ[6]，（取值為0.1），假設t 是當前迭代次數，更新公式為如下：

吸引度更新：

SAP-Algorithm 算法1

輸入：S 表示相似度矩陣，X 為數據集合，M 表示最大迭代次數，r(0), a(0)表示初始的吸引度和歸屬度，P 偏向參數，聚類中心集合V ={v1, v2, ..., vt}，計數器m

輸出：類別{v1, v2, ..., vt}

begin

①M=500，m=0，r(0)=0，a(0)=0，V = ?；

②P = p ( S ) //根據式（2）計算偏向參數；

③while m 〈 M do；

④for xk, xi∈X do；

⑤if makx { a (i , k ) + r (i , k )}do；

⑥v ←k; //xi類代表點是xk；

⑦m++；

⑧for others ( xi) do；

⑨v ←xi;///分配給各自的最優類代表點end；

算法分析：本算法在已知相似度矩陣的基礎上進行，由于相似度矩陣已經計算出，所以不必算相似度矩陣，算法在while 循環內，對元素xi，計算該元素與其他元素的吸引度與歸屬度的和，并求出最大值，找到該元素的類代表點。最后對于其他的元素分配給最大的類代表點。SAP 算法不需要事先指定聚類數目，將所有點作為聚類中心。盡管AP算法對一些結構簡單的數據其聚類效果好，但是對一些結構比較復雜（如非團狀）的數據集，它卻往往得不到很好的聚類效果。對于這一缺陷本文提出了基于ε 鄰域的類合并，其主要思想是將對象的ε 鄰域定義為結構算子，然后利用結構算子對SAP 算法s 的結果進行融合，合并原本屬于同一類的結果。

2 類的合并

定 義 1（ε 鄰 域 ） 設 數 據 集 U ={ x1, x2, …, xn} 中 ， xi∈U， 稱 Nε( )xi={y ∈U:d ( y , xi) ≤ε} 。

定 義 2（q 近 鄰 距 離 ） 設C = { c1, c2, …, ck}[8]，是DPC 算法的聚類結果，xe∈Ci(i = 1 , 2 , …, k )，QNN ( )xe是在Ci中距離xe的最近的q 個點的集合，xt∈QNN (xe)，稱為點xe的q 近鄰距離；為 類Ci的q 近鄰距離。

定 義 3相 鄰 類 對 于 類 Ci[9]，任 取xb∈Cj( i ≠j )，取ε = p ?avg ( Cj)，考慮xb的ε鄰域，若Nε( xb)?Ci≠?，則xb為臨界點。Ci與Cj屬于相鄰類。

類的合并,如果一個類中的元素的鄰域包含其他類中的元素，則此元素為該類的臨界點，我們可以根據臨界點與另外類的緊密聯系程度，來決定兩個類是否進行合并。對于相鄰類的臨界點我們采取的策略是：對于相鄰類計算兩個相鄰類的類臨界點之間的緊致度Tij，計算公式如下：

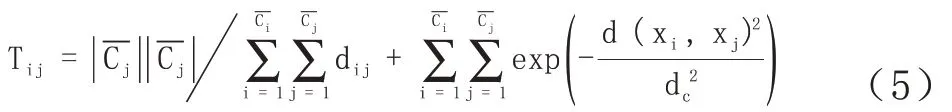
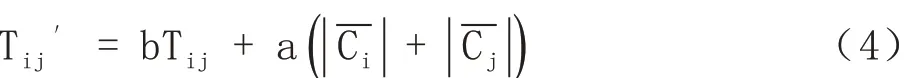
SAP-Algorithm 算法2

輸入：聚類的結果C = {c1, c2, …, ck}，臨界閾值α。

輸出類簇:合并后的類C = {c1, c2, …, cm}。

①根據定義3 求出相鄰類（如Ci和Cj相鄰，則Ci，Cj是相鄰類）；

②如果相鄰類的Tij′大于閾值α,則對兩個類進行合并，否則不進行合并；

③ 重 新 輸 出 新 的 聚 類 結 果 C ={c1, c2, …, cm}；

上述算法是基于算法一的聚類結果的基礎上；利用T′ij對類進行合并，算法二只計算類的臨界點集合，并不是計算類的所有點，大大的降低算法的時間復雜度，提高了算法的效率。

3 實驗

本節通過實驗對所提的算法進行性能分析，本文算法的思想為：通過AP 聚類算法得到初始的類簇中心點和初始類，使得初始化聚類中心和類簇得到確定，由于類的個數自動生成，有時可能會產生過多的類別個數，其中一些類可以合并，聚類結果不準確所以用類的相異度計算確定需要合并的類。仿真環境：軟件Python3.8，操作系統win10 64 位，硬件CPU2.0GHz，內存8GB，硬盤500G。

用自定義數據集進行聚類，該數據集為流形數據集，共兩類，使用原始的AP 算法得到的結果分成四類，因為原始AP 基于歐氏距離對環形數據集的效果并不理想。為了解決這種問題，我們把相似度較高的類別重新結合在一起，便會得到更好的聚類結果，采用類與類之間的合并來處理這種情況。

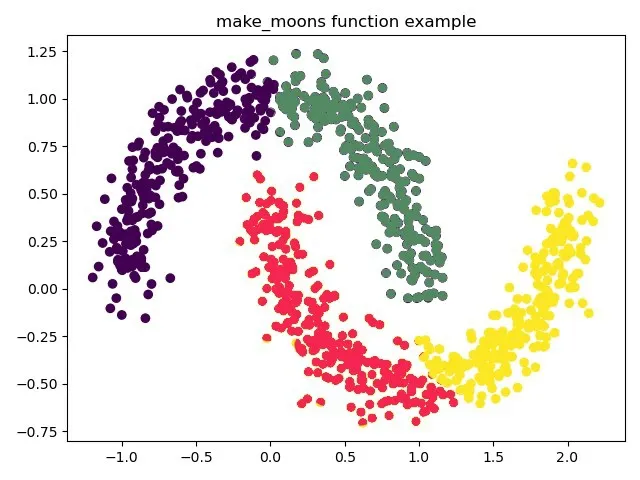
圖1 AP 算法的聚類結果

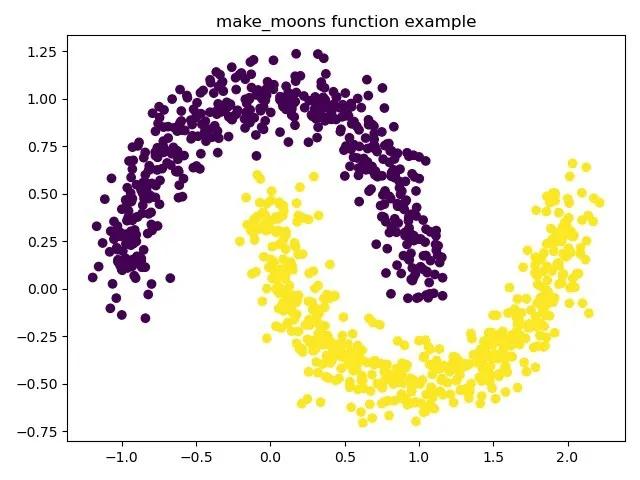
圖2 SAP 算法的額聚類結果

圖2 我們得到的最終聚類結果，已經成功的把許多能合并的類別合并在一起，把原本誤分的類已經合并，合并之后的聚類結果比較合理，從圖中清楚的看到分為兩類。

接下來對環形數據集分別用K-means 和SAP進行對比實驗，圖三是對Kmeans 的聚類結果，該算法把環形數據集分成四部分，聚類的結果數目并不準確，圖4 是SPA 算法的聚類結果，該結果很好的把環形數據集分為兩類，內環和外環，相比K-means 聚類結果更加準確。

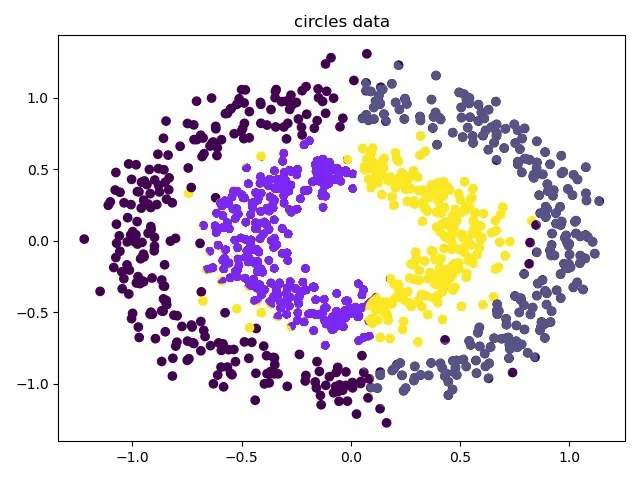
圖3 k-means 算法的聚類結果

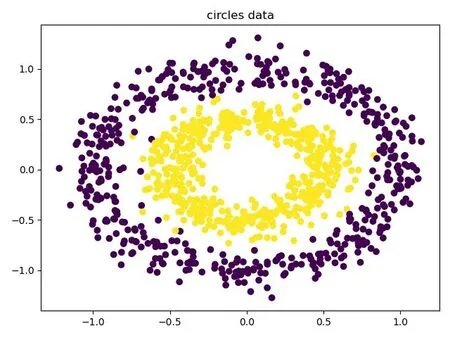
圖4 SAP 算法的額聚類結果

為了準確的描述聚類的結果優劣，引入以下三個指標評價聚類結果的優劣Purity 評價法[10～13]、RI 評價法、F 值評價法、ACC 我們用這四個指標來衡量算法的準確度和精度，求得四個指標的均值和標準差。把AP 算法、K-means 算法[14]，DBSCAN 算法[15]、SAP 算法進行對比。從表1 可以看出，K-means 和原始AP 聚類算法采用的是歐氏距離作為度量，所以對這種流形數據集聚類的數目多于實際的聚類數目，而DBSCN 是基于密度的聚類，得到的類別數正確，但是在ACC、Purity、RI、F 方面指標不如SAP，因為SAP 對相似度矩陣進行了改進，并且對能合并的類進行了合并，綜上所述，SAP 算法要優于其他幾種算法。

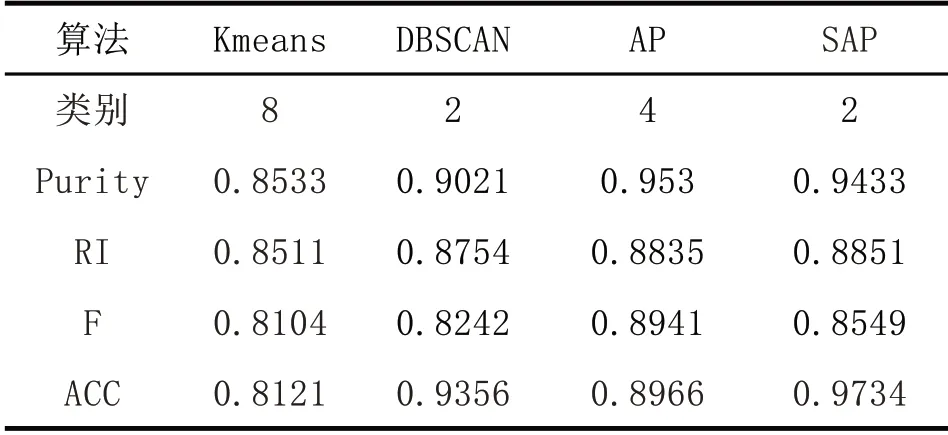
表1 算法對比

接下來采用UCI 數據集中的準確率對比實驗，本文對上述四個算法進行準確率對比實驗，在UCI 數據集上進行實驗，結果如表2 所示，從表中可以看出，SPA 算法在所有的數據集上的聚類準確率明顯高于其他的三個算法。因為本文采取類與類之間的緊致度，進行了類的合并，例如，Iris 有三個類，其中兩個類之間有交叉，采用本文的方法可以有效解決這種情況。

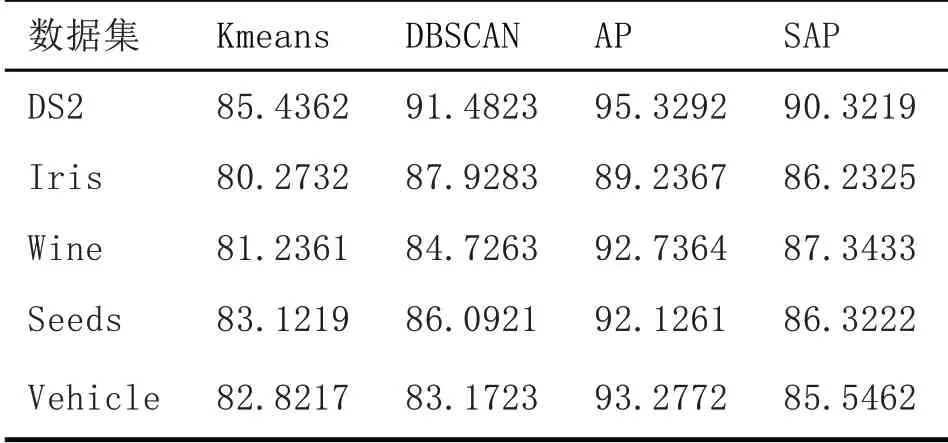
表2 準確率對比試驗（%）

表3 是對時間耗時方面的分析，從中可以看到AP 和K-means 耗時比SPA 要少，因為原始算法不需要進行類的合并等所以時間最少，但是本文的算法采用了只對臨界的集合進行計算，因此時間耗時并沒有相差很大，而DBSAN 算法由于對整個數據集進行計算所以時間的相對與本文算法來說很高，綜上所述本文的算法在精確度上比其他算法要高，耗時也是本文算法的優點。

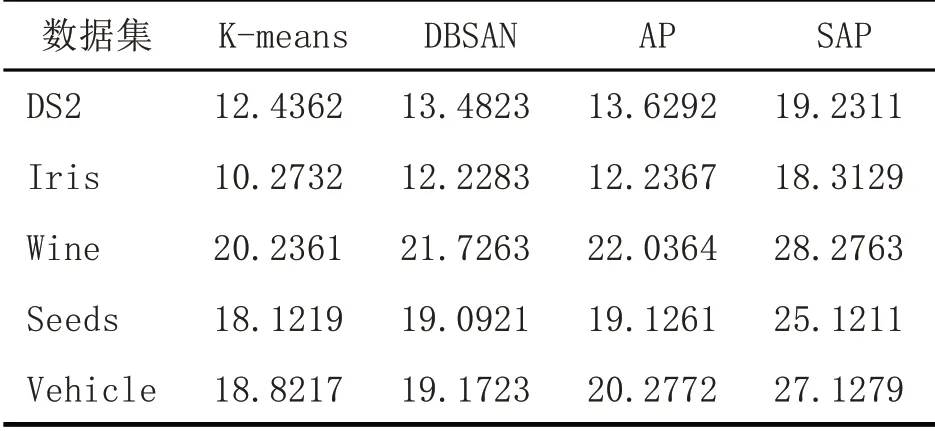
表3 時間對比試驗（s）

4 結束語

本文在針對AP 聚類算法不能對流形數據集進行聚類，采用一種基于無向加權圖的相似度矩陣，并且提出類與類之間緊致度的概念，對大于閾值的類進行合并，試驗結果表明，不管在時間復雜度還是準確率方面，本文的算法都有優勢。由于不同的數據集閾值不同，后續研究的重點是對閾值的選取進行研究。