衛星與雷達位置數據自適應關聯
熊振宇, 崔亞奇, 熊 偉, 顧祥岐
(海軍航空大學信息融合研究所, 山東 煙臺 264001)
0 引 言
隨著監視技術的不斷發展,對目標的探測手段日益增多,探測能力逐步增強。然而不同探測手段所獲取的數據間差異不斷增大,對于當前有限的關聯融合能力,不僅沒有提升整體的監視能力,還導致了更多問題。多源數據關聯主要用于判斷對同一目標描述的一致性[1],是多源數據融合的前提和基礎,在軍事和民用領域都有廣泛的應用[2-5]。例如目標識別、海洋監視、目標跟蹤、環境監測等。本文主要研究衛星和雷達位置數據間的關聯問題。衛星探測范圍廣、重訪周期長、定位精度差,一般在監視過程中用于大范圍探測[6];雷達探測范圍小,更新周期短,定位精度高,一般在監視過程中用于目標的連續跟蹤監視[7]。衛星與雷達之間的關聯可以將兩者的信息有效綜合起來,互補兩類信息各自的不足,實現目標的完全掌握。為有效綜合集成空間信息網絡中的多源信息,形成多手段聯合的預警探測體系,大差異多源信息關聯是最亟待突破的難題[8-10]。
為解決多源數據關聯問題,文獻[11-13]以雷達與無源雷達兩種手段間關聯為背景,解決雷達信息與定位精度差的無源雷達信息間的關聯問題。文獻[14]利用傳統方法提取出艦船目標的拓撲結構特征和屬性特征,同時引入了Dempster-Shafer(簡稱為DS)證據理論[15]解決了成像遙感信息和衛星電子信息間的艦船目標關聯問題。文獻[16]采用相干點集(coherent point set, CPS)分析法建立多模態融合模型,利用成像遙感信息和衛星電子信息中目標的位置坐標和屬性特征實現關聯匹配。文獻[17]將高斯混合模型(Gaussian mixture model, GMM)[18]和一致性漂移算法(coherent point drift, CPD)[19]相結合,提出了非均勻GMM(inhomogeneous GMM, IGMM),采用期望最大值(expectation maximum, EM)[20]計算關聯匹配結果。以上解決多源數據關聯問題都采用了迭代優化的傳統關聯方法,存在的主要缺點有:關聯成功率低、泛化能力弱、適用范圍有限、關聯速度慢、人工干預強等問題。同時上述關聯方法僅解決了形式簡單、條件理想情況下的關聯問題,而對于雷達和衛星圖像此類更一般、更實際、更具代表性的關聯問題缺乏研究。
針對上述問題,本文提出了一種衛星與雷達位置數據自適應關聯模型。首先基于多層神經網絡(multi-layer neural network, MLN)搭建整體差異參數提取網絡,分別提取衛星目標點和雷達目標點的整體差異參數。接著采用串聯等方式整合提取到的差異參數得到全局差異參數。然后將全局參數通過設計的位移變換網絡實現兩類信源目標的配準對齊。最后根據定義的關聯判別準則對配準后的目標點進行關聯判斷。仿真實驗結果表明,該模型能夠很好地適應隊形變換、定位出差、虛警漏報等場景,有效提高了關聯速度和精度。
1 問題描述
假設同一時刻衛星在某一區域內探測到目標點位置集合為S,雷達探測到目標點位置集合為G。由于雷達探測較為連續,可以雷達為參考,衛星向雷達進行關聯。實測數據分析發現,衛星量測與雷達量測間受時間間隔和定位誤差的影響產生較大的空間差異。其中受時間間隔影響,目標點位置的整體差異具有一致性,同時每個點受定位誤差的影響,目標點之間的差異還具有個體波動性。因此,雷達與衛星量測點關聯問題可描述為
(1)

2 模型設計
衛星與雷達探測的目標點空間差異性大,難以直接進行關聯匹配,需對兩種信源中每個目標點先配準對齊,再關聯判斷,同時空間差異函數ο(·)的優化不受映射函數m的影響,而映射函數m取決于空間差異函數ο(·)的優化程度。所以采取先優化空間差異函數ο(xs(i),λ),后優化映射函數m(i)的思路設計模型。
(1) 對于優化ο(xs(i),λ),采取先整體后個體的方式進行模型設計,網絡模型如圖1所示。

圖1 網絡模型
衛星目標點xs(i)通過位移變換Γ能夠逼近對應關聯的雷達目標點xr(m(i))。衛星目標點xs(i)的變換過程為
Γ(xs(i),o)=xs(i)+o(xs(i),λ)
(2)
首先利用神經網絡強大的信息提取能力,采用MLN和最大池化函數提取衛星和雷達目標點的整體差異參數λ。再利用神經網絡強大的函數逼近能力,將整體差異參數λ與衛星目標點集S串聯整合后通過多層神經網絡估計衛星目標點到雷達目標點的位移變換ο(xs(i),λ)。
(2) 對于優化映射函數m(i),通過先計算關聯矩陣再采用最大關聯系數法配對實現每個雷達目標點和位移后的衛星目標點間的關聯。
2.1 整體差異參數提取
時間間隔導致衛星與雷達目標點的空間差異具有一致性,設計整體差異參數提取網絡提取出目標點顯著性的差異特征。整體差異參數提取網絡如圖2所示。
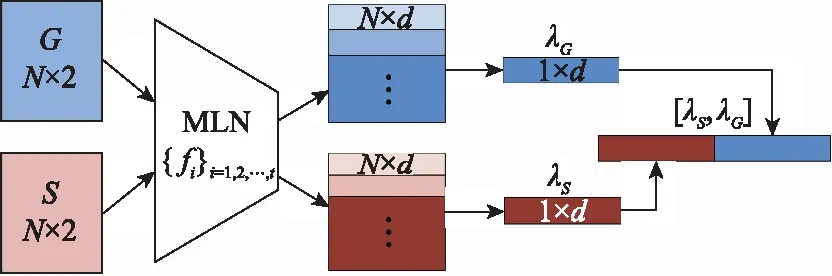
圖2 整體差異參數提取網絡
首先,將衛星和雷達目標點集合D={(S,G)|S,G?R2}作為網絡的輸入部分,該網絡采用了含有Relu激活函數的多層神經網絡:{fi}i=1,2,…,t,其中t為網絡的層數,然后將網絡的輸出通過最大池化函數進行歸一化處理,提取到整體差異參數λ={(λS,λG)|λS,λG?Rd},其中d為參數的維度,最后將提取到的差異參數串聯[λS,λG]。整體差異參數提取網絡結構如表1所示。該網絡的表達式為
λS=Maxpool{ftft-1…f1(xs(i))}xs(i)∈S
(3)
λG=Maxpool{ftft-1…f1(xr(j))}xr(j)∈G
(4)

表1 整體差異參數提取網絡結構
該網絡采用了5層MLN結構,即t=5,網絡輸出的維度為512維,即d=512。其中,M為訓練過程中每一批次數據的大小。
2.2 位移變換估計
在位移變換的過程中,通過第2.1節所提網絡不僅能夠讓衛星數據中的目標和雷達數據中的目標盡可能重合,同時還能保證位移變換函數連續且平滑。位移變換估計網絡如圖3所示。
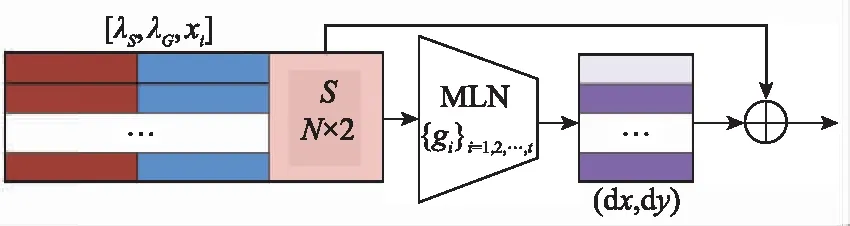
圖3 位移變換估計網絡
首先將串聯后的整體差異參數[λS,λG]復制N次,目的是讓復制后的維度與衛星數據的維度相同;然后將衛星數據與復制后的差異參數串聯得到全局差異參數[λS,λG,xs(i)];最后將全局差異參數作為輸入通過帶有Relu激活函數的多層神經網絡:{gi}i=1,2,…,s中,所以空間差異函數為o=gsgs-1…g1。位移變換估計網絡的表達式為
dxs(i)=gsgs-1…g1([λS,λG,xs(i)])
(5)
(6)


表2 位移變換估計網絡結構
考慮到衛星數據與雷達數據中每個目標點都存在對應關系,采用倒角距離[21]進行度量。為了讓衛星數據的目標點經位移變換后與雷達數據的目標點距離接近,該模型的損失函數倒角損失定義如下:
(7)
式中,θ為該關聯網絡模型中需要訓練的參數;β為超參數,在實驗中β=0.1。
2.3 關聯判決
(8)

基于以上原則采用最大關聯系數法進行關聯判斷,具體過程如下:

(2) 然后,從關聯系數矩陣C(i,j)中刪除最大元素cij所對應的行和列元素,得到新的降階關聯矩陣C1(i,j),但原矩陣的行、列號(即數據中對應的目標)保持不變,從降階矩陣C1(i,j)中找到新的最大值以判定該下標對應目標的關聯;
(3) 重復上述過程直到求出降階關聯矩陣CN-1(i,j)中的最大元素。
3 仿真分析
為充分驗證自適應關聯模型算法的有效性,分別進行數據集構建、仿真場景驗證和對比實驗。根據實際情況,在仿真實驗中考慮了4種仿真場景,分別驗證所提模型算法在處理艦船編隊隊形變換、定位誤差、虛警、漏檢等情況時的適應能力。在對比試驗中,將傳統GMM算法與本文模型算法進行對比。仿真場景驗證和對比實驗都采用了20 000組訓練集和20 000組測試集。整個實驗是在Tensorflow框架下的一個64位工作站上進行的,該工作站主要配置為Ubuntu 16.04、32gb RAM、8intel(R)Core(TM)i7-6770kcpu和NVIDIA GTX 1080Ti×2。
3.1 數據集構建
根據艦船編隊實際場景,首先構建訓練數據集。衛星數據的生成是通過對某一單元區域內隨機選取11個目標點(即N=11)。假設雷達上報數據時間晚于衛星上報數據時間,將衛星數據進行平移得到雷達數據,在平移過程中涉及的參數有x坐標軸平移量Δx∈[-5,5],y坐標軸平移量Δy∈[-5,5]。考慮到艦船的隊形可能發生變化,即雷達數據中的位置坐標點發生了非剛性形變,引入形變因子l。
測試數據集的構建大致與訓練數據相同。主要考慮以下4種場景。
(1) 仿真場景1:考慮到兩種觀測手段存在時間間隔。在此期間,艦船編隊發生位移和隊形變化,即雷達數據相對于衛星數據發生平移和非剛性形變,具體參數設置與訓練集構建相同。
(2) 仿真場景2:考慮到兩種觀測手段所獲取的數據在定位精度上存在偏差。在場景1基礎上對雷達數據G中的每個位置坐標點添加位置噪聲。位置噪聲采用均值unoise=0,標準差σnoise=f的高斯噪聲,其中f為噪聲因子。
(3) 仿真場景3:考慮到獲取的數據可能存在虛警點,在場景2基礎上對雷達目標點集合G中添加N×r個出格點,其中r為出格點比率。
(4) 仿真場景4:考慮到獲取的數據可能存在漏警點,在場景2基礎上對雷達目標點集合G中減少N×s個缺失點,其中s為缺失點比率。
3.2 仿真場景驗證
(1) 仿真場景1
假設雷達和衛星檢測概率為100%,即不存在虛警和漏警點。雷達數據的獲取時刻晚于衛星數據的獲取時刻,在這段時間內艦船編隊發生機動,隊形產生形變。通過增加形變因子l的值,驗證模型對艦船編隊發生隊形變化的適應能力。l越大則雷達數據目標點發生非剛性形變的形變量越大,實驗結果如圖4所示。第1列表示訓練前衛星和雷達目標點的位置關系,其中紅色代表衛星探測到的目標點,而藍色代表雷達探測到的目標點。第2列表示位移變換時每個衛星目標點的移動軌跡。第3列表示經過目標點位移變換后衛星數據與雷達數據的目標點位置關系。實驗分別測試了l分別取0.3、0.9和1.5時的匹配效果。

圖4 仿真場景1的關聯結果
實驗結果表明,形變因子較小時匹配結果精確,有相同標號的點幾乎完全重合;隨著形變因子增大,雷達目標的整體編隊結構產生劇烈變化,加大了匹配難度。從最終匹配結果可以看出,雖然部分點沒有完全重合,但有相同標號的點距離更近。根據第2.3節中定義的關聯判別準則計算,l分別取0.3、0.9和1.5時的關聯準確率分別為100%、81%、64%。
(2) 仿真場景2
假設雷達和衛星數據不存在虛警和漏警點。雷達數據的獲取時刻晚于衛星數據的獲取時刻,在這段時間內艦船編隊發生機動,隊形產生形變,形變因子l=0.3。通過增加噪聲因子f的值,驗證模型的抗噪聲能力。實驗結果如圖5所示,實驗分別測試了f分別取0.1、0.3和0.5時的匹配效果。

圖5 仿真場景2的關聯結果
實驗結果表明,噪聲因子較小時,經過目標點位移變換后的衛星數據與雷達數據目標點匹配結果精確,重合度高。當噪聲因子增大,雷達目標點的相對位置發生較大改變時,通過本文提出的自適應關聯模型后,衛星數據與雷達數據目標點匹配結果較差,但單純依靠位置信息,人眼難以判別。根據第2.3節中定義的關聯判別準則計算,f分別取0.05、0.1和0.2時的關聯準確率分別為100%、64%、36%。
(3) 仿真場景3
假設雷達數據存在虛警,在雷達數據中添加額外的出格點,虛警率用出格點比率表示。雷達數據的獲取時刻晚于衛星數據的獲取時刻,在這段時間內艦船編隊發生機動,隊形產生形變,形變因子l=0.3,噪聲因子f=0.05。通過增加出格點比率r的值,驗證模型的抗虛警能力。實驗結果如圖6所示,實驗分別測試了r分別取0.09、0.27和0.45時的目標匹配效果。
實驗結果表明,當出格點的個數較少時,提出的模型結構能夠很好地忽略掉出格點,保持衛星數據和雷達數據目標點間的匹配;當出格點個數較多時,與密集出格點臨近的目標在匹配時受到影響,發生錯匹配,但離出格點較遠的目標依然能夠保持很好的局部完整性,匹配結果精確。根據第2.3節中定義的關聯判別準則計算,r分別取0.09、0.27和0.45時的關聯準確率分別為100%、64%、55%。
(4) 仿真場景4
假設雷達數據存在漏警,隨機刪除雷達數據中的目標點作為缺失點,漏警率用缺失點比率表示。雷達數據的獲取時刻晚與衛星數據的獲取時刻,在這段時間內艦船編隊發生機動,隊形產生形變,形變因子l=0.3,噪聲因子f=0.05。通過缺失點比率s的值,驗證模型的抗漏警能力。實驗結果如圖7所示,實驗分別測試了s分別取0.09、0.27和0.45時的目標匹配效果。

圖6 仿真場景3的關聯結果

圖7 仿真場景4的關聯結果
實驗結果表明,缺失點個數較小時,能夠保持雷達數據中編隊目標的整體輪廓,匹配結果精確;當缺失點個數較多時,只能保持編隊目標的局部輪廓,部分局部點匹配正確。根據第2.3節中定義的關聯判別準則計算,s分別取0.09、0.27和0.45時的關聯準確率分別為90%、75%、67%。
3.3 對比試驗
與現有的傳統關聯模型不同,本文提出一種學習型的自適應關聯模型,為了驗證該模型的泛化能力和關聯效率,與GMM進行對比時主要考慮關聯耗時和平均關聯準確率兩項指標。
根據本文模擬的4種仿真場景,計算不同條件下模型在測試集中的平均關聯準確率,實驗結果如圖8所示。

圖8 與GMM算法實驗結果對比
在圖8(a)中,當雷達目標點發生非剛性變換,本文算法相比于GMM算法適應能力更強。當形變因子小于0.6時,本文算法的平均關聯準確率在90%以上,而GMM算法的最高平均關聯準確率不到90%。隨著形變程度的增加,本文算法的準確率緩慢下降,而GMM算法下降較快,無法應對較大的非剛性形變。當形變因子達到2.0時,本文算法準確率依然能夠達到50%以上,而GMM算法準確率不到30%,難以進行關聯。
在圖8(b)中,隨著噪聲因子的增加,兩種算法的準確率都下降較快,難以克服高噪聲的情況,但本文算法的關聯準確率整體優于GMM算法。在圖8(c)和圖8(d)中,本文算法在應對出格點和失格點的情況明顯優于GMM算法,當出格點個數較少時,關聯準確率較于GMM算法提升較大,表明本文算法不僅能夠實現目標點的全局關聯,對局部目標點依然能夠保持很好關聯效果。
根據仿真場景1中的參數設置,對比本文算法和GMM算法在形變因子為0.9時的平均關聯準確率和關聯時間,實驗結果如表3所示。
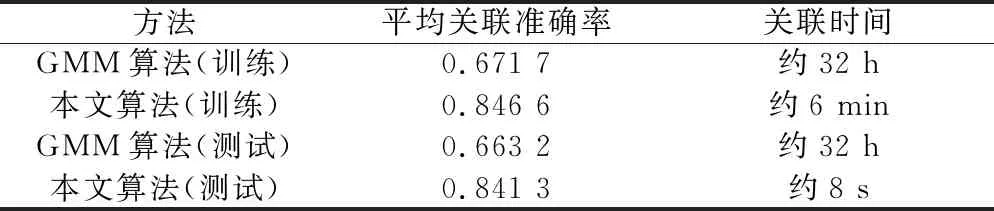
表3 與GMM算法的性能和時間對比
實驗結果表明,本文算法在平均關聯準確率和關聯時間上明顯優于GMM算法,表現出很好的關聯精度和效率。這主要因為傳統的GMM算法采用迭代優化的策略,不同場景中每一次關聯過程都是相互獨立的,極大程度上限制了該算法在應對大規模關聯任務時的有效性。而本文算法采用基于學習的策略,能夠通過神經網絡進行離線訓練,同時學習到目標點的全局和局部特征,在測試時關聯精度高,耗時少,能夠實時處理大規模的關聯任務。
4 結 論
本文提出了衛星和雷達的位置數據關聯新問題,基于神經網絡設計了一種自適應的關聯算法模型,根據實際情況構建基于位置信息的衛星和雷達關聯數據集。仿真結果表明:該算法關聯速度快,精度高,能夠適用于大規模數據下的跨源關聯任務,并且在應對隊形變換、定位誤差、虛警漏報等情況適應能力強,即使出現整體編隊形狀變化大到人工難以關聯判斷的程度,所提算法也能給出正確有效的關聯結果。
為進一步提高跨源關聯準確率,應對大形變、高噪聲等惡劣場景,下一步將采用衛星和雷達的位置數據和特征數據相結合的方式解決兩者之間的關聯問題,進一步提高跨源關聯效率和準確率。

