無動力船舶錨泊防臺抗風能力研究
◎ 王艷杰 交通運輸部水運科學研究院
無自航能力的駁船、打樁船、海上生活支持船和工程支持船等無動力船舶,避風過程中一旦走錨,無法動車進行抗風、頂浪等操作,可能隨風漂移,從而威脅周圍船舶、人員以及周邊水域的安全,其防臺問題至關重要。
船舶的抗風能力大小是防臺安全的決定性因素,確定其抗風等級是防臺安全的前提條件。
1.穩性衡準與船舶抗風能力
現行的船舶穩性衡準采用“確定性力學分析法”,先把船舶傾覆的物理因素簡化為數學模型,通過解析計算,對船舶穩性作出定量評估。上述過程沒有直接反映出風級風速的概念,但經過風壓換算可以求出風速,即抗風能力,公式如下:
船舶抗風等級:
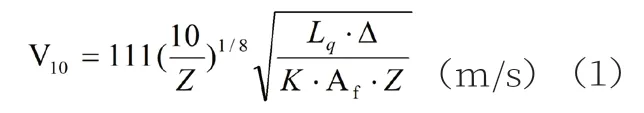
船舶最大抗風等級:
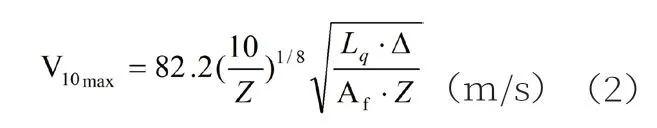
式中:V10—風壓作用力臂10m高處的風速;Z—受風面積中心距水面距離,m;Lq—最小傾覆力臂,m;△—排水量,t;K—穩性橫準值;Af—受風面積,m2。
2.基于船舶運動規律的抗風能力計算模型
一定載重狀態下的無動力船舶,按一定錨泊方式錨泊防臺時,船體受到的力主要為風力Fa、水動力Fw、錨鏈及錨抓力即錨泊力p。在不走錨的前提下,出一定鏈長時可抵御的船舶可受最大水平外力,稱為船舶在該條件下的臨界錨泊力。當錨泊力達到臨界錨泊力時,船舶所承受的風力最大。此時,船舶受力滿足如下條件:

式中:n—船舶實際錨泊狀態下產生的錨泊力/單錨泊產生的錨泊力。
單錨泊狀態下臨界錨泊力prmax(t)可以通過下式計算:
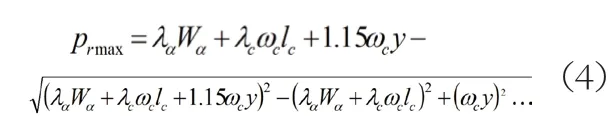
式中:λα—錨抓力系數;λc—錨鏈抓力系數;Wα—錨重,t;ωc—每米錨鏈重量,t/m;lc—出鏈長度,m;y—海底至錨鏈孔垂直距離,m。
船舶所受風力Fa(N)可通過下式計算:
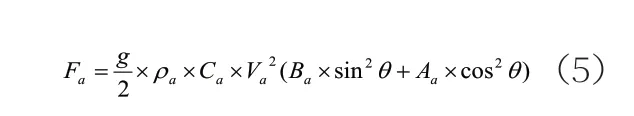
式中:ρa—空氣密度;Ca—風動力系數;Va—相對風速,m/s;Aa—水線以上船體正面投影面積,m2;Ba—水線以上船體側面投影面積,m2;θ—相對風舷角。
船舶所受的水動力Fw(N)可通過下式計算:
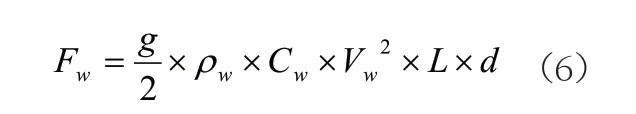
式中:ρw—水密度;CW—水動力系數;VW—船舶與水的相對速度,m/s;L—船舶水線長,m;d—船舶吃水,m。
將式(4~6)代入式(3),單位化為統一,可以反推出船舶臨界狀態下所受風力Vαmax(m/s)大小,即船舶能抵抗的最大風力:
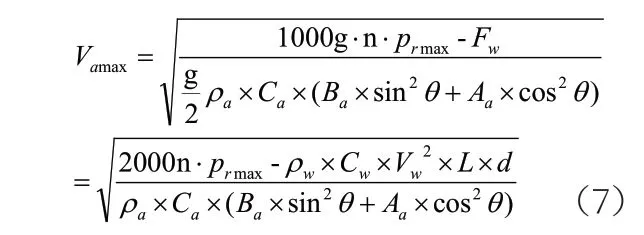
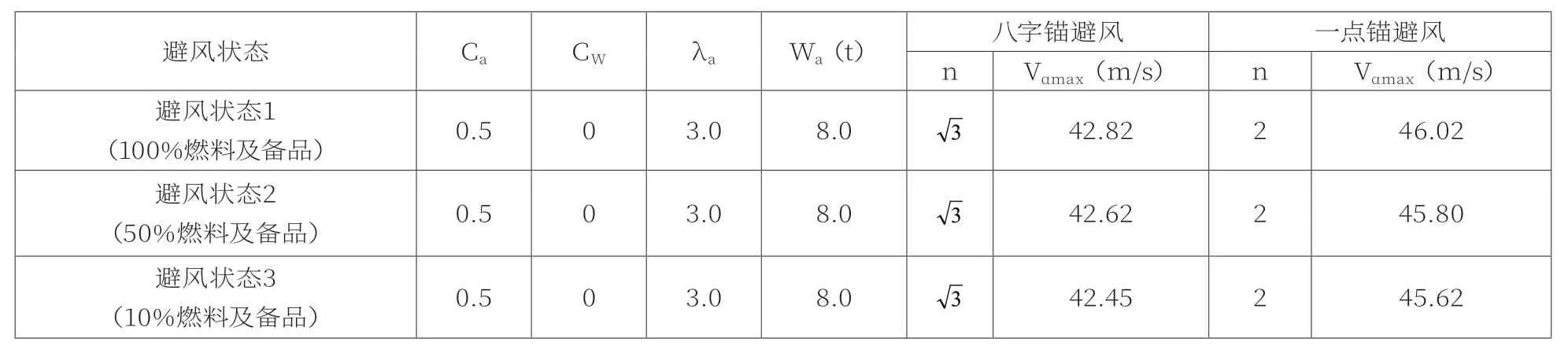
表1 施工船抗風能力(基于船舶運動規律)
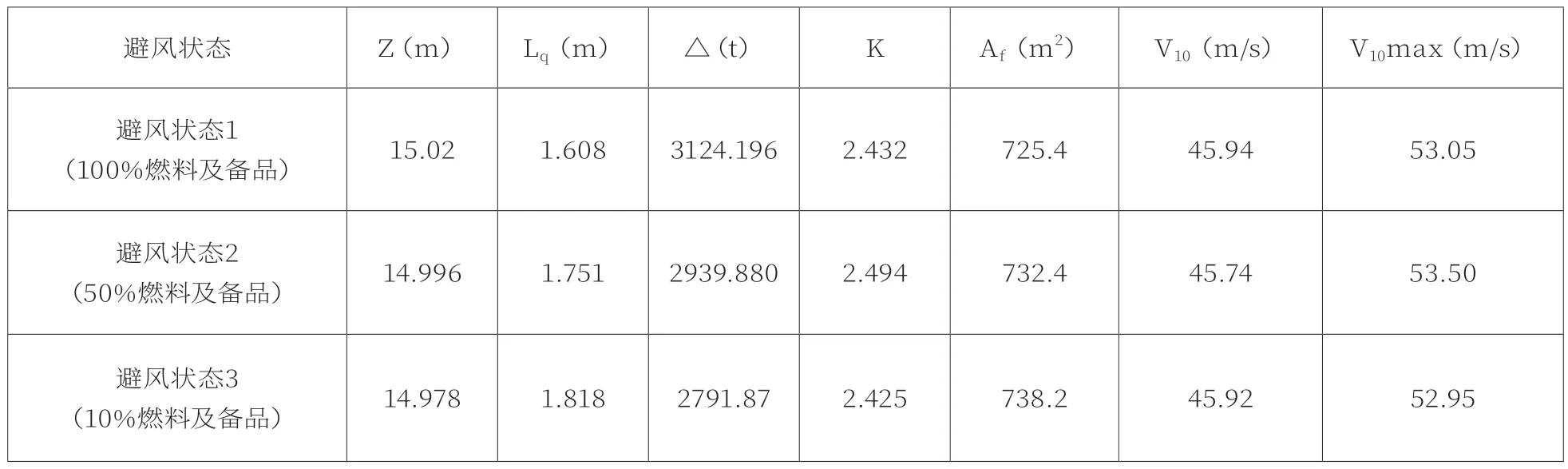
表2 施工船抗風能力(基于穩性衡準)
3.計算實例
珠江口水域是我國水上運輸最為活躍的地區之一,也是受臺風侵襲較多的地區之一。“砂樁3號”無動力施工船參與港珠澳大橋建設期間,推薦防臺水域底質為泥沙和沙泥,防臺時拋八字錨或一點錨。根據式(7)計算其不同避風狀態下抗風能力大小,如表1所示。
風壓換算后可知,八字錨避風時,避風狀態1和2情形下抗風等級均為10級陣風,避風狀態3情形下為9級陣風;一點錨避風時,在3種避風狀態下抗風等級均為10級陣風。
而基于穩性衡準轉換得到結果為:“砂樁3號”施工船在3種避風狀態下抗風等級均為10級陣風,最大抗風等級均為12級陣風,如表2所示。
基于船舶運動規律得到的抗風能力較基于穩性衡準得到的抗風能力低,且不同的避風狀態下抗風能力有一定的差別,在實際運用中偏安全一些。
4.結論
本文提出的基于船舶運動規律的抗風能力計算模型,可以實現對無動力船舶不同避風狀態、不同錨泊方式下抗風能力的估算,為駕引人員制定防臺方案提供參考。
船舶實際抗風過程中,其外部環境及制約因素十分復雜,各個制約因素之間的關系也是非線性的,抗風能力的量化是一個復雜問題。本文在計算模型建立過程中考慮到的因素可能與船舶實際抗風狀態受力情況等有出入。駕引人員在實際操作過程中,可以此為參考,結合船舶相關參數、實際避風經驗、相關主管部門的規章制度或指示等,制定合理可行的船舶避風方案。

