基于攝動落點預測與修正比例導引的復合修正算法設計

柯知非,高 敏,王 毅,宋衛東

(1.北京跟蹤與通信技術研究所,北京 100094;2.陸軍工程大學 導彈工程系,河北 石家莊 050003)

修正控制算法是指彈丸在飛行過程中所需遵循的規律,它的性能直接關系到彈丸命中目標的精度。對于二維彈道修正,適用于旋轉穩定彈的修正控制算法可大致分為方案控制算法與導引控制算法。方案控制算法可分為彈道成形(trajectory shaping)、預測控制(predictive control)、彈道跟蹤(trajectory tracking)3種,而適用于修正能力有限的彈道修正彈丸的修正控制算法僅有后兩種[1]。

JITPRAPHAI等[2]在基于脈沖修正的火箭彈上,研究了TT制導、PNG制導和PAPNG制導,通過仿真對比各方案的修正效能,文獻[3]研究了落點預測法和修正比例導引法,得出利用落點預測法進行制導的關鍵:通過實時預測落點位置計算零效脫靶量(ZEM)。

以上各種方案中,彈道追蹤法對彈載計算機的計算性能要求不高,相對而言是較為容易實現的[4]。文獻[5]采用該導引律對155 mm榴彈的操縱性進行了分析。然而,該方法未考慮修正控制過程中彈丸的速度信息,彈丸沿基準彈道的不斷穿越使修正控制的總能量產生大量消耗。何光林等[6]最早針對一維修正彈落點預報原理,對采用正交多項式擬合彈道和誤差補償的方法降低預報落點的偏差等進行了研究,為研究其他修正方式和二維彈道修正彈的落點預測方法提供了借鑒。黎海青等[7]針對固定翼控制的雙旋結構旋轉穩定彈,建立了七自由度運動方程,利用四自由度(4D)質點彈道模型設計了落點預測制導律,將該制導律用于旋轉穩定彈修正控制,大幅減小了落點散布。文獻[8]通過直線外推落點和帶重力補償直線的方法對脈沖末修迫彈進行脫靶量預測研究,進一步提高了落點外推算法的精度。田再克等研究分析了攝動理論落點預測在彈道修正彈上的應用[9-13],該理論在滿足彈道修正實時性要求的基礎上能較好地提高射擊精度與減小落點散布。楊泗智等[14]在高旋火箭彈平臺上利用了落點預測法進行彈道修正,該方法能有效地減小落點的圓概率誤差(CEP),但受于炮彈引信修正能力的限制,需要做進一步的優化。王鈺等[15]通過綜合攝動理論落點預測法與修正質點彈道預測法計算速度與精度的特點,提出了結合兩種方法的分段預測法,通過仿真得出了優于單一預測方法的結論。文獻[4]在雙旋彈上通過對比修正比例導引法和彈道追蹤法,研究得出修正比例導引在橫向上的修正效果更易受到測量誤差的影響,但其所需存取信息更少,修正比例導引相對優于彈道追蹤法,但彈道追蹤法的準確度相對更高。

本文在前人研究的基礎上,針對裝有基于固定鴨舵式二維修正組件的旋轉穩定彈,提出一種在彈道上升段采用攝動落點預測,下降段采取變系數修正比例導引的復合導引律,該算法綜合了2種方法的優點,既實現上升段的修正控制,又可以實現降弧段對目標點的閉合,提高了射擊精度。

1 修正控制特性

如圖1所示,固定鴨舵式二維彈道修正組件由一對相同舵偏角的反向減旋舵與一對相同舵偏角的同向控制舵組成,為單通道控制。由于組件的舵偏角固定,彈丸在飛行時通過控制修正組件同向舵的相對于地面的滾轉角實現彈道修正。

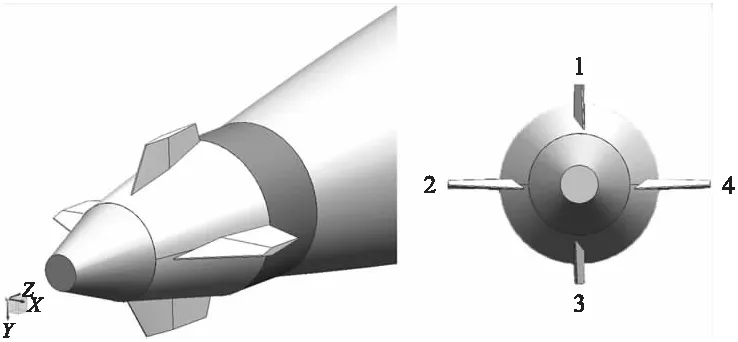
圖1 固定鴨舵式二維彈道修正組件外形示意圖

文獻[16]對修正彈偏流特性的研究發現:由于陀螺效應,彈軸將運動到控制角的反方向右側,即獲得與控制角方向相反的動力平衡角和垂直該平面向右的動力平衡角,并獲得相應的彈道修正量。即彈道的修正控制量相對于控制角存在一定的相位滯后,該相位滯后影響著控制信號的生成。不同發射初速、射角、修正持續時間、滾轉角對相位滯后存在一定影響[17],本文所涉及修正彈在對應裝藥的初速和射角上較為固定,受以上因素影響較小,故對以上項目統一進行擬合。

該滯后角與彈丸飛行馬赫數成一定關系,通過多項式擬合得出:

φz=-285Ma4+1 638Ma3-3 517Ma2+3 352Ma-1 032

(1)

式中:φz為滯后相位角,Ma為馬赫數。

2 修正算法設計

2.1 攝動落點偏差預測

假定X0(x0,y0,z0)和XT(xT,yT,zT)分別為發射系中發射點和目標點坐標。若彈丸初速和射角一定,則在不加入任何干擾的情況下命中目標點的彈道曲線是唯一的,該彈道即為基準彈道。然而,彈丸飛行過程中,由于彈丸自身參數偏差、氣動參數偏差、風等干擾因素的存在,彈道將偏離基準彈道形成彈丸落點的偏差,稱該彈道為擾動彈道。

定義XT=Φ(x,y,z,vx,vy,vz)為基準彈道的函數表達式,函數以x為自變量,以vx,vy,vz,y,z為狀態變量,且函數在任意一點連續可微。令XIm(xIm,yIm,zIm)為擾動彈道的落點。若落點XIm與目標點XT距離較近,可在基準彈道任一點X(x,y,z)處采用泰勒展開的方法計算擾動彈道的落點坐標(僅給出二階泰勒展開),即:

(2)

式中:Φx,Φz分別為射程和橫偏的函數;Xp=(ΔvxΔvyΔvzΔyΔz)T;Δvx,Δvy,Δvz,Δy,Δz為射程x處的狀態變量的偏差量;V=(vxvyvz);Rx(X,V),Rz(X,V)分別為落點縱向坐標xIm、橫向坐標zIm泰勒展開的拉格朗日余項。

式(2)整理可得:

(3)

式中:ΔL,ΔH分別為縱向、橫向的落點偏差。

2.2 變增益修正比例導引

若目標靜止XT(xT,yT,zT),彈丸在空中任意位置為X(x,y,z),則可得彈丸在豎直平面和水平面內的視線轉率分別為

(4)

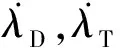
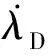
(5)

式中:θcx,n,σcx,n分別為當前時刻的彈道傾角程序角、彈道偏角程序角;θcx,n-1,σcx,n-1分別為上一時刻的彈道傾角程序角、彈道偏角程序角;Kθ,Kσ分別為豎直平面和水平面內的比例系數;Δt為兩時刻的時間間隔。

當前時刻彈道傾角和彈道偏角分別為

(6)

式中:θn,σn分別為當前時刻的彈道傾角、彈道偏角;vn為當前時刻彈丸的合速度;vxn,vyn,vzn為彈丸合速度在發射系坐標軸上的分量。

則有:

(7)

式中:Uθn,Uσn為導引信號。通過導引信號與彈丸的控制特性即可給出控制信號。

變增益比例導引中增益系數Kθ和Kσ為變量,其計算方法如下:

①搜索發射高低角和發射方位角,使彈丸精確命中目標點。

②使用如下公式計算Kθ和Kσ的值:

(8)

式中:θn-1,σn-1分別為上一時刻的彈道傾角、彈道偏角。

③得到一組Kθ和Kσ,在有控彈道仿真中使用插值的方法獲得相應的比例系數。

④導引系數解算同經典比例導引算法。

該方法的優點在于:在彈道較為彎曲處使用較大的比例系數提供較大的可用過載,使彈道末段的需用過載變小,從而減小脫靶量。然而,此處需要研究的問題是采用哪個變量對比例系數進行插值,可用于插值的變量有飛行時間、射程和動壓。

2.3 修正比例導引算法

攝動+比例導引復合導引算法是指將通過攝動方法預測的落點偏差作為補償量添加至變增益比例導引算法中,進行控制信號的解算,即

(9)

式中:kθ,kσ分別為縱向偏差和橫向偏差的補償系數,系數值的選取需通過仿真分析進行選取。

2.4 控制信號生成

依據文獻[16]中滾轉導彈的彈體傳遞函數的建立方法,建立旋轉穩定彈丸的彈體傳遞函數。

(10)

式中:Wθ,Wσ分別為豎直方向和水平方向的彈體傳遞函數,a22表征彈丸的赤道阻尼力矩特性,a24表征彈丸翻轉力矩特性,a25表征控制力矩特性,a′27表征彈體的馬格努斯力矩特性,a′28表征彈體的陀螺力矩特性,a34表征彈體的升力特性,a35表征操縱舵產生的控制力特性。

固定鴨舵式二維彈道修正引信采用單通道控制方案,即采用一對鴨舵實現對彈道的縱向和橫向修正,因而,需要綜合考慮彈丸縱向和橫向的傳遞系數來生成控制角。令A0=Wθ/Wσ,則有:

(11)

式中:γfk為控制角;Uθn,Uσn為使用預測落點偏差補償后的導引信號,φz為多項式擬合的相位滯后角。

3 仿真分析

3.1 算法精度分析

攝動+比例導引的復合導引算法:彈道上升段采用攝動落點預測法,下降段使用修正的比例導引。該算法以攝動落點偏差預測、比例導引算法和榴彈的控制相位滯后為基礎,因而算法誤差為三者綜合作用的結果。本文通過仿真的手段對算法精度進行分析。

首先通過搜索射角、射向使彈道精確命中目標,然后采用搜索所得的射角、射向進行修正彈的彈道仿真,仿真得到落點與目標點的偏差即為算法誤差。需要指出的是,仿真中不添加隨機擾動,且制導控制系統在理想狀態下工作,即制導控制系統無任何誤差。

彈道的仿真條件如表1所示,標準氣象條件下,彈丸以40.5°發射,稱2條彈道分別為基準彈道和有控彈道,如圖2所示。發射系中基準彈道和有控彈道的落點坐標分別為(2 5987.7 m,0,823.557 m)和(25 988.9 m,0,826.388 m),兩者的縱向偏差和橫向偏差分別為1.2 m和2.831 m。兩落點間的距離為3.075 m,即為算法誤差。

表1 基準彈道仿真參數設定

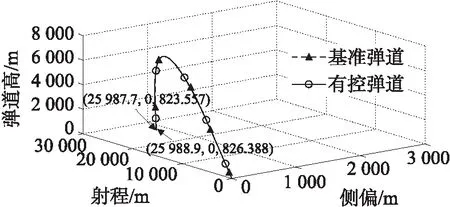
圖2 算法精度分析

為進一步驗證修正能力對算法精度的影響,進行了如下的仿真分析。通過調整影響彈丸無控落點散布的因素的偏差量,減小彈丸無控落點散布,而后進行有控打靶。若有控狀態下,落點散布CEP較小,則說明算法精度較高。仿真結果如圖3所示。

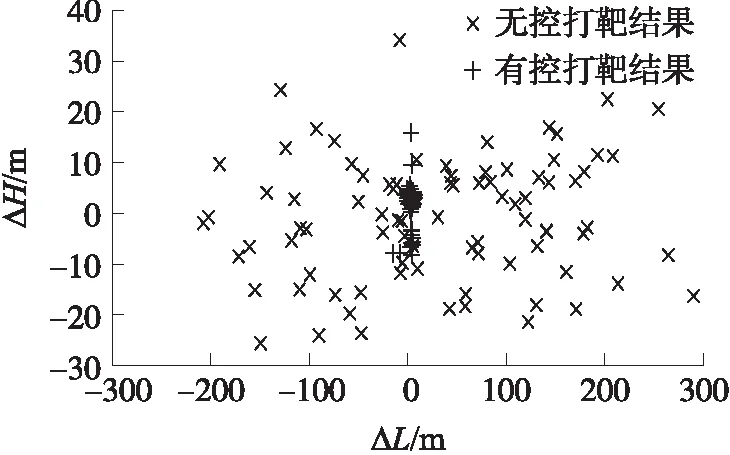
圖3 算法精度分析

經調整影響落點散布的偏差量,無控狀態下落點散布的縱向和橫向標準差分別為121.061 7 m和11.377 0 m,CEP為78.320 8 m;有控狀態下,縱向標準差和橫向標準差分別為3.717 1 m和4.039 2 m,CEP為4.603 2 m。該仿真結果充分說明,彈丸的修正能力制約了落點的修正控制精度,攝動+比例導引的復合導引算法的精度很高。

3.2 有控彈道仿真

目標點距26 km,彈丸初速為897 m/s,且仿真中不添加隨機干擾。經搜索,彈丸以40.5°射角發射時可精確命中目標,以此彈道為基準彈道。修正彈射角為39.5°,其彈道為有控彈道。仿真結果如圖4～圖7所示。

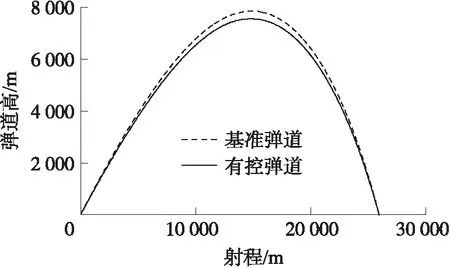
圖4 射程-彈道高曲線

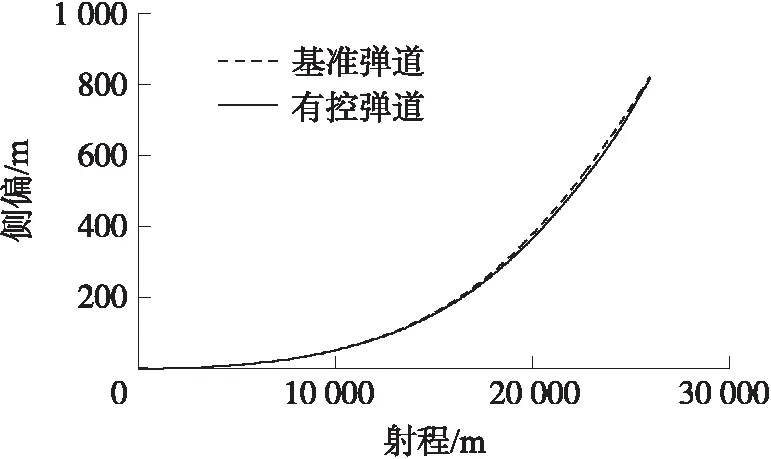
圖5 射程-橫偏曲線

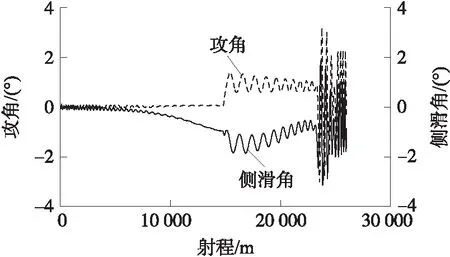
圖6 攻角和側滑角曲線

目標點在發射系中的坐標為(25 987.7 m,0,823.557 m),有控彈道落點坐標為(25 982.1 m,0,818.813 m),落點縱向偏差和橫向偏差分別為-5.6 m和-4.744 m。由圖5可知,有控彈道攻角從起控前的0°附近階躍至起控后的1°,側滑角的平均位置在數值上僅增加了0.2°左右,與理論分析一致。在23～25 km段,攻角、側滑角曲線變化頻率較高,但振幅不超過2°,該現象由控制信號的抖動引起。攻角、側滑角振幅在2°以內驗證了彈丸的穩定性。

3.3 蒙特卡洛打靶

圖7為采用攝動+比例導引算法的彈丸的打靶結果,打靶中僅考慮彈丸的隨機擾動。落點的縱向標準差為22.835 7 m,橫向標準差為23.579 2 m,CEP為27.507 0 m。圖中,修正能力曲線內的點在修正控制下均能精確命中目標,修正能力曲線外的點在不斷地向目標點逼近,且充分發揮了彈丸的修正能力。仿真結果表明,攝動+比例導引的復合導引算法可有效應用于修正彈的制導控制系統。

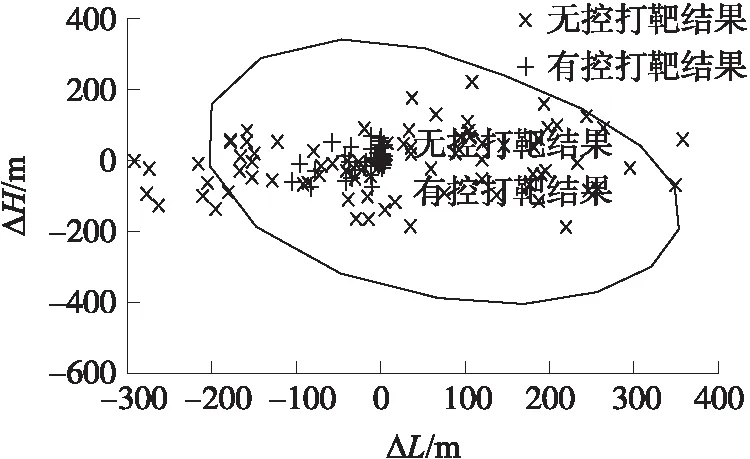
圖7 隨機擾動下的落點散布

4 結束語

采用固定鴨舵式二維彈道修正組件對傳統彈藥引信進行替代,是實現大口徑炮彈低成本彈道修正的重要途經。本文綜合攝動落點預測與修正比例導引算法:上升段運用攝動落點預測進行橫向修正,降弧段采用修正比例導引算法進行綜合修正。研究結果表明,該算法精度較高,在采用一標準射擊條件下,算法誤差僅為3.075 m,且彈丸的修正能力制約了落點的修正控制精度。采用本文所用復合導引算法可有效提高該修正彈的射擊精度,減小射擊落點散布。