基于變密度法的超聲輔助焊接小車車架優化及疲勞強度預測

鄧海龍 劉 行 鄭 麗 劉其晨 郭玉鵬

(①內蒙古工業大學機械工程學院，內蒙古 呼和浩特010051；②鄂爾多斯市特種設備檢驗所，內蒙古 鄂爾多斯 017000)

隨著自動焊接技術的發展，為了提高焊接質量，超聲輔助焊接小車備受關注。利用磁力進行焊接吸附是目前最常見的吸附方式，但其磁力大小對于小車車架結構的要求較為苛刻，其結構材料冗余問題嚴重。絕大部分小車的車架材質為鋼，在循環載荷的作用下，鋼的內部失效問題嚴重，因此，通過優化手段解決其材料冗余問題并進行疲勞強度預測，用最少的材料得到結構的最佳力學性能[1-2]，成為了超聲輔助焊接小車當務之急。

近年來，設備輕量化設計及其疲勞強度可靠性評估預測已經成為開發設計中必須要考慮的環節。朱金光等[3]采用有限元對某底盤車架的強度和剛度進行分析，根據有限元分析結果對結構進行優化。陳志等[4]基于實測載荷譜，研究了玉米收獲機底盤車架的疲勞強度，并進行了結構優化。朱茂桃等[5]提出了基于有限元的橋殼疲勞強度預測方法，并模擬橋殼試驗條件下的疲勞載荷，借助疲勞強度分析軟件估算出橋殼各部分的疲勞損傷情況。孫清超等[6]利用超高周疲勞壽命計算的裂紋萌生模型和Paris 方程擬合得出葉輪用FV520B-I鋼的超高周疲勞行為及其疲勞強度預測模型。蒲翔等[7]基于Paris公式對鋼管混凝土管節點進行了疲勞強度預測分析，并通過算例分析驗證了其模型的精度。焊接小車結構材料疲勞強度預測備受矚目，在循環載荷的作用下，其內部失效與夾雜物[8]等冶金缺陷密切相關。特別是當加載循環周次大于106時，在夾雜物周圍會出現粗糙區域[9]。Sakai[10]將這一粗糙區域命名為“細顆粒區”(fine granular area，FGA)。綜上所述，將優化算法和疲勞強度預測模型相結合，以實測載荷為基礎，能夠大幅度提高優化效率和預測精度[11]。疲勞強度預測已成為焊接小車車架結構設計的主流趨勢。此外，對于超聲焊接領域智能小車的結構優化問題依然值得探討，即車架材料長壽命區FGA的形成依然沒有較好的機理，疲勞強度評估預測模型依然沒有合適的解決方案。

本研究以減輕結構質量、保證焊接性能為目的，基于ABAQUS軟件，對車架進行了靜力學分析、拓撲優化并提出了新的超聲輔助焊接小車車架設計方案；通過修正Paris法則，建立了超聲輔助焊接小車車架材料的疲勞強度預測模型。

1 仿真分析

1.1 有限元模型建立

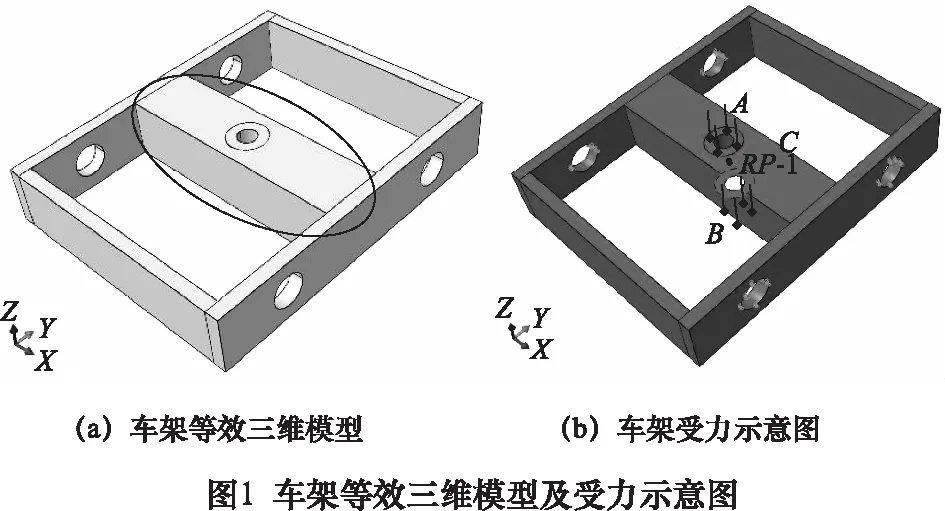
利用三維工程設計軟件UG NX10.0，對超聲輔助焊接小車車架進行三維建模，其三維模型如圖1a所示。車架部分全長500 mm，寬400 mm，高90 mm。本文對支撐永磁鐵安裝部分(如圖1a標記部分所示，后文稱為“中間長方體部分”)的結構進行拓撲優化分析，實現小車的輕量化設計。車架材料為12Cr-2Ni鋼，其力學參數，如表1所示。

表1 車架材料屬性

車架質量約為40 kg，機械臂和空化儀的總質量約為25 kg，控制單元的質量約為10 kg，永磁鐵的質量約為5 kg。本研究中選取焊接小車車架極限工況進行研究，即將焊接小車與地面的夾角為90°(實際上達不到)。車架上永磁鐵與焊接面距離為8 mm，經過計算并取安全系數S=1.5，求得最終所需磁力的大小約為2 000 N，且能夠吸附在焊接物表面。將該磁力加載在如圖1所示車架三維模型中間的等效受力圓環上，其面積約為5.024×10-3m2，可以求得此圓環面所受壓力約為0.41 MPa。

基于ABAQUS軟件，焊接小車車架等效三維模型如圖1a所示，考慮到后續拓撲優化的材料去除，為保證上下圓環不被去除，因此把壓力等效分解為壓力A、壓力B及螺紋耦合力C三部分，車架施加各部分平均載荷如表2所示。其中，螺紋耦合力需建立參考點RP-1，位置如圖1b所示，并建立該耦合點與空心圓柱面間的耦合關系。

1.2 靜力學分析

基于ABAQUS軟件，對車架三維模型進行網格劃分，網格單元數目為45 561，節點數目為71 587，網格的質量較好。車架所受載荷表及網格劃分結果如表2、圖2所示。

表2 車架載荷表

對車架模型進行靜力學分析，分析結果如圖3所示。由圖可知，最大應力發生在中間等效受力圓環處，值約為0.57 MPa，最大變形約為0.72 μm。此圓環處于應力集中區。12Cr-2Ni鋼的屈服極限是1 490 MPa，實際應力遠小于材料的屈服極限。此外，通過有限元分析結果可知，車架應力應變較小，材料冗余嚴重，有必要進行下一步拓撲優化。

2 車架結構優化

通過上述有限元分析結果可知，中間長方體部分的圓環上產生應力集中現象，且材料冗余。因此，基于ABAQUS對中間長方體部分進行拓撲優化[12]，以去除多余材料，實現車架的輕量化。本研究中所采用的優化方法為：以變密度法為基礎的拓撲優化方法和以優化準則法(OC)為基礎的迭代方法。

2.1 基于變密度法的拓撲優化方法

基于變密度法，結構拓撲有限元模型的每個單元均需賦密度值，相應的，設置拓撲結構彈性模量為[13]：

(1)

式中：xe為單元密度，服從0～1分布，即設計變量；p為懲罰指數，取值為3；E0為材料彈性模量；Emin為微小值，用以防止出現總剛矩陣奇異，取值為0.001。

選擇優化模型的設計區域(即中間長方體部分)，創建響應模式為應變響應，對設計區域的計算模式為“sum of values”，以結構柔度最小(外力功最小)為目標函數，體積分數比小于某值為約束條件，建立車架底盤的拓撲優化數學模型：

(2)

(3)

KU=F0≤xe≤1

式中：c為結構柔度；K、U與F分別為結構的整體剛度矩陣、節點位移矢量與載荷矢量；ue、k0和v0分別為單元節點位移矢量、單元剛度矩陣與單元體積；V0為設計區域體積；f為體積比；N為離散設計區域的單元數。

拓撲優化求解過程中，根據式(2)和式(3)得到目標函數和體積約束函數相對于設計變量的靈敏度為：

(4)

2.2 基于優化準則法(OC)的迭代方法

根據優化準則法并結合K-T條件，建立設計變量的迭代方程：

(5)

式中：k為優化迭代步數；h為阻尼系數，通常取0.5；m為變量移動距離，取正值0.2；Be為迭代系數；γ為拉格朗日乘子。

迭代過程中需滿足體積約束條件，利用半分法求解得到γ。拓撲優化迭代終止準則根據設計變量的絕對誤差決定，其數學表達式為：

(6)

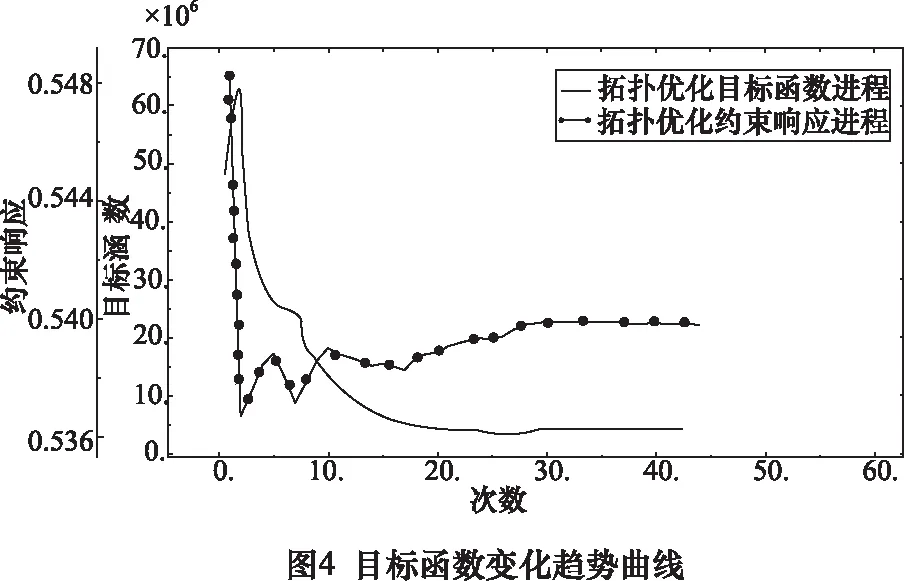
在迭代循環時，材料密度容易突變導致不收斂，故對初始密度比值設置為0.1[14]。在體積約束比取為0.54時，經過43次迭代步，優化結果最好：目標函數變化趨勢曲線如圖4所示：目標函數曲線大約在第20次迭代時收斂，收斂值約為3.14×106；體積約束曲線大約在第27次迭代時收斂，收斂值約為0.54。

施加與原車架相同載荷，最終拓撲優化結果如圖5所示，圖中可以看出，中間長方體部分優化成兩條相互交織的加強筋的形狀，小車此時的質量為25 kg，比原來減小了37.5%，并且滿足強度、剛度性能以及易加工的要求[15]，達到了優化設計的目的。

優化后的車架模型與原車架模型的結構性能以及質量對比，如表3所示。

表3 新車架模型與原車架模型結構性能對比

3 試驗與分析

3.1 試驗及載荷數據采集

基于100 kN高頻疲勞試驗機，對12Cr-2Ni鋼標準試樣進行疲勞試樣。其加載方式為軸向，試驗溫度為室溫，試驗頻率為133 Hz，應力比為0.3。

通過對斷裂表面特別是裂紋形核部位的初步掃描電鏡觀察，這種鋼呈現出連續下降的S-N特性。針對半對數坐標系下各部分試驗數據的非線性分布特點，采用Basquin模型建立了長壽命試驗數據對應的S-N曲線，如圖6所示，試驗壽命約為108周次時，試驗所得材料疲勞強度約為300 MPa。

3.2 疲勞強度預測

在長壽命區，試樣疲勞斷口主要為內部疲勞失效，如圖7a所示。當加載載荷次數超過106時，夾雜物周圍會出現“細顆粒區”(fine granular area，FGA)，如圖7b所示。

基于疲勞斷口，可以獲得不同應力水平下的夾雜尺寸和FGA尺寸，找出疲勞試樣在不同加載次數下的內部夾雜尺寸Rinc、FGA尺寸RFGA和魚眼尺寸R，如圖8所示。可以得出二者之間比例關系，并確立12Cr-2Ni鋼在焊接小車車架疲勞試樣內部夾雜尺寸與壽命之間的關系表達式：

(7)

(8)

于是，長壽命時期內部夾雜尺寸與疲勞壽命之間的關系為：

(9)

基于Matlab軟件，對疲勞強度預測模型進行擬合，選取的材料常數和夾雜物尺寸分別為：CA=14.3，mA=3.096，Rinc=13.45，預測構成車架材料的12Cr-2Ni結構鋼的強度預測模型擬合S-N曲線如圖9所示。

因此，當CA和mA的值以及夾雜物的大小已知時，利用式(9)可以建立不同斷裂機制對應的內部S-N曲線。根據內部夾雜尺寸，預測構成車架材料的12Cr-2Ni結構鋼的內部S-N曲線如圖9所示。由圖9可得，車架材料預測疲勞強度約為280 MPa，與原試驗數據相比，此預測疲勞強度誤差較小且可靠。

4 結語

以超聲輔助焊接小車車架為研究對象，首先對其在極限工況下進行了靜力學分析、拓撲優化設計，提出了新的超聲輔助焊接小車車架設計方案，最后進行車架疲勞強度預測。新車架模型與原車架模型相比質量減輕了37.5%，實現了超聲焊接小車的輕量化設計。構建了車架材料疲勞強度預測模型，且較為安全可靠。對探索超聲輔助焊接領域智能焊接小車的結構優化設計方法以及構建12Cr-2Ni鋼疲勞強度預測模型具有一定的借鑒意義。