基于支持向量機的實踐及應用

雷湘琦

摘要：本文使用的支持向量機以訓練誤差作為優化問題的約束條件，以置信范圍值最小化作為優化目標，即SVM是一種基于結構風險最小化準則的學習方法，其推廣能力優于其他的一些機器學習方法。現今運用的都是一些比較經典的算法，如傳統的決策樹算法等，同時這些算法也是學習數據挖掘算法的根基。文中主要列舉相關算法并應用相應的實例加以佐證，指出其中的不足和需要改進的地方。

關鍵詞：支持向量機;鳶尾花數據

引言

支持向量機（Support Vector Machine，SVM）SVM被提出于1964年，在二十世紀90年代后得到快速發展并衍生出一系列改進和擴展算法，在人像識別、文本分類等模式識別問題中有得到應用。它是一類按監督學習方式對數據進行二元分類的廣義線性分類器，其決策邊界是對學習樣本求解的最大邊距超平面。SVM使用鉸鏈損失函數計算經驗風險并在求解系統中加入了正則化項以優化結構風險，是一個具有稀疏性和穩健性的分類器。SVM可以通過核方法進行非線性分類，是常見的核學習方法之一。

1 基本原理

標準SVM是基于二元分類問題設計的算法，無法直接處理多分類問題。利用標準SVM的計算流程有序地構建多個決策邊界以實現樣本的多分類，通常的實現為“一對多”和“一對一”。一對多SVM對m個分類建立m個決策邊界，每個決策邊界判定一個分類對其余所有分類的歸屬;一對一SVM是一種投票法，其計算流程是對m個分類中的任意2個建立決策邊界，樣本的類別按其對所有決策邊界的判別結果中得分最高的類別選取。一對多SVM通過對標準SVM的優化問題進行修改可以實現一次迭代計算所有決策邊界

傳統的統計模式識別方式只有在樣本趨向無窮大的時候，其性能才有理論的保證。統計學習理論研究有限樣本情況下的機器學習問題。SVM的理論基礎就是統計學習理論。

根據統計學習理論，學習機器的實際風險由經驗風險值和置信范圍值兩部分組成。而基于經驗風險最小化準則的學習方法只強調了訓練樣本的經驗風險最小誤差，沒有最小化置信范圍值，因此其推廣能力較差。

1.1 尋找最佳超平面

SVM的主要目標是找到最佳超平面，以便在不同類的數據點之間進行正確分類。超平面維度等于輸入特征的數量減去1（例如，當使用三個特征時，超平面將是二維平面）。

為了分離兩類數據點，可以選擇許多可能的超平面。我們的目標是找到一個具有最大邊距的平面，即兩個類的數據點之間的最大距離。最大化邊距的目的是最大概率的對未知的數據點進行正確分類。

1.2超平面和支持向量

超平面是決策邊界，有助于對數據點進行分類。落在超平面兩側的數據點可歸因于不同的類。此外，超平面的尺寸取決于特征的數量。如果輸入要素的數量是2，則超平面只是一條線。如果輸入要素的數量是3，則超平面變為二維平面。當特征數量超過3時，就超出我們的想象了。

最接近超平面的數據點稱為支持向量。支持向量確定超平面的方向和位置，以便最大化分類器邊界（以及分類分數）。SVM算法應該使用的支持向量的數量可以根據應用任意選擇。

1.3 SVM內核

如果我們使用的數據不是線性可分的（因此導致線性SVM分類結果不佳），則可以應用稱為Kernel Trick的技術。此方法能夠將非線性可分離數據映射到更高維空間，使我們的數據可線性分離。使用這個新的維度空間SVM可以很容易地實現。

SVM中有許多不同類型的內核可用于創建這種更高維度的空間，例如線性，多項式，Sigmoid和徑向基函數（RBF）。在Scikit-Learn中，可以通過添加內核參數來指定內核函數svm.SVC，也可以通過gamma參數來指定內核對模型的影響。如果特征數量大于數據集中的樣本數量，則建議使用線性內核（否則RBF可能是更好的選擇）。

1.4 特征選擇

減少機器學習中的功能數量起著非常重要的作用，尤其是在處理大型數據集時。實際上，這可以：加速訓練，避免過度擬合，并最終通過降低數據噪音來獲得更好的分類結果。例如下圖中顯示了在Pima Indians糖尿病數據庫中使用SVM識別的主要特征。在綠色中顯示對應于負系數的所有特征，而藍色顯示為正系數。

1.5 支持向量機的算法

比較經典的如1）Vapnik提出的Chunking方法;其出發點是刪除矩陣中對應Lagrange乘數為零的行和列將不會影響最終結果，然而，在訓練集的支持向量數很大的時候，Chunking算法仍然無法將矩陣放入內存中;2）Qsuna提出的Qsuna算法;該算法存在效率問題，因為在每一步中，進行一次QP問題的最優化只能使一個樣本符合Kuhn-Tucker條件;3）Plat提出的序貫最小優化方法（sequential minimal optimization，簡稱SMO）;將一個大型的QP問題分解為一系列最小規模的QP子問題，即僅具有兩個Lagrange乘數的QP問題，從而使得原問題可以通過分析的方法加以解決，避免了在內循環中使用數值算法進行QP最優化。該算法在訓練線性SVM時，可以獲得非常好的性能。

2 數據選擇

Iris 鳶尾花數據集是一個經典數據集。數據集內包含 3 類共 150 條記錄，每類各 50 個數據，每條記錄都有 4 項特征：花萼長度、花萼寬度、花瓣長度、花瓣寬度，可以通過這4個特征預測鳶尾花卉屬于中的哪一品種。

3利用Support_Vector_Machines對Iris data進行分類

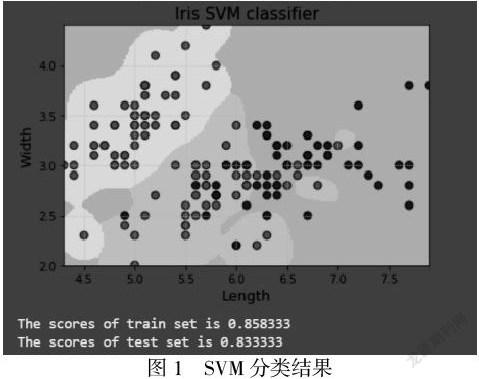
利用SVM對Iris data進行二分類后的到結果：

SVM是一種有堅實理論基礎的新穎的適用小樣本學習方法。它基本上不涉及概率測度及大數定律等，也簡化了通常的分類和回歸等問題。計算的復雜性取決于支持向量的數目，而不是樣本空間的維數，這在某種意義上避免了“維數災難”。因此可以利用已知的有效算法發現目標函數的全局最小值，有優秀的泛化能力。

參考文獻：

[1]程一芳.數據挖掘中的數據分類算法綜述[J].數字通信世界，2021（02）：136-137+140.

[2]韓成成，增思濤，林強，曹永春，滿正行.基于決策樹的流數據分類算法綜述[J].西北民族大學學報（自然科學版），2020，41（02）：20-30.

[3]李建新. 基于小波支持向量機的邊坡變形預測研究[D].江西理工大學，2020.

[4]姚奇峰，楊連賀.數據挖掘經典分類聚類算法的研究綜述[J].現代信息科技，2019，3（24）：86-88.

[5]李璐. 基于機器學習的滑坡地質災害預報模型研究[D].西安工程大學，2019.

[6]郭天頌. 基于粒子群優化支持向量機的滑坡易發性評價與滑坡位移預測[D].長安大學，2019.