ON REFINEMENT OF THE COEFFICIENT INEQUALITIES FOR A SUBCLASS OF QUASI-CONVEX MPPG RL L RB*

Qinghua XU(徐慶華) Yuanping LAI(賴元平)

School of Science,Zhejiang University of Science and Technology,Hangzhou 310023,China E-mail:xuqh@mail.ustc.edu.cn;lyp@163.com

For eachx∈X{0},we define

According to the Hahn-Banach theorem,T(x)is nonempty.

In[3],Fekete and Szeg¨o obtained the following classical result:

Let the functionf(z)be defined by(1.1).Iff∈S,then

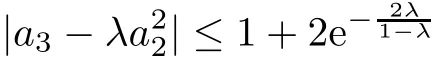
forλ∈[0,1].The above inequality is known as the Fekete and Szeg¨o inequality.After the appearance of this,there were many papers considering the corresponding problems for various subclasses of the class S,and many interesting results were obtained.For example,in[14],Keogh and Merkes obtained the following result for K:

Theorem A([14])Let the functionf(z)be defined by(1.1).Iff∈K,then

The above estimation is sharp for the function

Although the Fekete and Szeg¨o inequalities for various subclasses of the class S have been established,only a few results are known for the inequalities of homogeneous expansions for subclasses of biholomorphic mappings in several complex variables.Some best-possible results concerning the coefficient estimates for subclasses of holomorphic mappings in several variables were obtained in the works of Bracci et al.([1,2]),Graham et al.([4,6–9]),Hamada et al.([10–12]),Kohr([13]),Liu and Liu([19]),and Xu et al.([20,21]).

In[22],using a restrictive assumption,Xu and Liu established the coefficient inequality for a class of starlike mappings defined on the unit ball in a complex Banach space or on the unit polydisk in Cn,which is the first Fekete and Szeg¨o inequality in several complex variables.After this,the Fekete and Szeg¨o inequalities were established for well-known subclasses of biholomorphic mappings in several complex variables(see[24–27]).

In this article,we generalize Theorem A and obtain the Fekete and Szeg¨o inequality for a normalized convex functionfon U such thatf(z)?zhas a zero of orderk+1 atz=0,and then we extend this result to a subclass of quasi-convex mappings defined on the unit ball in a complex Banach space and the unit polydisk in Cn,respectively.The results presented here generalize the corresponding results of[23].

LetH(E)denote the set of all holomorphic mappings fromEintoX.It is well known that iff∈H(E),then

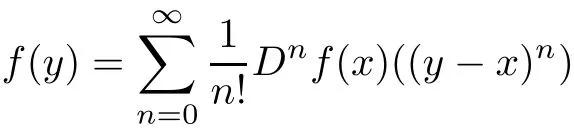
for allyin some neighborhood ofx∈E,whereDnf(x)is then-th-Fr′echet derivative offatE,forn≥1,

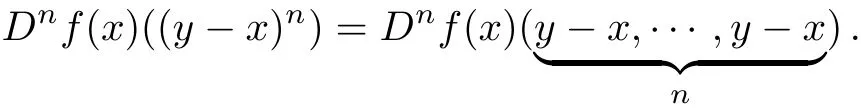
Furthermore,Dnf(x)is a bounded symmetricn-linear mapping fromintoX.

A holomorphic mappingf:E→Xis said to be biholomorphic if the inversef?1exists and is holomorphic on the open setf(E).A mappingf∈H(E)is said to be locally biholomorphic if the Fr′echet derivativeDf(x)has a bounded inverse for eachx∈E.Iff:E→Xis a holomorphic mapping,thenfis said to be normalized iff(0)=0 andDf(0)=I,whereIrepresents the linear identity operator fromXintoX.

Suppose that ??Cnis a bounded circular domain.The first Fr′echet derivative and them(m≥2)-th Fr′echet derivative of a mappingf∈H(?)at a pointz∈?are written byDf(z),Dmf(z)(am?1,.),respectively.The matrix representations are

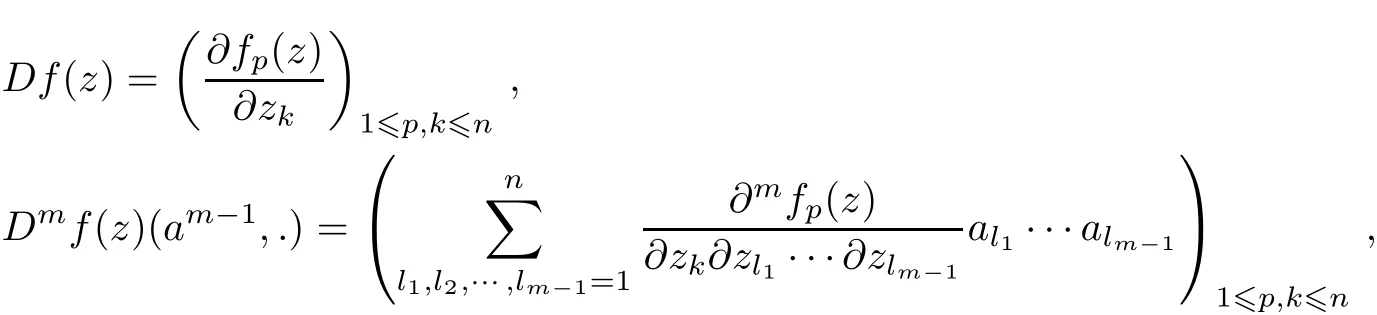
wheref(z)=(f1(z),f2(z),···,fn(z))′,a=(a1,a2,···,an)′∈Cn.

First,we recall the following definitions:

Definition 1.1([16])Letf:E→Xbe a normalized locally biholomorphic mapping.For allu∈?E,Tu∈T(u),α,β∈U,denote by

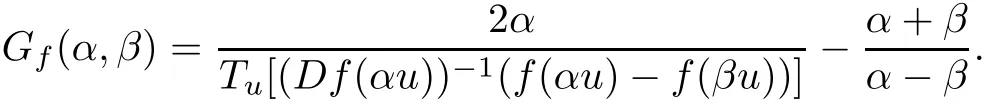
If

thenfis called a quasi-convex mapping of type A onE.

LetQA(E)denote the class of quasi-convex mappings of type A onE.

Definition 1.2([16])Letf:E→Xbe a normalized locally biholomorphic mapping.If

thenfis said to be a quasi-convex mapping of type B onE.

LetQB(E)denote the class of quasi-convex mappings of type B onE.

Definition 1.3([28])Letf:E→Xbe a normalized locally biholomorphic mapping.If

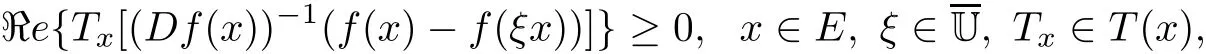
thenfis said to be a quasi-convex mapping of type C onE.

LetQC(E)denote the class of quasi-convex mappings of type C onE.

Remark 1.4([28])In[28],it was proved thatQA(E)=QC(E)?QB(E).WhenX=C,E=U,we deduce easily thatQA(U)=QB(U)=QC(U)=K.

Definition 1.5([17])Suppose that?is a domain(connected open set)inXwhich contains 0,andf:?→Xis a holomorphic mapping.We say thatx=0 is the zero of orderkoff(x)iff(0)=0,···,Dk?1f(0)=0,butDkf(0)≠0,wherek∈N.

2 Some Lemmas

In order to prove the desired results,we need to provide the following lemmas:

Lemma 2.1([5])Ifg(ξ)=b0+b1ξ+···+bnξn+···is holomorphic on U and|g(ξ)|<1 on U,then

3 Main Results

Now,we state and prove the main results of our present investigation.

From(3.15),together with(3.16),we deduce(3.3),as desired.

To see that the estimation of Theorem 3.3 is sharp,it suffices to consider the following example:as desired.

In order to prove the sharpness,it suffices to consider the following examples:

It is not difficult to check that the mappingsF,defined in(3.25)and(3.26),are in theQB(Un),and thatz=0 is the zero of orderk+1 ofF(z)?z.Takingz=(r,0,···,0)′(0

Remark 3.6Whenn=1,andk=1,Theorem 3.5 reduces to Theorem A.

Remark 3.7Theorems 3.3 and 3.5 generalize the corresponding results of[23].For whenk=1,Theorems 3.3 and 3.5 were obtained by Xu et al.[23].