ON VORTEX ALIGNMENT AND THE BOUNDEDNESS OF TH Lq-NORM OF VIRUICITY IN INCOMPRESSBLE VU FUD*
Siran LI(李思然)
Department of Mathematics, Rice University,MS 136 P.O. Box 1892,Houston, Texas,77251,USA
Current Address:Department of Mathematics,New York University-Sganghai,office 1146,1555 Century Avenue,Pudong,Shanghai 200122,China E-mail:siran.Li@rice.edu

where S is the 3×3 matrix

The alignment of the vorticity is closely related to the regularity of weak solutions to the Navier–Stokes equations.A celebrated result by Constantin–Fefferman[10]shows that,if the vorticity direction does not change too rapidly in the regions with high vorticity magnitude,then a weak solution is automatically strong.More precisely,denote
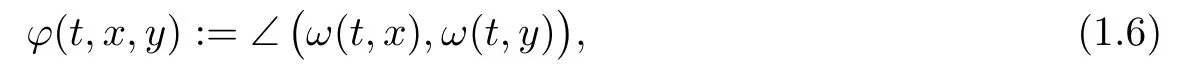
and if there are constantsΛandρ>0 such that

whenever|ω(t,x)|,|ω(t,y)|≥Λ,then a weak solutionuon[0,T]must be a classical solution on[0,T].Here,weak solutions are defined in the Leray–Hopf sense:u∈L∞(0,T;L2(R3))∩L2(0,T;H1(R3))with the energy inequality
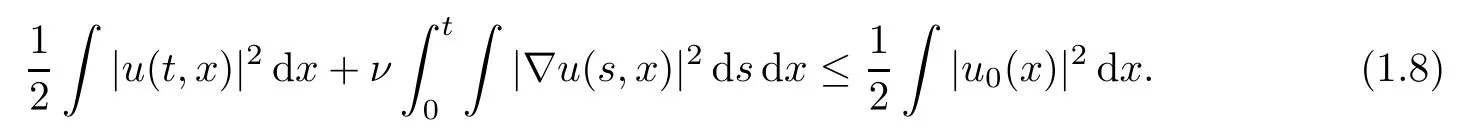
Throughout the paper,? without subscripts denotes integration over R3,and‖·‖Lq≡‖·‖Lq(R3).The above result of Constantin–Fefferman[10]is established by showing that
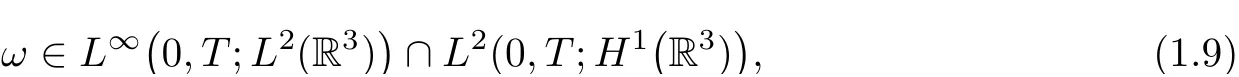
which,together with eq.(1.2),implies thatuis classical.Using more refined estimates,in[1],Beir?ao da Veiga–Berselli improved the Lipschitz condition(1.7)to a H¨older condition:
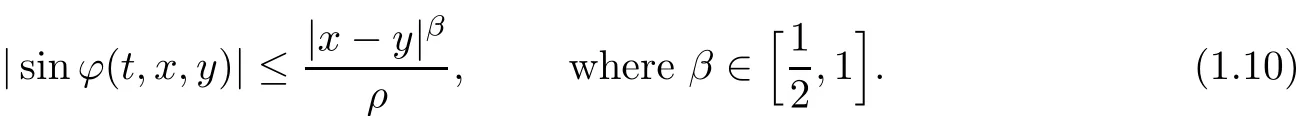
The H¨older exponentβ=1/2 is the best to date.There is extensive literature on the geometric regularity conditions`a la Constantin–Fefferman;see Beir?ao da Veiga–Berselli[1,2],Beir?ao da Veiga[4–6],Berselli[7],Chae[8],Chae–Kang–Li[9],Giga–Miura[14],Gruji′c[15],Vasseur[23],and Zhou[24],as well as the references cited therein.Similar conditions for the Euler equations have also been studied;cf.Constantin–Fefferman–Majda[11].
In this paper we establish a variant of the above results in[1,10].In contrast to eq.(1.9),which concerns the growth of theL2-norm of vorticityω,we study the growth of theLq-norm ofωunder assumptions of the form eq.(1.10),for which the H¨older exponent depends onqonly.
The main result of the paper is as follows:
Theorem 1.1Letu:R3×[0,T]→R3be a weak solution to eqs.(1.1)–(1.3).Assume that forq>5/3 there existΛandρ>0 such that

whenever|ω(t,x)|,|ω(t,y)|≥Λ;the angle?is as in eq.(1.6).In addition,suppose thatω∈Lq(R3×[0,T]).Then
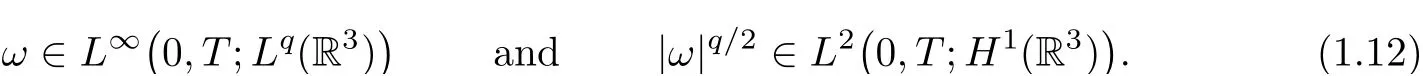
In particular,forq=2,β=1,Theorem 1.1 recovers the result by Constantin–Fefferman[10];and forq=2,β=1/2,the result by Beir?ao da Veiga–Berselli[1].Indeed,whenq=2,the assumptionω∈Lq(R3×[0,T])is automatically verified by the energy inequality(1.8).This result is consistent with the classical Prodi–Serrin regularity criterion(see[19,21]).
Theorem 1.1 provides a new characterisation for the control of vorticity under suitable alignment of the vortex structures in 3D incompressible fluids.Roughly speaking,it suggests a self-improvement property from the average-in-time bound for the(spatial)Lq-norm ofωto the uniform-in-time bound,provided that the vorticity does not change its direction too rapidly wherever its magnitude is large.

2 Preliminary Identities and Estimates
In this section we summarise several identities and inequalities that shall be used in the subsequent developments.
First of all,we recall the singular integral representation of the rate-of-strain tensor S in terms ofω,which is crucial to the arguments in Constantin–Fefferman[10].Denotinga:=a/|a|for three-vectorsa∈R3,it holds(eq.(4)in[10])that
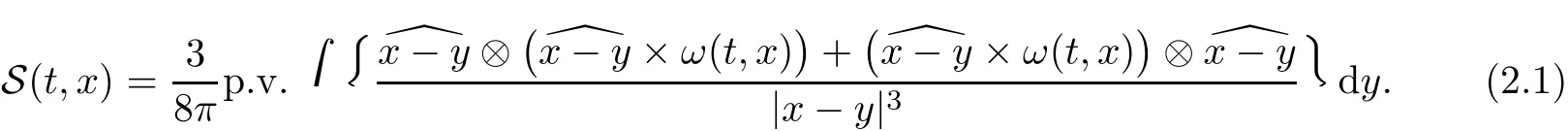
The symbol p.v.denotes the principal value.Then the vortex stretching term S:(ω?ω)can be expressed as
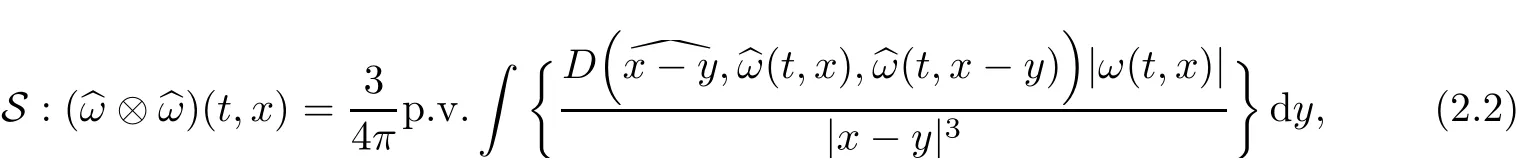
where
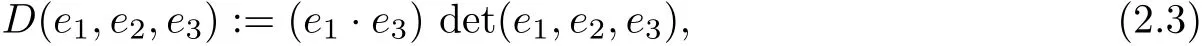
andeiare arbitrary three-vectors(column vectors)fori=1,2,3.As shown on pp.778–780 in[10],the bound for angle?can be translated to a bound for the geometrical termD:
Lemma 2.1Under the assumptions of Theorem 1.1,we have
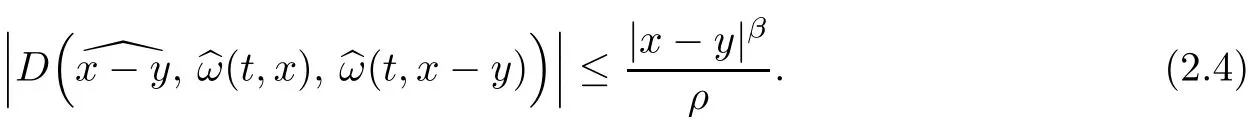
Next,the time-evolution of theLq-norm ofω(for anyq≥1)has been derived by Qian in[20],which is as follows.See the proof of Lemma 2 in[20].
Lemma 2.2Letube a weak solution to eqs.(1.1)–(1.3).Then,forq≥1,it holds that
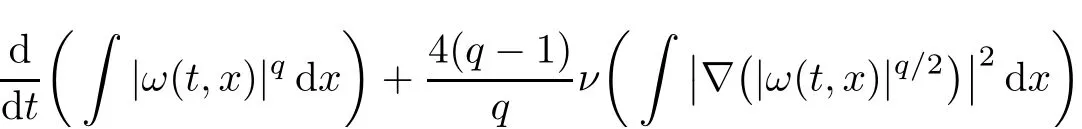
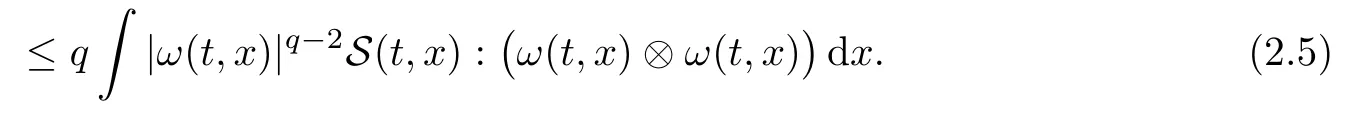
Finally,in Section 3,we shall make crucial use of the Hardy–Littlewood–Sobolev interpolation inequality(cf.p106,Lieb–Loss[17]),withn=3 andλ=2+δ.
Lemma 2.3Let 1 Equipped with Lemmas 2.1–2.3 above,we are ready to prove Theorem 1.1. As in Constantin–Fefferman[10],let us decompose the vorticity into“big”and“small”parts with respect to the(large)constantΛ>0 in Theorem 1.1.To this end,takingχ∈C∞([0,∞[),0≤χ≤1,χ≡1 on[0,1],andχ≡0 on[2,∞[,we define Putting together Cases 1 and 2 and using that 3?β=λ+2,we now complete the proof. AcknowledgementsThe author is indebted to Professor Zhongmin Qian for many insightful discussions and generous sharing of ideas,to Professor Gui-Qiang Chen for his lasting support,and to Professor Zoran Gruji′c for communicating with us about the paper[16].Part of this work was done during SL’s stay as a CRM–ISM postdoctoral fellow at the Centre de Recherches Math′ematiques,Universit′e de Montr′eal,and the Institut des Sciences Math′ematiques.The author would like to thank these institutions for their hospitality.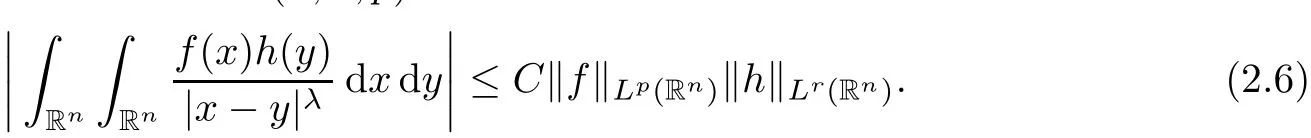
3 Proof of Theorem 1.1





 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- IT?O DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS?
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
