基于k-means聚類與粗糙集算法的指標篩選方法研究

張立軍，高春曉

(湖南大學 金融與統計學院，湖南 長沙 410079)

0 引言

在綜合評價問題中，運用恰當的方法進行指標篩選是不容忽視的重要環節，如果篩選出的指標體系不能系統全面地反映評價對象的特征，就會影響到最終的評價結果。粗糙集方法依靠其特有的數據挖掘和知識發現功能，能處理不精確、不確定、不完整的信息，具有較強的魯棒性和可操作性[1]。

目前，作為一種指標定量篩選的方法，利用指標間的某種相關性對評價指標進行篩選的方法得到了廣泛的應用，這類方法能夠剔除信息重疊的部分指標。通過相關性分析剔除信息重復性指標的方法主要有：

依據指標兩兩之間的相關程度刪除信息重復的指標，一是根據相關分析或偏相關分析剔除相關系數和偏相關系數比較高的部分指標。如張昆、遲國泰結合相關系數和粗糙集篩選出了生態評價指標體系[2]。陳險峰借助模糊隸屬度、差異性分析、相關性分析、信度與效度檢驗、穩定性與貼近度等技術指標探討了產業集群競爭力評價環節中的指標遴選問題[3]。二是利用互信息剔除反映信息重疊的指標[4]。互信息是利用信息熵測度指標間依賴程度的工具，屬于信息論研究方法。互信息的大小能夠反映指標相關性的強弱，互信息越大，關系越密切，該方法通常需要結合其他方法剔除相對不重要的指標。上述方法僅僅能夠度量兩個指標相互之間的相關性，并不能完全反映指標集內部的相關性，因此不能有效地降低指標集間的信息重疊。

(2)結合非參數統計、數據挖掘等理論分析指標間的相互關系，剔除冗余指標。如石寶峰、遲國泰等利用聚類方法分析每一類內相關程度高的指標，僅保留每一類中最重要的指標，從而間接減少指標間的重復信息[5]。又如王惠文等利用Gram-Schmid變換，構造正交的“主基底”，在盡量多的保留原始數據信息的情況下，排除所有的冗余變量及重疊信息[6]。再如侯娜等利用粗糙集約簡思想判斷灰色聚類結果的影響，篩選出的指標能顯著影響樣本分類的最終結果[7]。類似的，趙煥煥等利用灰色關聯分析的思想方法，構建了一種區間粗糙數多屬性決策方法[8]。這些研究利用客觀數據縮減了指標間的重復信息，但均忽略了對指標實際意義的考量。

針對現有方法的不足，本文提出了一種基于k-means聚類與粗糙集相對約簡原理的指標篩選方法，由樣本的空間分布密度得到改進的初始聚類中心點，進而實現基于k-means聚類算法的數據離散化過程，再由知識的相對約簡方法求解約簡的指標集，該方法既能夠對多余信息進行屬性約簡，又保證了指標的實際含義。

1 基于粗糙集理論的屬性約簡方法

1.1 連續屬性離散化

由于粗糙集的學習算法僅可以對離散數據的決策表進行處理，因此將連續屬性離散化就成為數據預處理的關鍵問題，其效果好壞直接影響數據分析結果。

目前，國內外學者已經針對連續屬性的離散化提出了一些高效通用的方法，根據是否利用類信息，離散化方法主要分為無監督方法和有監督方法兩種類型。k-means聚類離散化方法屬于一種無監督方法，該方法將距離作為相似性的測度，并把距離近的對象歸為一類或一簇，其能夠充分考慮每一維屬性的數據特點，使每一簇中的對象高度相似，同時使不同簇中的對象高度相異。但傳統的k-means聚類算法存在對初始聚類中心敏感度高的弊端，聚類結果會隨預先給定的聚類數目以及初始聚類中心的不同而產生波動，影響聚類的準確性和穩定性。為克服傳統k-means算法的上述缺陷，本文借鑒謝娟英等提出的聚類優化思想[9]，通過定義數據對象的空間分布密度并將高密度數據樣本作為初始聚類中心的方法，對基于k-means聚類的連續屬性的離散化過程做出了改進。

定義1已知樣本數據總體D={x1,x2,…,xn}，通過計算樣本相似性來衡量空間樣本密度，對象xi的空間分布密度記作density(xi)。

(1)

由式(1)可知，density(xi)越小，表明空間中樣本距離較近，樣本數據密度較大；density(xi)越大，表明空間中樣本距離越遠，樣本數據密度越小。

定義2對于任意數據對象x，將以x為中心，R為半徑所形成的圓形區域稱作數據對象x的鄰域，記為δ。

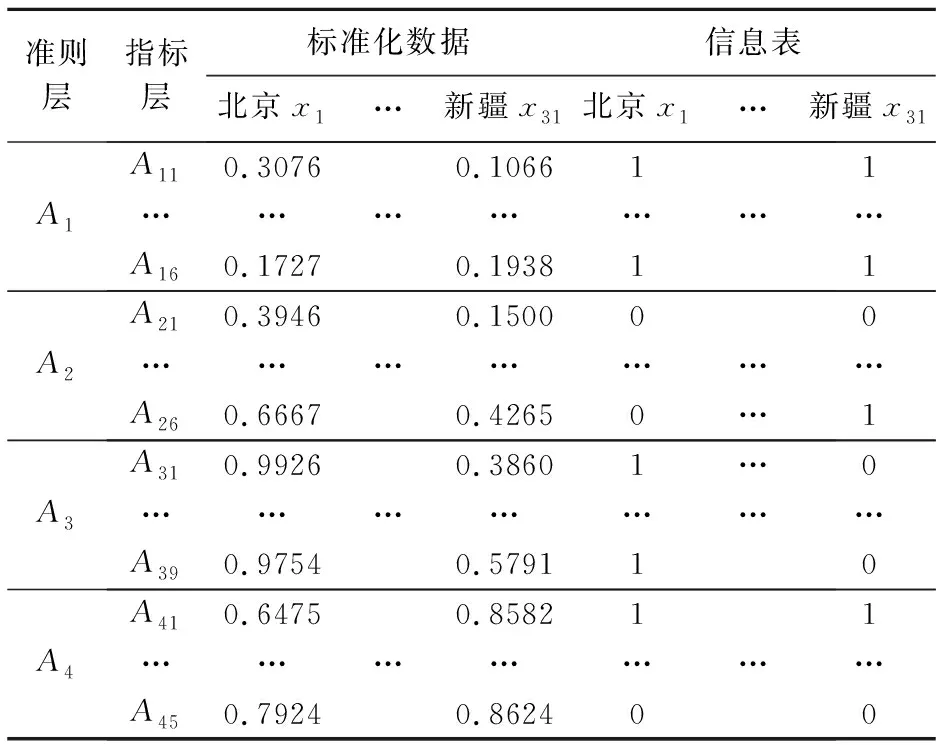
δ={x|0

(2)

定義3設樣本數據集X={xi|i=1,2,…,n}，則類簇平均質心距離的平均值記為E:

(3)

連續屬性離散化的具體算法步驟如下：

步驟1利用誤差平方和(SSE)指標確定初始聚類中心數目k并計算所有樣本對象的密度density(xi)，并定義一個初始化中心點集M={}；

步驟2選擇density(xi)最小的樣本對象xmin=min{xi|xi∈D,i=1,2,…,n}作為第一個初始中心點，添加到中心點集M中，即M=M∪{xmin}，并從樣本數據庫D中刪去該對象，即D=D-{xmin}，根據定義2計算xmin鄰域內的所有的樣本對象，并從樣本數據庫D中刪去；

步驟3重復執行步驟2，直到初始中心點集中有k個中心點作為初始聚類中心，即|M|=k；

步驟4根據歐氏距離來判斷相似度量，確定每個數據對象屬于哪個簇，計算并更新每個簇中對象的平均值，并將其確定為新的聚類中心；

步驟5計算類簇平均質心距離的平均值E；

步驟6循環步驟4、步驟5直到E收斂為止，得到聚類結果；

步驟7使用聚類結果中的類簇標簽代替類簇中數據的值，將連續屬性離散化。

1.2 粗糙集屬性約簡理論

近年來，粗糙集理論(Rough Set Theory, RST)[11]被廣泛用于機器學習、知識獲取、決策分析等領域。粗糙集方法應用于指標篩選，是根據粗糙集的屬性約簡原理，依賴于數據本身的性質從大量指標中剔除相關指標和冗余指標，提取核心指標，從而得到約簡指標體系。

定義4對每個屬性子集R?A，R在U上的不可分辨的二元關系IND(R)為：

IND(R)={(xi,xj)∈U×U,?r∈R,(r(xi)=r(xj))}

(4)

定理1設信息表S=(U,A,V,f)，R?A且r∈R。

如果IND(R)=IND(R-{r})，則稱r在R中是冗余的，否則r在R中是必要的。

假設Q∈R，若Q獨立，且IND(Q)=IND(P),則論域U在屬性集P上的約簡為Q，Q的所有約簡組成的集合記為Red(B)。

定義5若P?A,X?U,x∈U，集合X關于I的下近似為:

apr-P(X)=∪{x∈U:I(x)?X}

(5)

集合X關于I的上近似為：

(6)

X的P正域為:

posP(X)=apr-p(X)

(7)

若指標集A和指標集A-ai生成的等價類的數量一致，那么指標ai即為冗余指標，否則，指標ai即為不可或缺的指標。

設S?P，S為P的Q約簡，當且僅當S是P的Q獨立子族且posS(Q)=posP(Q)，P的Q約簡稱為相對約簡。

1.3 基于粗糙集的屬性約簡模型

在理論分析的基礎上，本文采用的基于粗糙集的屬性約簡思路如下：

(1)確定屬性集。根據初選指標確定屬性集，建立信息表。

(2)連續屬性的離散化。利用本文提出的基于改進k-means聚類的離散化方法對連續數據指標進行離散化，構建屬性約簡決策表，明確條件屬性和決策屬性。

(3)屬性約簡。求取粗糙集信息系統中評價對象的等價類，由知識的相對約簡原理刪除影響決策屬性的冗余指標。

(4)KW檢驗。對最終保留的指標作顯著性分析，以驗證指標篩選方法的效果。若KW檢驗中概率P值小于選定的顯著性水平，則拒絕原假設，表明篩選后的指標間存在顯著性差異，構建的指標體系是合理的。

圖1 指標篩選過程

2 實證分析

2.1 樣本選取及數據來源

本文選取2016年我國31個省、自治區和直轄市的綠色經濟指標數據，原始數據來源于2017年《中國統計年鑒》、《中國環境統計年鑒》、《中國城市建設統計年鑒》、《中國能源統計年鑒》、《中國教育統計年鑒》、《中國科技統計年鑒》和全國環境統計公報。

2.2 評價指標的初選

根據可獲得性、可測性與可操作性原則初選指標，保證初步篩選出的指標符合實際且可量化，能夠有足夠的客觀數據作支撐。從綠色經濟的內涵及基本特征、海內外權威機構及學者的研究成果[12,13]出發遴選出28個指標，并設置經濟發展、資源環境、社會民生、政策支持四個準則層，如表1所示。

表1 綠色經濟評價指標集及篩選結果

2.3 指標數據的標準化

指標數據的標準化，是通過數學變換將不同量綱或單位的數據無量綱化的方法。記第i個省份對應的第j個指標的標準化后值為mij(i=1，2，…，31；j=1,2,…)，第i個省份對應的第j個指標的原始數據為nij(i=1,2,…,31;j=1,2,…)。對于正向指標，指標數據越大，說明綠色經濟水平越高，正向指標的標準化公式為：

(8)

對于負向指標，指標數據越小，說明綠色經濟水平越高。負向指標的標準化公式為：

(9)

式中，mij∈[0,1]。

由式(8)和式(9)及表1中注明的指標類型，得到標準化處理后的值，列入表2。

表2 標準化數據及信息表

2.4 基于改進k-means聚類的數據離散化

將標準化后的數據按照1.1中的算法進行離散化處理。

利用R軟件計算出最優聚類中心數目，即k=2，按照步驟2、步驟3的方法計算得到初始聚類中心，進而得到離散化結果見表2。

2.5 基于決策表相對約簡原理的指標篩選

在將原始數據標準化和離散化的基礎上，以各準則層的指標作為條件屬性，以系統聚類結果作為決策屬性，將28個指標按照四個準則層分別形成四個決策表，運用R軟件進行編程，基于1.2中的相對約簡原理刪除準則層內對評價對象沒有顯著影響的指標。

現以經濟發展準則層為例，詳述該準則層指標的篩選過程，其他三個準則層的求解方法同理。經濟發展準則層的決策表如表3所示。

表3 經濟發展準則層的決策表

其中，U代表省份，x1～x31分別代表北京、天津等31個省，c1～c6分別代表國內生產總值、財政收入占GDP比重、失業率、第三產業比重、城鎮居民人均可支配收入6個影響決策指標的條件指標，D代表各省份的聚類結果。

令C={C1,C2,C3,C4,C5,C6}為條件屬性集，D=g0gggggg為決策屬性集，計算過程如下：

由C導出的等價類為:U/C={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x10,x11},{x9},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。

由D導出的等價類為：U/D={{x1,x3,x9,x10,x11,x15,x16,x17,x18,x19,x23},{x2,x4,x5,x6,x7,x8,x12,x13,x14,x20,x21,x22,x24,x25,x26,x27,x28,x29,x30,x31}}。

D的C正域：posC(D)={x1,x2,x9,x10,x11,x15,x16,x19,x31},U/(C-{c1})={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x9},{x10,x11},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。

D的C-{c1}正域：pos(C-{c1})(D)={x1,x2,x9,x10,x11,x15,x16,x19,x31}。

因此，pos(C-{c2})(C)≠posD(C)，c2是C中必要的，保留。同理可得：U/(C-{c2})={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x9},{x10,x11},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。

D的C-{c2}正域：pos(C-{c2})(D)={x1,x2,x9,x10,x11,x15,x16,x19}，因此，pos(C-{c2})(C)≠posD(C)，c2是C中必要的，保留。同理可得：pos(C-{c3})(C)=pos(C-{c6})(C)=posD(C)，pos(C-{c4})(C)≠pos(C-{c5})(C)≠posD(C)。

所以c1、c3、c6是C中D不必要的，約簡刪除，c2、c4、c5是C中D必要的，保留。經過相對約簡刪除后，經濟發展準則層剩余指標為財政收入占GDP比重、第三產業比重、城鎮居民人均可支配收入3個指標。

同理對資源環境、社會民生、政策支持三個準則層執行指標篩選過程，共刪除13個指標，保留突發環境事件次數、工業用水量、電力消費量等9個指標。

經過相對約簡刪除后，從28個海選指標中保留12個指標，最終篩選結果見表1。

2.6 指標篩選合理性分析

通過基于粗糙集相對約簡原理的指標篩選，在初選的28個指標中保留了12個指標，且在顯著性水平為0.05時，KW檢驗的檢驗概率值為0.007，說明構建的綠色經濟指標體系中各指標間具有顯著差異，從而驗證了指標篩選模型的合理性。

3 結論

本文針對k-means聚類結果對初始聚類中心具有敏感性的問題，定義了樣本空間分布密度，從而改進了k-means聚類離散化方法。在此基礎上，基于粗糙集知識的相對約簡原理，確定了指標體系的約簡，剔除包含重復信息的冗余指標。以綠色經濟評價指標體系的構建為實證對象，將初選的28個指標約簡為12個指標，驗證了基于k-means與粗糙集相對約簡原理的指標篩選模型的可行性。通過KW檢驗證明最終篩選的指標具有顯著性差異，說明了指標篩選模型的合理性。