考慮序列設置時間的混合流水車間多目標調度研究

黃 輝，李夢想，嚴 永

(西北工業(yè)大學 管理學院，陜西 西安 710072)

0 引言

隨著經濟社會的發(fā)展，技術水平和生活方式的革新與轉變，產品模式消費需求逐漸開啟了差異化個性化定制化的征程，相應的生產模式將更多的轉向多品種小批量的混合流水生產。目前，在生產周期，設備利用率，生產成本等各項指標下，混合流水生產企業(yè)正面臨著越來越復雜的生產調度問題，因此針對混合流水生產調度的研究也顯得愈發(fā)迫切與重要。

Naderi B等[1]研究了存在工序跳躍的混合流水車間調度(Hybrid Flow Shop Scheduling，HFSS)問題，以最小化最大完工周期為目標建立模型并求解。Dios M等[2]研究了存在工序跳過的混合流程車間調度問題，重點分析了存在工序跳過的HFSS問題的難度并設計了新的啟發(fā)式算法進行求解。Ebrahimi M等[3]研究了混合流水車間中依靠序列設置時間的調度問題，同時考慮交貨期的不確定性和隨機性，建立模型并求解。Nikjo B和Zarook Y[4]提出了一種新的考慮工件間設置時間的以最小化最大完工時間為目標的動態(tài)流水車間制造單元調度問題的數學模型并求解。徐建有等[5]和楊開兵等[6]考慮設置時間建立了多目標流水車間調度優(yōu)化模型并進行求解。喻明讓等[7]研究了考慮調整時間和機械故障的作業(yè)車間調度問題。周炳海和王騰[8]研究了考慮換模時間約束的混合流水車間調度問題。張煜等[9]研究了考慮設置時間和存在批處理機的HFSS問題。Visalakshi P和Sivanandam S N[10]研究了以負荷均衡為調度目標的動態(tài)車間調度問題。Pach C等[11]研究了以完工時間，能耗和資源轉換的數量為多目標的柔性制造車間的調度問題。賀利軍等[12]研究了以最大完工時間，最小化拖期時間，最小化庫存成本以及最小化拖期成本為多目標的流水車間調度問題。蔣增強和左樂[13]研究了以能源消耗，加工質量，最大完工時間，和加權成本為多目標的柔性作業(yè)車間調度問題。施進發(fā)等[14]研究了以最小機器總負荷，最小提前/拖期完工的懲罰值，最大設備利用率和成品合格率為多目標的柔性作業(yè)車間調度問題；顧澤平等[15]研究了以最小化最大流程時間、設備負荷均衡以及最大化設備利用率為優(yōu)化目標的柔性作業(yè)車間調度問題。

通過已有研究，可以發(fā)現(xiàn)在混合流水生產的研究中，針對帶有工序跳躍問題或序列設置時間約束的調度問題的研究相對較少，同時絕大部分文獻都是研究單目標的，其中以最小化最大完工時間為目標的最多，僅有少部分研究了多目標問題。而在實際的混合流水生產中，工序跳躍問題，設置時間問題以及調度的多目標化是非常常見的問題，且絕大多數生產系統(tǒng)都同時存在這三種問題，因此忽略這三個問題去研究生產系統(tǒng)調度，會由于與實際生產存在較大偏差而大大降低其研究價值和意義。本文在現(xiàn)有的研究基礎之上充分考慮這三個問題，建立相應的數學規(guī)劃模型并運用啟發(fā)式算法進行求解，更加貼合實際的生產調度系統(tǒng)，對豐富混合流水生產的研究內容和指導實際的生產調度都有很大的參考價值和意義。

1 混合流水車間調度模型構建

1.1 問題描述

混合流水線調度問題(hybrid flow-shop scheduling problem, HFSP)最早由Salvador于1973年提出。標準的HFSP可描述為：n個工件在m個階段的流水線上加工，各階段均有一臺或多臺機器且必須有不少于一個階段擁有兩臺及以上機器，同一階段上各機器的處理性能相同，各個工件必須且只需在每個階段的任意一臺機器上加工一次[16]。

在實際生產中，標準HFSP相對較少，大多是標準HFSP的變形，其中有些工件在加工時存在工序跳躍的現(xiàn)象比較常見。這時為了使所有任務在加工時都能符合混合流水生產的標準模式，不妨假設那些需要跳躍的工序也需要進行加工作業(yè)，即設置虛擬作業(yè)并將其加工作業(yè)時間設置為0，同時為了減小對其他作業(yè)順序的影響，可以設置虛擬的專用機器用于虛擬作業(yè)的加工，這樣企業(yè)的生產狀況就能符合混合流水生產的標準。相應的也就可以應用混合流水生產調度的方法和理論來針對企業(yè)現(xiàn)有的現(xiàn)狀和問題進行改進優(yōu)化研究。

1.2 模型假設

基于上述分析，本文可以構建企業(yè)的混合流水生產多目標調度優(yōu)化模型。為使構建的模型更加科學嚴謹，還需要對其他未被考慮的因素做出如下假設條件：

(1)不同調度方案的生產成本無差異；

(2)同一階段各加工設備屬相同并行機；

(3)每個加工任務在第一階段的發(fā)布時間均為0，且在其余階段均無時間窗限制；

(4)各加工任務經過其序列設置時間后立即開始加工；

(5)加工任務按照其優(yōu)先權進行排序，優(yōu)先權大的工件序號排在前面，在同等條件下可優(yōu)先進行加工；

(6)緩沖區(qū)容量為無窮大且操作允許等待，即加工任務的前一工序未完成，則后面的工序需要等待；

(7)每個任務的加工時間和序列設置時間事先給定，且在整個加工過程中保持不變；

(8)在加工任務存在工序跳躍的工序設定虛擬機器進行虛擬作業(yè)。

1.3 參數設置

(1)索引

i為加工任務索引，i∈{1,2,3,…,N}；

s為工序索引，s∈{1,2,3,…,S}；

k為工序s的機器索引，k∈{1,2,3,…,Ms}；

r為工序s下一加工工序snext的機器索引，若對應工件下一工序跳過則表示下下工序，以此類推，r∈{1,2,3,…,Ms}；

l為各工序各機器設備的位置索引，l∈{1,2,3,…,Ns,k}。

(2)參數

N為加工任務總數量；

S為總工序數量；

Ms為工序s的實際機器數量，不包括加工虛擬作業(yè)的虛擬機器；

Ns為工序s加工的任務數，若該工序不存在工序跳躍則Ns=N，反之Ns等于N減去跳躍的任務數；

Ns,k為工序s上機器k加工的總加工任務數；

ti,s,k為加工任務i在s工序的設備k上的加工時間；

ps,m,l-1,l為在s工序k機器上第l-1位置的加工任務到第l位置的加工任務的加工的序列設置時間，通常為換模時間。

(3)變量

Ui,s,k,l當加工任務i安排在工序s的機器k上的第l位置加工時Ui,s,k,l=1，反之，則Ui,s,k,l=0;

ci,s,k為加工任務i在s工序的k機器上的完工時間，若s=S則表示該加工任務的完工時間；

si,s,k為加工任務i在s工序的k機器上的開始加工時間；

si,snext,r為加工任務i在snext工序的r機器上的開始加工時間；

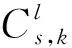
1.4 生產調度數學模型

本文充分考慮工序跳躍問題，設置時間問題和調度的多目標化三個重要指標，構建更加符合企業(yè)實際生產狀況的混合流水生產多目標調度優(yōu)化的數學模型如下:

minf1=Zp=min(max(ci,s,k))

(1)

(2)

公式(1)表示調度的目標函數1最小化最大完工時間，即最后一道工序的最大完工工時間最小；公式(2)表示調度目標2設備負荷均衡指標，即各工序內各機器設備的加工時間的標準差的均值；公式(3)表示機器約束，任意加工任務在任一工序只能在一臺機器設備上加工一次，若該任務在該工序存在工序跳躍，即使用虛擬機器進行虛擬作業(yè)，則可以忽略不記；公式(4)表示任務約束，即任意加工任務都必須在每個工序進行加工，不包括虛擬加工；公式(5)表示時間約束，只有前一工序的加工完成后才能開始下一工序的生產；公式(6)表示加工任務的完工時間等于開始時間加上加工任務的加工時間和序列設置時間；公式(7)表示設備只有上一加工任務加工結束后才能開始下一加工任務的加工；公式(8)表示工序內每臺機器設備的平均加工時間，不包括虛擬機器。

2 NSGA-II算法設計

參考同類研究可以發(fā)現(xiàn)多目標的GA更適合求解本文所研究的具體問題，常見有多目標遺傳算法(MOGA)，小生境Pareto遺傳算法(NPGA)，非支配解排序遺傳算法(NSGA和NSGA-II)等，其中在多目標的研究中，NSGA-II普遍具有更好的性能和效率。但是標準的NSGA-II在求解不同問題時也存在一定的不足之處，如在進行交叉變異操作時，其交叉變異參數固定不變，不利于最優(yōu)解搜索；精英保留策略選擇下一代時完全按照等級排序來選擇，未考慮進化后期會出現(xiàn)大量重復個體以至于種群多樣性大大減小，從而影響算法后期的搜索能力等。為了獲得更加準確的Pareto最優(yōu)解，本文針對NSGA-II的不足之處，設計了一種改進的NSGA-II算法來進行求解。

2.1 編碼設計

車間調度優(yōu)化問題常采用實數編碼，混合流水生產調度問題是車間調度問題的一種，因此本文也選用十進制編碼。由于混合流水生產需要把每個任務在每個階段的操作都表示出來的特殊性，在編碼時可以采用基于機器的矩陣編碼，這樣能更加清晰明了的把每個任務在每個階段的加工設備顯示出來，且能夠使解碼操作更加方便，不足之處是矩陣編碼不利于遺傳操作。為解決這個問題，本文選擇以矩陣思想設計編碼，即先構建虛擬矩陣，再運用函數將其轉化為行數組，數組與矩陣對應位置的特征相同，然后按照轉化的行數組特征來生成初始種群，并在解碼時可將其轉化為矩陣，最后在進行遺傳操作時仍在原數組進行。具體編碼方式為構建一個虛擬的N×S的矩陣(N為加工任務的數量，S為加工階段的數量)，如公式(9)所示，X為該調度問題的一個編碼(染色體)，表示該調度問題的一個可行解，即一個個體，矩陣中的xij表示任務i在j加工階段所使用的機器設備編號，其取值范圍取決于該工序的機器數量，若該工件在該工序的機器固定則只取一個固定的整數，若該工件需要跳過該工序，則取值為0。編碼時運用該矩陣轉化的行數組X′(如公式(10)所示)的特性生成數組形式的染色體，再在解碼時把行數組轉化為矩陣X″，如公式(11)所示。

(9)

X′=reshape(X,1,N×S)

=[x1,1,x2,1…xN,1,x1,2,

x2,2…xN,2…x1,S,x2,S…xN,S]

(10)

X″=reshape(X′,N,S)=X

(11)

2.2 NSGA-II算法的改進

2.2.1 種群初始化改進

種群初始化通常都是使用相應的函數根據設計好的染色體編碼隨機生成種群規(guī)模數量的染色體，這些染色體均為優(yōu)化問題的可行解，他們作為初始個體共同構成了初始種群P0。在生成初始種群時，為保障隨機概率性，各基因位的取值范圍設為實數區(qū)間，如有4臺機器設備，其取值范圍為「1,5)，在解碼時對實數進行向下取整，獲取相應的機器設備編號。此外，為了提高算法性能，往往還需要進行以下處理：一是讓初始種群盡可能均勻地分布在解的空間之內，以避免陷入局部最優(yōu)；二是采用一些簡單的方法對產生的初始解進行初步的篩選，剔除質量最差的一部分解。

針對本文所設計的染色體特征，可在初始化的染色體進行以下篩選以提高算法的搜索效率和質量：種群中每個個體的染色體需滿足每個工序中每個機器均被使用，否則該染色體需要重新生成，直到滿足該條件為止。

2.2.2 替換操作改進

基本NSGA-II算法的精英保留策略能夠保留各代種群中最好的個體，使算法性能和效率大大提升，但是隨著進化代數的增加，子代種群中逐漸會出現(xiàn)大量與父代種群相同且等級較高的個體，導致種群的多樣性也會迅速下降，進而出現(xiàn)早熟或者陷入局部最優(yōu)解的現(xiàn)象[17]。為彌補精英保留策略的這種不足之處，保證種群的多樣性以確保搜索方向朝著真正的Pareto解發(fā)展，本文針對基本的精英選擇策略進行了一定的改進，在執(zhí)行精英保留策略選擇下代種群時只選擇各等級種群中擁擠度不為0的個體，這樣就能保證相同個體最多只能選取兩個，這樣既保證了種群的多樣性，又在一定程度上提高了算法的搜索效率。

2.2.3 交叉參數改進

本文中交叉概率和變異概率相互補充，交叉概率越大，則變異概率越小，反之則變異概率越大。通常在算法求解的前期應優(yōu)先保證新個體的產生，因此交叉概率應相對較大，而后期算法相對收斂應擴大搜索范圍以避免陷入局部最優(yōu)，與此同時采用精英保留策略又能很好的消除變異率過大帶來的負面影響。據此本文設計一種自適應交叉概率參數，其交叉概率隨著遺傳代數的增加而自適應的降低，而變異概率則自適應的提高，交叉概率的具體取值如公式(12)所示：

(12)

式中t表示種群當前迭代數，T是指種群最大迭代次數，T1是指第一階段的最大迭代數，這里選擇為0.25T，T2是指第二階段的最大迭代數，這里選擇為0.75T，β為進化后期階段交叉率的調節(jié)系數，該系數的設置可以保證非支配集個體的交叉率在進化后期階段漸近于后期階段起始值的倍，其取值范圍為(0,1]，本文在進化后期為了避免交叉率過小，設置為β=0.8[18]。

3 算例驗證

3.1 算例數據

本文結合具體的混合流水車間生產的實際情況，根據車間實際數據來假定仿真的算理數據，主要包括生產資源數據和生產任務數據。在生產資源數據方面，混合流水車間共有4個工序，其各工序的設備數量如表1所示，在該生產車間中部分生產任務在工序2或者工序3存在工序跳躍。

表1 生產設備數量表

根據該車間歷史生產任務，假定了一定周期內的生產訂單作為仿真的任務，同時根據各個訂單的產品類型獲取這些生產任務在各工序的生產加工時間以及各任務之間的序列設置時間。本文共選取了20個生產任務進行仿真分析，其在各工序的加工時間數據如表2所示，各任務在各工序的序列設置時間表因篇幅原因不再展示。

3.2 基于改進NSGA-II算法的調度結果與分析

本文采用MATLAB軟件實現(xiàn)了基于改進NSGA-II算法的混合流水生產企業(yè)多目標優(yōu)化研究的算法設計及編碼求解，在實驗過程中，計算機的基本配置如下：(1)操作系統(tǒng)為Windows7 X64旗艦版；

(2)CPU為Intel core(TM)i5-2400，3.1GHz；

(3)內存RAM為4GB。

表2 各工序加工時間數據表(單位：小時)

基于上述企業(yè)的生產數據運行改進NSGA-II算法可求解出完成該生產任務的Pareto最優(yōu)調度方案，運行結果可得到負荷均衡指標Tlb進化收斂曲線圖，如圖1所示；最大完工時間目標Zp進化收斂曲線圖，如圖2所示；本次求解共求得10個Pareto最優(yōu)解集，如表3所示。

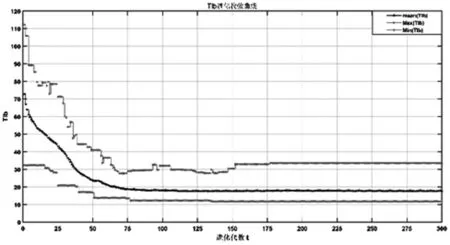
圖1 負荷均衡指標Tlb收斂曲線圖

圖2 最大完工時間Zp收斂曲線圖

圖1和圖2中最上方曲線分別表示各代種群中負荷均衡Tlb和最大完工時間Zp兩個目標的最大值收斂曲線，中間部分曲線分別表示各代種群中這兩個目標的均值收斂曲線，最下方曲線表示各代種群中兩個目標的最小值收斂曲線。由圖中可知：

(1)整體來看，在進化前期兩個優(yōu)化目標無論是均值還是最大值和最小值，都在迅速的減小并逐漸收斂，這表明了算法具有較好的性能，而在進化后期兩個目標的均值和最小值基本不變或稍微減少，最大值卻存在一定的波動，這表明算法在保留最優(yōu)解的同時還具有較強的持續(xù)搜索能力，在局部范圍內波動時兩者的波動存在一定的相關性，即兩個目標的最大值基本不同時減少，往往是在一個目標保持不變或者增大時迅速地減小，這表明在兩個目標在進化過程中不斷地相互均衡取舍，并最終達到相對的平衡；

(2)隨著進化代數t的增加，各代種群的負荷均衡目標Tlb和最大完工時間目標Zp的平均值先迅速減少然后逐漸趨于平穩(wěn)，并于100代之后分別收斂于18和375左右，在進化后期，各代種群中負荷均衡目標Tlb和最大完工時間目標Zp的均值始終更接近于最小值，這表明種群中的各可行解主要集中于最小值附近，而最大值的適當保留又表明了各代種群的多樣性，能夠提高進化過程的進化空間，有效的避免陷入局部最優(yōu)。

表3 Pareto最優(yōu)解集

本次優(yōu)化共生成10組帕累托最優(yōu)解，表3共展示有代表性的6組解，Pareto最優(yōu)解各行對應的是該工序上各加工任務所使用的機器編號，Zp和Tlb對應的是兩個目標值，單位為小時，從表中可以看出：

(1)從Pareto最優(yōu)解1～6可以看出，相鄰解的差異非常小，各任務中大部分任務在各工序的加工機器是完全相同的，僅有3～5個任務在部分工序上選擇的機器不同，即便是最優(yōu)解1和6這兩個目標距離最遠的解，也有一半的任務在各工序的加工機器完全相同，這表明算法在局部搜索時具有優(yōu)異的性能；

(2)在這6個解中，Pareto最優(yōu)解1的最大完工時間目標Zp最小，Pareto最優(yōu)解6的負荷均衡目標Tlb最小，在進行最優(yōu)調度方案選擇時，若決策者更加看重負荷均衡目標Tlb，則最佳決策方案更可能為Pareto最優(yōu)解6，反之若決策者更加注重最大完工時間目標Zp，則最佳決策方案更可能為Pareto最優(yōu)解1，若兩者之間相對平衡，則最優(yōu)解更可能為中間其他解；

根據所求解的Pareto最優(yōu)解集，可以繪制各個解的甘特圖，這里以Pareto最優(yōu)解6為例，其對應的甘特圖如圖3所示，虛線白框，黑框，實線白框和灰框依次對應第一道工序加工時間，第二道工序加工時間，第三道工序加工時間和第四道工序加工時間。從圖3中可以更加直觀的看到各加工任務在各工序加工時所使用的機器編號，起始加工時間以及各加工任務的完工時間，其中最后完工的加工任務為17號加工任務，其加工完工時間即為所有加工任務的最大完工時間。

圖3 Pareto最優(yōu)解6的甘特圖

4 結論

目前，在生產周期，設備利用率，生產成本等各項指標下，混合流水生產企業(yè)正面臨著越來越復雜的生產調度問題，針對混合流水生產調度的研究也顯得愈發(fā)迫切與重要，其中結合具體企業(yè)的研究更有理論意義和實用價值。因此本文結合混合流水車間多品種生產的特性，基于各個加工階段各加工設備在加工不同品種的產品時，需要一定的序列設置時間來完成設備設置、換模或調試等任務以及某些產品在加工時存在工序跳躍這兩種特征為主要約束條件，建立以能夠直接反映生產周期的最大完工時間和能夠有效反映生產效率的負荷均衡指標為雙目標的多目標調度優(yōu)化模型。并基于一定數據進行算例驗證分析，證明模型的有效性。該模型能夠有效的解決此類調度優(yōu)化問題，并為企業(yè)的實際調度提供一定的參考。