基于粒子群算法的水聲通信網絡能量優化方法

李朋偉，孟 荻，陳 倩

(海軍研究院，北京 100161)

0 引 言

水聲通信網絡(Underwater Acoustic Communication Network, UACN)在海洋及相關技術領域具有重要地位，可廣泛應用于海洋科學研究、氣象水文數據采集、重點海域監測、威脅目標警戒跟蹤等領域，發展前景廣闊[1]。但目前水聲通信網絡的發展水平與應用需求還有較大差距，其中，能量問題一直是影響水聲通信網絡發展應用的重要因素，而發展水下節點能量采集功能[2]和節點發射功率控制功能是解決水聲通信網絡能量問題的重要發展方向。

本文針對節點具備發射功率控制功能的網絡如何降低網絡節點總功耗，減緩網絡中節點死亡速率開展研究。對于固定節點，相比于節點電路功耗，節點上水聲換能器的功耗更大。因此，研究如何進行節點功率分配可有效降低節點發射功耗[3]。本文基于在滿足一定接收信噪比條件下的節點發射功率與傳輸距離的非線性關系，研究如何通過優化節點信息傳輸路徑，達到降低網絡節點總功耗的目的。

網絡分簇[4]是降低網絡節點總功耗、實現網絡能量優化的有效方法之一。文獻[5-6]針對最優分簇問題，提出LEACH、LEACH_L等分簇方法。文獻[7]結合水聲通信網絡節點功耗特點，基于節點擔任簇首次數、節點剩余能量及節點相對位置關系等，提出動態分簇方法，通過周期性輪換簇首，一定程度上降低了節點功耗，延緩了首個節點的死亡。文獻[8]通過引入水下節點發射功率與傳輸距離的關系，改進優化算法，進一步降低網絡節點總功耗。但在上述能量優化方法中，作者設定了簇首的最優數量，網絡中存活節點數量不斷減少，最優簇首數量始終不變。此外，按照上述所提優化方法，網絡采用周期性選簇，在每一個網絡周期開始前均需重新選簇，頻繁選簇帶來了大量的額外能量消耗。

分簇網絡中的簇首可視為節點采用兩跳路徑向目的節點發送信息時的中繼節點，因此，本文基于網絡中存活節點數量和節點剩余能量的變化情況，自適應確定中繼節點數量及中繼節點位置的最優方案，進而節點基于自身到不同中繼節點和目的節點的發射功耗，確定最優傳輸路徑。此外，針對優化過程帶來的額外能量損耗，本文改進了網絡模型，該模型采用事件觸發的方式啟動優化過程，減小了優化過程帶來的能量損耗。仿真結果表明，本文所提算法可有效降低網絡節點總功耗，延緩首個節點的死亡，減緩網絡中節點死亡速率，從而減緩網絡有效覆蓋面積隨著網絡運行而減小的速率。

1 節點能耗模型[8]

聲吶方程描述了發射聲源級(LS)、傳播損失(LT)、背景噪聲級(LN)、接收指向性(DI)及接收端信噪比(RSN)之間的關系，表達式為[9]

聲源級LS定義為

式中：Itrans表示距發射換能器聲學中心標準距離處的聲源強度。Iref為參考聲強，其值為0.67×10-18W·m-2。則節點發射電功率[9]為

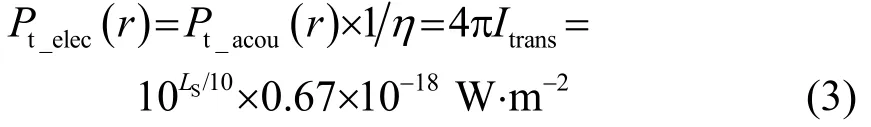
其中：Pt_acou為發射換能器聲功率，η為發射換能器的效率。

傳播損失[9]LT為

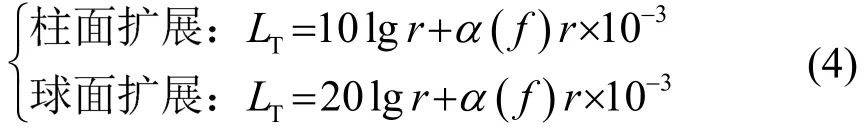
其中：r是通信距離，單位m；α(f)是聲信號吸收系數，單位dB·km-1，對于吸收系數，Thorp給出適用于低頻段的公式[10]，表達式為

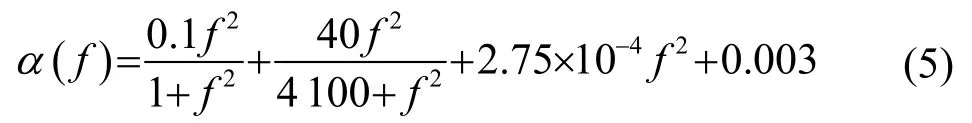
在滿足接收信噪比的條件下，依據式(1)～(5)，圖1給出了發射端最小發射電功率與通信距離的關系(柱面擴展，DI=0，LN=65 dB，LS=20 dB )。從圖1中可以看出，最小發射功率與通信距離呈非線性關系，距離越遠，最小發射功率增長越快。因此節點采用兩跳或多跳的方式向目的節點發送信息時，整個路徑上節點的功耗可能低于節點直接向目的節點發送信息的功耗。Stojanovic[11]的研究也表明，采用短距離多跳實現中遠距離水聲通信可獲得比單跳更低的節點發射功率。

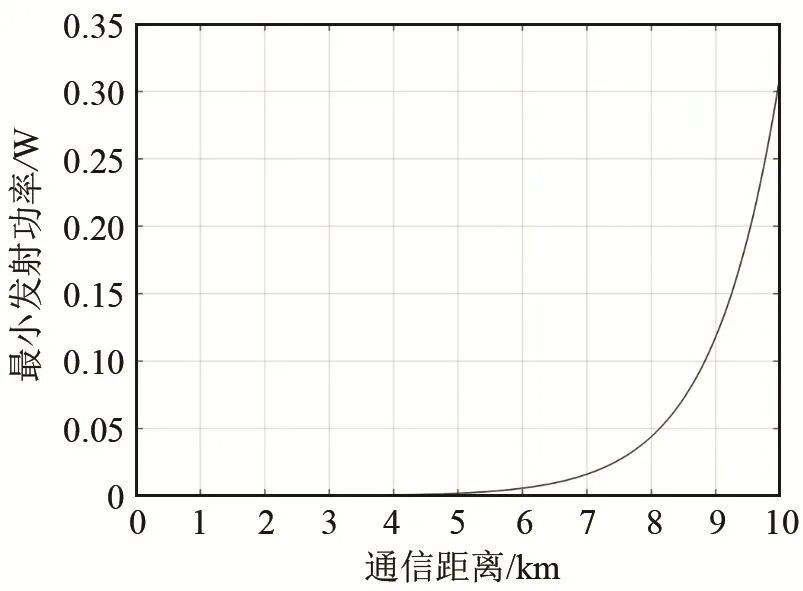
圖1 最小發射功率與通信距離關系Fig.1 Relationship between the required transmission power and the communication distance

在水聲換能器發射能耗基礎上，將節點的電路能耗加以考慮，發射端能量消耗可建模為

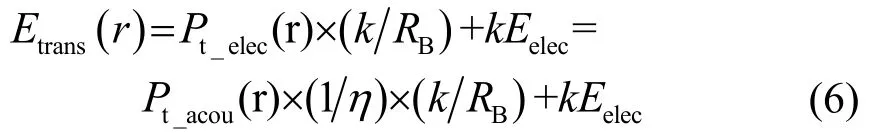
其中：RB表示信息傳輸速率，單位為bit·s-1，Eelec為發射換能器電路處理1 bit數據消耗的能量，k是發送信息量。

2 網絡模型

本文研究的水聲通信網絡由一個水面網關節點和若干水下節點組成，水下節點通過單跳或兩跳方式將信息傳輸到網關節點。水聲通信網絡進行過程如圖2所示。

運行過程分兩個階段：路徑優化階段和穩定運行階段。在路徑優化階段，網關節點運行第3節所提路徑優化算法，確定每個節點在網絡中的角色：中繼節點或普通節點，進而確定節點的最優信息傳輸路徑。普通節點指具備一定功能如水溫監測的節點；中繼節點除具備普通節點的功能外，還負責接收普通節點的信息并轉發到網關節點。路徑優化完成后網絡進入穩定運行階段。在該階段，普通節點通過分配的中繼節點向網關節點發送信息(兩跳)，中繼節點直接向網關節點發送信息(單跳)。網絡每經歷一次穩定運行階段，稱為一個周期。

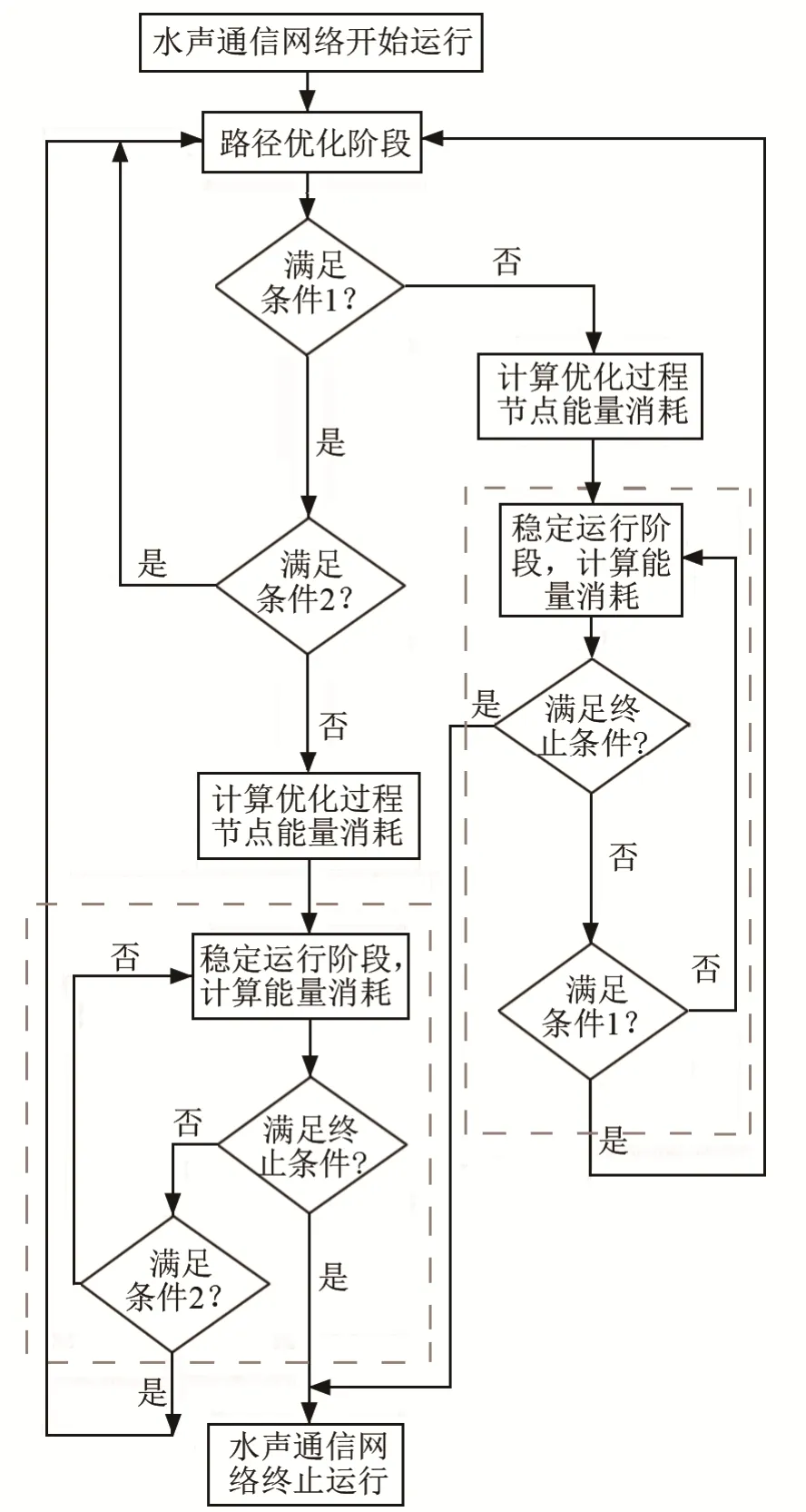
圖2 水聲通信網絡運行過程Fig.2 The operation process of underwater acoustic communication network

觸發網絡進入路徑優化階段的條件有兩個：(1)網絡中是否存在中繼節點的能量小于初始值的a%或是否出現死亡節點；(2) 是否存在中繼節點的能量大于初始值的a%或是否出現死亡節點(a用于判斷節點是否可作為中繼節點的候選節點，當節點當前能量小于初始能量的a%時，認為該節點剩余能量較少，不宜再承擔能耗較大的中繼節點角色)。針對所提水聲通信網絡模型，提出如下假設：

(1) 網關節點部署在區域中心且能量充足；

(2) 網關節點負責路徑優化方案生成并將方案發送到每一個節點；

(3) 節點的初始能量相同且具有發射功率控制功能；

(4) 穩定運行階段每個節點發送的信息量相同；

(5) 中繼節點對接收的信息直接轉發，不處理；

(6) 節點采用水聲換能器進行信號發射和接收。

3 路徑優化算法

3.1 目標函數

路徑優化的目的是降低網絡節點總功耗，減緩網絡中節點死亡速率，因此本文引入網絡中所有存活節點的發射總功率作為優化目標函數，表示為

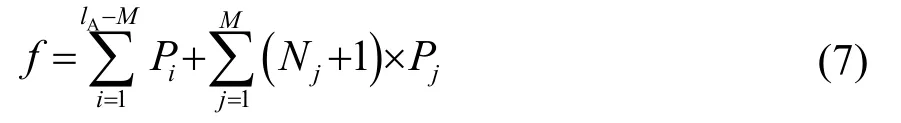
其中：lA為網絡中的存活節點總數，M為擔任中繼角色的節點數量。Pi為第i個普通節點的最小發射功率，Pj為第j個中繼節點的最小發射功率，Nj為以該節點為中繼節點的普通節點數量。網絡中擔任中繼角色的節點數量不同和不同節點擔任的角色方案不同，即每一個節點的信息傳輸路徑不同時，對應的目標函數值不同，目標函數值越小，表明網絡中存活節點的發射總功率越小。通過優化網絡中所有存活節點擔任角色的方案和擔任中繼角色的節點數量，可使所有存活節點的發射總功率最小。

3.2 優化算法

在路徑優化階段，網絡中不同節點擔任何種角色有多種組合方案，以3.1節中的目標函數為優化目標函數，從眾多方案中選擇出最優方案的過程可建模為尋優過程。對于該過程，粒子群算法以一定數量的方案為基礎，通過最優搜索，尋優獲得目標函數值最小時對應的優化路徑方案，該方案即是最優方案。相較于窮舉算法，粒子群算法的優點是優化效率高，獲得最優結果的時間更短。

以PSj表示第j個節點的角色，則所有節點的角色按照節點序號排列所形成的組合(lA為網絡中存活節點總數)可視為粒子群中的一個粒子，粒子群中的第i個粒子為,i=1…N(N為粒子群規模)。以3.1節中目標函數為粒子的適應度函數，利用粒子群算法獲得的最優粒子對應的節點角色方案即是最優節點角色方案。在最優角色方案的基礎上，普通節點基于自身到不同中繼節點和網關節點的發射功耗，確定是采用某一個中繼節點轉發信息，還是采用單跳方式向網關發送信息，由此即可獲得每一個節點的最優信息傳輸路徑。

本文在文獻[8]中基于改進的粒子算法的基礎上，綜合考慮網絡運行不同階段存活節點的數量，改進粒子群的初始化方式和變異算子，將自適應交叉概率和變異概率引入該算法中，形成新的優化算法，獲得較好的優化結果。算法流程如圖3所示。

圖3 能量優化算法的流程圖Fig.3 Flowchart of the energy optimization algorithm

(1) 粒子編碼

(2) 粒子群初始化

隨著水聲通信網絡運行，網絡中存活節點數量lA在不斷減少，因此應在路徑優化階段根據存活節點數量，在粒子群中自適應產生中繼節點數量的所有可能方案，即產生的粒子中中繼節點的可能數量為1～lA。本文采用輪換方式，依次產生中繼節點數量為1,2…lA的粒子，假設粒子群規模為N，則中繼節點數量分別為1,2,3…lA的粒子數量依次為

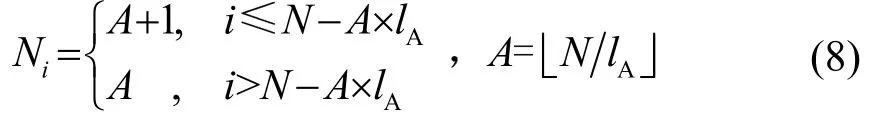
對于中繼節點數量為T的粒子，隨機選擇T個節點，將節點在粒子上對應的位置標記為1，死亡節點標記為?1，普通節點標記為0，不能作為候選中繼節點標記為2。完成粒子生成后，依次計算每個粒子的適應度值，并初始化歷史最優粒子(記為)和全局最優粒子(記為)。

(3) 自適應交叉概率和變異概率

采用正比選擇策略[12]。設粒子與歷史最優粒子交叉的初始交叉概率為PH0，按照式(9)獲得自適應交叉概率：

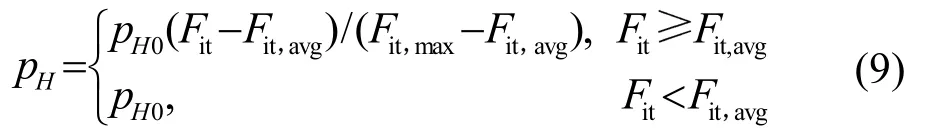
式中：Fit為粒子和其歷史最優粒子兩者中較大的適應度值，Fit，avg為每代種群與待交叉的歷史最優粒子組成的新群組的平均適應度值，Fit，max為新群組中最大的適應度值。

設粒子與全局最優粒子交叉的初始交叉概率為PA0，按照式(10)計算自適應交叉概率：

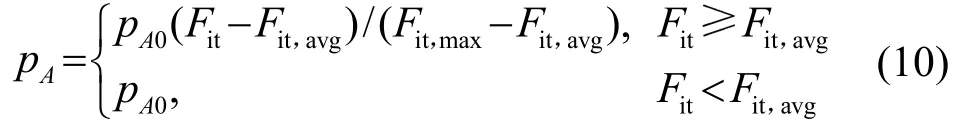
式中：Fit為粒子和全局最優粒子兩者中較大的適應度值，Fit，avg為每代種群與全局最優粒子組成的新群組的平均適應度值，Fit，max為新群組中最大的適應度值。

初始變異概率為Pm0，按照式(11)計算獲得：

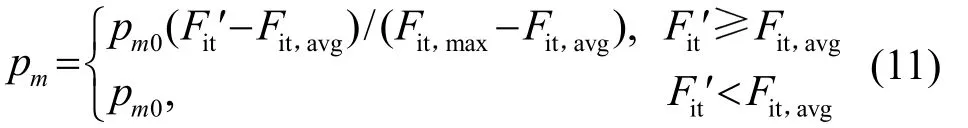
式中：Fit'為待變異個體的適應度值。

(4) 交叉算子

交叉算子與文獻[8]所提的交叉算子一致，當粒子與歷史最優粒子交叉時，需完整交叉含有兩個中繼節點的粒子片段，當粒子與全局最優粒子交叉時，需完整交叉一個中繼節點。

(5) 更新歷史最優粒子和全局最優粒子

用歷史最優粒子和全局最優粒子與粒子群中的粒子交叉獲得新粒子后，對粒子的歷史最優粒子和全局最優粒子進行更新，將產生的較優粒子保存。

(6) 變異算子

對每一個粒子，在該粒子上隨機選擇一個節點，當該節點標記為1時，將其變異為0；當該節點為0時，將其變異為1；當該節點為?1或2時，不變異。變異完成后，計算新粒子的適應度值，如果新粒子的適應度值優于變異前，則用新的粒子替換變異前的粒子，并更新該粒子的歷史最優粒子，否則不更新變異前的粒子。粒子群變異完成后更新歷史最優粒子和全局最優粒子。

4 仿真分析

采用Matlab2015a進行仿真。文獻[8]將所提算法與文獻[7]所提改進粒子群算法以及LEACH算法進行對比，仿真結果表明，文獻[8]所提算法可獲得更優的分簇結果，進一步降低了網絡節點總功耗，減緩節點死亡速率。本文將所提能量優化算法與文獻[8]所提算法進行對比。兩種方法的主要參數設置如表1所示。

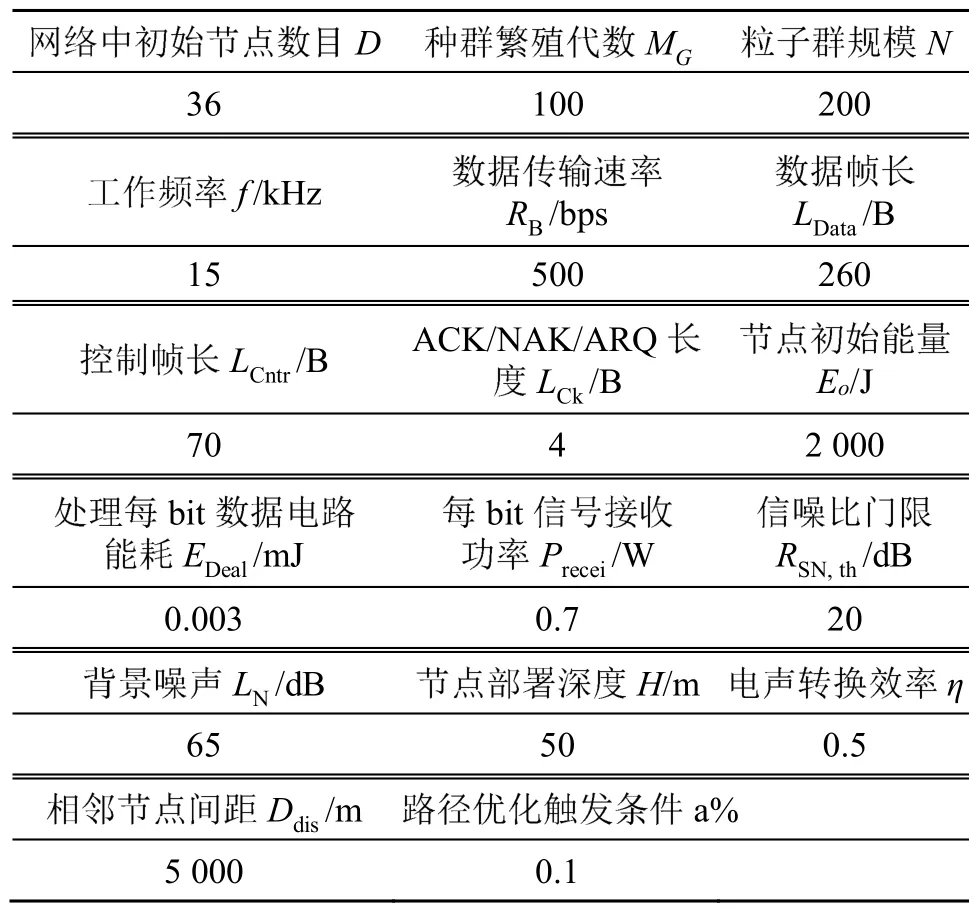
表1 本文及文獻[8]中能量優化算法主要參數設置Table 1 The main parameter setting for the energy optimization algorithms in this paper and in the reference[8]

本文算法其他仿真參數為PH0=0.9，PA0=0.9，Pm0=0.8。文獻[8]所提方法的其他仿真參數按照其給出的值，為a=0.5，b=0.25，c=0.25，c1=c2=0.1，w=0.729 8(a，b，c為文獻[8]所提的目標函數中不同因素所占比重，c1，c2，ω分別為粒子與歷史最優粒子的交叉概率、粒子與全局最優粒子的交叉概率和變異概率)。仿真中，節點接收信息的能量消耗模型為：Erecei=Pr_elec×(k/RB)+kEelec。

圖4和圖5給出了在網絡初始化時利用兩種方法獲得的最優傳輸路徑方案。

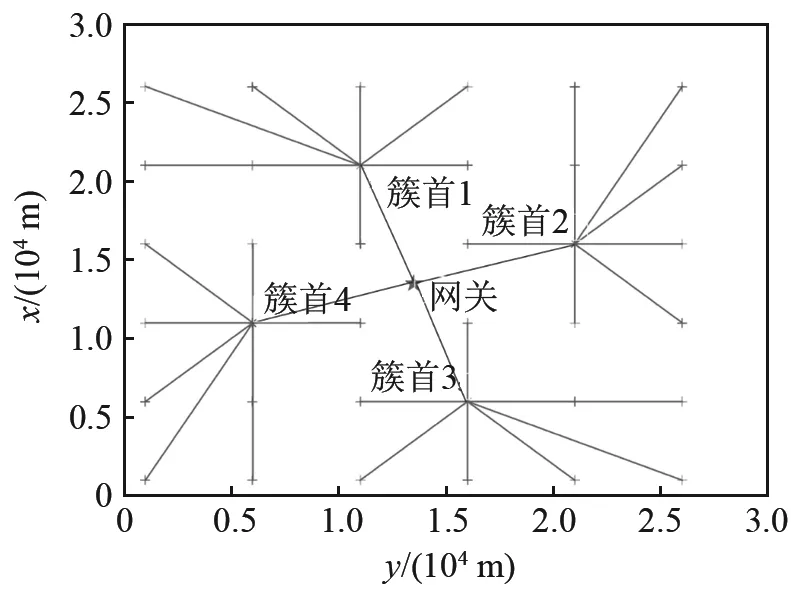
圖4 文獻[8]算法的最優傳輸路徑Fig.4 The optimized transmission paths of the algorithm in the reference[8]

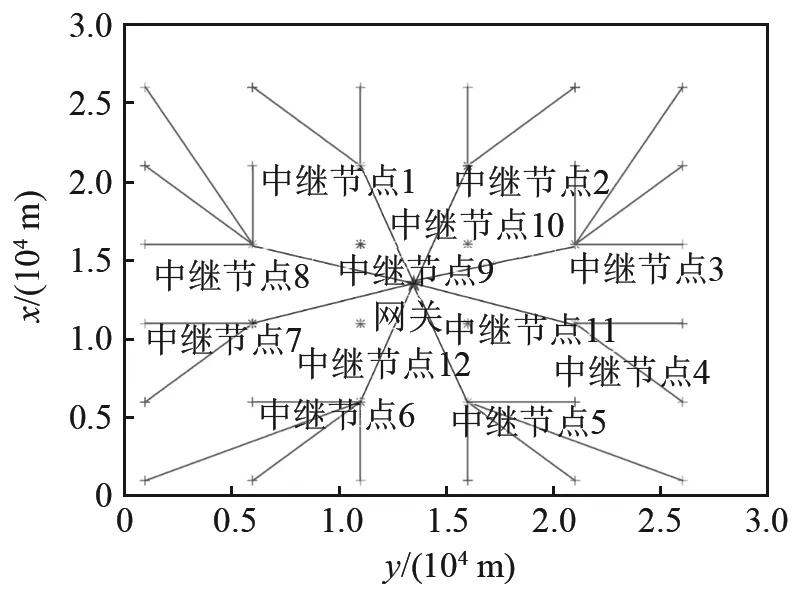
圖5 本文算法的最優傳輸路徑Fig.5 The optimized transmission paths of the proposed algorithm in this paper

圖4為文獻[8]算法獲得的最優路徑方案。在該方案中，32個普通節點被分配在4個簇中，普通節點利用簇首中繼向網關節點發送信息。圖5為本文算法的最優路徑方案。在該方案中，有 12個節點擔任中繼節點，普通節點利用 1～8 號中繼節點向網關節點發送信息，9～12號中繼節點僅負責將自身信息發送到網關節點。在最優路徑方案中，采用原算法的網絡節點總功耗為0.297 9 W，而采用本文算法的網絡節點總功耗為0.173 8 W，低于前者。

圖6比較了采用兩種算法的網絡中存活節點數量隨網絡運行的變化情況。

圖7比較了采用兩種算法的網絡中，網絡運行時，網絡剩余總能量的變化情況。由圖6可知，采用文獻[8]算法的網絡在第333個周期時出現首個死亡節點；而采用本文算法的網絡在第358個周期時出現首個死亡節點，比原算法延長 25個周期。第377個周期時，采用原算法的網絡存活節點數為0，網絡完全死亡，而采用本文算法的網絡存活節點數為28，表明網絡仍有較大覆蓋面積。第718個周期時，采用本文算法的網絡存活節點數降至4。綜上，仿真結果表明采用本文算法可延緩首個節點死亡時間，節點死亡速率更低。

從圖7中可以看出，采用本算法的網絡的能量始終高于原算法，說明采用本文算法的網絡的總功耗始終低于采用原算法的網絡。且從圖7中還可看出，在采用原算法的網絡已完全死亡時，采用本文算法的網絡的剩余總能量仍有1.376× 104J。

此外，粒子群規模N和種群繁殖代數MG影響粒子群算法的收斂速度、搜索結果與最優結果的逼近程度。N和MG取值較大時，雖然能獲得較優的搜索結果和較好的算法穩定性，但是搜索時間長，搜索效率低；N和MG取值較小時，會導致算法搜索結果不收斂。因此，粒子群規模和種群繁殖代數存在最優取值，而該值與節點數有關。取值原則一般為節點數越多，則粒子群規模和種群繁殖代數的最優取值越大。

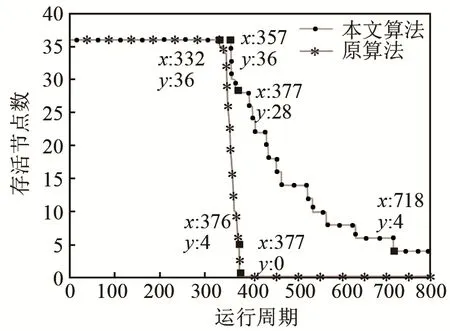
圖6 兩種算法存活節點數量的對比Fig.6 Comparison of the number of alive sensor nodes for the two algorithms

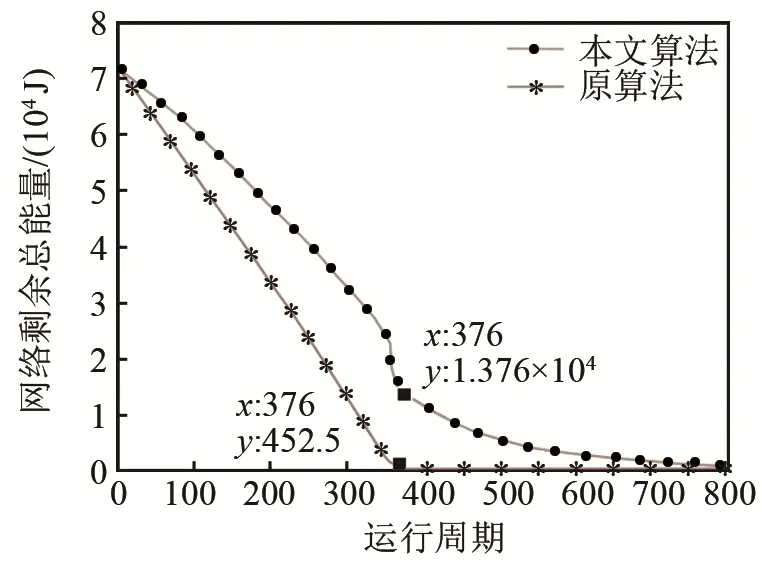
圖7 兩種算法網絡剩余能量的變化情況Fig.7 Comparison of the residual energy in the network for the two algorithms

因此在本文所述網絡中，隨著網絡運行，存活節點數在不斷變化，粒子群規模和種群繁殖代數的最優取值應是自適應變化的，自適應變化關系需作進一步詳細研究。為分析方便，本文僅考慮了隨著網絡運行，粒子群算法規模和種群繁殖代數取值不變的情況，采用蒙特卡洛仿真方法，表2、3給出了網絡中節點數為36個時，粒子群規模和種群繁殖代數取不同值時，算法搜索結果對應的網絡總功耗的均值和方差變化情況。

從表2、3中可知，在N=200時，當種群繁殖代數MG大于80，搜索結果均值保持不變，方差為0；在MG=100時，當粒子群規模N大于20，搜索結果均值保持不變，方差為0。因此當N=200，MG=80，或N=20，MG=100，算法均可獲得最優值，且搜索效率較高，當N和MG選取更大值時，算法也可獲得最優值，但搜索效率會下降。若需對搜索效率有進一步要求，可對N、MG的不同取值進行精細化仿真，獲得更精確的取值。

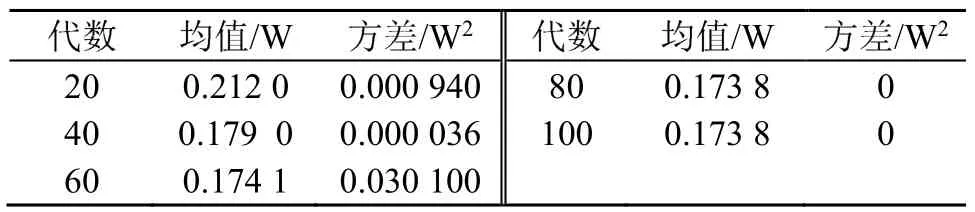
表2 種群繁殖代數的影響(N=200)Table 2 The influence of the generations of population reproduction (N=200)

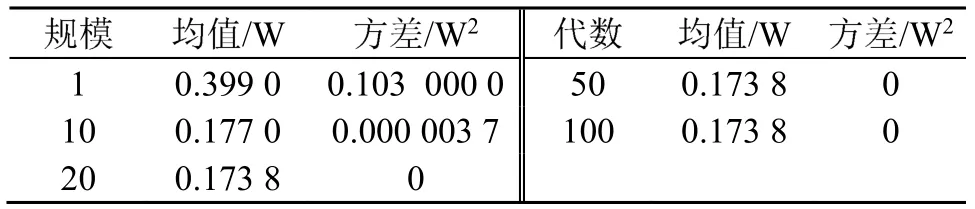
表3 粒子群規模的影響(MG=100)Table 3 The influence of particle swarm size (MG =100)

5 結 論

本文針對水聲通信網絡能量優化問題，通過改進水聲通信網絡模型，采用事件觸發的方式觸發網絡進入路徑優化階段，從而降低了網絡優化階段的額外的能量消耗。并通過在網絡路徑優化階段引入改進的粒子群算法建立優化算法，尋優獲得網絡中各個節點的最優信息傳輸路徑，以降低網絡節點的總功耗。仿真結果表明，本文所提優化方法能有效降低網絡節點總功耗，延長首個節點死亡時間，減緩網絡中節點死亡速率，從而減緩了網絡有效覆蓋面積隨著網絡運行而減小的速率。