一種信標水聲定位的改進擴展卡爾曼濾波算法
劉建波,韓樹平,徐景峰,楊 剛
(海軍潛艇學院,山東青島 266000)
0 引 言
信標利用水聲信號對水下航行器提供導航定位服務,主要利用的是距離和方位信息。關于水聲純距離定位導航方面有較多的研究[1-4];文獻[5]將水聲通信與定位導航結合,利用單程傳播時延實現距離估算和定位導航。水聲測距誤差受多種因素影響,一般并不滿足高斯噪聲假設,文獻[6]分析了影響水聲測距系統誤差的各種因素,文獻[7-8]提出了基于色噪聲條件下的改進卡爾曼濾波方法;文獻[9-10]等提出了基于乘性噪聲條件下的濾波定位算法;文獻[11-12]等討論了迭代初值對濾波的影響,提出了迭代初值的選取辦法。
針對水聲測距時噪聲模型失配的問題,本文提出了一種緩變測距偏差模型,將測距噪聲分為高斯分量和緩變非高斯分量,當兩次觀測間隔較小時,假定緩變非高斯分量不變。基于此,提出一種改進的擴展卡爾曼濾波(Improved Extended Kalman Filter, IEKF)算法,研究了IEKF算法的初值選取方法。仿真實驗和湖試結果表明,IEKF算法能夠對測距偏差進行跟蹤補償,在復雜噪聲條件下定位精度明顯優于常規擴展卡爾曼濾波(Extended Kalman Filter, EKF)算法。
1 基于緩變測距偏差的改進EKF
1.1 基于緩變測距偏差的改進EKF(IEKF)算法
水下純距離導航定位時,水聲測距誤差與多種因素相關。利用傳播時延進行距離估計,距離誤差dr/r=dt/t+dc/c,時延測量誤差dt與信號帶寬和信噪比有關,與距離無關,在遠距離測量時對測距誤差影響較小。聲速誤差與實際水文環境有密切關系,即使利用聲速剖面對有效聲速進行修正,海底地形失配以及洋流等因素也會導致有效聲速在不同方向和距離上的變化,增大聲速誤差。在收發雙方距離較遠時,聲速在水平方向上也有可能發生較大變化,增大聲速誤差。一般來說,水聲測距誤差與距離成正比,距離越遠,誤差越大,但是在不同方向上,受洋流、地形等環境影響,聲速誤差規律可能存在不同。
假設測距噪聲ξk由兩部分組成:ξk=ηk+υk,其中ηk是零均值高斯噪聲,υk是緩變的測距偏差,由于實際物理環境具有連續性,當前后兩次觀測時間間隔較短、距離較近時,認為υk的變化較小,υk=υk?1。
根據以上假設,對EKF算法進行改進,將狀態向量進行擴展如下:Xk=[xkykυk]T,并將狀態方程和觀測方程修改為[13]
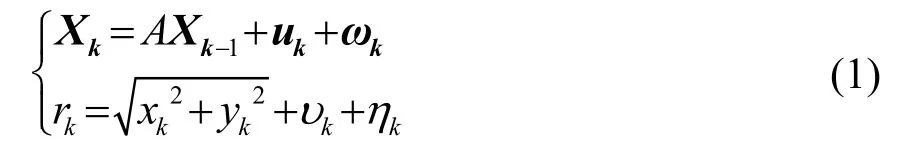
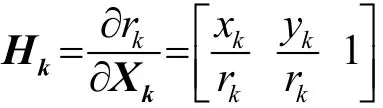

狀態向量先驗協方差陣P可初始化為單位陣。狀態噪聲協方差陣,其中主要取決于控制輸入量uk的精度,水下平臺一般采用航跡推算(Dead Reckoning, DR)或慣性導航系統(Inertial Navigation System, INS)獲取uk,與可根據經驗確定;對于,在兩次觀測間隔距離較近時,vk的噪聲主要由狀態誤差與引起,,當兩次觀測間隔較大時,可以適當增大。
1.2 改進EKF濾波的初值確定方法
一般而言,二維純距離定位跟蹤系統滿足可觀測性條件[14-15],但是機動路線和迭代初值等因素對解算收斂速度和精度有較大影響。IEKF算法與經典EKF算法相比,已知信息量不變,而擴展了狀態向量,增加了未知信息υk,對算法收斂性能有不利影響,仿真顯示,IEKF算法對初值比較敏感。當初值誤差較小時,跟蹤性能較好,系統很快進入穩定跟蹤狀態,當選取的初值誤差較大時,跟蹤性能較差,需要經過長時間的震蕩才能趨于穩定。
為了減小初值對IEKF跟蹤性能的影響,在進入迭代跟蹤之前,不僅需要對目標進行預定位,而且需要對預定位結果進行評估,確保預定位結果具有足夠的精度,才能使后續濾波盡快收斂。
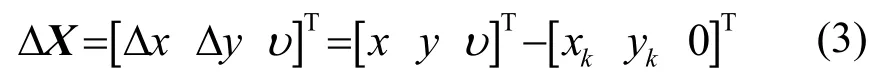
由于測距偏差υk的存在,前述估計結果仍有可能存在較大偏差,為了進一步提高預定位精度,并定量分析預定位誤差的大小,對觀測方程進行線性化近似,假設測距偏差在預定位期間不變,觀測方程可表示為
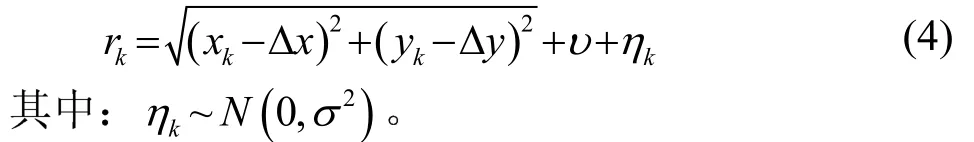
設水下平臺與浮標的距離較遠,dr/r?1,將式(4)泰勒展開并保留一階項可得:
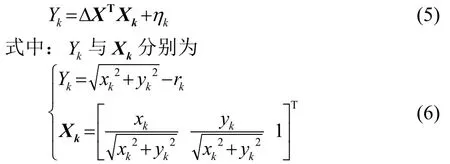
假設從觀測伊始至完成預定位共獲得k組觀測數據ri,i=1,2,…k,利用[xkyk]T反推平臺歷史位置,獲得如下線性回歸方程:

其中:Y=[Y1Y2…Yk]T,X=[X1X2…Xk]T,η~N(0,σ2),Xi、Yi與[xiyi]T以及ri的關系與式(6)形式相同。設式(7)中的線性回歸方程的最小二乘解為


式中,Var(?)表示求向量的協方差。根據文獻[16]中定理,預定位均方誤差可表示為
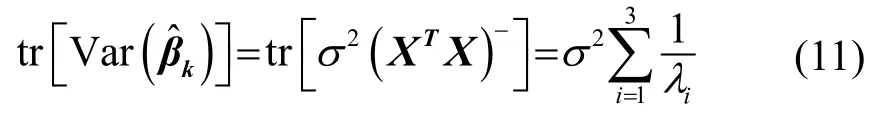

當α?1時,預定位結果誤差較大,不足以采信,當α≈1時,預定位誤差與測距噪聲誤差相近,可以作為后續濾波的初值。
2 仿真實驗與湖試結果分析
2.1 仿真結果與分析
仿真實驗中,水下平臺繞浮標運動,每隔一定時間向靠近浮標的方向轉向一次,轉向角度隨機,水下平臺一個典型的軌跡如圖1(a)所示。測距誤差ξk由高斯白噪聲ηk和緩變測距偏差vk組成。其中E(ηk)的均值為0、方差為5 m。υk分為兩部分,一是聲速誤差引起的與距離成正比的乘性偏差γrk,γ為聲速誤差,一般不超過 1%;二是緩變隨機偏差μk+ρ,μk為零均值隨機偏差,可以通過低通濾波器對高斯白噪聲濾波進行模擬,ρ為隨機偏差的均值,仿真測距誤差如圖1(b)所示。
預定位精度因子α隨觀測數據點數的變化如圖2所示。

圖1 水下平臺航跡與測距誤差Fig.1 Track and ranging error of underwater platform
在圖1所示軌跡下,預定位精度因子隨觀測點數據的增加迅速下降,在獲得約200組數據后降為1,此時平臺相對浮標的方位變化約90°。
圖3顯示了初值偏差對常規EKF與IEKF定位跟蹤的影響,圖3(a)迭代初值與真值的距離誤差為150 m,圖3(b)迭代初值與真值的距離誤差為30 m。結果顯示,對于傳統EKF算法,定位誤差約100 m,受迭代初值誤差影響較小。對于IEKF算法,當初值誤差150 m時,1 000組數據后定位誤差約40 m,測距偏差跟蹤結果震蕩,2 000組數據后漸趨穩定,當初值誤差30 m時,800組數據后定位跟蹤誤差收斂至20 m,測距偏差跟蹤穩定。

圖2 預設定位精度隨觀測數據的變化關系Fig.2 Variation of pre-positioning precision with observed data points
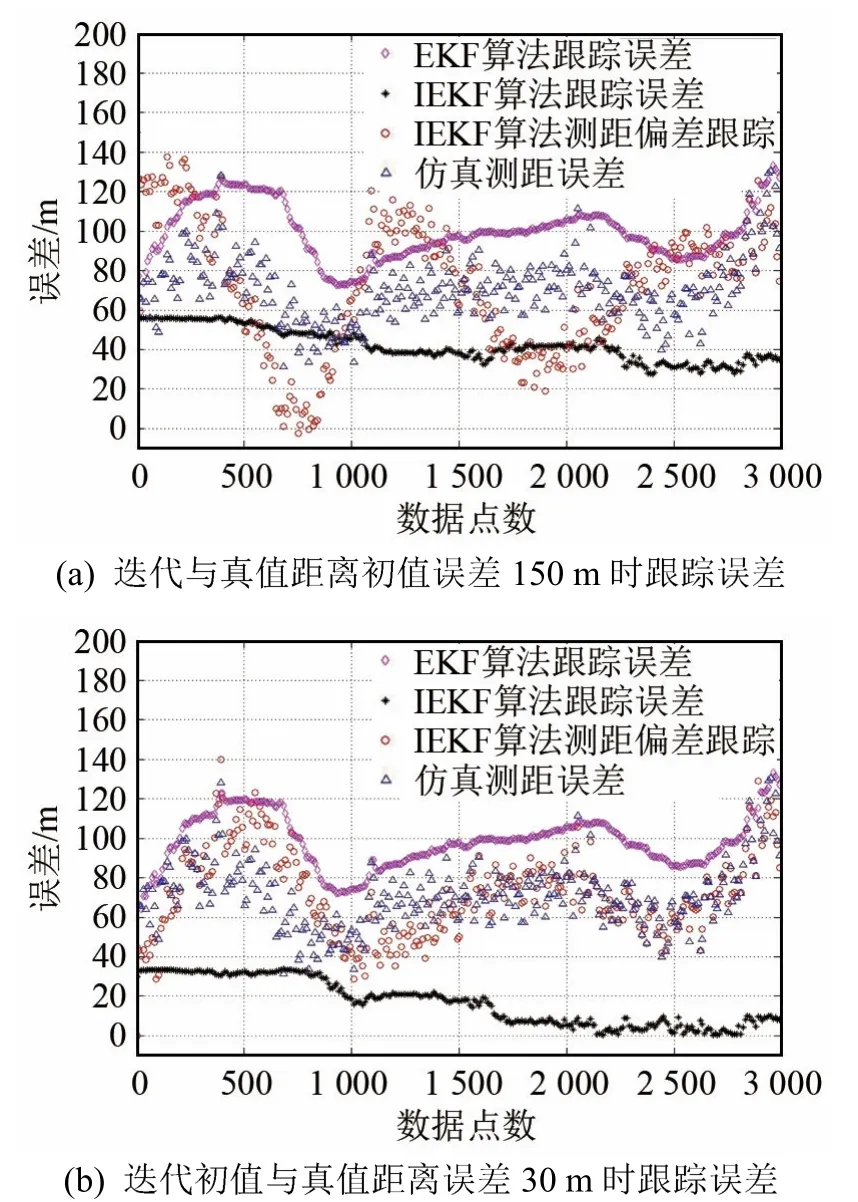
圖3 預設定位精度對跟蹤算法的影響Fig.3 The influence of the pre-positioning precision on tracking algorithm
圖4顯示了經過預定位后的跟蹤結果,在預定位精度因子α低于2時進行預定位。結果顯示,利用350組數據完成預定位后,定位精度約20 m,測距偏差跟蹤穩定。與圖3相比可以看出,在缺乏精確的位置先驗信息時,預定位可以使跟蹤過程更快收斂。
圖5顯示了基于緩變測距偏差的IEKF算法和基于乘性噪聲的EKF算法[10]結果對比,可以看出兩者定位誤差約20 m,與常規EKF算法相比具有更高的精度。
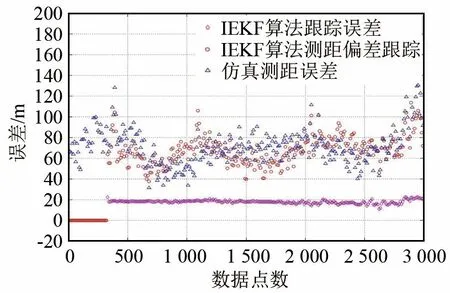
圖4 預設定位處理后的IEKF算法的跟蹤結果Fig.4 The IEKF tracking result after pre-positioning processing
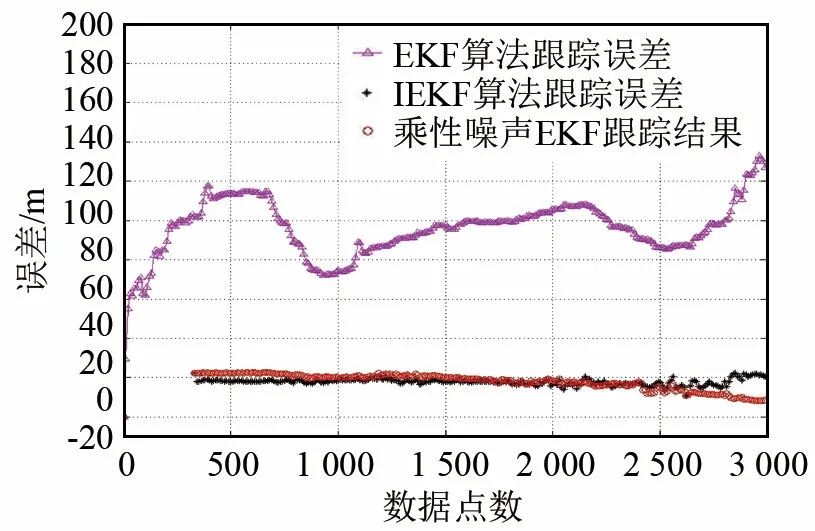
圖5 基于乘性噪聲的EKF算法和基于緩變測距偏差的IEKF算法的跟蹤結果對比Fig.5 Comparison of tracking results between the multiplicative noise based EKF and the slow variable ranging deviation based IEKF results
為了比較IEKF算法和基于乘性噪聲的EKF算法的計算結果,在測距誤差ξk總方差固定的條件下,為乘性偏差γrk和隨機偏差μk分配不同比例的方差,比較兩種算法穩定跟蹤性能,不同條件下300次蒙特卡洛仿真結果如圖6所示。當噪聲總方差固定時,IEKF算法性能比較穩定,與γrk和μk的相對大小基本無關,而基于乘性噪聲的EKF算法性能與γrk和μk的相對大小有關,隨機偏差μk方差在ξk總方差中占比小于25%時,基于乘性噪聲的EKF算法表現優于IEKF算法,反之則IEKF算法性能更優。注意γrk方差與聲速誤差γ和距離rk的變化有關。在距離變化較小、能夠獲取實時聲速剖面、對聲線彎曲進行精確補償的條件下,乘性偏差γrk較小,受海底地形、洋流等環境因素影響的隨機偏差μk較大,IEKF算法具有更好的性能。

圖6 噪聲總方差恒定時兩種算法跟蹤性能對比Fig.6 Comparison of tracking performance of the two algorithms for a certain total variance of noise
2.2 湖試結果與分析
為了檢驗IEKF算法的有效性,利用2018年某水域進行的測距定位試驗數據對算法進行了驗證,分別利用 EKF算法、IEKF算法和乘性噪聲 EKF算法進行定位。試驗中用兩條船分別搭載水聲信號發送和接收系統,并實時記錄收發船只全球衛星導航系統(Global Navigation Satellite System, GNSS)位置。試驗中,發射系統將自身GNSS數據利用水聲擴頻通信方法發送至接收系統。接收系統利用自身GNSS數據推算自身位移,模擬DR或INS系統的位移控制量ukr,利用發射系統 GNSS數據推算發射系統位移信息uks,整個系統可等效為固定浮標和移動平臺的定位跟蹤問題,位移控制輸入量uk=ukr?uks。
圖 7顯示了試驗期間收發船只位置和相對態勢。受試驗場地和條件所限,試驗期間,信號發射系統在四個方位上各發射一組信號,沒有進行長時間連續機動發射,其中第1、2組相對方位約50°,第3、4組相對方位約320°,方位差約90°。
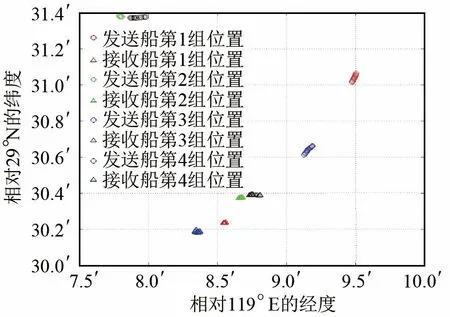
圖7 收發船只的全球衛星導航系統(GNSS)相對位置Fig.7 GNSS relative positions of transmitting and receiving boats
圖8顯示了4組信號的GNSS距離和水聲測距結果。各組數據收發距離相近,測距噪聲各不相同,與距離的關系較小。
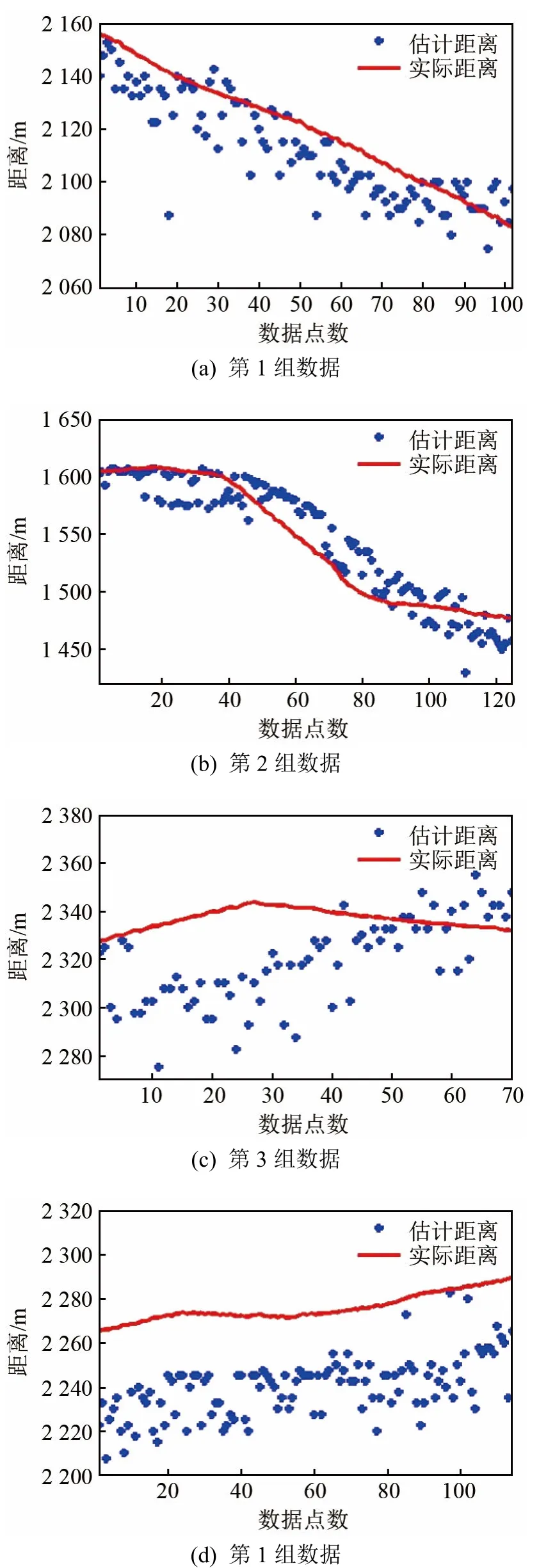
圖8 收發船只實際距離與估測距離Fig.8 The actual and estimated distances between the transmitting and receiving boats
試驗數據處理結果如圖9所示。圖9(a)顯示了不同算法定位結果,圖9(b)顯示了IEKF算法估算的υk與實際測距誤差的對比。
從圖9可以看出,IEKF算法經過預定位后,定位誤差約10 m,EKF算法定位誤差收測距噪聲影響,在10~40 m范圍內波動,IEKF算法性能明顯優于EKF算法,能夠較好地跟蹤和補償測距緩變偏差。
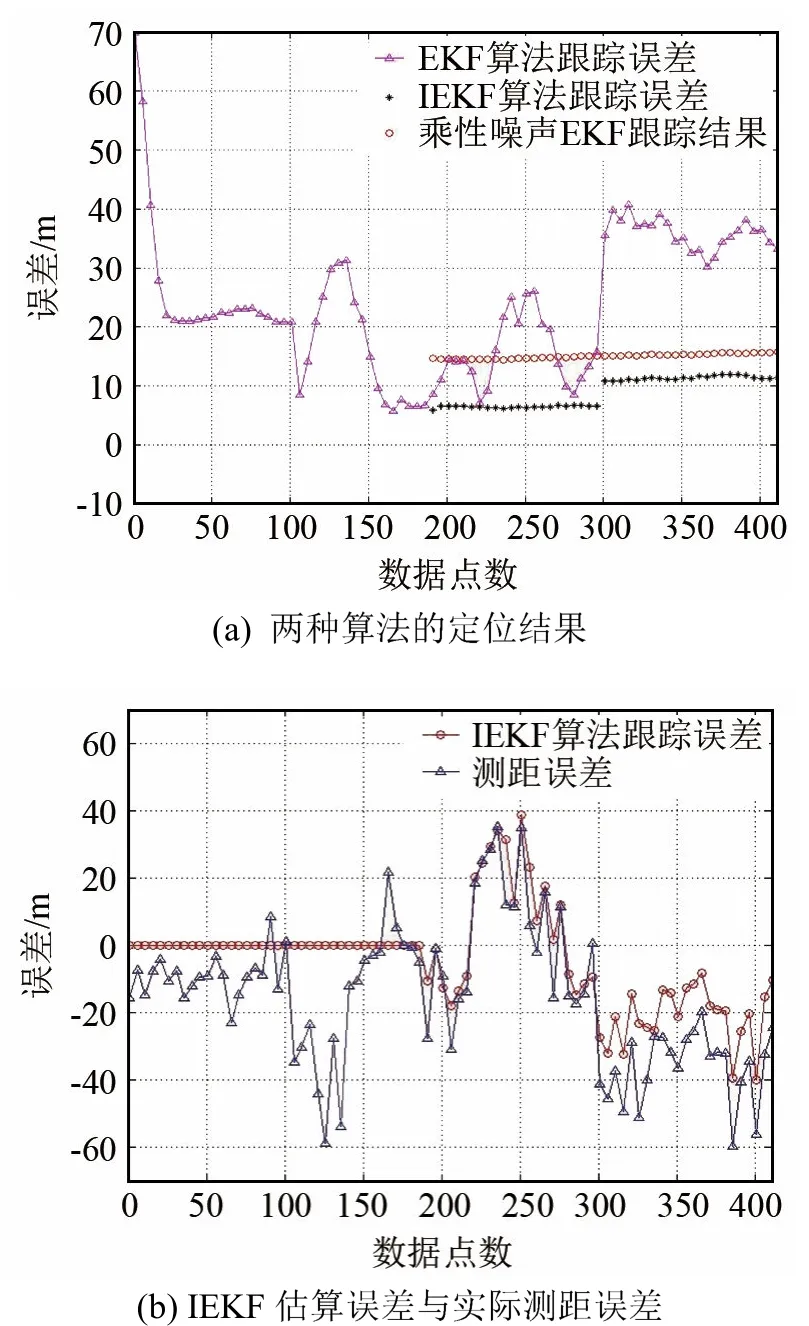
圖9 湖試數據處理結果Fig.9 The processing results of lake trial data
3 結 論
本文提出了一種基于緩變測距偏差的改進EKF(IEKF)算法,將水聲測距誤差分為緩變偏差和零均值高斯噪聲兩部分,并通過對緩變偏差的跟蹤與補償,減小測距噪聲模型失配對EKF的影響。仿真實驗和湖試結果表明,本文提出的迭代初值選取方法能夠使IEKF算法實現對緩變測距偏差的跟蹤補償,當緩變隨機偏差在總方差中的占比較大時,性能優于基于乘性噪聲的EKF算法。

