交叉滯后路徑分析在變量因果時序關系研究中的應用*

周廣帥 范冰冰 王春霞 游頂云 劉言訓 薛付忠 陳 偉 張 濤△

【提 要】 目的 介紹交叉滯后路徑分析原理及其在變量間因果時序關系研究中的應用。方法 交叉滯后路徑分析模型基于交叉滯后面板設計，估計的路徑系數具有明確的時間順序關系，滿足因果推斷中“因在前果在后”的時序性要求。利用健康隨訪數據構建體重指數(BMI)與血尿酸(UA)的交叉滯后路徑分析模型，探索BMI和UA的因果時序關系。結果 調整混雜因素后，基線BMI到隨訪時UA的路徑系數(ρ2=0.060，P<0.001)明顯大于基線UA到隨訪時BMI的路徑系數(ρ1=-0.009，P=0.056)，且兩系數間的差異具有統計學意義(ρ2>ρ1，P<0.001)。在時間順序上BMI增加先于UA升高發生。結論 BMI增加可能是高尿酸血癥的原因，交叉滯后路徑分析模型可以有效的識別變量間的因果時序關系。

實際研究中，通常利用因果圖(casual diagram)的方式直觀地標識危險因素之間的相關或因果關系，從而清晰地表達混雜效應、中介效應等多種因果推斷的關鍵概念[1]。如圖1所示的因果圖模型，X為解釋變量，Y為反應變量，Z為另一個解釋變量。虛線雙箭頭表示存在關聯，實線箭頭表示有因果關系[2]。若X→Z則為中介效應模型，反之為混雜效應。因此，確定X和Z之間的因果方向是區分混雜和中介的關鍵。

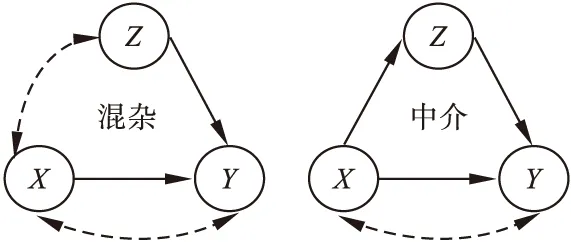
圖1 混雜和中介的因果圖模型示意圖

交叉滯后路徑分析(cross-lagged path analysis)是利用縱向隊列中兩個及以上的面板數據，探索兩個變量間因果時序關系(temporal sequence)的一種統計分析方法[3]。貝葉斯網絡可采用有向無環圖表示因果網絡，被廣泛應用于因果機制的發現和因果推斷中，但其通常是基于橫斷面數據。交叉滯后路徑分析的優勢是結合了交叉滯后面板設計(cross-lagged panel design)，估計的路徑系數具有明確的時間順序關系，符合“因在前果在后”的因果推斷原則，常用于變量間因果時序關系的研究[4-7]。

本文將介紹交叉滯后路徑分析的基本原理和分析步驟，并通過體重指數(BMI)與血尿酸(UA)因果時序關系的研究實例介紹該方法的實際應用。

交叉滯后路徑分析

交叉滯后路徑分析在交叉滯后面板設計基礎上，研究兩變量間的因果時序關系，在數據上要求兩個及以上的面板數據，其模型示意圖如圖2所示。假設任意兩變量分別為X和Y，其基線水平分別為X1和Y1，隨訪水平分別為Xt和Yt。其中β1和β2為自相關系數(autoregressive coefficient)，表示隨訪測量(Xt或Yt)與基線測量(X1或Y1)的自相關關系；r1為同步相關系數(synchronous coefficient)，是基線X1與Y1的相關系數；ρ1和ρ2為cross-lagged路徑系數(cross-lagged path coefficient)。需注意的是，交叉滯后路徑分析模型中并不包含Xt→Yt和Yt→Xt的因果路徑，即Xt和Yt之間不存在同步效應。否則，模型中需要估計的參數個數將超過已有的方差和協方差數量，模型將無法識別[8-9]。

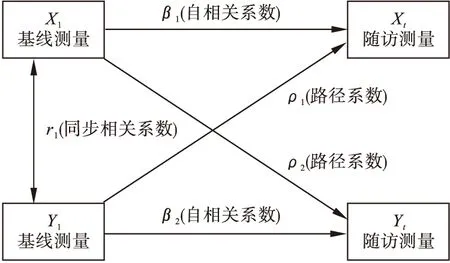
圖2 交叉滯后路徑分析模型示意圖

在路徑分析框架下，交叉滯后路徑分析模型的形式如下：

Xt=α1+β1X1+ρ1Y1+e1

Yt=α2+β2Y1+ρ2X1+e2

其中α1和α2為模型截距，e1和e2為模型殘差。

路徑系數ρ是交叉滯后路徑分析進行因果時序關系推斷的依據，其含義為：在控制了因變量基線狀態(如Y1)后，自變量(如X1)基線測量結果對因變量(如Yt)的影響，即Yt=α2+β2Y1+ρ2X1+e2。該模型經轉換可表示為Y的動態變化同基線X1和Y1的回歸形式，即ΔY=(Yt-Y1)=α2+(β2-1)Y1+ρ2X1+e2。計算的路徑系數ρ在時間上具有明確的先后順序(X1→Yt，Y1→Xt)。

通過路徑系數ρ1和ρ2的比較可以確定變量間的因果時序關系，包含以下四種情況：若ρ1=0，ρ2=0，則X，Y間無因果時序關系；若ρ1≠0，ρ2=0，且兩系數差異顯著，則兩變量為Y→X的單向因果時序關系；若ρ1=0，ρ2≠0，且兩系數差異顯著，則兩變量為X→Y的單向因果時序關系；若ρ1≠0，ρ2≠0，則X，Y為相互調控的雙向因果時序關系，此時若ρ1>ρ2且兩者差異顯著，可進一步確定主要因果時序效應為Y→X，反之則為X→Y。

研究實例

肥胖和高尿酸血癥是心腦血管疾病的危險因素，大量流行病學和臨床研究發現肥胖和高尿酸血癥存在顯著的相關性，然而其因果時序關系仍然存在爭議。通常認為體重指數(BMI)增加會導致高尿酸血癥，但也有研究發現血尿酸(UA)水平高的人群更易患有肥胖[10-12]。此外，基礎研究表明尿酸可引起細胞內脂肪累積，導致體重增加[13]。本文將通過交叉滯后路徑分析探討BMI和UA之間的因果時序關系。

本研究基于山東某三甲醫院2004到2015年的健康隨訪數據，選取基線年齡≥20歲，體檢記錄中包含兩次及以上BMI和UA測量的體檢參與者。由于數據中不包含高尿酸血癥的相關治療信息，為防止服藥對尿酸水平的影響，排除了患有高尿酸血癥的人群。本研究最終共納入15348名對象，選取其基線和最后一次隨訪數據進行交叉滯后路徑分析。研究對象的基線與隨訪特征如表1所示，其中男性9578人，女性5770人，基線平均年齡為39.68歲，平均隨訪時間為3.36年。

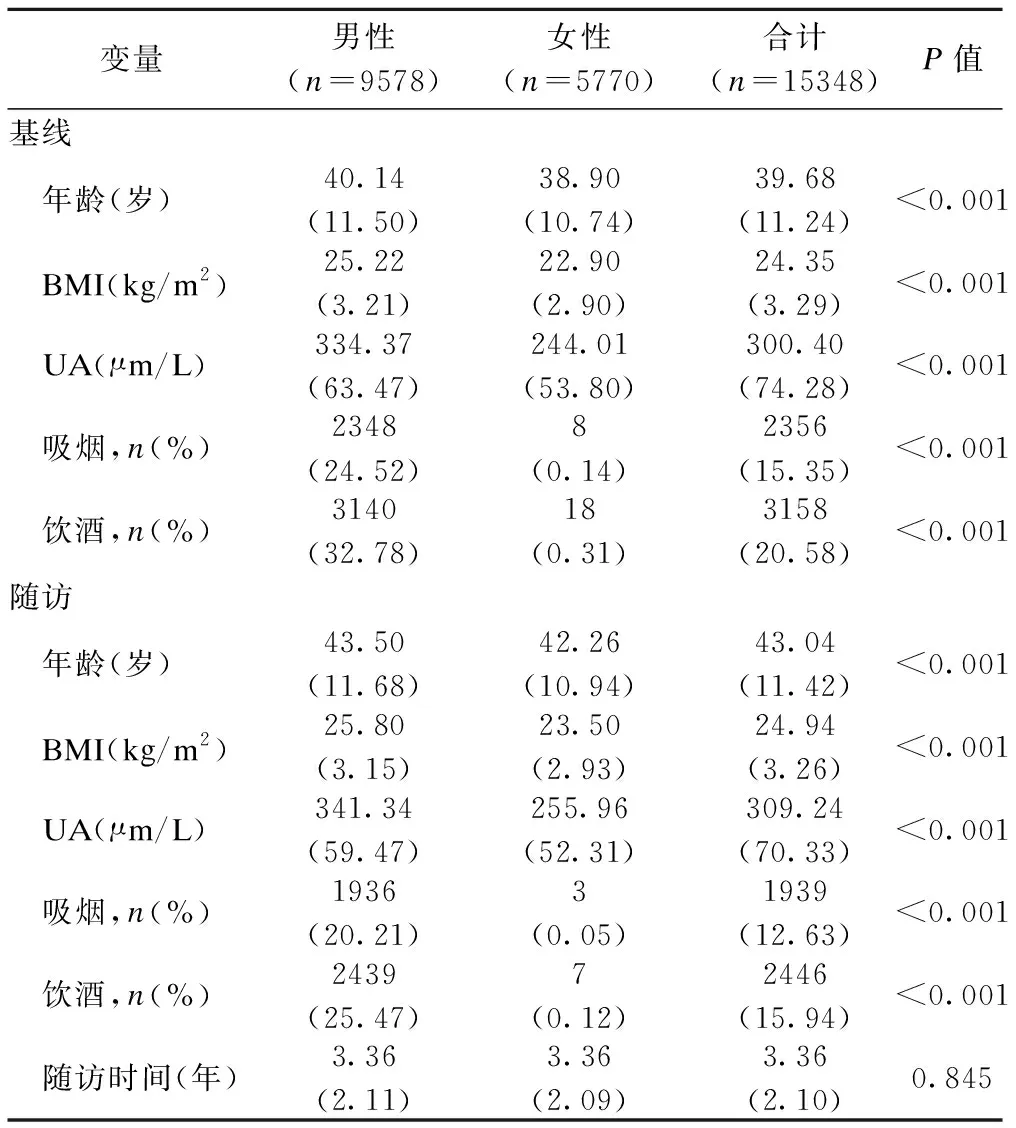
表1 研究隊列特征

交叉滯后路徑分析的建模步驟

交叉滯后路徑分析作為路徑分析的一種，可使用結構方程模型的分析軟件建立模型，如：LISREL、AMOS、SAS中CALIS過程步、R中sem包、lavaan包等。

1.數據預處理

交叉滯后路徑分析前，為控制潛在的混雜效應和消除量綱影響，需對研究變量進行回歸殘差分析，具體步驟為：(1)構建研究變量與混雜因素(如：年齡、性別、吸煙、飲酒、隨訪時間等)的多元回歸方程；(2)對上述方程取殘差，并進行Z轉化的標準化處理。

2.計算協方差矩陣

結構方程模型又稱協方差結構模型，其分析軟件多以協方差矩陣為基礎開始模型擬合，如LISREL，sem包等。此外一些結構方程模型分析軟件也可以直接使用原始數據進行模型分析，如：AMOS、CALIS過程步、lavaan包等。交叉滯后路徑分析模型在預處理時已將研究變量標準化，其協方差矩陣與相關系數矩陣相同。

3.模型構建

(1)根據現有研究確定各時點BMI與UA間的路徑方向，建立如圖3所示的交叉滯后路徑分析模型，其結構方程組如下：

BMIt=β1BMI1+ρ1UA1+e1

UAt=β2UA1+ρ2BMI1+e2

上述方程組中基線BMI1、基線UA1、隨訪BMIt、隨訪UAt的協方差矩陣為[14]：

∑=

其中r1為基線BMI、基線UA的同步相關系數；re為e1、e2的相關系數。

(2)通過結構方程模型分析軟件對上述模型進行參數估計。本研究采用lavaan包直接對原始數據進行模型分析。具體代碼如下，#號后文字是對代碼的注釋：

install.packages(“lavaan”)#安裝lavaan包

library(lavaan)#載入lavaan包

model1<-"BMIt～a1*BMI1+b1*UA1，

UAt～a2*UA1+b2*BMI1，

BMI1～～r1*UA1，

BMIt～～0*UAt"#輸入模型公式

result<-sem(model=model1，data=usedata)#模型求解

summary(result)#查看模型結果

fitMeasures(result，c(“rmr”，“cfi”))#查看模型擬合情況

其中r1對應同步相關系數r1，a1、a2分別對應自相關系數β1和β2，b1、b2分別對應路徑系數ρ1和ρ2；使用sem函數進行求解，model為需要輸入的模型結構，data為分析所用的數據，此處usedata已經過預處理控制了混雜因素的影響；使用summary查看上述分析結果，使用fitMeasures查看模型擬合情況。

Lavaan包中默認使用極大似然法(maximum likelihood，ML)進行參數估計。其原理為通過迭代計算使模型隱含的協方差矩陣即“再生矩陣”與樣本協方差矩陣間“距離”最小，得到模型最優解。ML屬于完全信息方法，具有無偏、一致、尺度不變和漸進有效性的優點，是當前結構方程模型最常用的參數估計方法，其假設為變量服從多元正態分布[14]。

(3)判斷模型參數估計是否合理，并通過擬合指數評價模型擬合情況。

常用的模型擬合指數有CFI(comparative fit index)和RMR(root mean-square residual)。其中CFI反映當前假定模型與變量間相互獨立的虛模型(最不理想模型)的差異程度，具有不易受樣本量影響，小樣本時表現良好的優點，其值越大擬合越好；RMR則是基于假定模型整體殘差的模型擬合指數，具有對誤設模型較為敏感的優點，其值越小擬合越好。當CFI>0.90且RMR<0.05時表示模型擬合良好[4，15]。

(4)通過Fisher Z′ test對路徑系數進行比較，確定主要因果時序效應。

實例分析結果

調整年齡、性別、吸煙、飲酒、隨訪時間后，BMI和UA在基線與隨訪時的相關系數和散點圖如圖4所示，其中基線UA與隨訪UA的相關系數為0.615，基線BMI與基線UA、隨訪BMI的相關系數分別為0.246、0.831，圖中所有的相關系數均具有統計學意義。

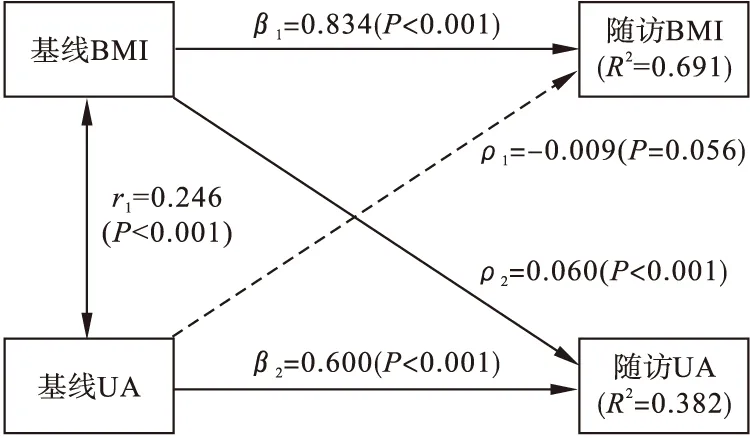
圖3 BMI與UA的交叉滯后路徑分析模型

BMI與UA的交叉滯后路徑分析模型結果如圖3所示，調整年齡、性別、吸煙、飲酒、隨訪時間后，由基線BMI到隨訪UA的路徑系數ρ2(ρ2=0.060，P<0.001)明顯大于由基線UA到隨訪BMI的路徑系數ρ1(ρ1=-0.009，P=0.056)，且兩系數間差異具有統計學意義(ρ2>ρ1，P<0.001)。BMI和UA兩次測量間的自相關系數分別為0.834和0.600。模型擬合指數CFI和RMR分別為0.979和0.027，提示當前模型擬合良好。

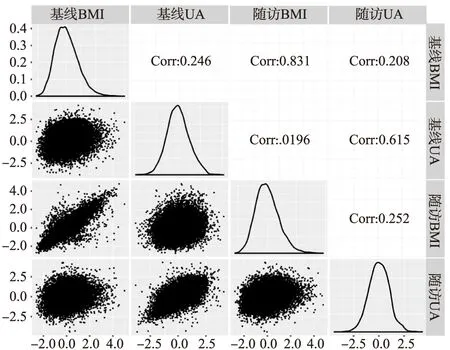
圖4 基線與隨訪的BMI、UA相關系數和散點圖

如圖5所示，調整年齡、性別、吸煙、飲酒后，隨著基線BMI四分位數的增加UA的年變化率逐漸升高，且增長趨勢具有統計學意義；而隨著基線UA四分位數的增加BMI的年變化率基本保持不變，增長趨勢沒有統計學意義。圖5結果與圖3中交叉滯后路徑分析結果一致。

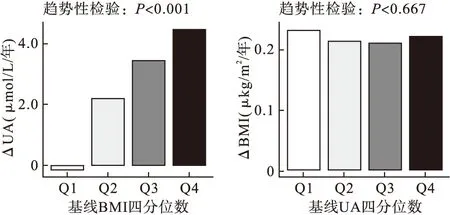
圖5 不同基線四分位數下UA、BMI的年變化率

此外，本文選取隨訪隊列中體檢三次及以上的4797名參與者的隨訪信息，構建了三斷面交叉滯后路徑分析模型，進行了敏感性分析。模型結果如圖6所示，調整混雜因素后，在不同斷面間均存在的單向因果時序關系(ρ2=0.046，P<0.001；ρ4=0.061，P<0.001)，與圖3兩斷面模型結果一致。CFI=0.931，RMR=0.052提示當前模型擬合良好。綜上，可以認為BMI與UA間因果時序方向為BMI→UA，即在時間順序上BMI增加先于UA水平升高發生，BMI增加可能是導致高尿酸血癥的原因。

討 論

變量間的時序關系是流行病學中進行因果推斷的重要原則之一，也是因果圖模型中確定節點間箭頭方向的基礎。交叉滯后路徑分析是利用縱向隊列中兩個及以上面板數據，探索兩變量間因果時序關系的方法，其估計的路徑系數具有明確的時間順序關系，符合“因在前果在后”的因果推斷原則，為進一步的因果關系探索提供了依據。

交叉滯后路徑分析需滿足以下假設：(1)變量服從多元正態分布，當違背正態性假定時，使用ML法的模型參數標準誤將被低估，增大I型錯誤風險，此時可通過變量轉換，或者通過S-B調整的ML法、漸進自由分布法、自助抽樣法等進行模型擬合[14]；(2)人群內部一致性，交叉滯后路徑分析關注總體層面的平均因果效應，未充分考慮個體間差異，當研究變量個體變異較大時可能影響模型結果[16]；(3)隨訪間隔接近真實因果效應時間，變量間的相互作用常需一定發生時間，如果隨訪間隔太短或太長，因果效應可能尚未發生或已經消失，影響時序關系判斷，模型選取的隨訪間隔應盡量接近真實的因果效應時間，但實際應用中受限于現有數據，該假設往往容易被違背[17]。此外需注意的是交叉滯后路徑分析仍借助常規回歸方法控制混雜效應，模型結果可能受到未知混雜影響。另一方面，交叉滯后路徑分析屬于驗證性分析，模型假定的因果方向均應來自現有人群或理論研究。

兩變量兩斷面交叉滯后路徑分析是該模型最基本的形式，當包含三個或者更多面板時，可構建包含多個隨訪間隔的交叉滯后路徑分析模型，通過比較各隨訪期內的路徑系數，探索不同時點下變量間因果時序方向和強度的變化規律[18]。多斷面模型中，每個面板的隨訪人群均應處于相同年齡段或生命歷程階段(如：兒童發育階段、女性絕經狀態等)。其中三斷面模型要求三個隨訪斷面均處于相同生命歷程階段(如：均為成年期)，常用于兩斷面模型的敏感性分析，以檢驗隨訪間隔改變對模型結果的影響。本文實例分析部分BMI與UA的三斷面交叉滯后路徑分析模型與兩斷面模型結果一致，均提示BMI增加是導致高尿酸血癥的原因。多斷面模型的模型構建和求解過程與兩斷面模型類似，鑒于文章篇幅不再展開。此外，隨著模型發展交叉滯后路徑分析已衍生多種模型形式，關注較多的有RI-CLPM(random-intercept cross-lagged panel analysis model)、ALT-SD(autoregressive latent trajectory model with structured residuals)等，前者通過在模型中引入截距因子(潛變量)，為控制個體間差異對變量間真實時序關系的影響提供了可能[16]；后者則將交叉滯后路徑分析與潛變量增長曲線模型結合，使模型在估計變量間因果時序關系的同時也可獲得變量的總體變化軌跡，擴展了交叉滯后路徑分析模型的應用范圍[19]。