ARIMA乘積季節模型與GRNN模型在猩紅熱發病預測中的比較*

濰坊醫學院公共衛生學院(261053) 馮佳寧 肖宇飛 王曉璇 孫 娜 許小珊 王素珍 石福艷

【提 要】 目的 探尋適合猩紅熱發病的預測模型，為猩紅熱的預防和控制提供科學依據。方法 利用全國2011年1月至2018年12月的猩紅熱月發病率，通過R 3.6.1軟件建立求和自回歸移動平均(autoregressive integrated moving average，ARIMA)乘積季節模型和軟件Matlab 9.1創建廣義回歸神經網絡(generalized regression neural netword，GRNN)，通過R2比較模型的擬合效果，平均相對誤差比較模型預測能力，并對2019年1月-6月發病率進行預測。結果 創建的ARIMA(2，1，2)(0，1，1)12乘積季節模型平穩R2為0.336，預測2019年1-6月的發病率(1/10萬)分別為0.637、0.274、0.377、0.579、0.910和0.937，GRNN模型的R2為0.823，預測2019年1-6月發病率(1/10萬)分別為0.626、0.178、0.321、0.445、0.789和0.774。模型的平均相對誤差分別為31.1%和20.3%。結論 ARIMA模型和GRNN模型均能對猩紅熱發病率進行預測，但GRNN模型預測能力較前者更優。

猩紅熱是兒童常見的急性呼吸道傳染病，在我國屬于法定報告的乙類傳染病[1]。在對猩紅熱的發生、流行及其變化趨勢進行預測時，通常采用求和自回歸移動平均(autoregressive integrated moving average，ARIMA)模型[2-4]，但是傳染病的相關數據往往是不穩定的，易受自然和社會因素的影響而發生不同的變化，這類數據通常具有線性趨勢和非線性關系，只通過線性模型信息提取不夠充分。人工神經網絡(artificial neural network，ANN)以其獨特的并行結構、自適應、自組織、較強的容錯性、穩健性等特點和獨特的信息處理方法，在時間序列預測領域得到了廣泛的應用[5-6]。目前在預測上應用較多的BP神經網絡模型，在訓練時存在收斂速度慢和容易出現局部最優解的缺點。而廣義回歸神經網絡(generalized regression neural network，GRNN)基于徑向基神經元和線性神經元建立，對樣本數據要求不高，也可以有很好的預測效果，尤其對非線性問題處理效果較好。

本研究采用我國2011年1月至2018年12月的猩紅熱月發病率進行分析，分別建立ARIMA乘積季節模型和GRNN模型，并對兩種模型的預測效果進行比較，從而為猩紅熱發病預警提供更優模型，在今后的預防決策中提供科學指導。

資料與方法

1.猩紅熱發病資料

本研究資料為中國疾病預防控制中心(http：//www.chinacdc.cn/)報告系統發布的2011年1月至2018年12月猩紅熱月發病人數，計算發病率所用的人口數來自中國統計年鑒。

2.模型原理與方法

(1)ARIMA模型建立

ARIMA 模型是由美國統計學家Box和英國統計學家Jenkins提出的，ARIMA(p，d，q)模型中p，d，q分別表示自回歸階數、差分階數、平均移動階數[7]。ARIMA 模型記作：

(2)GRNN模型建立

GRNN是一種前饋式神經網絡模型，是在觀測樣本中得到自變量與因變量的聯合概率密度函數后，直接計算因變量對自變量的回歸值[10]。GRNN 只需要人工調節光滑因子這一個參數，所以其結構的搭建比其他網絡簡單。其結構如圖1所示，包括輸入層、模式層、求和層與輸出層等4層神經元。對應網絡輸入X=[x1，x2，…，xn]T，其輸出為Y=[y1，y2，…ym]T。

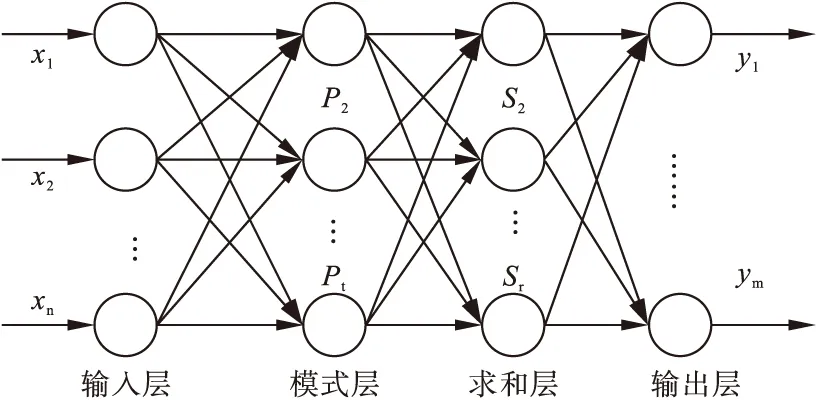
圖1 廣義回歸神經網絡結構圖

GRNN模型建立可簡單分為兩步：①確定神經網絡的輸入和輸出數據、訓練樣本和預測樣本。本研究選擇的輸入數據為2011年至2017年猩紅熱月發病率，輸出數據為2013年至2018年猩紅熱月發病率，訓練樣本選擇2017年和2018年的1-6月發病率，對2019年1-6月的發病率預測。②創建GRNN模型。模型創建通過MATLAB中程序代碼net=grnn(P，T，spread)實現，其中P為輸入樣本，T為輸出樣本，spread為光滑因子。預測程序代碼為y=sim(net，p)，p表示預測集的輸入數據，y表示預測結果。通過交叉驗證法獲得最優光滑因子spread，使函數的逼近誤差最小[11]。選擇2011年-2017年任意6個月的發病率作為測試集數據，最小均方誤差MSE對應的spread即為最優光滑因子。模型的建立在Matlab 9.1軟件中實現。兩模型比較通過決定系數R2檢驗模型擬合優度，通過平均相對誤差MRE比較預測效果。

結 果

1.猩紅熱流行特征

研究數據為2011年1月至2018年12月底全國猩紅熱的月發病率。猩紅熱的流行情況在時間上具有明顯的季節規律，主要集中在每年的5～6月和11～12月，具體情況如圖2所示。

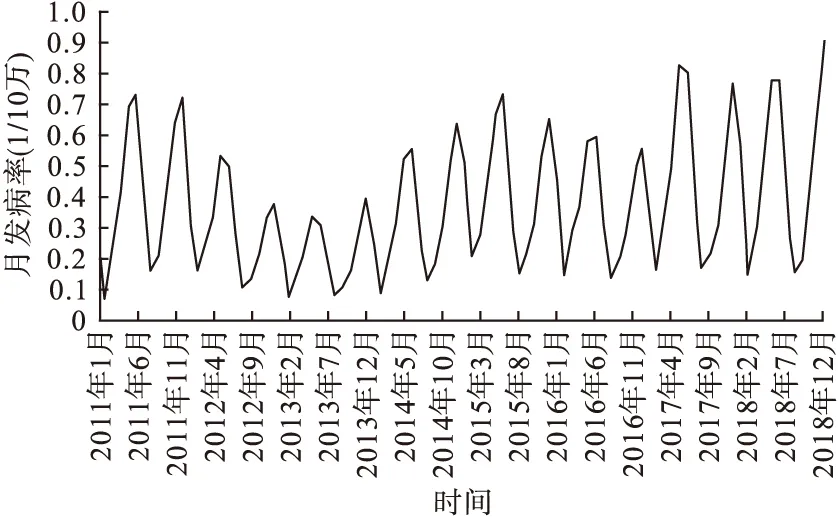
圖2 2011-2018年猩紅熱月發病率

2.ARIMA乘積季節模型建立

(1)模型識別

根據圖3中差分后序列均值圍繞零值波動，得出經過1階12步差分后序列滿足了平穩性，白噪聲檢驗顯示為非白噪聲序列(表1)，可以擬合ARIMA模型進一步提取信息。

表1 差分后序列的白噪聲檢驗

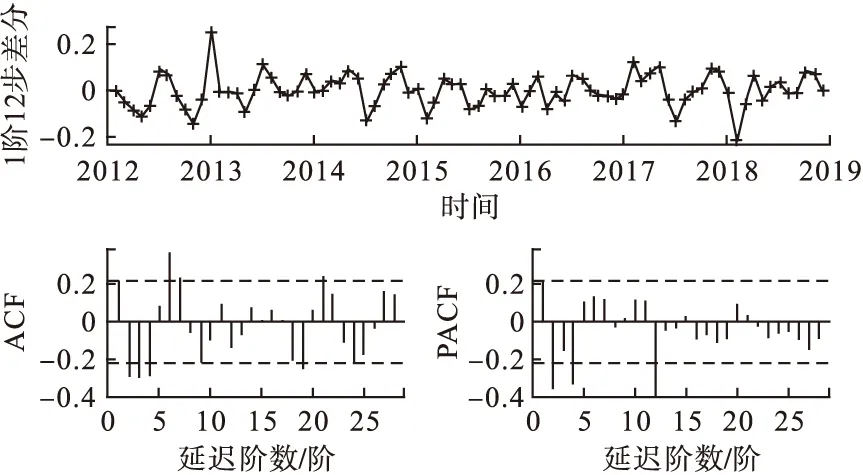
圖3 1階12步差分后序列的趨勢和相關分析

首先觀察差分后序列12階以內的ACF和PACF的特征，存在短期相關性；考察延遲12階的偏自相關系數，顯示序列存在著季節相關，可以考慮建立模型ARIMA(p，d，q)(P，D，Q)s，根據ACF和PACF的特征擬合短期相關模型ARIMA(2，2)提取短期相關信息；季節信息的提取根據相關資料可知，一般季節模型階數在2階以內，擬對P、Q分別取值0、1、2以確定最佳模型。經過反復調整，根據AIC最小的原則，初步擬合模型ARIMA(2，1，2)(0，1，1)12，詳見表2，圖3。

表2 ARIMA(p，d，q)(P，D，Q)12模型的選取

(2)參數估計與模型檢驗

ARIMA(2，1，2)(0，1，1)12模型的各參數估計值檢驗均有統計學意義，見表3。且模型順利通過了白噪聲檢驗，見表4。由圖4可知，擬合的模型的殘差ACF與PACF均落在的2倍標準差范圍之內，白噪聲檢驗均在0.05之上，可認為模型擬合有效，模型的平穩R2為0.336。據此確定擬合的模型為：

根據建立的模型預測2019年1～6月的猩紅熱發病率(1/10萬)的結果分別為0.637、0.274、0.377、0.579、0.910和0.937。

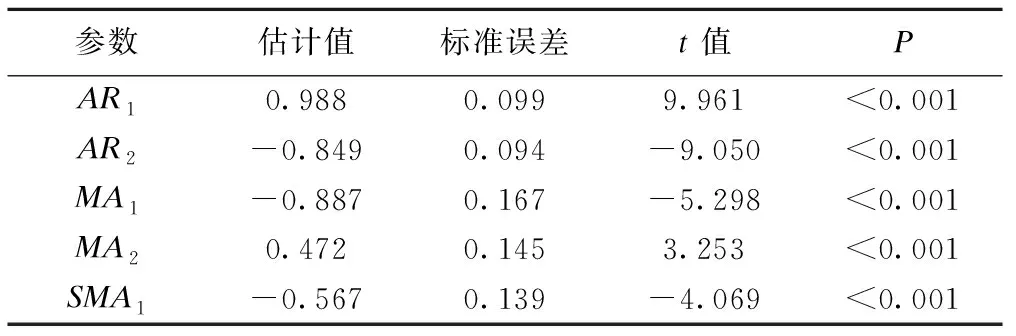
表3 ARIMA(2，1，2)(0，1，1)12模型參數估計

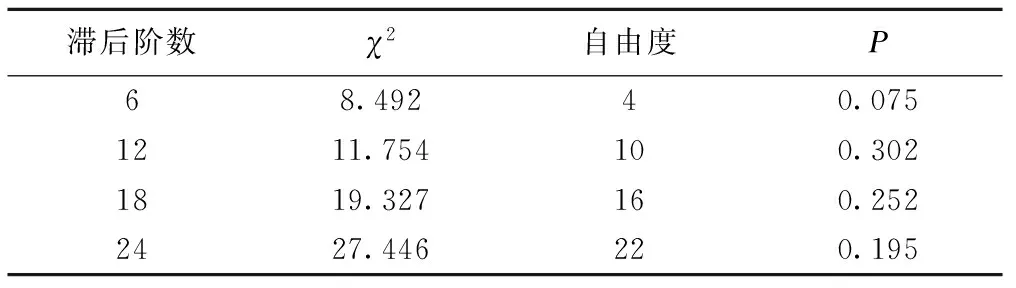
表4 ARIMA(2，1，2)(0，1，1)12模型殘差白噪聲檢驗

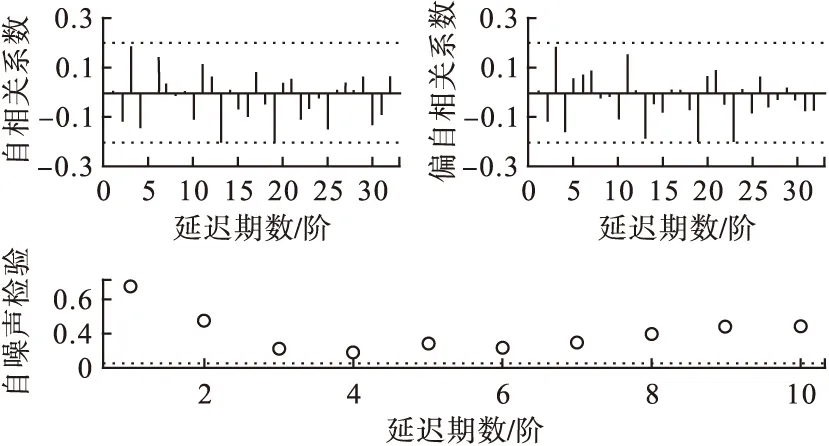
圖4 ARIMA(2，1，2)(0，1，1)12模型的殘差診斷

3.GRNN模型建立

本研究選擇的訓練集為2011年至2018年6月猩紅熱月發病率，測試集為2018年7～12月猩紅熱月發病率，模型的唯一參數spread由測試集最小均方誤差MSE對應的最優值確定?？梢妶D5，通過交叉驗證尋找最優光滑因子，即當spread=0.05時，MSE最小，對應的MSE為0.011，逼近能力強；此時模型的R2為0.823，擬合效果較好。根據建立的GRNN模型預測2019年1～6月發病率(1/10萬)分別為0.626、0.178、0.321、0.445、0.789和0.774。

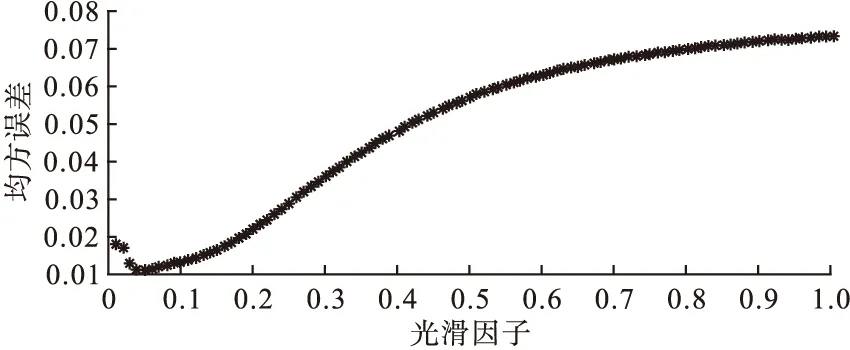
圖5 光滑因子對應的均方誤差曲線圖

4.猩紅熱預測能力比較

分別通過對2011-2017年6月數據進行訓練，預測2017年7～12月發病率；對2011-2017年數據進行訓練，預測2018年1～6月發病率；2011-2018年6月數據進行訓練，預測2018年7～12月發病率。兩模型的預測能力通過比較平均相對誤差大小，其中建立的三組GRNN模型的平均相對誤差分別為23.0%、21.3%、16.8%以及總的平均相對誤差為20.3%，三組ARIMA模型的平均相對誤差分別為47.5%、25.0%、20.8%以及總的平均相對誤差為31.1%，GRNN模型的平均相對誤差均小于ARIMA模型，認為預測能力較后者更優。詳見表5～7。

表5 ARIMA模型與GRNN模型第一次預測比較

表6 ARIMA模型與GRNN模型第二次預測比較

討 論

眾多研究表明ARIMA模型具有不受數據類型限制和較強適應性的優點，在短期預測中具有較好的表現能力[12-13]。ARIMA乘積季節模型可以提取出數據中蘊含的季節信息，當時間序列同時有短期相關性和季節趨勢時，需要擬合ARIMA季節乘積模型以分析數據中的短期相關性、季節效應與隨機誤差的復雜關系。ARIMA模型作為一種較為經典的方法在傳染病的預測上早已得到廣泛的應用，并且表現出短期預測精度較高的優點。

人工神經網絡能夠逼近任意的非線性關系，具有良好的泛化能力，此外，人工神經網絡沒有任何對變量的假設要求，許多國內學者已將該模型應用在對疾病的發病率研究當中。GRNN模型其局部逼近能力強，且學習速度較快，既解決了局部最優問題，又同時提高了訓練速度，且能保證預測的效果。

本研究結果顯示，兩種模型的預測結果與實際情況基本符合，均能較好地對全國猩紅熱發病率進行擬合。通過比較ARIMA乘積季節模型和GRNN模型的R2和預測結果的平均相對誤差，GRNN模型均優于ARIMA乘積季節模型，由于猩紅熱受到氣象因素、環境及個人防護等因素的影響，收集的資料數據是非線性的，而GRNN模型不對數據的分布做要求，故GRNN模型的預測能力更強，可以為今后研究猩紅熱等傳染性疾病的流行趨勢及提出防控措施提供科學依據。

本研究尚存在不足之處，GRNN訓練樣本的選取為猩紅熱的月發病率，神經網絡的學習程度和預測能力可能會受到一定影響，且猩紅熱與氣象因素密切相關，本研究未考慮氣象因素也可能影響預測精度，且傳染病流行規律復雜多變，在今后的研究中應及時更新數據對模型進行多次擬合，以提高預測水平。