基于OTSU改進的布匹檢測算法研究
解祥新,江小靜,劉琴琴,魏 燕
(南通理工學院,江蘇 南通 226002)
0 引言
基于閾值分割的布匹疵點檢測算法可以大致分為以下幾個步驟,首先對采集到的布匹圖像進行降噪,消除無關信息,增強細節對比度等[1],再利用閾值分割算法進行圖像分割,最后將得到的分割后的圖像進行疵點分類等后續處理。在實際生產中,疵點類型主要以破洞、斷經為主[2],因此本文中所檢測的疵點類型基本為破洞、斷經。
1 改進最大類間方差法
OTSU全稱最大類間方差法,該方法將待檢測樣本的前景和背景分離開來。本文將素色布匹的正常底紋看作背景,把待檢測素色布匹的瑕疵區域看作前景。通過OTSU閾值分割算法把素色布匹瑕疵區域和標準紋理背景信息進行解耦[3],得出的最佳閾值將布匹瑕疵與紋理背景分割開來,實現瑕疵檢測。
最大類間方差算法具有檢測周期短和運算速度快等優點[4],可以滿足工業現場的實時檢測要求。
傳統最大類間方差算法原理:假定待檢測的素色布匹圖像共有L個灰度級,nq是灰度級為q的像素點個數,則圖像灰度級的概率Pq如下式:
(1)
K級灰度以下像素的灰度概率均值和累積值分別是ωk和μk,如式(2)和式(4)所示:
(2)
ω(L-1)=1
(3)
(4)
假設按照灰度閾值T把待檢測素色布匹樣本圖像分為布匹正常底紋和表面瑕疵區域兩類:C0類(灰度級為從0到T),C1類(灰度級為從T+1到L-1)。則C0類和C1類兩類的概率公式為式(5)和式(6)所示:
(5)
(6)
兩類的均值可以用式(7)和式(8)表示:
(7)
(8)
對于整個圖像來說,其灰度均值為式(9):
μ=μ0ω0+μ1ω1
(9)
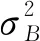
(10)
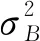
傳統的最大類間方差法的缺點:
(1)對于一些灰度級不連續的圖像來說,通過傳統的最大類間方法所計算出來的閾值很難收斂到全局最優。
(2)若背景圖像與前景圖像分布差異非常大,那么最大類間方差算法將有可能會失效。
(3)當圖像中僅有兩種類別時,最大類間方差能夠很好地適用;但是當超過兩種類別時,就需要改進增加額外閾值,來進行分割。
因此針對以上傳統最大類間方差法的缺點進行如下改進:
(1)計算圖像灰度級L。計算圖像的灰度平均值μT,將μT取整|μT|作為圖像的灰度級,即L=|μT|;
(2)給分割次數賦以初始值J=1;
(3)利用最大類間方差法計算圖像的像素N、閾值K、閾值選擇函數η、類內方差σw;
迭代,N(J)=N;K(J)=K;L=K;η(J)=η;σ(J)=σw;J=J+1;
(4)如果J≤1,那么返回步驟3;若大于1,則計算出ε的值。
(11)
(5)如果ε≥0,那么返回步驟3;若小于0,則查找最大η(J)所對應的閾值,作為最佳閾值K。
2 實驗步驟及仿真
本節算法的流程如圖1所示。

圖1 基于改進最大類間方差法的檢測算法流程
具體步驟如下:
步驟1:采集現場布匹圖像,進行雙邊濾波處理,經過雙邊濾波處理之后能夠較好的濾除低頻信息,減少低頻信息的干擾,并且能夠很好地保存圖像邊緣處的細節信息。雙邊濾波的數學表達式如下:
(12)
其中,(k,l)為模板窗口的中心坐標;(i,j)為模板窗口的其他系數的坐標;σd為高斯函數的標準差。
步驟2:將雙邊濾波處理后的圖像再通過中值濾波濾除斑點噪聲及椒鹽噪聲,中值濾波在降噪的同時也能夠有效保存邊緣處的細節。用中值濾波處理雙邊濾波處理后的圖像g(i,j):
G(x,y)=mid{g(x-a,y-b),a,b∈W}
(13)
其中,G(x,y)為進行中值濾波后的二階矩陣,W為選擇的二維模板,選取3×3的區域;
步驟3:將預處理后的圖像,利用改進的最大類間方差法進行閾值分割。計算圖像灰度級L,計算圖像的灰度平均值μT,令L=|μT|;給分割次數賦以初始值J=1;利用最大類間方差法計算圖像的像素N、閾值K、閾值選擇函數η、類內方差σw;再進行迭代,直到計算出最佳閾值K。
步驟4:分割完成后判斷是否存在疵點,如果不存在疵點,則繼續采集圖像進行疵點檢測;若存在疵點,則進行邊緣檢測,標識出疵點,進行數據保存后,再繼續采集圖像。
傳統最大類間方差法在閾值分割時,并不能很好地將疵點分割出來,而通過改進的最大類間方差法,能夠很好地分割出疵點。傳統最大類間方差法檢測準確率只有78%,而改進后的最大類間方差法檢測準確率可達到94%。
3 結語
本文主要研究基于改進最大類間方差法的檢測算法。并通過實驗仿真分析這種算法在針對無樣本的疵點檢測上精度高,具有一定的效果。

