三余弦公式在求解空間角問題中的應(yīng)用

◇ 浙江 沈新權(quán)(正高級教師)

異面直線所成的角、斜線與平面所成的角以及二面角等概念,構(gòu)成了比較完整的空間角的概念.學(xué)習(xí)這些概念并掌握這類問題的求解方法對于學(xué)生建立空間觀念,提高對空間位置關(guān)系的認(rèn)識,發(fā)展邏輯推理、直觀想象、數(shù)學(xué)運(yùn)算等學(xué)科核心素養(yǎng),起著十分重要的作用.由于三余弦公式聯(lián)系了線線角和線面角,因此利用三余弦公式在處理和解決一些空間角的問題時有著獨(dú)特的功效.

1 三余弦公式

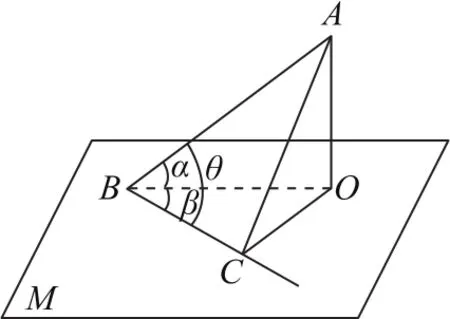
圖1

公式如圖1所示,若斜線AB與平面M所成角為α,平面M內(nèi)的一條直線BC與這條斜線AB及AB的射影BO所成的銳角分別為θ,β,則有cosθ＝cosα·cosβ(三余弦公式).

證明過點O作OC⊥BC于C,連接AC,則AC⊥BC.在Rt△AOB中在所以有cosθ＝cosα·cosβ,結(jié)論成立.

說明(1)公式特征:兩個互相垂直的平面內(nèi)(AOB-C)的兩條直線(BA與BC)所成角的余弦等于這兩條直線與另一個平面所成角(∠OBA與∠OBC,即這兩條直線與交線(OB)所成的銳角)的余弦的乘積.

(2)因為θ,α,β均為銳角,且cosθ＝cosα·cosβ≤cosα,所以θ≥α,由此可知,一條斜線與已知平面中的任一條直線所成的角中,線面角最小,此即為最小角定理.

2 利用三余弦公式處理和求解空間角

1)比較空間角的大小

例1(2019年浙江卷8,節(jié)選)設(shè)三棱錐V-ABC的底面是正三角形,側(cè)棱長均相等,P是棱VA上的點(不含端點),記直線PB與直線AC所成角為α,直線PB與平面ABC 所成角為β,則( ).

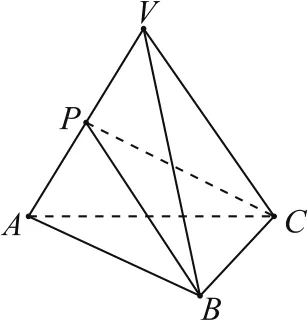
圖2

A.α＝β B.α＞β

C.α＜β D.不能確定

分析由于點P是動點,所以直線PB也是動直線,如果直接求α與β的值,再去比較它們的大小,會比較麻煩.但我們注意到β為PB與平面ABC所成的角,而AC在平面ABC內(nèi),因此,利用最小角定理即可得到結(jié)論.

解由于直線AC在平面ABC內(nèi),且PB與平面ABC所成角為β,由最小角定理知α＞β,選B.

2)處理線線角

例2如圖3,已知點P在正方體ABCD-A′B′C′D′的對角線BD′上,∠PDA＝60°.求DP與CC′所成角的大小.

分析因為平面BDD′B′與平面ABCD垂直,且它們的交線為BD,所以由∠PDA＝60°,∠ADB＝45°,利用三余弦公式可求得∠BDP,而DP與CC′所成角與∠BDP互余,問題得以解決.

解設(shè)DP與CC′所成的角為θ,因為CC′∥DD′,則 ∠D′DP＝θ.因 為 平 面 BDD′B′與 平 面ABCD垂直,由三余弦公式得

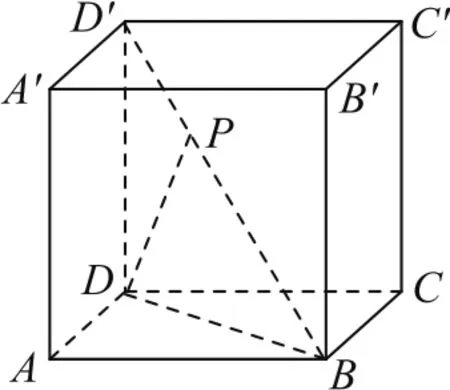
圖3

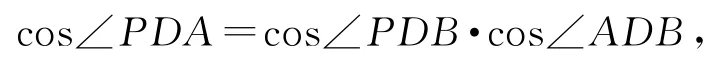
所以

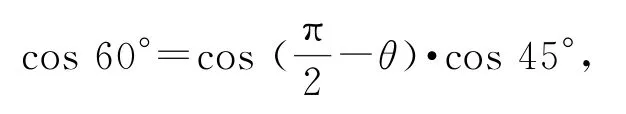
例3(2017年全國卷Ⅲ理16)a,b為空間中兩條互相垂直的直線,等腰直角△ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉(zhuǎn)軸旋轉(zhuǎn),有下列結(jié)論:

① 當(dāng)直線AB與a成60°角時,AB與b成30°角;

② 當(dāng)直線AB與a成60°角時,AB與b成60°角;

③ 直線AB與a所成角的最小值為45°;

④ 直線AB與a所成角的最小值為60°.

其中正確的是______(填寫所有正確結(jié)論的編號).

分析這是一個動態(tài)的問題,從條件來看,建立空間直角坐標(biāo)系,然后利用向量法就可以判斷結(jié)論是否正確.但作為一個填空題,如此“大動干戈”,似乎“小題大做”了.我們先根據(jù)題意,畫出圖形.如圖4所示,設(shè)CD為直線a,CE為直線b,過B分別作a,b的平行線BM,BN,則直線AB與直線a,b所成的角分別為∠ABM＝α,∠ABN＝β.注意到,當(dāng)斜邊AB以直線AC為旋轉(zhuǎn)軸旋轉(zhuǎn)時,平面ABC始終與a,b所確定的平面是垂直的,設(shè)∠CBM＝θ,由題意可知∠CBN＝90°－θ.由三余弦公式可以得到α,β與θ的關(guān)系,然后進(jìn)行判斷.

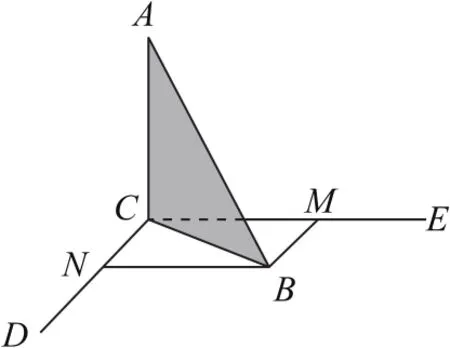
圖4

解根據(jù)三余弦公式,有cosα＝cos∠ABM＝同理,有cosβ＝由此可以判斷命題②③正確.

3)求解線面角

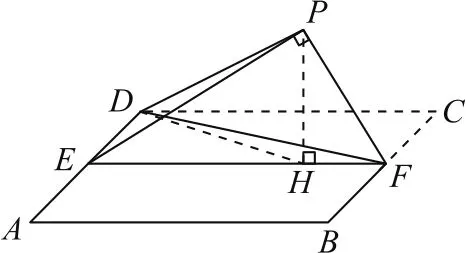
圖5

例4(2018年全國卷Ⅰ理18)如圖5所示,四邊形ABCD為正方形,E,F分別為AD,BC的中點,以DF為折痕把△DFC折起,使點C到達(dá)點P的位置,且PF⊥BF.

(1)證明:平面PEF⊥平面ABFD;

(2)求DP與平面ABFD所成角的正弦值.

分析在解決問題(2)時,因為平面PEF⊥平面ABFD,所以過點P作PH⊥EF于H,則PH⊥平面ABFD,因此有平面PDH⊥平面ABFD,連接DH,則有 cos∠PDE＝cos∠PDH·cos∠EDH,而∠PDH為DP與平面ABFD所成的角.

解(1)由已知可得,BF⊥PF,BF⊥EF,且PF,EF?平面PEF,PE∩EF于E,所以BF⊥平面PEF.又BF?平面ABFD,所以平面PEF⊥平面ABFD.

(2)作PH⊥EF,垂足為H,由(1)知,PH⊥平面ABFD,DE⊥PE,不妨設(shè)DP＝2,則DE＝1,從而又PF＝1,EF＝2,所以PE⊥PF,于是,所以斜線角為∠PDE＝60°,因為,設(shè)DP與平面ABCD所成角為α,則由三余弦公式知cosα·cos∠EDH＝cos60°,從而.

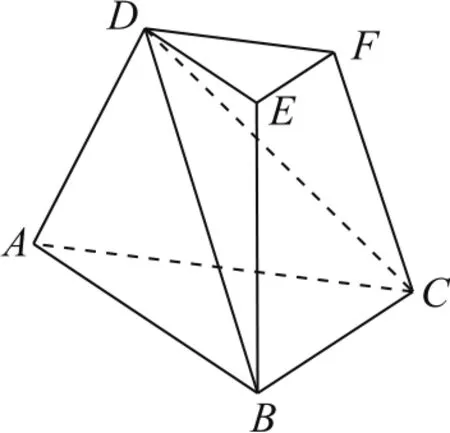
圖6

例5(2020年浙江卷19)如圖6所示,在三棱臺ABC-DEF中,平面ACFD⊥平面ABC,∠ACB＝∠ACD＝45°,DC＝2BC.

(1)證明:EF⊥DB;

(2)求直線DF與平面DBC所成角的正弦值.

分析(1)因為EF∥BC,所以要證明EF⊥DB,只需證明BC⊥BD.由于平面ACFD⊥平面ABC,且CD,CB分別在平面ACFD與平面ABC內(nèi),因此由三余弦公式有cos∠BCD＝cos∠ACB·cos∠ACD.

(2)過點D作DO⊥AC于O,因為DF∥OC,所以DF與平面DBC所成角為OC與平面DBC所成角.由∠ACB＝∠ACD＝45°,得點O在平面DBC上的射影G在∠DCB的角平分線上.在直二面角D-CG-O中,由三余弦公式可得cos∠OCD＝cos∠OCG·cos∠DCG,從而可以求出OC與平面DBC所成角即DF與平面DBC所成角的余弦(正弦)值.

解(1)如圖7所示,因為平面ACFD⊥平面ABC,所以過D作DO⊥AC于O,連BO,則DO⊥平面ABC.由三余弦公式cos∠BCD＝cos∠ACB·cos∠ACD,由∠ACB＝ ∠ACD＝45°,得因為DC＝2BC,所以BC⊥BD.因為EF∥BC,所以EF⊥DB.

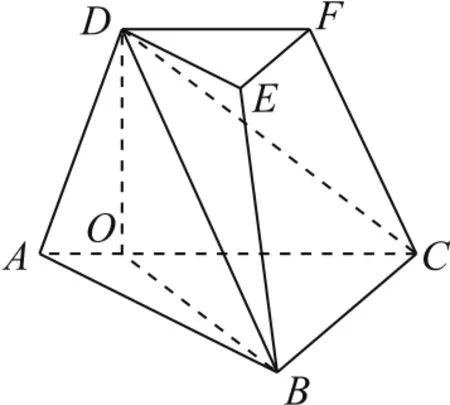
圖7

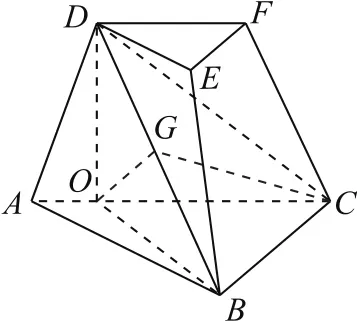
圖8

(2)如圖8所示,過點D作DO⊥AC 于O,因為∠ACB＝∠ACD＝45°,所以點O在平面DBC上的射影G一定在∠DCB的平分線上.設(shè)直線DF與平面DBC所成角為θ,因為OC∥DF,所以O(shè)C與平面DBC所成角也為θ.由(1)知由三余弦定理知cos∠OCD＝cosθ·cos∠DCG,即從而sinθ＝,即直線DF與平面DBC所成角的正弦值為.

3 判斷直線與平面所成角的條數(shù)

例6已知二面角α-l-β的大小為50°,P為空間中任意一點,則過點P且與平面α和平面β所成的角都是25°的直線的條數(shù)為( ).

A.2 B.3 C.4 D.5

分析過點P作平面α,β的垂線,垂足分別為A,B,則PA,PB所成的角為50°或130°,設(shè)過點P且與平面α和平面β所成的角都是25°的直線為m,則m與PA,PB所成的角都為65°.接下來,我們探究m與PA,PB所成的角都為65°的直線條數(shù).

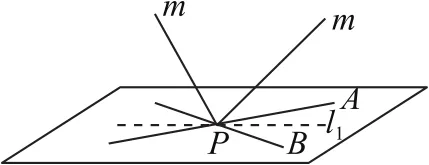
圖9

解先假設(shè)m與PA,PB所成的角都為θ,則直線m上任意一點在PA,PB所確定的平面上的射影一定在PA,PB的角平分線上.由前面的分析我們知道PA,PB的角平分線l1,l2與PA,PB所成的角分別為25°與65°,設(shè)直線m與PA,PB所在平面所成的角為φ,由三余弦公式有cosθ＝cos25°·cosφ或cosθ＝cos65°·cosφ,由cosθ＝cos25°·cosφ≤cos25°,得θ≥25°,即以直線l1為射影的直線m與PA,PB所成的角都為θ的最小值為25°,因此m與PA,PB所成的角都為65°的直線有2條.如圖9,由cosθ＝cos65°·cosφ≤cos65°,得θ≥65°,此時以直線l2為射影的直線m與PA,PB所成的角都為65°的直線有1條(與PA,PB所成的角為130°的角的角平分線),從而過點P且與平面α和平面β所成的角都是25°的直線的條數(shù)為3條.故選B.

4 三余弦公式的推廣

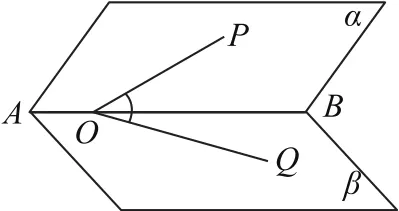
圖10

如圖10所示,二面角α-AB-β的大小為φ,O為AB上任意一點,OP,OQ分別在平面α,β內(nèi),∠POB,∠QOB,∠POQ分別為α,β,θ,則cosθ＝cosα·cosβ＋sinα·sinβ·cosφ.有的書稱此結(jié)論為三射線公式.當(dāng)φ＝90°,即二面角α-AB-β為直二面角時的三射線公式就是三余弦公式.利用三射線公式在求解二面角的大小時非常方便,有興趣的讀者可以自行完成三射線公式的證明并探究它的應(yīng)用.