聚類問題中的算法

李曉明

本專欄上一期介紹的是分類問題中的算法，這一期討論聚類。

“分類”指的是要將一個未知類別的對象歸到某個已知類別中。“聚類”則是要將若干對象劃分成幾組，稱每一組為一個類別。

在實際應用中，分類的類別是事先給定的，往往對應某種現實含義，如網購者可能分為“隨性”和“理性”兩個類別，人們大致也知道是什么意思。聚類則是本無類，只是根據對象之間的某種相似性（也稱鄰近程度或距離），將它們分組。例如，有兩個任務要完成，于是需要將一群人分成兩組，分別去完成一個任務，為了有較高的效率，希望組內成員之間關系較好，配合默契。聚類形成的類不一定有明顯的外在特征，往往只是根據事先給定的目標類數（如有三個任務，就要分成三組），將對象集合進行合理劃分。

所謂“合理”，在這里的原則就是盡量讓同組的成員之間比較相似（距離較近），組間的成員之間距離較遠（不相似）。一旦分類完成后，就可能會按照不同類的某些特征給它們分別命名。

與分類一樣，為了聚類，對象之間的相似性（或距離）含義和定義是基礎。在有些應用中，對象兩兩之間的相似性是直接給出的;在更多的應用中，相似性則要根據對象的特征屬性按照一定的規則進行計算。下面我們討論兩個算法。

● 自底向上的分層聚類法

想象我們要搞城市群建設，需要規劃將一些城市分成幾個群，群內統籌協調發展。一共要分成幾個群？哪些城市該放在同一個群里？這是很現實的問題。當然，做出這樣的決定取決于許多因素，但其中一個重要因素就是城市間的空間距離。很難想象同一個群內的城市之間相距很遠，而相距很近的兩個城市卻分到了不同群。

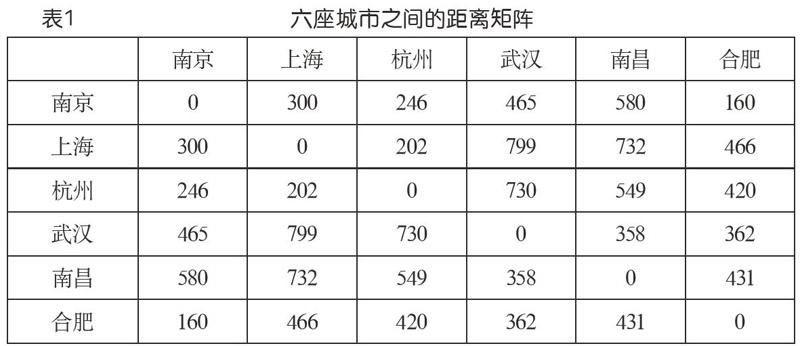
表1是六座城市之間的距離矩陣（在搜索引擎中查出來的數據，不一定很準，這里只是作為例子），如果我們想分成兩個群，該如何分？分成三個呢？這就是聚類問題。我們注意到，在這種背景下，兩個對象（城市）之間的相似性或鄰近程度自然地以距離的方式給了出來。

1967年，Stephen Johnson發表了一個針對這種場景的算法，稱為“分層聚類法”（hierarchical clustering）。基本思想如下（假設有n個對象，要聚成k類）：

（1）初始，每一個對象看成是一個類，于是有n個類，類和類之間的距離由表1那樣的矩陣數據給出。

（2）兩兩檢查現有類之間的距離，挑出最小的，也就是表1數據中最小的（不算對角線元素，因為它們是“自己到自己”的距離）。將對應的兩個類合并，具體就是將它們的數據“合并到”一行（列）上，刪去另一行（列）。數據合并的策略有多種考量，其中一種是取對應兩個數的較大值。（注意，現在類數少了一個，對應表1那種矩陣少了一行一列）

（3）如果已經是k類了，就結束;否則返回（2）。

我們以表1為例，初始6個類，考慮k=3，也就是要聚為3類，來模擬算法的運行。核心是算法的第（2）步。由于數據矩陣的對稱性，觀察的時候只需考慮上三角。為簡單清楚起見，更新的時候則統一處理。

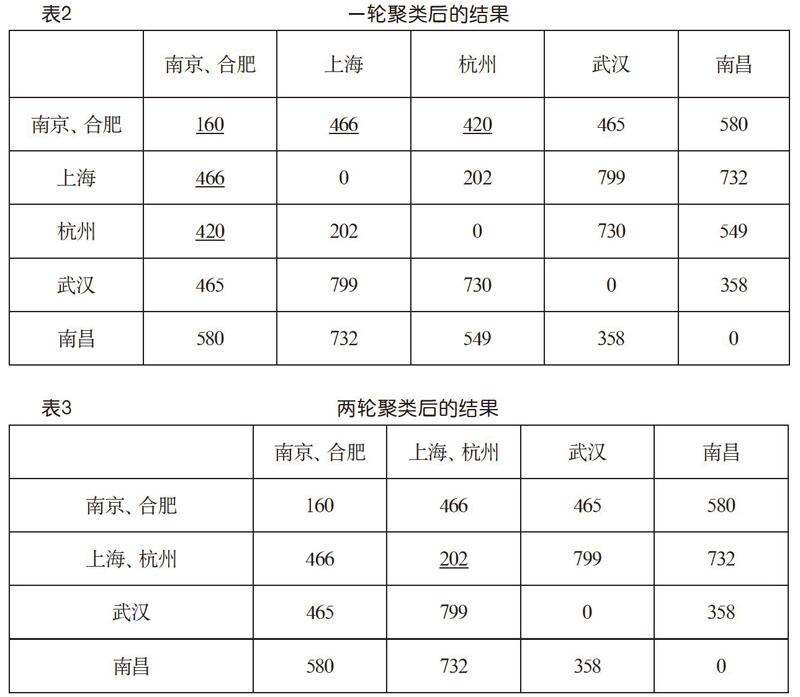
首先，看到表1上三角中最小的數是160，即南京和合肥之間的距離。它位于第1行第6列。按照算法，應該將南京與合肥聚成一類，同時合并它們的數據，對應矩陣數據的更新。我們取較大值方案，并讓第6行（列）向第1行（列）合并，就得到表2所示的結果。發生了更新的數據由下畫線標示。現在是5個類，比初始減少了一個。其中加下畫線顯示的數就是取較大值更新的結果。

繼續，看到最小的數是202，上海與杭州之間的距離，位于第2行第3列。將它們合并為一類，并讓第3行（列）向第2行（列）合并，就得到表3所示的結果。這一次，除了對角線上的數據外，第2行的其他數據恰好沒有變化。現在就是4類了。

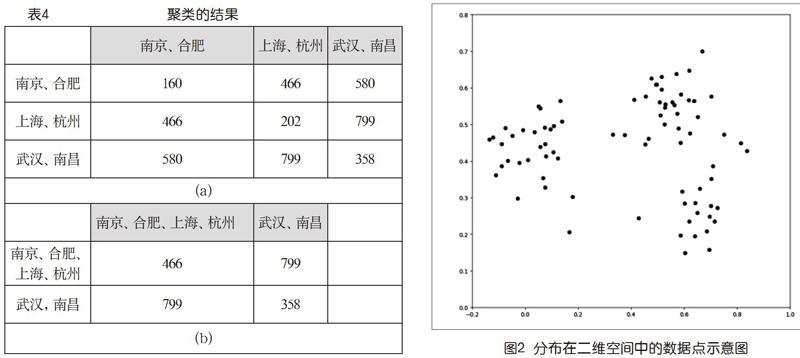
再來一輪，看到第3行第4列的358最小，讓第4行（列）向第3行（列）合并，就得到下頁表4（a）所示的結果。這就是聚成3類了，達到了預定目標。

若需要，還可以在這個基礎上繼續，得到聚為2類的結果如下頁表4（b）所示。

如果能把這個例子跟蹤下來，相信讀者一定就掌握了這個算法的要領。

這個算法的聚類效果如何？看這個例子，似乎還不錯。但要意識到，像許多機器學習算法一樣，效果沒有一個“金標準”度量，而是與數據集和應用目的有關。因而，這類算法常常包含一些啟發式，用以根據具體情況斟酌采用。對S.C. Johnson算法而言，啟發式的體現就在于算法第（2）步中的數據合并策略。我們例子中用的是“較大值”，其他策略還有“較小值”“平均值”等。建議讀者思考體會這幾種策略的“物理意義”，從而在應用中可以有針對性地選用。

這個算法的時間效率如何？如果任務是要把n個對象聚成k類，每一輪找到最小的數是主要操作，總起來就是O（（n-k）*n2）。

● K-means

下面討論另一個聚類算法——K-means（K均值）算法，也是現在大數據聚類中比較流行的算法，其中的K是預先給定的要形成的類數。作為一個例子，考慮有若干數據點（不妨認為它們代表一些人的年齡），并將其放到數軸上，如下頁圖1所示。

設想要把它們分成4組，每一組內的人的年齡比較相近，以便談話更有共同語言。怎么分合適呢？就這個例子而言，乍一看這個圖，可能還真有點為難。頭3個為一組，接著7個為一組，再接著6個為一組，后面4個為一組？還真不見得。

這個例子數據，每個數據點就一個值，稱之為1維數據。而在實際中常見的是多維數據。例如，圖2是一個二維數據點集的情形。如果要把它們聚成2類，似乎有很直觀的結果，3類也行，4類就不太好說了。讀者還可以想到，如果數據的維數>2，情況會變得更加復雜①，而且不太可能有視覺直觀。

無論數據的維度如何，如前所述，數據之間的距離都是聚類算法的基礎。在前面討論分層聚類法的例子中，我們直接用城市間的空間距離作為距離。在本專欄上一期討論分類的時候，我們談到了不同的應用背景有不同的距離、如歐式距離、曼哈頓距離，余弦距離等，此處不再贅述。

下面以二維為例進行算法討論，其思想也可以用于多維。后面的運行例為簡單起見，則采用上面的年齡數據（一維）。

1.問題

給定一個二維數據集合D={x，y，…}和希望聚成的類別數K，要將那些數據分成K組，使得每一組內的數據點較近，而組間數據點的距離較遠。假設采用歐式距離。

稍為仔細一點讀這個問題描述，會感到它只是表達了一個宏觀的愿望，細節要求并沒有說清楚。“較近”和“較遠”的具體比較對象是什么呢？以圖2為例，若聚成3類，無論怎么聚，不同類邊界上兩個點的距離都有可能比類中兩個點的距離更近。那豈不是說這個問題沒法解決？

為此，我們需要讓那種宏觀的愿望具有可操作性，明確“類中數據點較近”和“類間數據點較遠”的具體含義。注意到由于有了距離的概念，我們就可以談論一組數據的“中心”，如一維空間中兩個數的中心就是它們的均值，二維空間中兩個數據點的中心就是它們連線的中點，等等。而如果有多個中心，就可以談論一個數據點離哪一個更近。K-means就是從初始給定的數據點集合出發，對K個不同中心的確定和數據點歸屬關系進行迭代，最終形成K個數據類別的算法。

2.算法思路

在K-means算法中，K表示類別數，means表示均值。意指聚類過程將數據集分成了K類，每一類中的數據點都離它們的中心（亦稱質心）更近，離其他的中心較遠。

“中心”，在本文的討論中就是一個虛擬的數據點，其坐標為它所代表的數據集中數據點坐標的平均值。如果是兩個點，如x=（1，2），y=（4，6），其中心就是（（1+4）/2，（2+6）/2）=（2.5，4）;如果是三個點，如x=（1，2），y=（4，6），z=（4，4），其中心就是（（1+4+4）/3，（2+6+4）/3） =（3，4）;等等。一般地，n個點，d1=（x1，y1），…，dn=（xn，yn），中心就是：

K-means算法，就是基于待聚類的數據，迭代尋找中心的過程。它根據預設的類別數K，為每個類別設定一個初始中心（可以隨機產生），然后按照離它們距離的遠近，將數據做歸屬劃分。一旦有了數據劃分，反過來就可以計算它們的中心，然后再按數據離新中心的遠近對數據做重新劃分。如此反復，直到中心不再改變。屆時，就達到了每個數據點都離所在類的中心最近的目標。

3.算法描述（如圖3）

4.算法運行例

二維數據作為手工呈現的例子會比較煩瑣。我們不妨利用前面的一維年齡數據例子，體會一下過程。

5，10，13，21，23，24，25，39，41，42，52，55，58，59，61，62，72，79，82，92

根據題意，K=4，隨機設初始中心為10，30，50，70。注意，它們不需要屬于初始數據點集。

以距離最近為原則，將20個數據點做第一次劃分，如表5（a）所示，而根據劃分得到的新中心如表5（b）所示。

然后以這些中心為參照，將所有數據按離新中心的距離重新劃分（看到先前第4類中有些數據跑到第3類了），得到新的4個類別：{5，10，13}，{21，23，24，25，39}，{41，42，52，55，58，59，61，62}，{72，79，82，92}。

再計算中心，前兩個不變，第3個成為（41+42+52+55+58+59+61+62）/8=53.75，第4個變成（72+79+82+92）/4=81.25。按它們再劃分數據，發現沒有引起變化，K-means聚類過程完成！我們清楚地看到了中心的確定和類別劃分之間的相互“迭代”。上述過程也可以用下頁表6來表示。

5.算法分析

K-means算法是經典的聚類算法，上一輪的結果作為新一輪計算的開始值，直至前后兩輪計算的結果落在一個誤差范圍中，即趨于穩定。這里要關心的基本問題就是它是否能趨于穩定，也就是其中|new_centers-centers|是否能變得小于一個任意設定的門檻值threshold，即“收斂”。否則，這算法就會無窮無盡地執行下去。數學理論告訴我們，收斂會發生。盡管我們不需要懂得證明，但懂得這是需要關心的事情是算法素養的要求。

也許我們覺得還應該從收斂時聚類結果是否合理來討論正確性，也就是“到底聚對沒有”？但這通常會比較主觀，與應用背景有關。以上述一維數據為例，如果將它們看成是年齡，我們腦子里事先已經有了少年、青年、中年、老年這樣幾個背景概念，也許你會覺得若41和42在第2類會更加合理。但如果那些數據有不同的含義，就不一定了。由于算法是不理解數據的含義的，它只負責類中心的收斂（數學上嚴格的，也符合實際中關于聚類的一些直覺）。在這個意義上，它就是正確的。至于它在某個具體問題上是否合適，則需要在特定應用背景下的實踐來檢驗了。不過，取決于初值的選取，盡管都會收斂，但結果類中心不是唯一的，可能造成數據集劃分的不同。這也需要在實際應用中注意。

從執行效率看，算法是一個兩重循環。內層循環就是對數據集的兩次遍歷，一次做劃分（在K個類中心中選取最近的），一次計算新的中心。外層循環執行的次數與類中心初值的選取有關。假設N為樣本數據量，K為類別數，M為外層循環的迭代次數，算法復雜性就是O（M*N*K）。

由上述討論可見，K-means算法的時間開銷除了與數據樣本數、聚類的類別數有關外，初始聚類中心的選擇對聚類結果也有較大的影響，一旦初始值選擇得不好，不僅會影響收斂速度，而且可能無法得到有意義的聚類結果。由此可見，聚類算法的效率和質量不僅僅是計算機算法的問題，對要解決的問題本身的了解和經驗也是重要的因素。

當然，當我們對要處理的問題不夠了解時，可以用隨機數作為初始中心，還可以用不同的類別數對同一數據集合做多次嘗試，與熟悉應用背景的專業人士合作，解讀、解釋有關數據，最終確定合適的類別數，預設中心的初始值。

釋： ①所謂“維數”，指的是數據對象特征的個數。在人工智能應用中，維數可能達到成千上萬。

參考文獻：

[1]S.C.Johnson.Hierarchical Clustering Schemes[J].Psychometrika，1967（02）：241-254.

[2]Anil K. Jain.Data clustering：50 years beyond K-means[J].Pattern Recognition Letters，2009.

注：作者系北京大學計算機系原系主任。